Long Short Term Memory (LSTM)

태그
Recurrent Neural Network
포스팅 날짜
2021/09/12
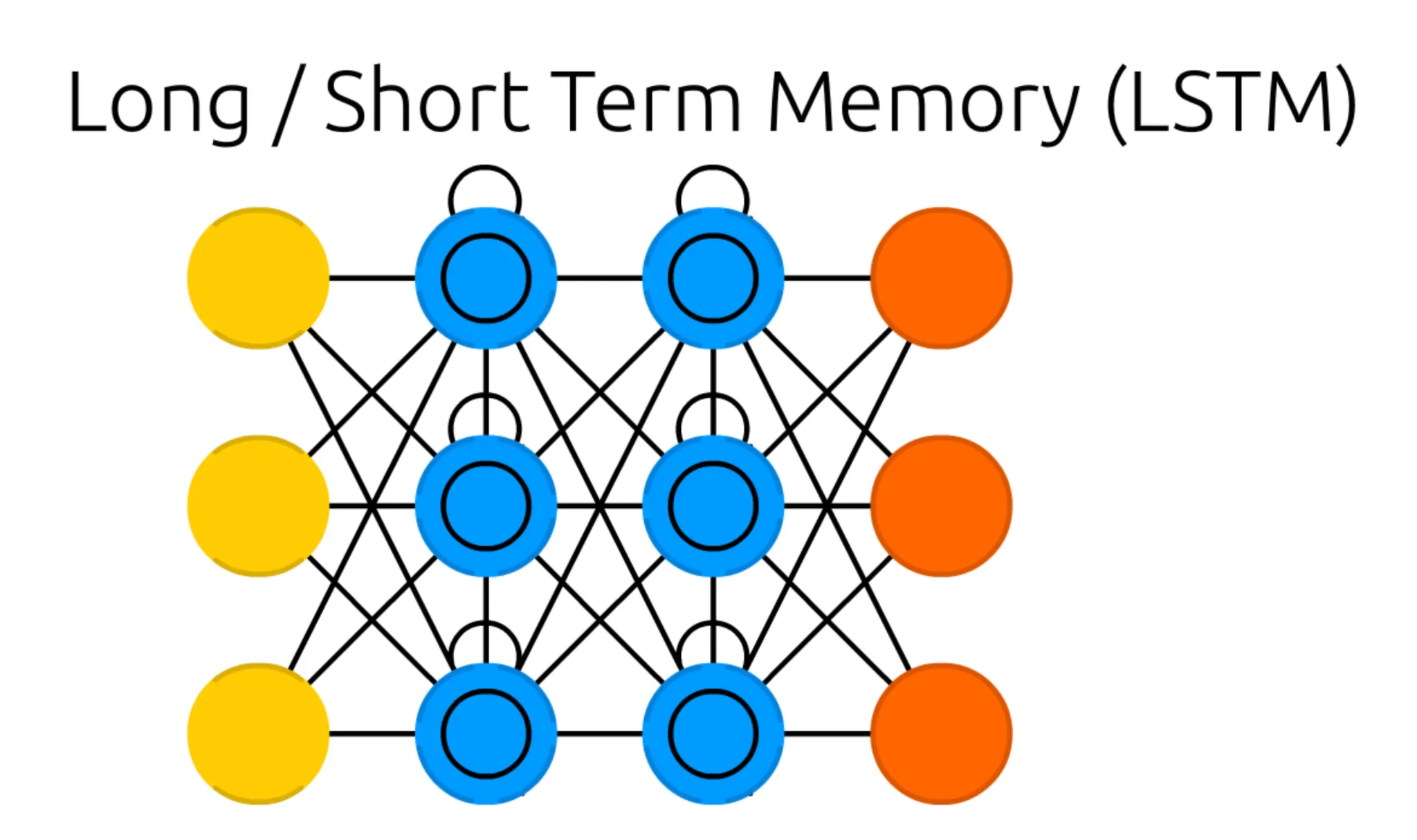
본 세션에서는, RNN 을 기본으로 하여 설계된 ANN 이자, 마찬가지로 Recurrent Cell 이 존재하는 네트워크인 Long Short Term Memory(LSTM) 에 대해서 알아보려고 합니다.
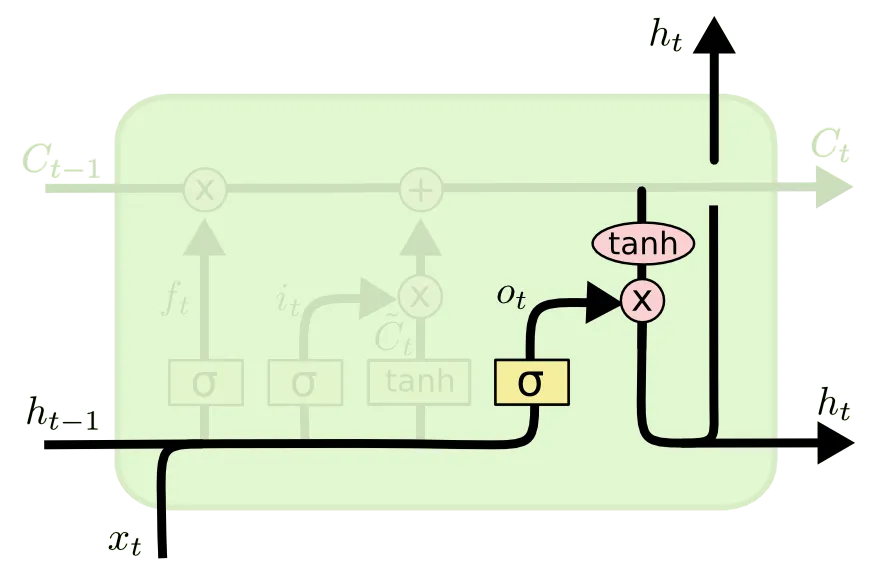
가장 먼저 보이는 구조의 특징적인 변화는 Recurrent Cell 이 있던 위치에, 내부에 동심원이 그려진 다른 Cell 이 존재한다는 점입니다. 이러한 형태의 Cell 을 Memory Cell 이라고 합니다. 이전 RNN 때와 마찬가지로, Input Cell 과 Output Cell 및 Memory Cell 의 개수는 구조와 관련이 없다는 점 알아주시면 좋을 것 같습니다.
그렇다면 잘만 쓰고 있던 Recurrent Cell 을 버리고 Memory Cell 이 갑자기 왜 필요했을까요?
그 이유는 Recurrent Neural Network 의 고질적인 Gradient Vanishing Problem 에서부터 이어집니다.
Gradient Vanishing Problem 은 딥러닝 분야에서 굉장히 유명한 문제점입니다. 간단하게 설명드리자면, Backward Propagation 을 진행할 때, gradient 값이 소실되는 문제점입니다.
이렇게만 설명드리면 읭...? 하실 분들을 위해서 Backward Propagation 에서 gradient 가 소실되는 이유에 대해서 설명드리려고 합니다.
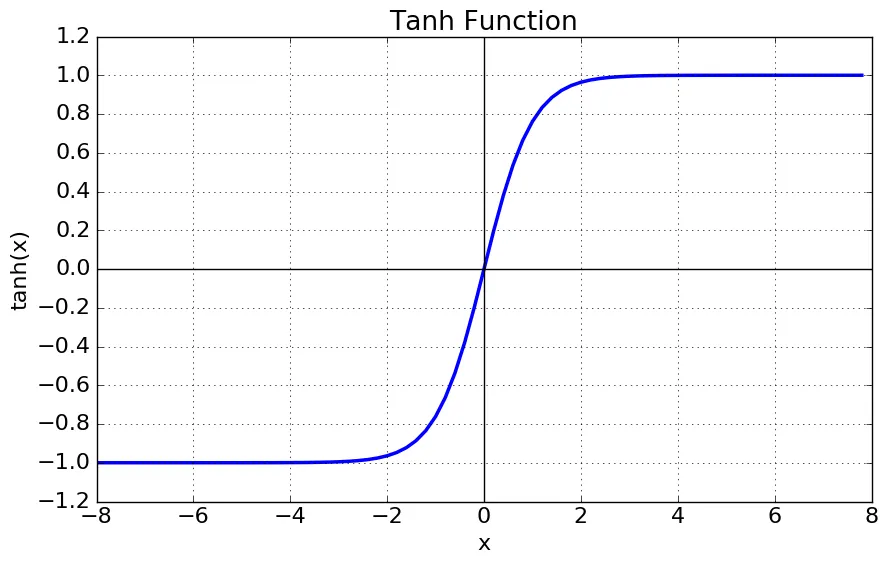
RNN 을 비롯한 딥러닝 네트워크에서는 activation function 을 사용합니다. 그 중에서도 RNN 에서는 지난 시간에 tanh⁡\tanh 를 사용한다고 말씀드린 적 있습니다.
여기서, Back Propagation 의 기본 원리에 대해서 알 필요가 있습니다. Back Propagation 은 upstream gradient 와 local gradient, 그리고 chain rule 을 사용해 downstream gradient 를 계산해내는 과정으로 보시면 됩니다.
이 때, local gradient 는 특정 연산의, 특정 input 에서의 미분값입니다. tanh⁡\tanh 도 엄밀하게 네트워크의 연산 중 하나이며, backward propagation 을 진행할 때 지나가야 하는 곳입니다. 이 때문에 tanh⁡\tanh 의 미분값도 downstream gradient 를 계산할 때 반영됩니다.
그런데, tanh⁡\tanh 의 그래프를 보시면, 좌우 범위 모두에서 saturation 을 관찰하실 수 있습니다. 이는 tanh⁡\tanh 의 미분값이 양끝 범위에서 0 에 가깝게 수렴한다는 것을 의미하고 downstream gradient 를 계산할 때 chain rule 을 통해서 local gradient 와의 곱 연산이 일어나기 때문에 산출 값이 작아질 수 있겠다- 라는 생각이 드실 겁니다. 추가로, tanh⁡\tanh 의 미분 그래프의 최댓값은 1 이기 때문에 더더욱 activation function 을 지나올 수록 gradient 값이 작아지는 현상이 빈번하게 발생하는 것입니다.
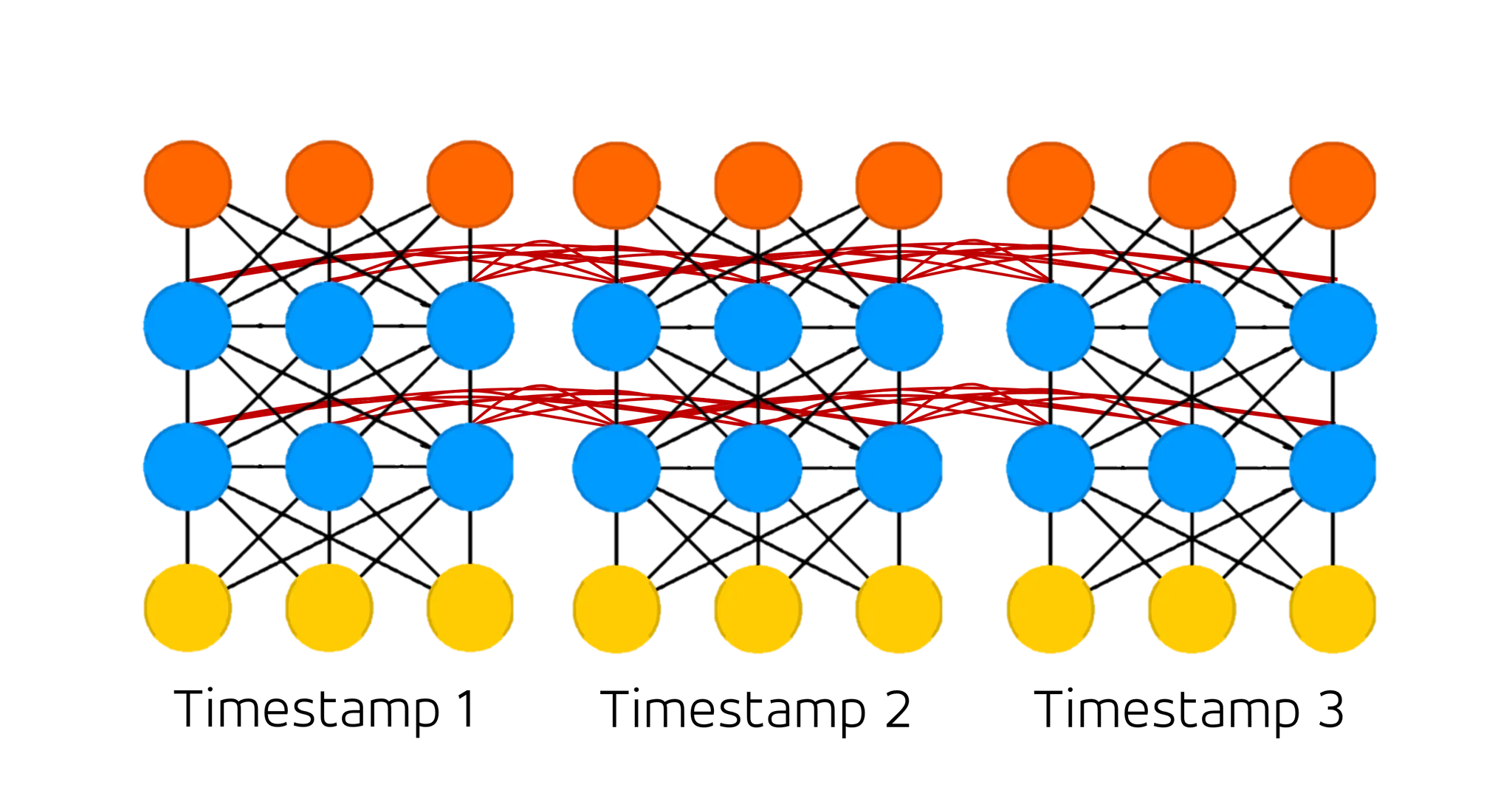
RNN 에서는 network 가 recurrent 하기 때문에 이러한 현상이 심화됩니다. 각 layer 를 지날 때마다 activation function 연산을 실행하게 되는데 forward propagation 시에 input 의 sequential length 에 따라서 굉장히 많은 activation function 을 지나야 할 수 있기 때문입니다. 이러한 경우를 흔히 깊이가 깊은 네트워크라고 말하며 통상적으로 깊이가 깊은 네트워크에서 발생하는 gradient vanishing problem 은 필연적으로 해결해야 하는 문제였습니다.
조금 더 쉽게 한 번 가볼까요?!
RNN 을 설명할 때 다음과 같은 예시를 든 적이 있습니다.
예를 들어, "나는 토요일에 늦게" 라는 단어 뭉치가 있다고 할 때 다음 두 단어 중 어느 것이 뒤에 오기에 적절해 보이시나요?
그리고, 이러한 단어 하나하나는 각 timestamp 의 네트워크의 input 으로 들어가게 된다고 이야기 드린적이 있습니다. 사실 위와 같은 예시에서는 Gradient Vanishing Problem 이 발생하지 않습니다. Input 의 sequential lenth 가 굉장히 짧기 때문입니다. 하지만, 다음과 같은 예시는 어떨까요?
예를 들어, "나는 미국에서 12년간 살다가 한국으로 돌아왔기 때문에" 라는 단어 뭉치가 있다고 할 때 다음 두 단어 중 어느 것이 뒤에 오기에 적절해 보이시나요?
영어고수야
영어초보야
마찬가지로, 한국어가 모국어인 분들이라면 대부분 1번이 더 적절해 보인다고 생각하실 것 같습니다. 다만 여기서 짚고 넘어가야 할 점은 미국이라는 단어와 12년이라는 단어가 "영어고수야" 와 "영어초보야" 가 올 수 있는 위치와 상당히 멀다는 점입니다. 자연스러운 문장의 결과를 산출하기 위해서는 해당 두 단어가 다음에 올 단어에 미치는 영향이 상당히 큼에도 불구하고 말입니다.
이렇게 두 단어 사이의 영향도가 커야 하는 것에 비해서, 단어 사이의 간격이 넓어 gradient 가 소실되어 그 관계적 요소를 반영할 수 없는 문제를 RNN 에서의 Long Term Dependency Problem 이라고 합니다.
Long Short Term Memory(LSTM) 가 해당 문제를 해결한 방법은 각 Cell 에 Memory 를 두는 것입니다. 이를 이해하기 위해서 먼저 Long Short Term Memory(LSTM) 의 연산 설계 방식에 대해서 설명드리려고 합니다. 아래의 글은 제가 Seq2Seq 논문리뷰를 하면서 작성한 글을 발췌한 것입니다.
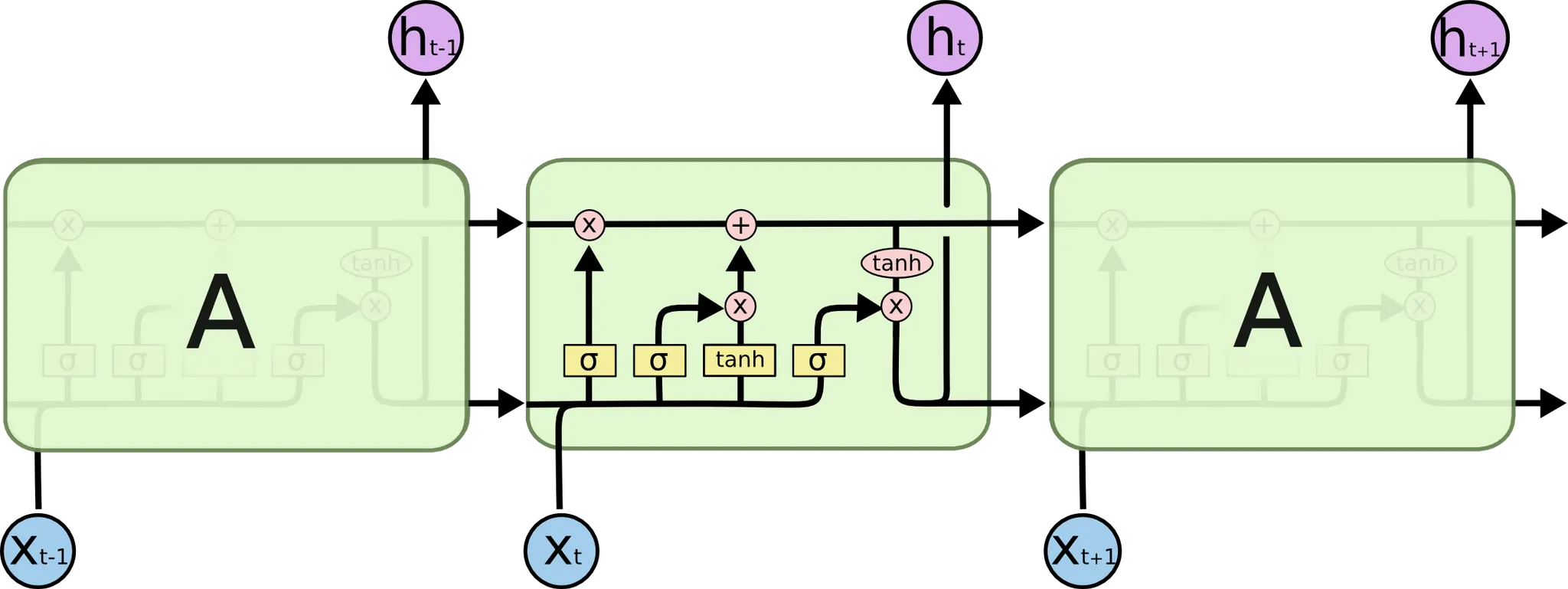
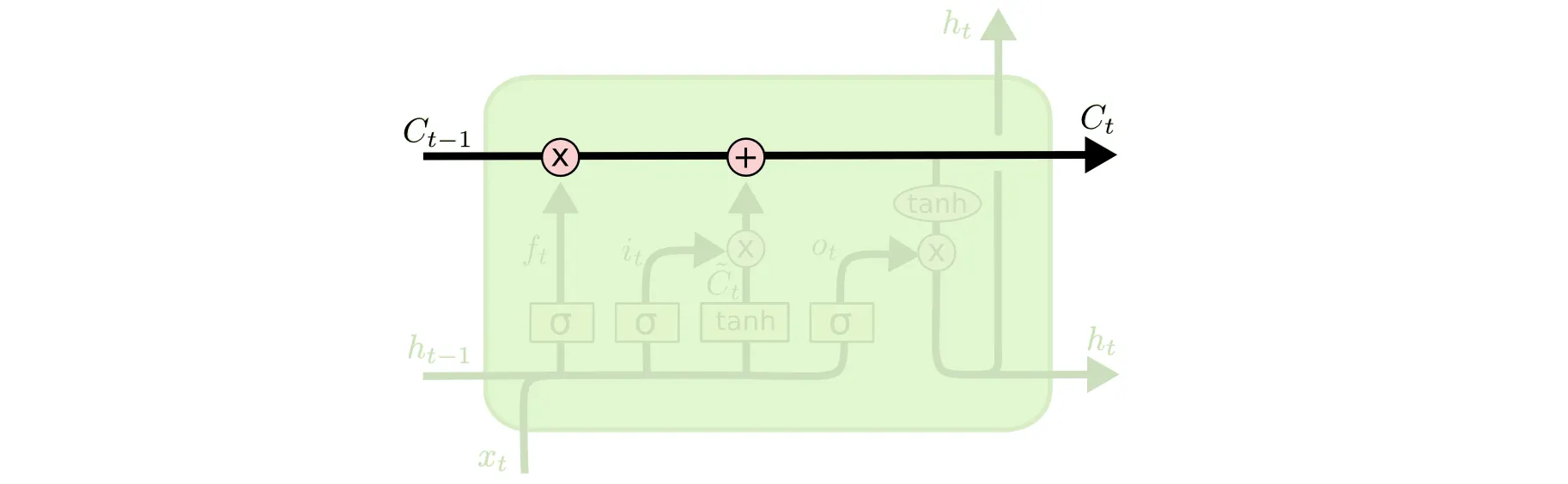
가장 먼저 소개드릴 부분이 Memory 라고 말씀드렸던 Cell State 입니다.
LSTM 의 가장 위쪽 라인을 Cell State 라고 부릅니다. 이 Cell State 라인에서 보이는 + 연산입니다. 저 연산 덕에 Gradient 가 극적으로 작아지는 현상을 해결할 수 있는데 이는 뒤에서 조금 더 설명드리려고 합니다.
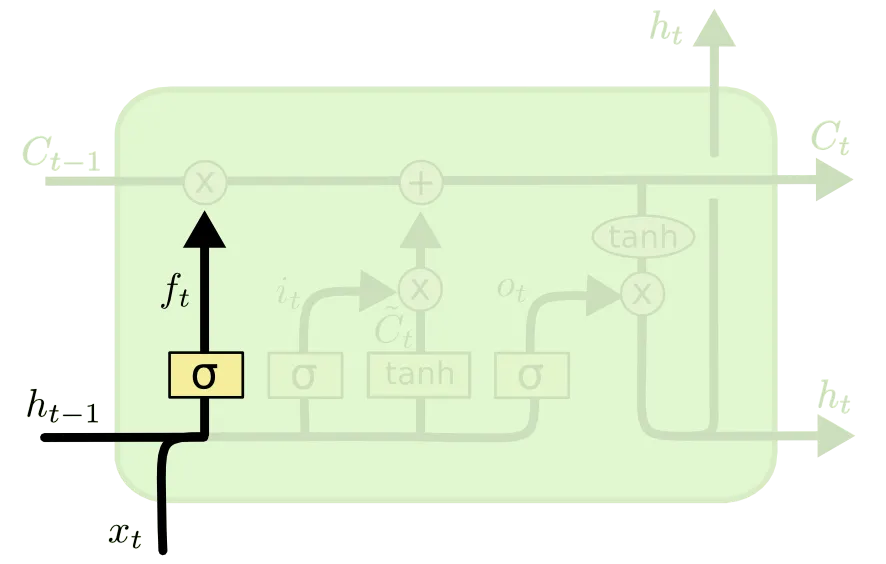
다음으로 소개드릴 부분이 Forget Gate 라고 불리는 부분입니다.
Forget Gate 는 "Past Cell State 를 얼마나 Current Cell State 에 반영할 것인가" 에 대한 항목입니다. 위 그림의 ftf_t가 이 척도를 나타내는 항목이고 이는 아래와 같이 정의됩니다.
ft=σ(Wxfxt+Whfht−1+bf)f_t=\sigma(W_{x_f}x_t+W_{h_f}h_{t-1}+b_f)
앞선 설명과 동일하게 WW항목은 weight 들이며, ftf_t가 0에 가까울 수록 이전의 Cell State 인 Ct−1C_{t-1}은 현재 Cell State 인 CtC_t에 미치는 영향이 작습니다. 말 그대로 이전의 상태를 "잊어버리는 것"이죠. 반대로 ftf_t가 1에 가까울 수록 이전의 상태를 완전히 반영하게 됩니다.
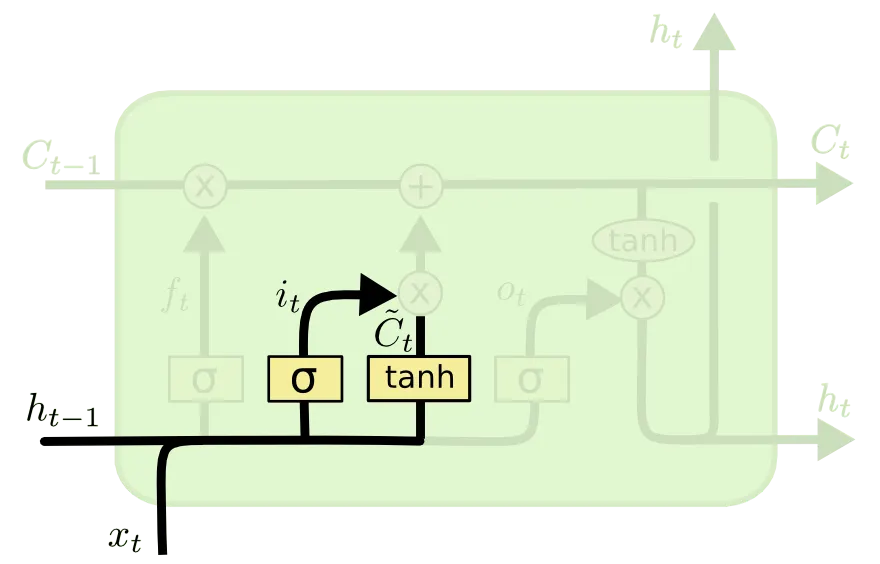
다음으로 소개드릴 부분은 Input Gate 라고 불리는 부분입니다.
Input Gate 는 "input 으로 들어온 정보를 얼마나 기억할 것인가" 에 대한 항목입니다. 위 그림의 iti_t가 이 척도를 나타내는 항목이고 Ct~\tilde{C_t}가 RNN 에서의 Cell State 로 계산된 값과 같은 역할을 하는 친구입니다. 부연 설명을 하자면, 이전 cell 에서 넘어온 hidden state 와 input 만으로 계산해낸 state 라고 볼 수 있습니다. 이들은 아래와 같은 식으로 나타낼 수 있습니다.
it=σ(Wxixt+Whiht−1+bi)Ct~=tanh⁡(WxCxt+WhCht−1+bC)i_t=\sigma(W_{x_i}x_t+W_{h_i}h_{t-1}+b_i)\\ \tilde{C_t}=\tanh(W_{x_C}x_t+W_{h_C}h_{t-1}+b_C)
앞선 설명과 동일하게 WW항목은 weight 들이며, iti_t가 1에 가까울 수록 이전 cell 에서 넘어온 hidden state 와 input 만으로 계산해낸 state 가 현재 Cell State 인 CtC_t에 미치는 영향이 큽니다. 말 그대로 "input 으로 들어온 친구를 기억하는 것이죠". 반대로 iti_t가 0에 가까울 수록 input 의 반영도는 작아집니다.
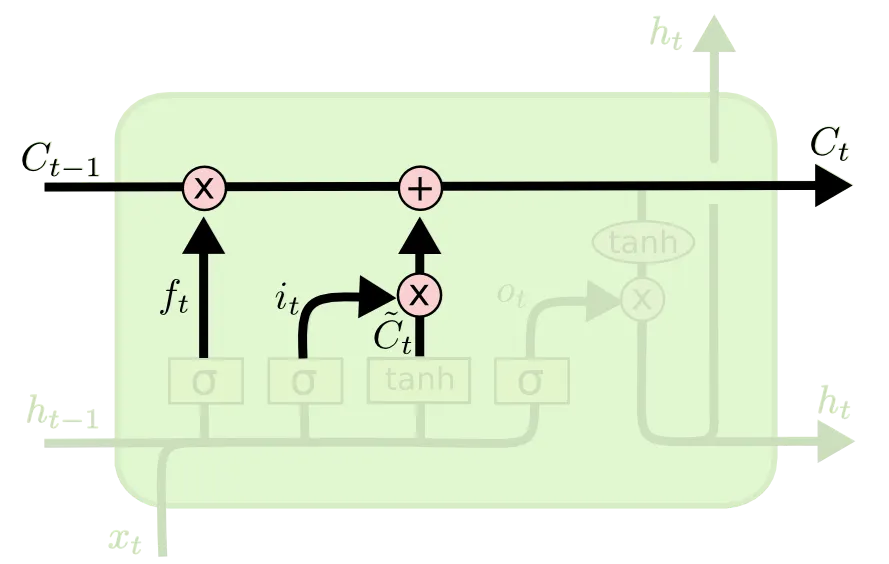
다음으로 소개드릴 부분이 State Update 부분입니다.
이 부분은 제일 처음에 소개드렸던 Cell State 라인에 실제로 Cell State 의 update 가 이루어지는 연산에 대한 부분입니다. Forget Gate 와 Input Gate 의 결과를 합 연산하여 update 한 것이며, 아래와 같은 식으로 다시 나타낼 수 있습니다. 아래 식의 ∗*은 elementwise multiplication 입니다.
Ct=ft∗Ct−1+it∗Ct~C_t=f_t*C_{t-1}+i_t*\tilde{C_t}
Cell State 에 대한 update 를 하면 끝!! 이라고 생각하실 수 있는데 아직 한 부분이 남았습니다. 마지막으로 소개드릴 부분은 Output Gate 라고 불리는 부분입니다.
이 부분은 다음 cell 로 전해질 hidden state 를 산출하는 역할을 합니다. 이전과 마찬가지로 이번에도 Cell State 를 얼마나 반영하여 hidden state 로 산출할지에 대한 척도가 존재합니다. 위 그림의 oto_t가 그 척도입니다. 위 그림의 연산을 식으로 나타내면 다음과 같습니다. 마찬가지로 ∗*은 elementwise multiplication 입니다.
ot=σ(Whoht−1+Whxxt+bo)ht=ot∗tanh⁡(Ct)o_t=\sigma(W_{h_o}h_{t-1}+W_{h_x}x_t+b_o)\\ h_t=o_t*\tanh(C_t)
앞선 설명과 동일하게 WW항목은 weight 들이며, oto_t가 1에 가까울 수록 이전 Cell State 를 온전하게 다음 cell 로 이전할 hidden state 로 변환할 수 있는 것입니다.
여기까지 오시면 Long Short Term Memory(LSTM) 의 구조에 대해서는 다 이해하신 것입니다. 다만, 중요한 이야기 하나를 빠트렸습니다. 왜 위와 같은 설계가 Long Term Dependency 문제를 해결한 것인지에 대해서 말입니다.
결론부터 말씀드리자면, Cell State 라고 부른 가장 위쪽 라인이 activation function 을 거치지 않고도 다음 recurrent network 로 연결할 수 있는 free path 역할을 할 수 있기 때문입니다. 해당 path 를 통한 backward propagation 의 경우에 기존보다 더 큰 scale 의 gradient 를 네트워크의 앞쪽에 전달할 수 있었기 때문이라고 보시면 됩니다.
이렇게 이번 세션에서는 Recurrent Neural Network 의 Long Dependency Problem 을 해결한 네트워크인 Long Short Term Memory (LSTM) 에 대해서 알아보는 시간을 가졌습니다. 이번 세션을 통해서 일반적인 Gradient Vanishing Problem 와 Recurrent Neural Network 에서의 Long Dependency Problem 이 무엇인지, 그리고 이를 Long Short Term Memory (LSTM) 에서 어떻게 해결했는지에 대해서 알아두시면 좋을 것 같습니다.