Seq2Seq

분야
Machine Translation
리뷰 날짜
2021/04/20
본 포스트에서는 Sequential 데이터를 사용해 End-To-End Machine Translation 을 진행한 논문에 대해서 리뷰하려고 합니다. 리뷰하려는 논문의 제목은 다음과 같습니다.
“Sequence to Sequence Learning with Neural Networks”
논문에 대한 내용을 직접 보시고 싶으신 분은 이곳을 참고하시면 좋습니다.

Objective

논문의 배경은 다양한 분야의 연구들에서 다루는 문제들이 길이를 특정할 수 없는 sequence 데이터를 다루는 것에서 시작합니다. Speech Recognition(음성 인식), Machine Translation(기계 번역) 이 그 예시들이며, 이러한 분야들은 input 과 target 이 고정된 dimenstion 을 가지는 일반적인 DNN(Deep Neural Network) 으로는 다룰 수 없다는 문제점이 있었습니다.
이러한 문제를 해결하기 위해서 논문에서는 input sequence 를 읽어들이는 과정과 연산을 거친 후 산출된 vector 로부터 output 을 산출하는 과정 모두에 LSTM(Long Short-Term Memory) 을 사용합니다. 이렇게 설계한 결과 모델이 문장의 의미를 표현하는 방법을 학습하여 비슷한 의미의 문장은 비슷하게, 다른 의미의 문장은 다르게 번역할 수 있었다고 합니다. 이는 wording 자체의 의미에 집착하지 않고 문맥의 의미에 맞는 번역을 할 수 있었기 때문이고, 대표적으로 수동태나 능동태 문장의 번역 결과가 다르지 않았음을 보여주었습니다.
LSTM 이 그러면 뭔데 ???? 라고 물으실 분들이 있으실 것 같습니다. 이에 대한 내용은 Background 에서 이어서 설명을 드리겠습니다.

Background

LSTM 에 대한 이해를 하기 위해선, RNN 에 대한 이해가 필요합니다. Background 에서는 이 두 네트워크에 대해서 소개를 드리려고 합니다.

RNN (Recurrent Neural Network)

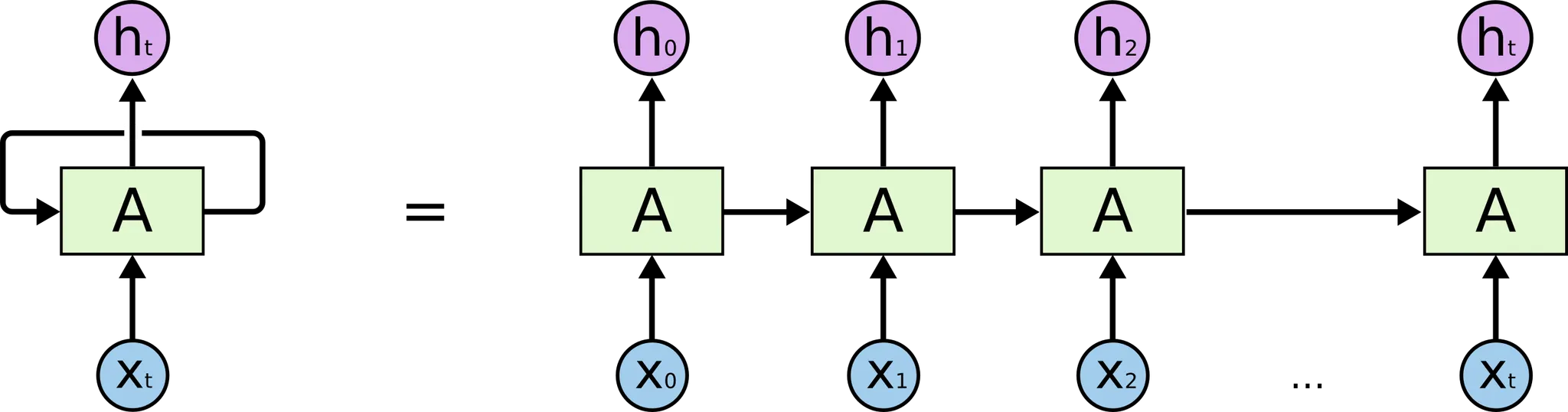
RNN 은 sequential data 의 학습을 위해 설계된 네트워크 구조입니다. 이름에 들어가 있는 recurrent 는 RNN 의 한 cell 의 output 이 다른 cell 의 input 으로 들어가 반복적인 구조를 가지고 있음을 의미합니다.
위 그림과 같이 보통 RNN 은 좌측의 구조로 표현하는데, 좌측 그림으로 표현하면 실질적으로 우측 구조를 가지고 있음을 뜻합니다. 눈치가 빠르신 분들은 sequential data 가 순서가 존재하기 때문에 이렇게 과거 데이터를 넘겨받는 반복적인 형태로 구성되어 있다는 것을 알아채셨을 것이라 생각합니다.
RNN 의 모든 cell 에서는 동일한 작업이 반복됩니다. 각 cell 마다 xtx_t가 input 으로 들어오고, hth_t가 output 으로 나옵니다. 그리고, 위 그림에는 명시되어 있지 않지만, 다음 cell 으로 전달되는 vector 성분이자 hidden state 인 gtg_t도 존재합니다.
이 때, gtg_t를 산출하기 위한 activation function 을 f1f_1이라 하고, hth_t를 산출하기 위한 activation function 을 f2f_2라 한다면, RNN 의 한 cell 에서 발생하는 연산은 다음과 같이 나타낼 수 있습니다.
gt=f1(Wgtgt−1+Wxtxt+bt)ht=f2(Whtgt)g_t=f_1(W_{g_t}g_{t-1}+W_{x_t}x_t+b_t)\\ h_t=f_2(W_{h_t}g_t)
위에서 적은 WgtW_{g_t},WxtW_{x_t},WhtW_{h_t} 는 모두 weight 입니다. 한 cell 당 서로 다른 3개의 weight vector 를 정의해야 하는 것이죠. 결국, 이 세 가지 weight 들을 학습시켜 sequential data 의 특성을 추출해내는 것으로 보시면 됩니다.
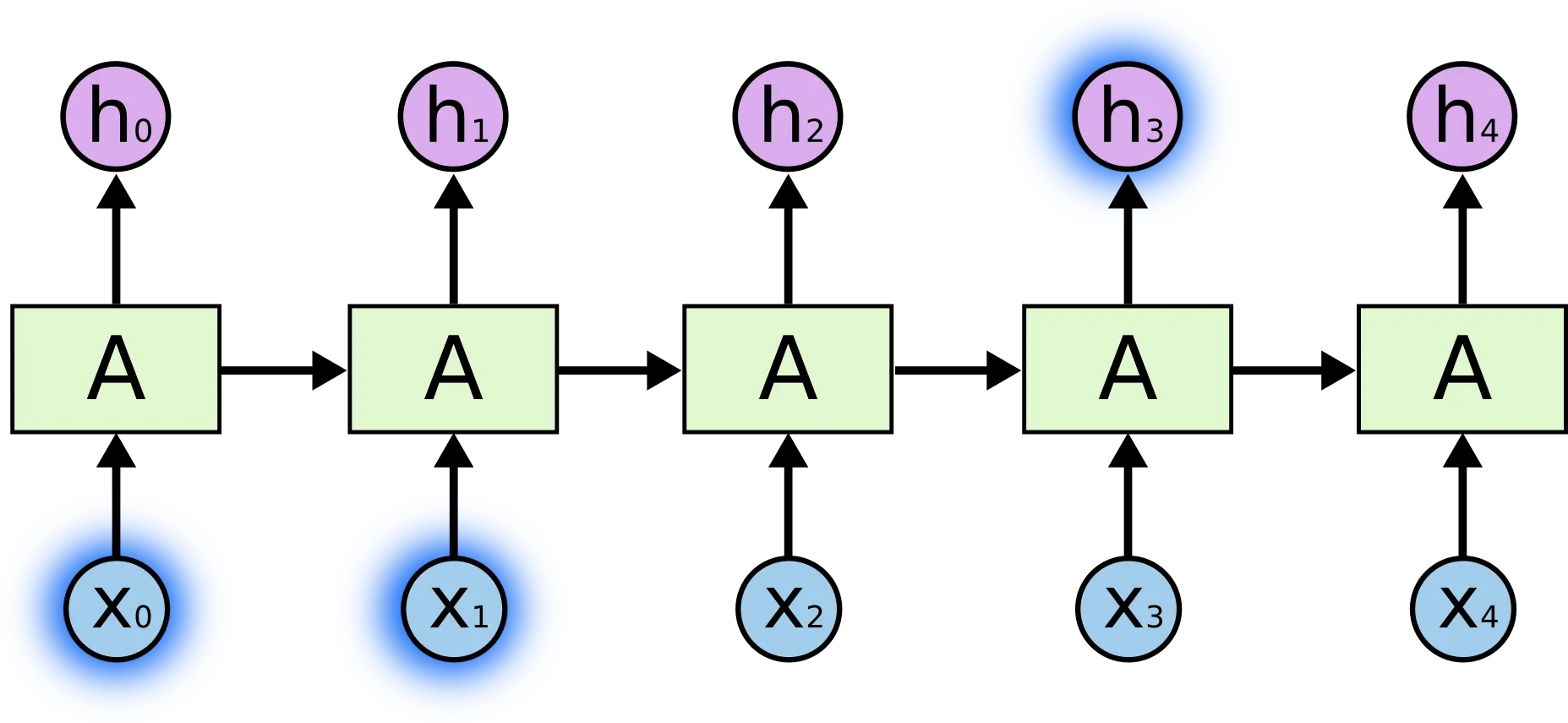
그런데, RNN 에는 치명적인 단점이 존재합니다. ResNet 에서도 해결하려고 했던 Gradient Vanishing 이 발생한다는 점입니다. 이는 activation function 으로 사용하는 tanh, sigmoid 의 미분 항의 값이 수렴 지점 근처에서 매우 작은 값을 가지는 데다가, 이러한 값이 cell 을 통해 전달되면서 곱적용이 일어나면서 한 cell 의 weight 가 실제로 다른 cell 의 산출 값에 매우 적은 영향을 주는 현상입니다. 아래의 그림을 예시로 들자면,
위 그림의 x0x_0와 x1x_1이 h3h_3의 결과에 주는 영향은 cell 거리가 멀지 않기 때문에 그리 작지 않습니다.
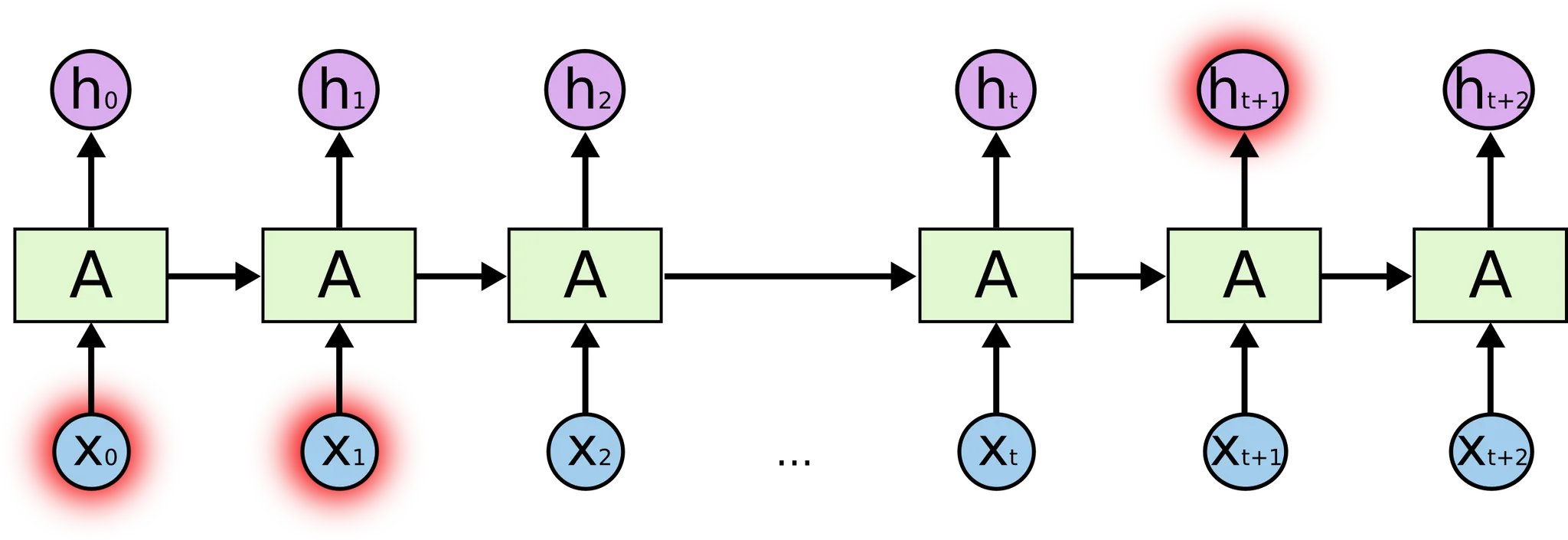
하지만, 위 그림의 x0x_0와 x1x_1이 ht+1h_{t+1}에 주는 영향은 cell 간 거리가 멀기 때문에 굉장히 작습니다. 이렇게 설계될 경우, sequential data 에서 거리가 먼 곳의 두 데이터 값이 실제로 유의미한 특성을 가지고 있을 경우 모델 성능의 큰 저하로 이어질 수 있습니다. 이를 Long Term Dependency Problem 이라고 합니다.
이러한 현상을 해결하기 위해 등장한 모델이 LSTM 입니다.

LSTM (Long Short-Term Memory)

LSTM 은 앞서 설명한 Gradient Vanishing 현상을 해결할 수 있는 네트워크 구조입니다. ResNet 이 사용한 방법과 유사한데, cell 내에 이전 hidden state 를 일부 유지할 수 있는 합 연산을 두어, cell 을 거쳐도 어느 정도 gradient 를 유지할 수 있습니다.
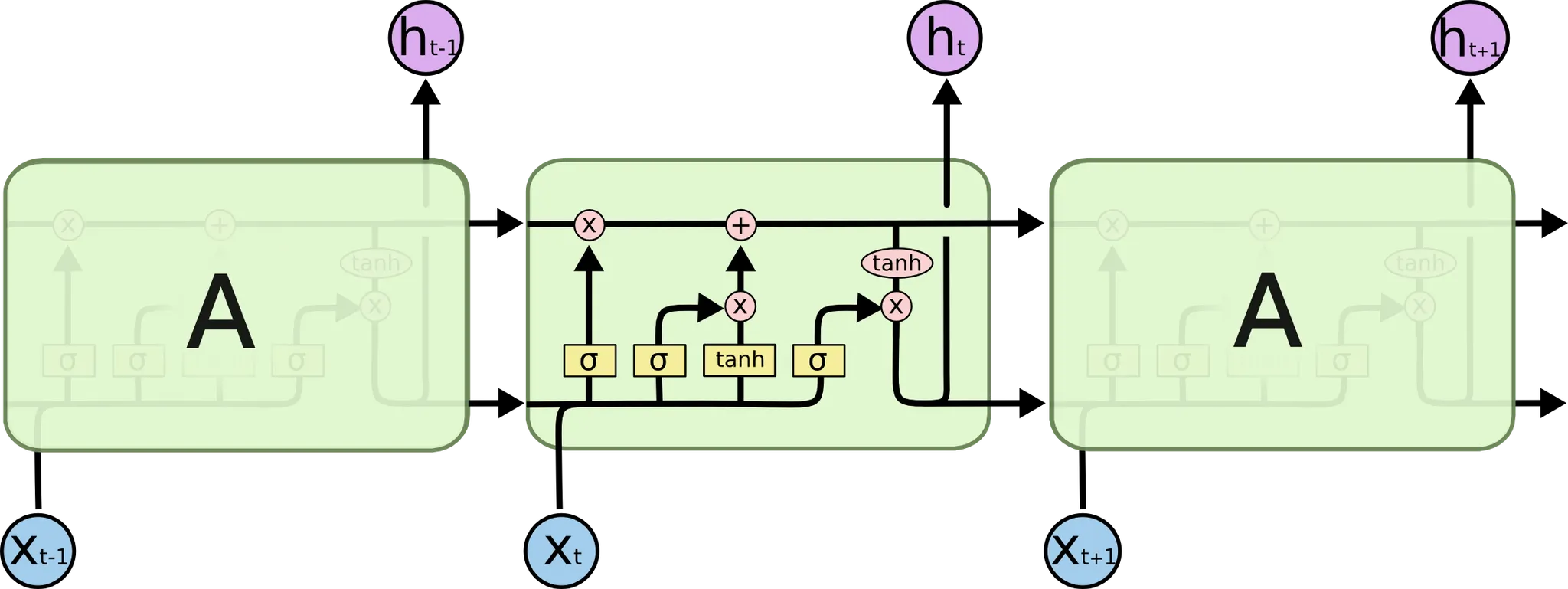
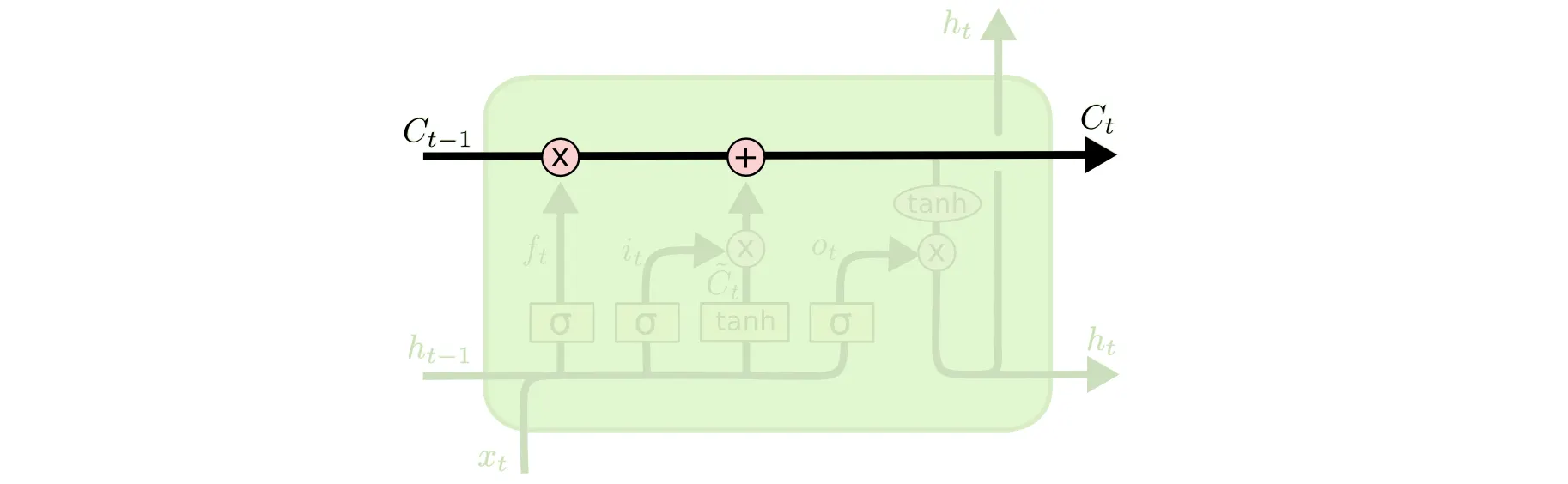
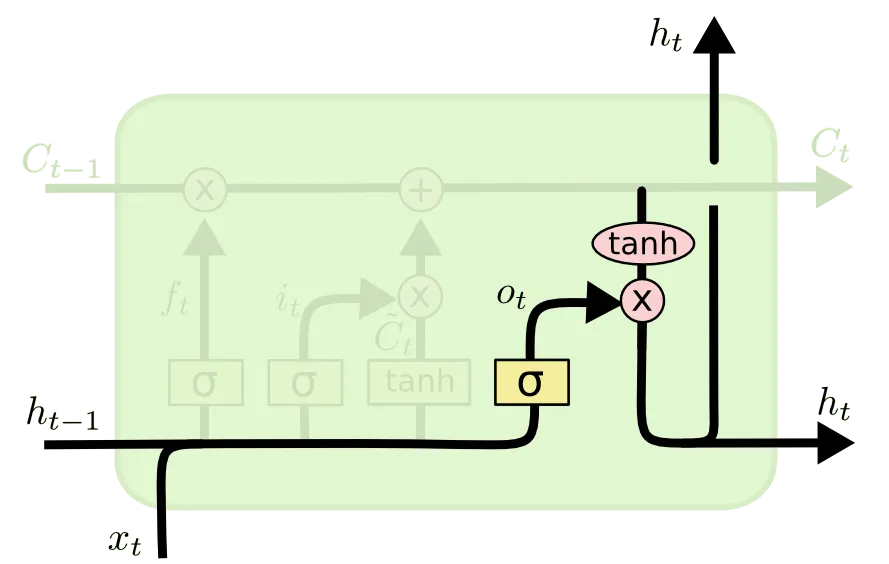
LSTM 의 세부적인 구조는 위 그림의 가운데 cell 의 내부와 같습니다. 이를 설명하기 위해 각각을 세부 부분으로 나누어 설명을 드리려고 합니다.
가장 먼저 소개드릴 부분이 Cell State 입니다.
LSTM 의 가장 위쪽 라인을 Cell State 라고 부릅니다. 앞서 이전의 Cell State 를 일부 유지할 수 있는 합 연산을 둔다고 말씀드렸습니다. 그것이 이 Cell State 라인에서 보이는 + 연산입니다. 저 연산 덕에 Gradient 가 극적으로 작아지는 현상을 해결할 수 있었던 것입니다.
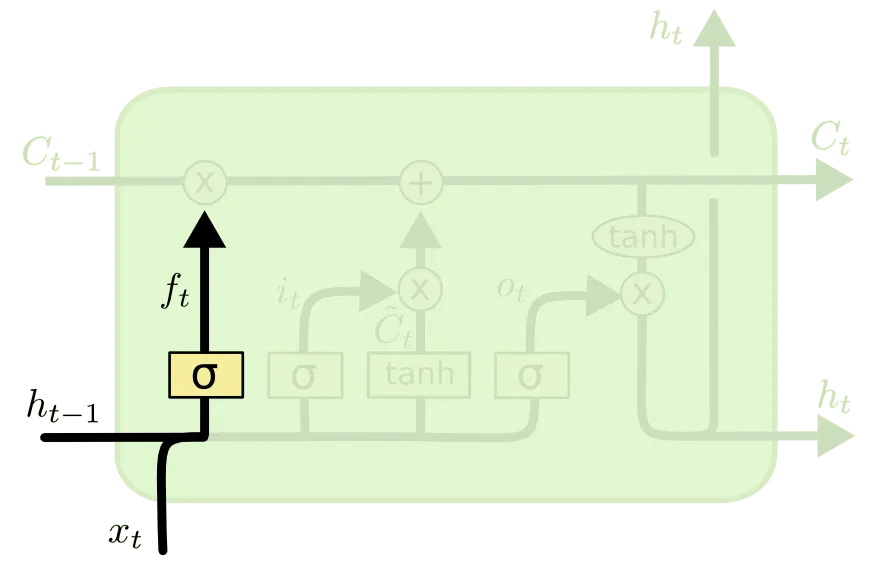
다음으로 소개드릴 부분이 Forget Gate 라고 불리는 부분입니다.
Forget Gate 는 "Past Cell State 를 얼마나 Current Cell State 에 반영할 것인가" 에 대한 항목입니다. 위 그림의 ftf_t가 이 척도를 나타내는 항목이고 이는 아래와 같이 정의됩니다.
ft=σ(Wxfxt+Whfht−1+bf)f_t=\sigma(W_{x_f}x_t+W_{h_f}h_{t-1}+b_f)
앞선 설명과 동일하게 WW항목은 weight 들이며, ftf_t가 0에 가까울 수록 이전의 Cell State 인 Ct−1C_{t-1}은 현재 Cell State 인 CtC_t에 미치는 영향이 작습니다. 말 그대로 이전의 상태를 "잊어버리는 것"이죠. 반대로 ftf_t가 1에 가까울 수록 이전의 상태를 완전히 반영하게 됩니다.
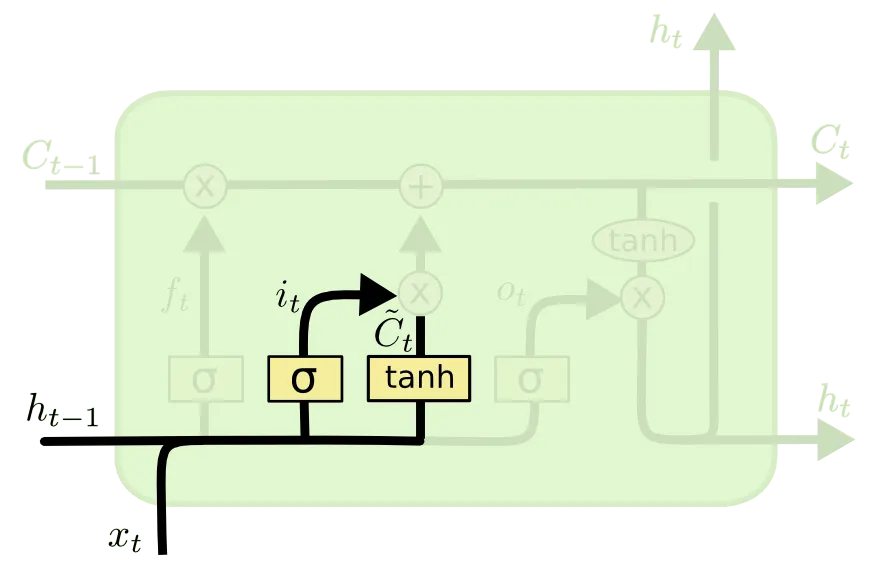
다음으로 소개드릴 부분은 Input Gate 라고 불리는 부분입니다.
Input Gate 는 "input 으로 들어온 정보를 얼마나 기억할 것인가" 에 대한 항목입니다. 위 그림의 iti_t가 이척도를 나타내는 항목이고 Ct~\tilde{C_t}가 RNN 에서의 Cell State 로 계산된 값과 같은 역할을 하는 친구입니다. 부연 설명을 하자면, 이전 cell 에서 넘어온 hidden state 와 input 만으로 계산해낸 state 라고 볼 수 있습니다. 이들은 아래와 같은 식으로 나타낼 수 있습니다.
it=σ(Wxixt+Whiht−1+bi)Ct~=tanh⁡(WxCxt+WhCht−1+bC)i_t=\sigma(W_{x_i}x_t+W_{h_i}h_{t-1}+b_i)\\ \tilde{C_t}=\tanh(W_{x_C}x_t+W_{h_C}h_{t-1}+b_C)
앞선 설명과 동일하게 WW항목은 weight 들이며, iti_t가 1에 가까울 수록 이전 cell 에서 넘어온 hidden state 와 input 만으로 계산해낸 state 가 현재 Cell State 인 CtC_t에 미치는 영향이 큽니다. 말 그대로 "input 으로 들어온 친구를 기억하는 것이죠". 반대로 iti_t가 0에 가까울 수록 input 의 반영도는 작아집니다.
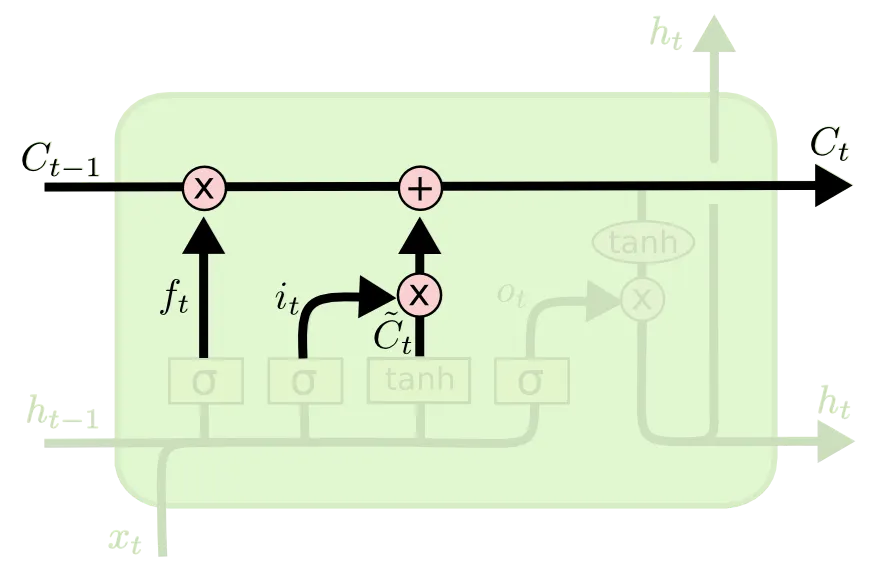
다음으로 소개드릴 부분이 State Update 부분입니다.
이 부분은 제일 처음에 소개드렸던 Cell State 라인에 실제로 Cell State 의 update 가 이루어지는 연산에 대한 부분입니다. Forget Gate 와 Input Gate 의 결과를 합 연산하여 update 한 것이며, 아래와 같은 식으로 다시 나타낼 수 있습니다. 아래 식의 ∗*은 elementwise multiplication 입니다.
Ct=ft∗Ct−1+it∗Ct~C_t=f_t*C_{t-1}+i_t*\tilde{C_t}
Cell State 에 대한 update 를 하면 끝!! 이라고 생각하실 수 있는데 아직 한 부분이 남았습니다. 마지막으로 소개드릴 부분은 Output Gate 라고 불리는 부분입니다.
이 부분은 다음 cell 로 전해질 hidden state 를 산출하는 역할을 합니다. 이전과 마찬가지로 이번에도 Cell State 를 얼마나 반영하여 hidden state 로 산출할지에 대한 척도가 존재합니다. 위 그림의 oto_t가 그 척도입니다. 위 그림의 연산을 식으로 나타내면 다음과 같습니다. 마찬가지로 ∗*은 elementwise multiplication 입니다.
ot=σ(Whoht−1+Whxxt+bo)ht=ot∗tanh⁡(Ct)o_t=\sigma(W_{h_o}h_{t-1}+W_{h_x}x_t+b_o)\\ h_t=o_t*\tanh(C_t)
앞선 설명과 동일하게 WW항목은 weight 들이며, oto_t가 1에 가까울 수록 이전 Cell State 를 온전하게 다음 cell 로 이전할 hidden state 로 변환할 수 있는 것입니다.
설명이 길었는데 정리하자면,
LSTM 은 Cell State 와 hidden state 라는 개념으로 cell 의 상태를 나누어, 각각의 셀마다 이전의 Cell State 와 현재의 input 으로 계산한 Cell State 가 얼마나 현재의 Cell State 에 영향을 줄지에 대한 척도는 물론, 최종적인 output hidden state 를 얼마나 Cell State 를 반영하여 산출할지에 대한 척도를 학습하는 방법을 사용했습니다. 특히 Forget Gate 와 Input Gate 의 합 연산 구조로 Gradient Vanishing 문제를 완화했다는 것에 의미가 있습니다.
LSTM 이라는 이름의 "Short-Term" 은 각 cell 이 저장하는 weight가 sequential data 각각을 해석할 수 있음을 의미하며, "Long-Term" 은 각각의 cell 이 전달하는 hidden state 를 Gradient Vanishing 을 완화하여 긴 sequence 에 까지 전달할 수 있음을 의미합니다.
휴... 길었는데 지금까지 Background 에 대한 설명을 마쳤고, 이제 논문에서 설계한 모델에 대해서 알아봅시다 !!

Model

앞서 Background 를 장황하게 설명드린 것에 비해 Seq2Seq 만의 모델은 복잡하지 않습니다.
전통적인 RNN 의 경우, sequence input x1,x2,...,xTx_1, x_2,...,x_T에 따른 sequence output y1,y2,...,yTy_1,y_2,...,y_T에 대해서 다음과 같은 연산으로 weight 를 학습합니다.
ht=sigm(Whxxt+Whhht−1)yt=Wyhhth_t=sigm(W_{h_x}x_t+W_{h_h}h_{t-1})\\ y_t=W_{y_h}h_t
이전에 설명했던 형태에서 activation function 가 구체화 되고, bias 가 사라졌을 뿐 동일한 형태죠?
하지만 전통적인 RNN 의 경우에 input, output length 가 다르고 그 관계가 non-monotonic 한 sequential data 를 다룰 수 없습니다.
이에 대한 개선으로 Cho et al. 과 같은 논문에서는 input sequence 를 하나의 RNN 을 통해서 fixed-size vector 로 변홚시킨 후, vector 를 다시 RNN 으로 sequence 로 만드는 방법을 제안했습니다. 하지만 이 방법은 앞서 RNN 에서 설명했던 대로 Long Term Dependency 를 학습하기엔 어려웠고 이를 LSTM 으로 바꾼 구조를 제시합니다.
논문에서는 LSTM 의 목적을 input sequence x1,x2,...,xTx_1, x_2,...,x_T에 따른 sequence output y1,y2,...,yT′y_1,y_2,...,y_{T'}의 확률 분포를 학습하는 것으로 정의합니다. 이는 주어진 input sequence 에 해당하는 가장 적합한 output sequence 를 찾기 위함으로 볼 수 있습니다.
그리고 이 확률을 다음과 같은 수식으로 구해냅니다.
Pr⁡(y1,y2,...,yT′∣x1,x2,...,xT)=∏t=1T′Pr⁡(yt∣v,y1,..,yt−1)\Pr(y_1,y_2,...,y_{T'}|x_1,x_2,...,x_T)=\prod_{t=1}^{T'}\Pr(y_t|v,y_1,..,y_{t-1})
위 식의 우항의 vv는 x1,x2,...,xTx_1, x_2,...,x_T 의 fixed dimensional representation 으로 보시면 됩니다. Latent Factor 라고 생각하시면 편합니다. 그리고 우항의 product 내부의 probability 는 전체 vocabulary 에 대한 softmax layer 의 결과를 나타냅니다. Input 의 Latent Factor 가 vv 이고 결과의 초기 부분이 y1,y2,...,yt−1y_1,y_2,...,y_{t-1}로 나타났을 때 다음 결과가 yt−1y_{t-1}로 나타날 확률인 것이죠. 눈치채셨겠지만 이는 결국 t 번째 cell 의 output 입니다.
결국, tt가 1부터 T′T'까지 해당 probability 를 모두 곱하면 주어진 input sequence 에 대한 특정 output sequence 가 등장할 확률을 구해낼 수 있는 것입니다.
위 내용이 이해되지 않는 분을 위해... 간단히 부연 설명하겠습니다. A 일때 B 일 확률이 0.5 이고, B 일때 C 일 확률이 0.1 이면 A 일때 B 이고 C 일 확률이 0.05 인 것을 알 수 있죠? 위와 같습니다. Input 이 v 일 때 첫 번째 output 이 y1y_1일 확률이 aa 라고 합시다. 첫 번째 output 이 y1y_1일때 두 번째 output 이 y2y_2 일 확률이 bb 라고 합시다. 두 번째 output 이 y2y_2일 때 세 번째 output 이 y3y_3 일 확률이 cc 라고 합시다. 그러면, Input 이 v 일 때 첫 번째 output 이 y1y_1이고 두번 째 output 이 y2y_2이고 세 번째 output 이 y3y_3 일 확률은 abcabc 입니다. 그런데, 이는 Input 이 v 일 때 첫 번째가 y1y_1, 두 번째가 y2y_2, 세 번째가 y3y_3 인 확률과 같죠. 결국 input 에 따른 특정 output 의 확률을 구해낸다는 것입니다.
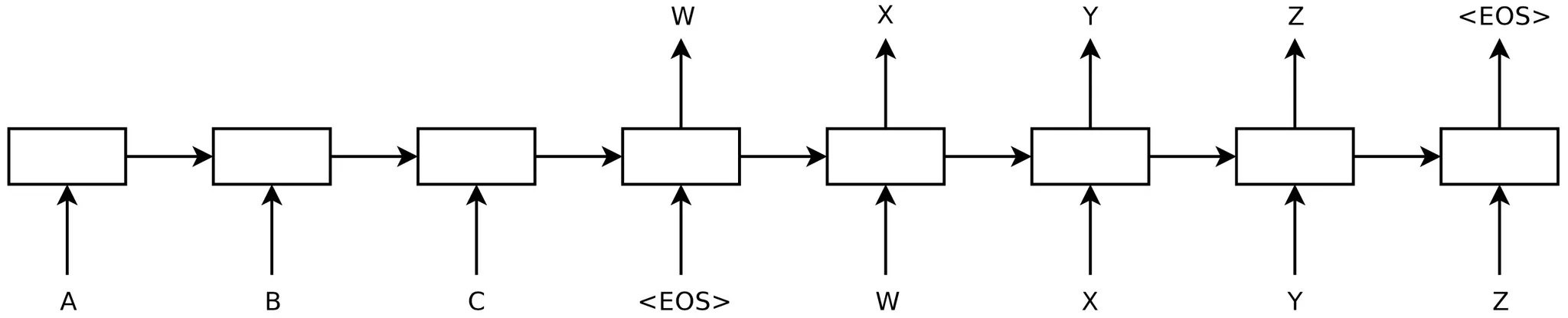
더불어, 논문에서는 모델의 input, output 의 길이에 대한 제약을 두지 않기 위해 <EOS> symbol 을 두어 문장의 끝을 알리는 특수 문자를 만들었습니다. (알아보신 분들도 계시겠지만 End of Sentence 의 약어입니다.)
위 그림이 논문에서 <EOS> symbol 을 사용한 방법입니다. <EOS> symbol 이 나타나면 그 뒤로부터 나타나는 output 을 가지고 train 에서는 loss 를 구하고, test 에서는 output 을 구하는 것입니다. 마찬가지로, <EOS> symbol 이 output 으로 나타나면 종료로 판단합니다. 위 예시에서는 ABC 라는 문장을 넣어 WXYZ 라는 문장을 얻은 것입니다.
논문에서는 위에서 설명한 모델과 방법을 베이스로 한 학습을 진행했습니다. 하지만, 논문에서는 위에서 언급한 것 이외에도 특별하게 언급할 그들 모델의 특징들을 세 가지 정도 언급하고 넘어갑니다. 다음이 그 세가지 특징들입니다.
1.
논문에서는 두 개의 다른 LSTM 집합을 사용했습니다. 하나는 input sequence 를 위한 것이고, 다른 하나는 output sequence 를 위한 것입니다. 이렇게 두 개의 LSTM 집합을 사용한 것은 model parameter 수를 늘려서 무시할 수 없는 수준의 computational cost 를 증가시켰지만 논문에서는 다중 언어 쌍으로 동시에 학습을 할 수 있는 용이한 설계를 진행하기 위해 이와 같이 설계를 진행합니다.
2.
Deep LSTM 을 사용했습니다. 당연한 소리일 수도 있지만 Deep LSTM 이 Shallow LSTM 보다 성능이 좋았고, 최종적으로 Layer 가 4개인 LSTM 을 사용했습니다.
3.
Input Sentence 의 word 순서를 reverse 하여 학습했습니다. 이게 무슨 소리냐 하면... 원래는 ABC 로 input sequence 를 넣었다면 CBA 로 input sequence 를 넣는 것으로 바꾸었다는 것입니다. (A, B, C 각각이 word 입니다.) 이러한 시도는 SGD 가 input-output 간의 관계 설립하기 쉽도록 만들어 주었습니다. 이 내용은 뒤에서도 서술됩니다.
이것으로 논문의 Model 에 대해서 알아보았습니다. 다음으로 논문이 진행한 실험 및 평가에 대해서 알아보도록 하겠습니다..!!

Experiment

논문에서는 WMT'14 English to French MT task 를 기반으로 실험을 진행했습니다. 이 task 도 크게 두 가지로 나누어 진행했는데,
1.
SMT system 사용 없이 directly translate 한 경우
2.
SMT baseline 을 가지고 n-best lists 를 rescore 한 경우
가 그 둘입니다. 이는 뒤에서 결과에 대해서 설명할 때 다시 등장할 것입니다.
여기서 SMT 라 하면, Statistical Machine Translation 의 약어로, 통계적 기계 번역 방법이라고 보시면 됩니다.

Dataset Detail

논문에서는 그들이 사용한 데이터셋에 대한 정보를 제공합니다. 제가 보았을 때 특별하게 주목해야 할 내용은 없었지만, 간단하게 공유드리면 다음과 같습니다.
논문에서 사용한 데이터셋은 348M 의 French words 와 304M 의 English words 를 기반으로 한 12M sentences 의 subset 으로 이루어져 있다고 합니다. 또한 source sentence 에 사용할 160,000 개의 vocabulary 를, target sentence 에 사용할 80,000 개의 vocabulary 를 선정했습니다. 이렇게 선정한 vocabulary 에 속하지 않는 word 들은 특별한 "UNK" token 으로 치환했다고 합니다.

Decoding and Rescoring

논문에서 설계한 모델을 가지고 학습을 진행할 때 사용할 object 를 이 부분에서 언급합니다.
1∣S∣∑(T,S)∈Slog⁡p(T∣S)\frac{1}{|S|}\sum_{(T,S)\in S}\log p(T|S)
위 식에서 SS는 source sentence 를, TT는 target sentence 를 의미합니다. 즉, 주어진 source sentence 에 대해서 target sentence 가 등장할 확률의 log summation 를 최대화 하는 것을 목적으로 한다고 보시면 됩니다. 그리고 이런 목적은 다음과 같이도 나타낼 수 있습니다.
T^=arg⁡max⁡Tp(T∣S)\hat{T}=\arg\max_Tp(T|S)
앞서 설명한 것처럼 optimal 한 TT 가 주어진 SS 에 대해서 max⁡p(T∣S)\max p(T|S)를 최대화 시키는 T 인 것을 저희는 잘 알고 있습니다.
앞서, p(T∣S)p(T|S) 를 구하기 위해서 이전 sequence 까지의 확률을 가정한 채 다음 sequence data 가 붙을 확률을 구한 뒤 이전 sequence 까지 나타날 확률에 곱하는 것을 반복해 간다고 말씀드렸습니다. 그런데, vocabulary 개수가 몇만이 넘는데 이들을 곱연산으로 가지를 뻗어나가면서 모두 확인해나가면 연산량이 기하급수적으로 늘어납니다. 논문과 선행연구들에서는 이러한 것을 해결하기 위해서 left-to-right beam search decoder 를 사용합니다. 이는 다음 cell 로 연산이 넘어갈 때 vocabulary 수 만큼 경우의 수가 곱해지는데, 이 중에서 가장 높은 BB 개의 후보군만 남기고 나머지는 제거하는 방법론입니다.
이렇게 진행하면 매 cell 마다 B∗NumberOfVocabB*NumberOfVocab 만큼의 후보군만 탐색하면 되기 때문에 연산의 수를 매우 줄일 수 있습니다. 이 BB 를 beam size 라고 칭합니다.
논문에서는 앞서 이야기한대로 baseline system 으로 생성되 1000-best list 를 rescoring 하는 형태의 평가도 진행했는데, 이 때 논문에서 설계한 LSTM 구조로 뽑아낸 1000-best hypothesis 의 log probability 를 가지고 average 를 한 값을 기존의 것과 비교했다고 합니다.

Reversing the Source Sentences

논문에서는 앞서 언급한 논문 모델의 세 가지 특징 중 세 번째 특징인, input sentence 를 reverse 하여 학습을 시킨 것에 대한 실험을 진행했고, 실제로 다음과 같은 결과를 얻었습니다.
1.
LSTM 의 test perplexity 가 5.8 에서 4.7 로 감소했습니다.
2.
LSTM 의 test BLEU scores 가 25.9 에서 30.6 으로 증가했습니다.
여기서 잠깐..!! Perplexity 랑 BLEU scores 가 무엇인지 궁금하실 분들을 위해.... Perplexity 는 길이가 N 인 ground truth target sentence sequence (y1,y2,...,yN)(y_1,y_2,...,y_N) 에 대해서 1P(y1,y2,...,yN)N\sqrt[N]{\frac{1}{P(y_1,y_2,...,y_N)}} 값을 나타냅니다. 즉, 작을수록 정확한 metric 입니다. BLEU score 를 알기 위해서는 먼저 n-gram precision 에 대해서 알아야합니다. n-gram precision 은 전체 n-gram 쌍 중 prediction sentece 와 ground truth sentence 가 일치하는 n-gram 쌍의 개수 비율입니다. 여기서 n-gram 은 연속된 n 개의 단어 집합으로 보시면 됩니다. 다음과 같은 예시를 봅시다. "나는 어두운 방에서 기도를 했다" 라는 ground truth sentence 와, "나는 어둠의 공간에서 기도를 했다." 라는 prediction sentence 가 있다고 하면, 1-gram precision 의 경우 전체 1-gram 쌍은 5개이고, 일치하는 1-gram 쌍은 3개이므로 35\frac{3}{5} 이고, 2-gram precision 의 경우 전체 2-gram 쌍은 4개이고, 일치하는 2-gram 쌍은 1개이므로 14\frac{1}{4} 입니다. 이렇게 n-gram precision을 precisioniprecision_i 라고 칭했을 때, BLEU score 는 min⁡(1,prediction_sentence_lengthground_truth_sentence_length)(∏i=14precisioni)14\min(1, \frac{prediction\_sentence\_length}{ground\_truth\_sentence\_length})(\prod_{i=1}^4 precision_i)^{\frac{1}{4}} 로 정의할 수 있습니다. 즉 클수록 정확한 metric 입니다.
논문에서 위 결과에 대해서 뚜렷한 설명을 해주지는 않습니다만, reversed input sentence 의 경우에 "short term dependency 가 많기 때문에 학습이 잘 되지 않을까" 라는 언급을 합니다. 이것이 무슨 소리인가 하면.... Input sentence 를 reverse 하던 하지 않던 ground truth 와 input sentence 속에서 매칭되는 단어 쌍의 거리의 평균을 생각하면 별 차이가 없겠지만, reverse 하기 전 기준 input sentence 의 앞에 존재하는 단어들은 극적으로 ground truth output sentence 의 매칭되는 단어와의 거리가 가까워진다는 것입니다. 이러한 현상은 backpropagation 이 source sentence 와 target sentence 간의 관계를 설립하기에 용이하게 하고 부분적으로 performance 를 올린 요소라고 보고 있습니다. 더불어, 실험적으로 나타난 결과는 이러한 performance 증가가 단순히 초기 단어의 적중률만의 문제가 아니었다고 합니다.

Training Details & Parallelization

논문에서는 학습에 사용한 parameter 와 간단한 학습 결과 정보를 제공합니다. 다음은 그 정보들입니다.
1.
4 개의 layer 를 사용하고 1개의 layer 에 1000 개의 cell 이 존재하며, 따라서 1000 dimensional word embedding 을 진행했습니다.
2.
앞서도 언급했지만 input sentence 는 160,000 의 vocabulary 를, output sentences 는 80,000 의 vocabulary 를 사용했습니다.
3.
Deep LSTM 이 Shallow LSTM 보다 학습 효과가 좋았고, 1 layer 의 추가마다 대략 10% 의 perlexity 를 줄일 수 있었습니다.
4.
80000 words 의 naive softmax 를 사용했습니다.
5.
총 384M 의 학습 parameter 가 존재했고, 이 중 64M 이 순수하게 recurrent connection 에 의한 친구들입니다. 32M 이 encoder 에, 남은 32M 이 decoder 에 쓰였습니다.
6.
LSTM 의 학습 parameter 를 -0.08 과 0.08 사이의 uniform distribution 으로 initialize 했습니다.
7.
Optimization Algorithm 으로 SGD 를 사용했으며 momentum 은 적용하지 않았습니다.
8.
0.7 의 고정된 learning rate 를 사용하다가 5 epoch 후에 반으로 줄였고, 총 7.5 epoch 을 학습했습니다.
9.
Batch size 는 128 로 정했습니다.
10.
설계한 모델이 Gradient Vanishing 으로부터는 안전할지 몰라도 Gradient Exploding 으로부터 안전하다는 보장은 없었기 때문에 gradient 의 L2 norm ss 가 5 보다 클 경우에는 gradient gg 를 g=5gsg=\frac{5g}{s} 로 변경하여 적용했습니다.
11.
각기 다른 sentence 들이 각기 다른 길이를 가지기 때문에 batch 로 학습 시에 몇몇 sentence 는 학습이 진행되고 있는데 몇몇은 이미 끝나있어 낭비가 일어났기 때문에 최대한 sentence 길이가 엇비슷한 친구들을 같은 batch 에 배치했으며, 이것으로 학습 효과를 2배 정도 끌어올렸습니다.
12.
위 1~11 까지 중에서 언급했던 configuration 을 사용해 C++ 기반의 Deep LSTM implementation 을 진행했고, single CPU 에서 돌린 결과 1700 words/second 의 프로세싱 능력을 보였습니다. 하지만 이 수치가 논문에서 원하는 바에 한참 미치지 못했기 때문에 8-GPU machine 으로 parallelize 하여 각기 다른 layer 는 다른 GPU 로, 남은 4개의 GPU 는 softmax parallelize 했습니다. 그 결과 모델의 프로세싱 능력이 6300 words/second 로 증가했습니다.
상당히 많은 training detail 을 제공해주었는데 논문에서 어떤 방식으로 성능을 높이는 시도를 했는지에 대해서만 주의 깊게 보고 넘어가시면 좋을 듯 합니다.

Experiment Results

논문에서 진행한 실험에 대한 결과를 이 부분에서 설명해줍니다.
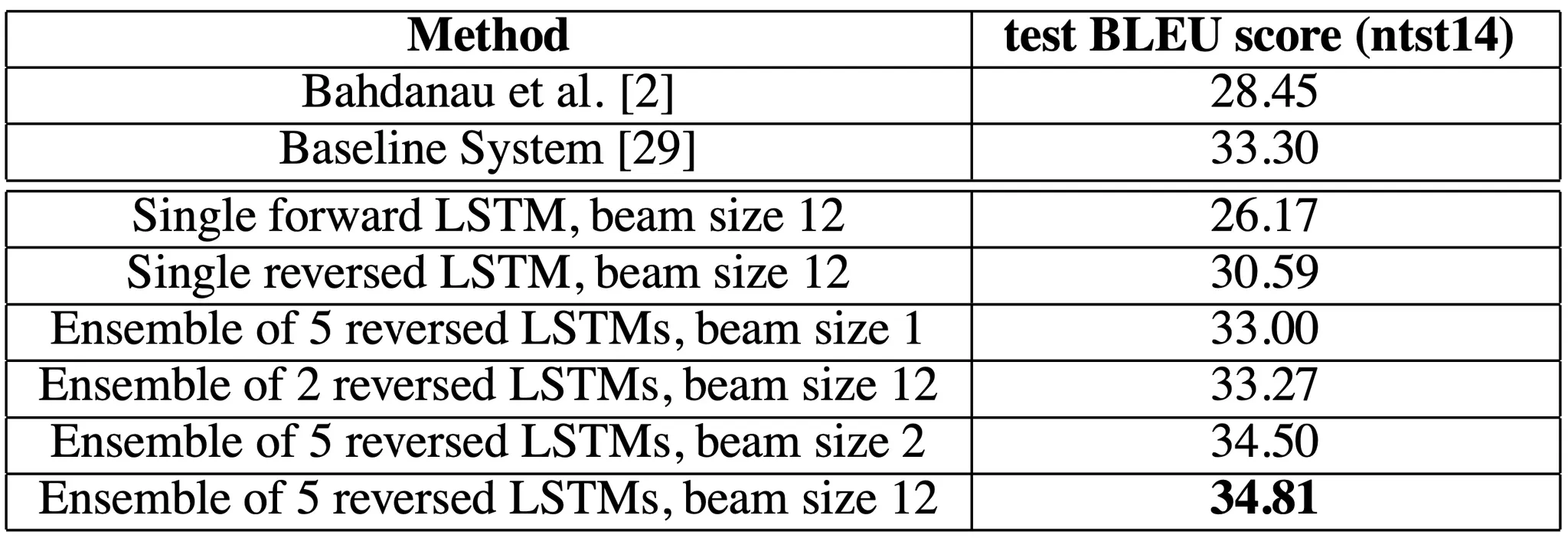
가장 먼저 보여준 것이 위 표입니다. 결론부터 말씀드리자면 기존의 BLEU score 에 비해서 LSTM 을 사용한 논문의 구조가 BLEU score 가 높다는 것을 볼 수 있습니다. 더불어서 LSTM 의 개수가 많은 것이, input sentence forward 보다는 reverse 가, beam size 가 큰 것이 더 좋은 성능을 보였다는 것 또한 케이스별 대조를 통해 알 수 있습니다.
다음으로, SMT based system 에 neural network 를 추가하여 rescoring 했을 때 BLEU score 가 올라가는 것을 확인할 수 있습니다. 비록 Best WMT'14 result 보다 높은 성능을 보여주지는 못했지만, large scale MT 분야에서 phrase-based SMT baseline 를 순수하게 neural translation 으로 뛰어넘은 첫 번째 사례였다는 점에서 의미가 있다고 주장합니다.
다음으로 논문에서는 그들의 모델이 long sentence 에 대한 translation 에도 좋은 성능을 보인다는 것을 정성적으로 보이기 위해 위 표와 같은 예시를 제공합니다. French 를 잘 몰라서 정확히 보기는 어렵지만... 문장이 꽤나 긺에도 어느정도 비슷한 것 같다는 느낌이 듭니다.
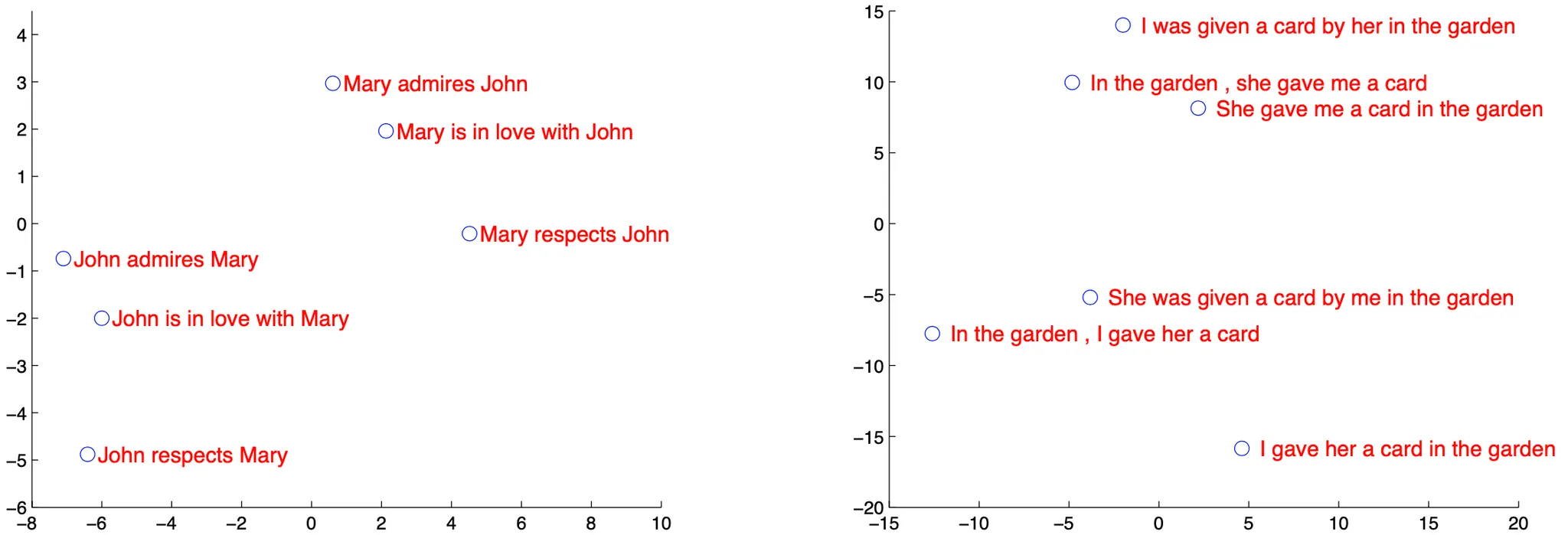
다음으로 논문에서는 학습한 모델에 특정 sentence 를 input 으로 주었을 때 산출되는 hidden state 를 PCA 를 통해서 dimension 을 2차원으로 낮춘 뒤 plotting 한 결과를 보여줍니다. 좌측의 plotting 에서 word 의 순서가 비슷한 문장을 clustering 함을 알 수 있고, 모델의 hidden state 가 word order 에 대한 학습을 진행한 것을 보였습니다. 우측의 plotting 에서는 word 의 순서가 크게 다름에도 의미가 비슷한 문장들 끼리 clustering 함을 알 수 있고, 모델의 hidden state 가 sentence meaning 에 대한 학습을 진행한 것을 보였습니다.
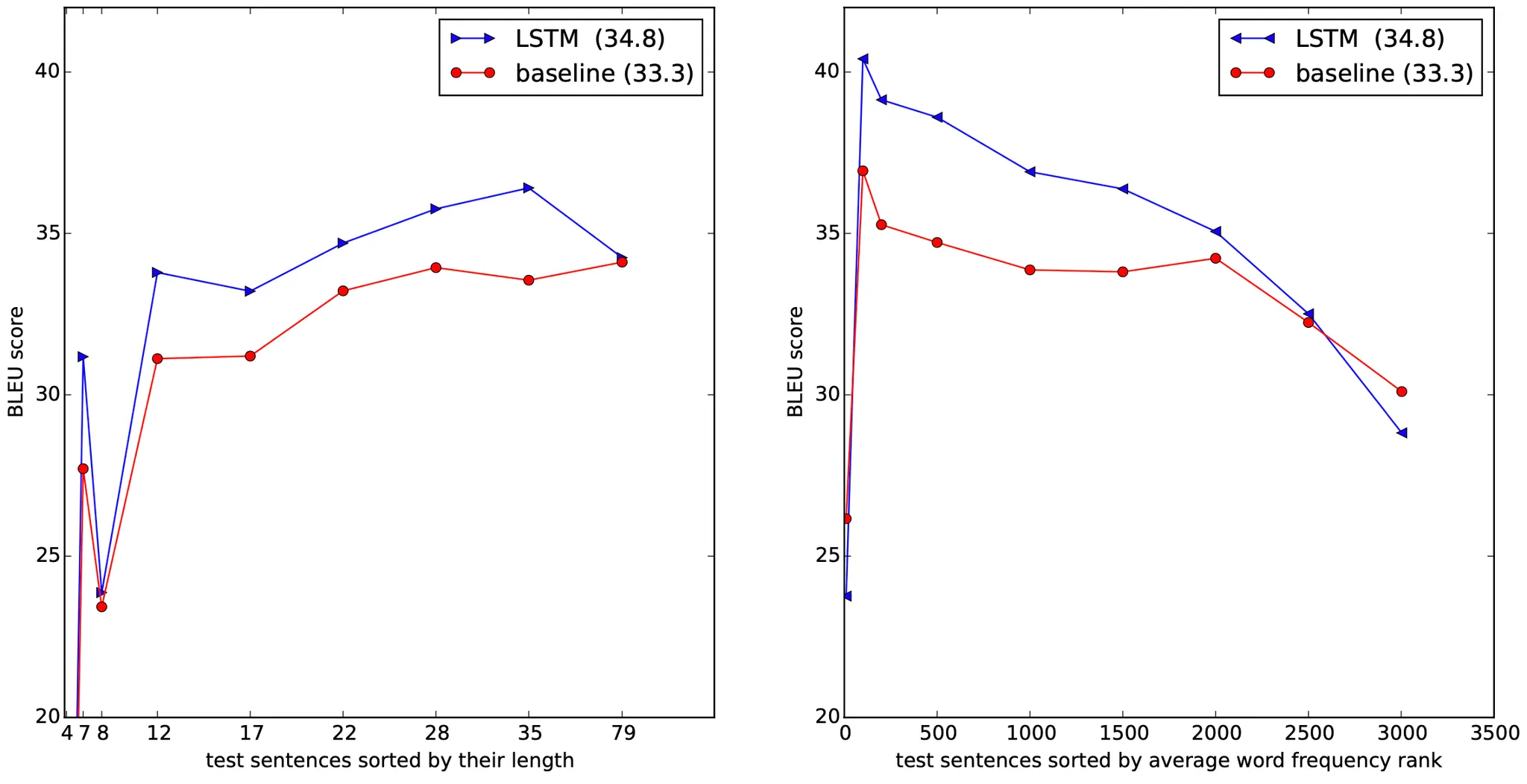
마지막으로 논문에서는 test sentence 의 길이에 따른 LSTM 과 baseline 의 성능 차이를 plotting 한 그래프를 보여줍니다. 좌측의 그래프를 통해서 길이에 따른 성능 저하가 35 words 이하에서는 일어나지 않음을 보였고, 35 words 이후에도 작은 수준임을 언급했으며 전체적으로 LSTM 이 baseline 에 비해서 우세한 성능을 보였습니다. 우측의 그래프를 통해서 자주 사용되지 않는 단어에 대해서도 성능이 기존에 비해 크게 떨어지지 않음은 물론 baseline 보다 높은 성능을 보임을 알 수 있었습니다.

Conclusion

이것으로 논문 “Sequence to Sequence Learning with Neural Networks” 의 내용을 간단하게 요약해보았습니다.
논문에서는 그들의 결론에서 크게 3가지를 언급합니다. 가장 먼저, revesing input sentence 가 높은 성능을 줄지 예측하지 못했었는데 그 발견으로 인해서 short term dependency 를 많이 형성하는 것이 중요하다는 것을 깨달았다고 합니다. 그리고, 메모리에 대한 부족으로 매우 긴 문장에 대해서 좋지 않은 performance 를 보일 것 같았는데 논문 모델이 매우 긴 문장에 대해서도 정확하게 판단했다는 사실이 놀라웠다고 합니다. 마지막으로, 가장 중요하게 언급했던 점은 간단하고 직접적이며 상대적으로 최적화가 되지 않은 모델이었는데도 SMT-based system 을 neural network 만으로 성능 면에서 우위를 점할 수 있었다는 점입니다. 논문에서는 이러한 점이 그들 모델의 의의이자 이후 연구에서 더 좋은 MT 를 할 수 있는 길을 열어주었다고 이야기 합니다.
이전부터 sequential data 에 대한 학습에 궁금증이 많았는데 꽤나 많은 것을 얻을 수 있었던 논문이었던 것 같습니다. 여러분들도 꼭 한 번 읽어보시기를 추천드립니다.