본 세션에서는, Feed Forward (FF) 와는 달리 forward propagation 이 Output Cell 방향이 아닌, Hidden Cell 방향으로도 다시 들어가는 Neural Network 에 대해서 알아보려고 합니다.
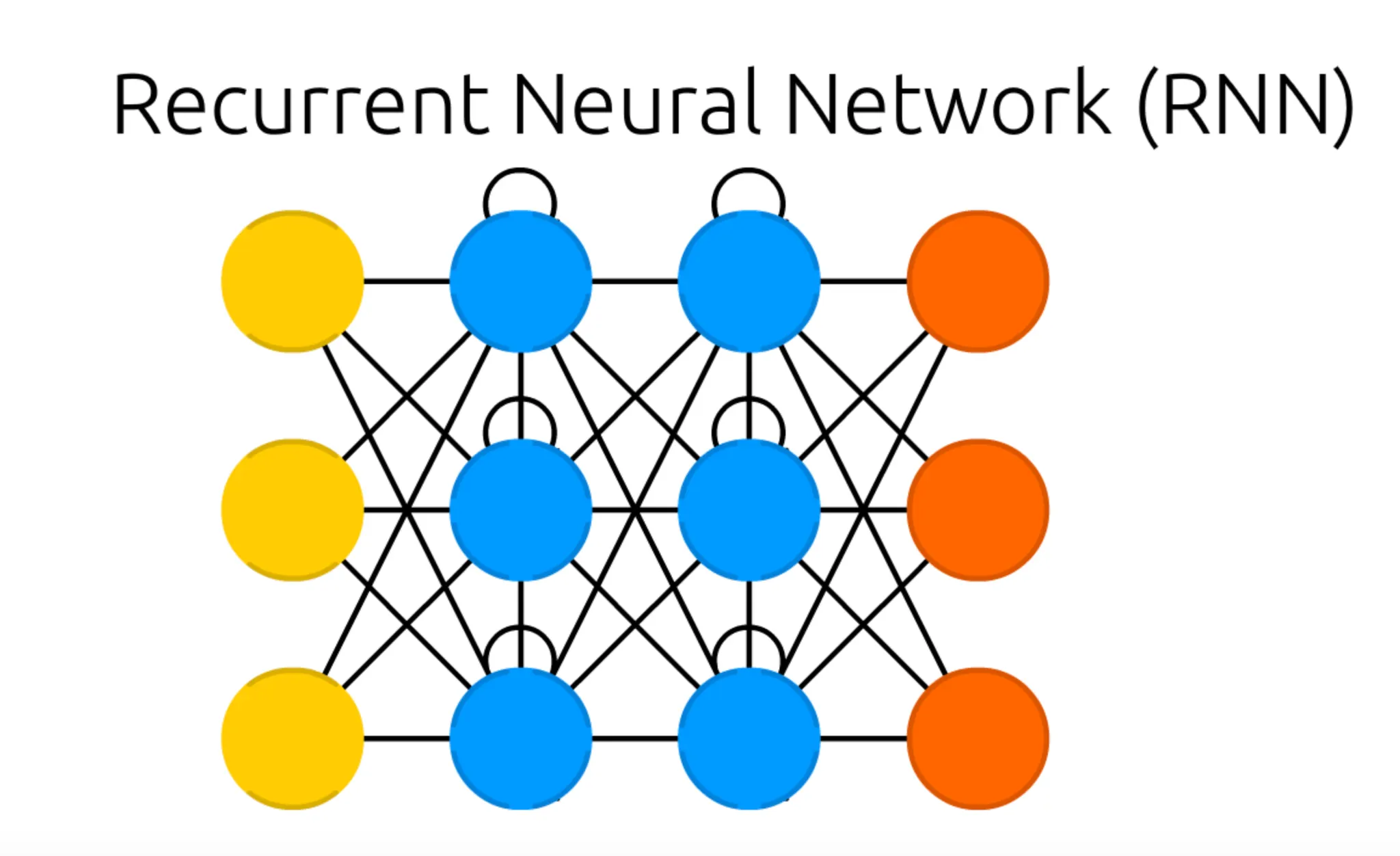
가장 먼저 보이는 구조의 특징적인 변화는 Hidden Cell 이 있던 위치에 자기 자신과 연결된 듯한 선이 있는 Cell 이 대신해 있다는 점입니다. 이러한 형태의 Cell 을 Recurrent Cell 이라고 합니다. 이전과 마찬가지로, Input Cell 과 Output Cell 및 Recurrent Cell 의 개수는 구조와 관련이 없다는 점 알아주시면 좋을 것 같습니다.
그렇다면 Feed Forward (FF) 와 달리 forward propagation 이 output 방향이 아닌 Hidden Cell 방향으로도 다시 들어가는게 갑자기 왜 필요했을까요?
그 이유는, 기존의 Artificial Neural Network 를 가지고서는 시계열(Sequential) 데이터에 기반한 학습을 진행할 수 없었기 때문입니다.
이게 무슨 소리지?... 라고 하실 분들을 위해 간단하게 유명한 예시를 하나 들어보겠습니다.
최근에 네이버에서 공개된 초대형 언어모델인 HyperCLOVA, 그 원작인 CLOVA 를 다들 한 번씩은 들어보신 적 있으실 것입니다.
굉장히 신기하게도, 헤이 클로바- 라는 접두어 이후에 명령어를 말하면 기계가 이를 인식하고 명령어에 해당하는 적절한 답변을 해냅니다. 이렇게 답변을 해낼 수 있는 것은 언어 모델 내부에서 단어 각각에 확률을 할당하여 자연스러운 답변의 단어 뭉치를 구성해내는 것입니다.
여기서 주목해야 할 점은, 단어의 확률을 할당하는 것을 Artificial Neural Network 로 할 수 있다는 것입니다. 그리고 이러한 확률은 대부분, 이전에 온 단어, 혹은 단어들에 영향을 받습니다.
예를 들어, "나는 토요일에 늦게" 라는 단어 뭉치가 있다고 할 때 다음 두 단어 중 어느 것이 뒤에 오기에 적절해 보이시나요?
일어났다.
파랗다.
아마도, 한국어가 모국어인 분들이라면 대부분 1번을 선택하지 않았을까 생각해봅니다. 이렇게 대화 말 뭉치 데이터의 경우에는 단어 각각이 서로와 긴밀한 연결관계를 가지고, 일반적으로는 먼저 오는 단어가 뒤에 오는 단어의 결정에 많은 영향을 줍니다.
그리고 이러한 긴밀한 연결관계처럼 저희가 알 수 없는 복잡한 문제는 보통 Artificial Neural Network 가 큰 힘을 발휘할 수 있는 분야라는 것을 Deep Feed Forward Network 에서도 언급한 적 있습니다. 그런데 기존과 조금 다른 점이 있다면, 기존에 선보였던 Artificial Neural Network 들은 데이터의 선후 관계, 그리고 그 관계로부터 오는 영향을 표현할 수 없었습니다. 이러한 선후 관계와 그 영향을 표현하기 위해 Recurrent Neural Network (RNN) 가 생겨났다고 보시면 됩니다.
그렇다면, 위의 네트워크 구조가 어떻게 데이터의 선후 관계를 표현해줄 수 있는 것일까요?
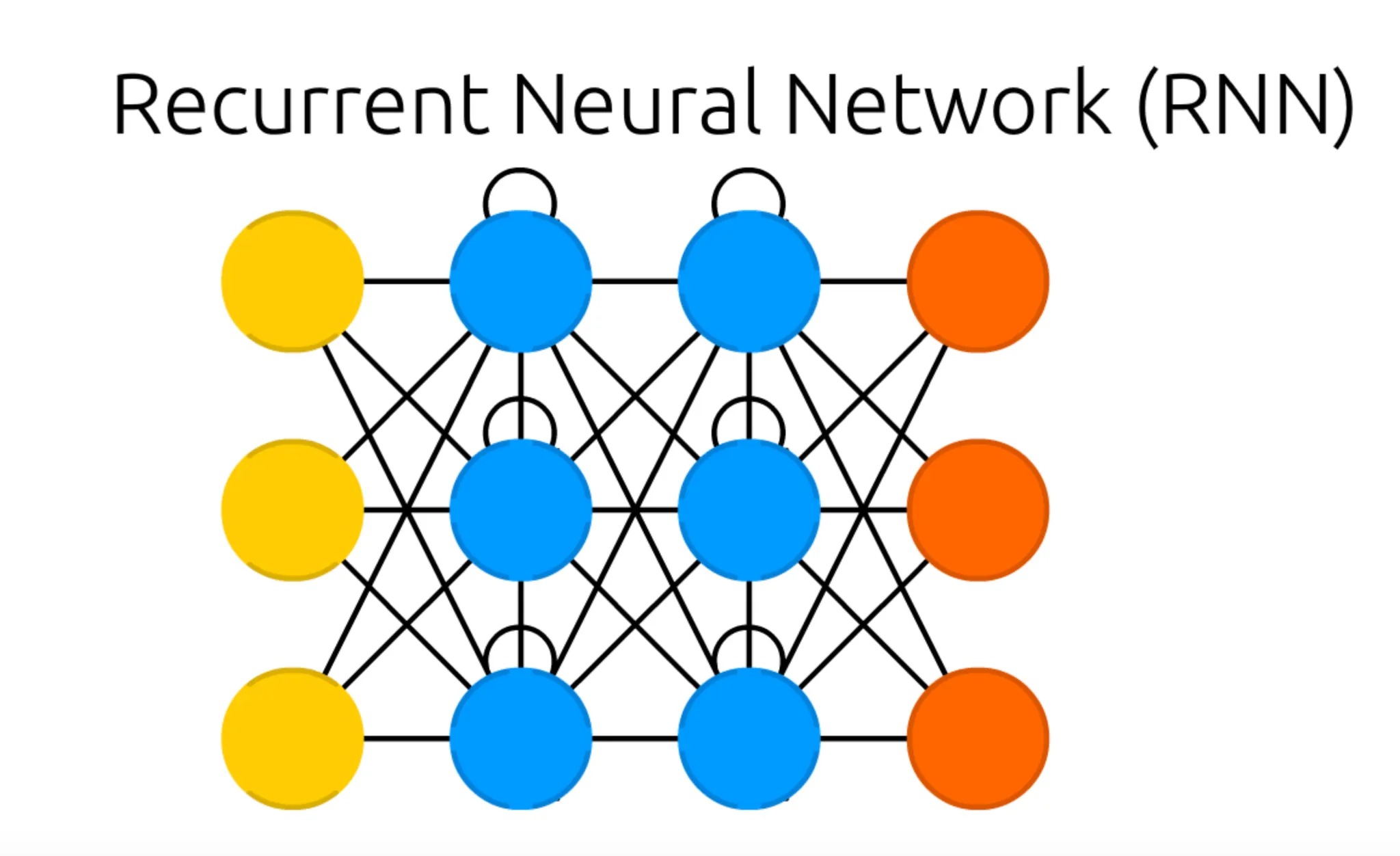
설명의 편의성을 위해 다시 그림을 가져와 보도록 하겠습니다.
사실 위의 그림은, Recurrent Neural Network (RNN) 를 이해하는데 큰 도움을 주지는 않습니다. 이는 위의 그림이 Recurrent Neural Network 의 한 timestamp 에서의 네트워크 구조이기 때문입니다. 여기서 timestamp 란 앞서 이야기한 선후관계의 기준이 되는 단위라 보시면 됩니다. 앞서 설명드린 말 뭉치의 경우에, 첫 번째 단어가 첫 번째 timestamp, 두 번째 단어가 두 번째 timestamp 에 해당하는 것입니다.
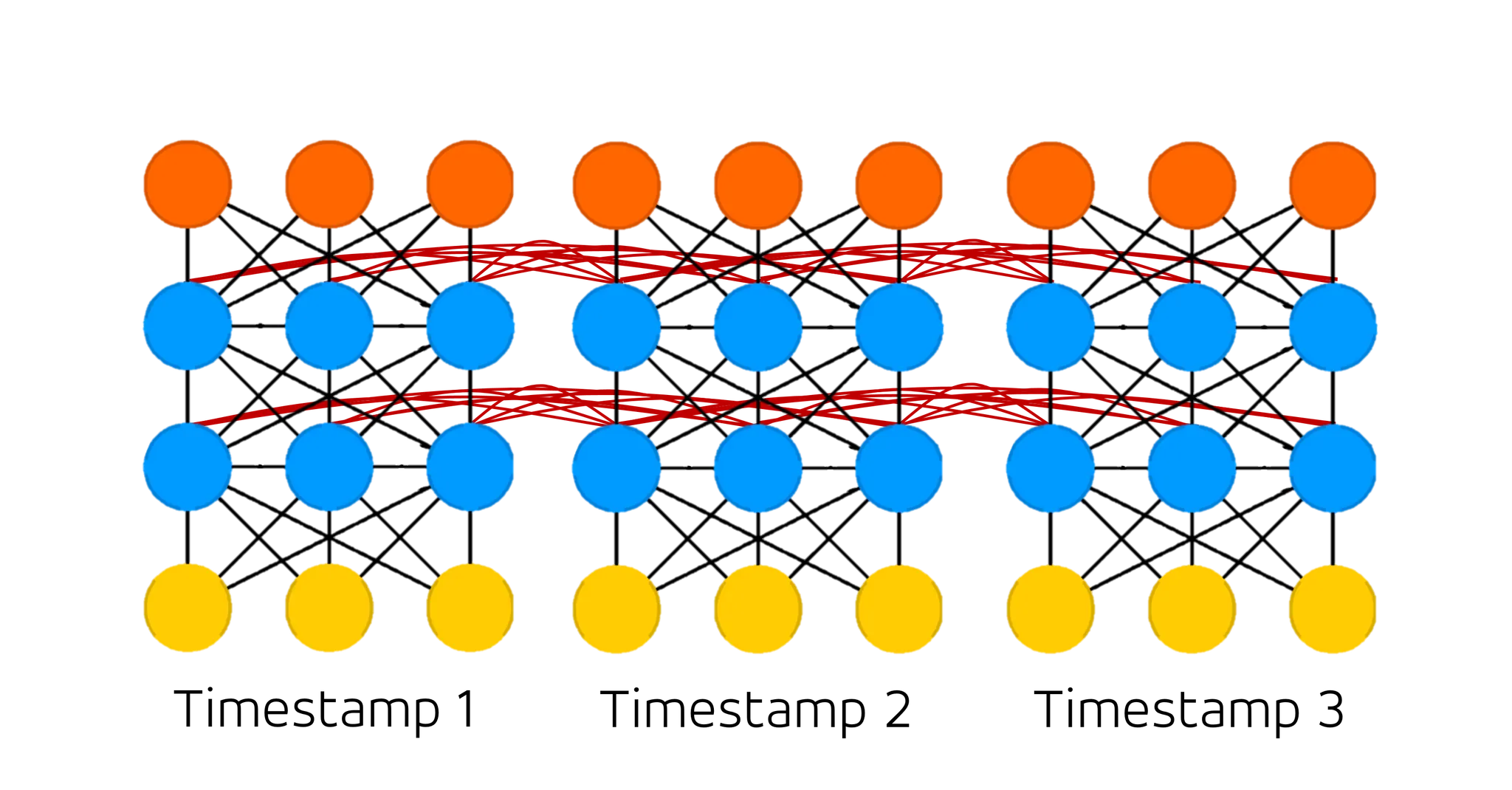
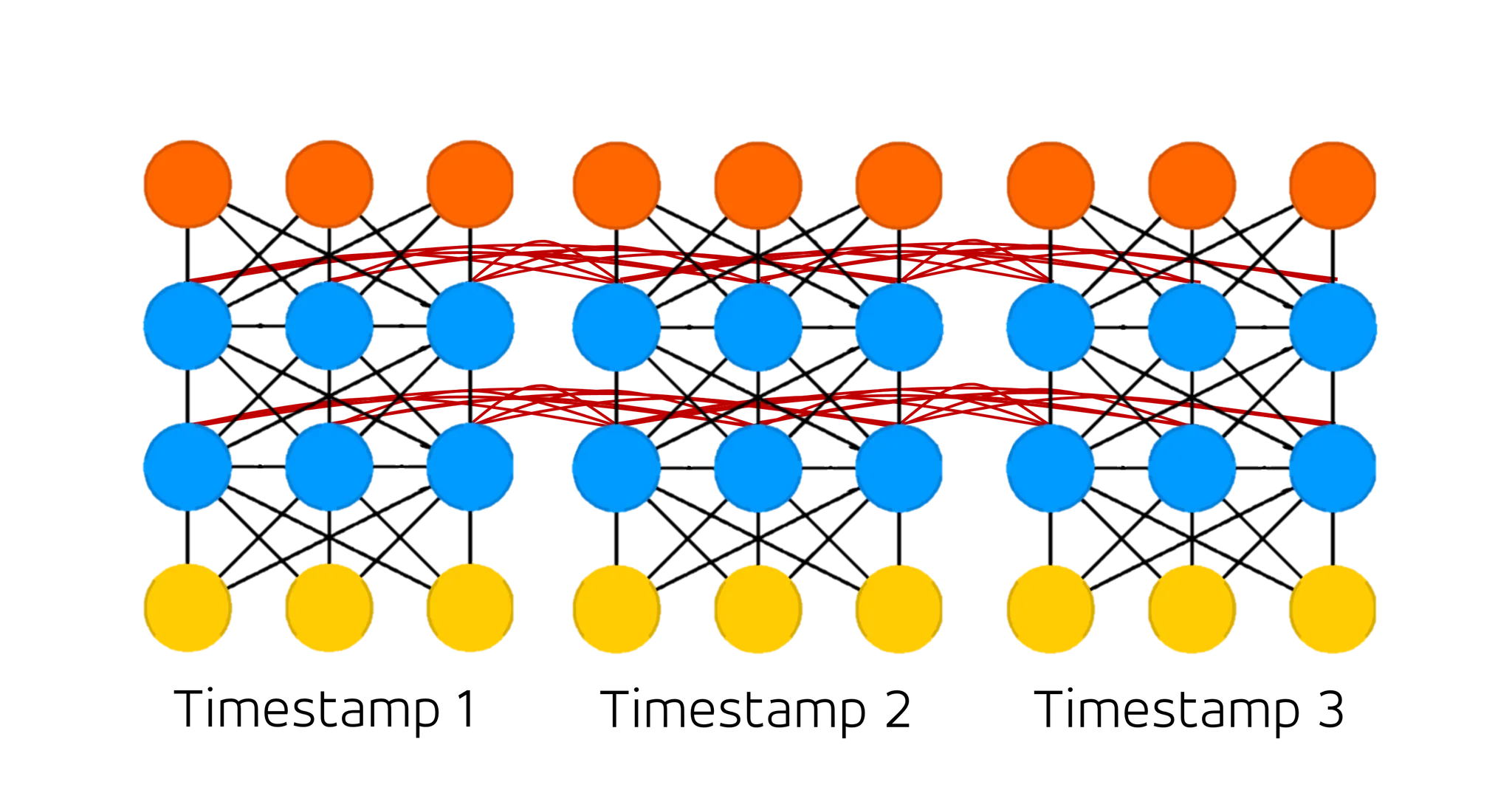
그 timestamp 를 나누어서 실제 네트워크를 표현하게 되면 위와 같은 형태가 나타납니다. 결과적으로 처음 보여드렸던 네트워크의 구조가 압축되어 표현되어 있을 뿐이지 지금 보여드리는 구조와 완벽히 동일하다고 보시면 됩니다. 자세히 살펴보시면, Recurrent Cell 에 존재했던, 자기 자신에게 이어졌던 연결관계가 사라지고 다음 timestamp 의 Hidden Cell 과의 연결관계(붉은 선)가 생긴 것을 보실 수 있습니다. 이것이 Recurrent Neural Network (RNN) 에서 선후관계를 나타내는 방법입니다. 다시 말 뭉치의 예시를 들자면, 위의 그림에서 각 timestamp 의 Input Cell 과 Output Cell 은 vectorized 된 단어 하나로 보실 수 있습니다.
그렇다면, 구체적으로 모델의 연산은 어떻게 될까요?
이는 굳이 설명드리지 않아도 될 정도로 간단합니다. 기존의 Artificial Neural Network 들에서 그랬던 것처럼, 여기서도 Cell 에 연결된 선들을 기준으로 Sum of Product 를 진행합니다. 즉, 특정 Cell 의 값을 계산하고 싶다면, 그것과 연결된 이전 Cell 들의 출력 값에 선의 값을 곱한 것을 전부 더하면 된다는 뜻입니다. 물론, 더하고 나서 activation function 을 거치는 것도 잊지는 말아야겠죠!
앞선 네트워크에 대한 설명해서 하나의 layer 가 나타내는 연산이 형태임을 말씀드린 적 있습니다. 이를 이용해서 timestamp 2 의 첫 번째 Hidden Layer 의 값을 구하는 연산을 정의해보면 다음과 같습니다.
일반적으로, 위의 식처럼 Hidden Layer 의 값을 로 정의하며 (여기서는 Hidden Layer 가 2개이기 때문에 등으로 나타낼 수 있을 것 같네요), 은 첫 번째 Hidden Layer 에서 다음 timestamp 로의 connection 에 해당하는 weight 입니다. 은 (Input Cell 에서의) 첫 번째 Hidden layer 로의 connection 에 해당하는 weight 입니다.
그리고, 가 Hidden Layer 의 값이기도 하지만 각 timestamp 에서 Output Cell 로 뽑아낼 특성을 가지고 있는 Hidden State 이기도 합니다. Hidden State 로부터 Output 을 출력해내는 연산은 다음과 같습니다.
여기까지 오시면 Recurrnet Neural Network 의 구조에 대해서 다 이해한 것입니다. 하지만, 이 시점에 많이 햇갈리는 사항에 대해서 간단히만 짚고 넘어가려고 합니다.
다시, 이 그림을 가져왔습니다. 여기서 weight 가 각각의 선인 것은 알고 계실 것입니다. 다만 그림에서 선들이 서로 따로 그려진 것과는 달리 각 timestamp 에서 연결된 선들은 timestamp 와 상관없이 weight 를 공유합니다. 이는 실제로 길이가 일정하지 않은 시계열 데이터들을 학습해야하기 때문라고 보시면 됩니다. 각 timestamp 마다 weight 를 공유하지 않으면 길이가 5 인 말뭉치가 들어왔을 때는 weight 를 5 뭉치를 initialize 해야하고, 또 길이가 7 인 말뭉치가 들어왔을 때는 weight 를 7 뭉치를 initialize 해야 하는데 이러다 보면 현실적으로 가장 긴 말뭉치에 대한 학습을 지원하기 위해 굉장히 많은 메모리를 할당해야 하기 때문입니다. 물론, 불가능하다! 는 아니지만, 일반적으로는 그렇게 진행하지 않는다는 점 알아주시면 좋을 것 같습니다.
이쯤에서, 궁금하실 수도 있는 점 한 가지만 언급하고 마무리하도록 하겠습니다.
일반적으로 activation function 하면, ReLU 가 zero-centered problem 과 gradient vanishing problem 을 어느정도 완화해주기 때문에 좋다고 알려져 있는데, Recurrent Neural Network 에서는 를 사용했습니다. 그 이유가 무엇일까요?
그 이유는 Recurrent Neural Network 가 weight 를 공유하는, 반복되는 구조를 가지고 있기 때문입니다. 앞서 말씀드린 것처럼 데이터의 길이가 다양하기 때문에 그 길이에 따라 굉장히 많은 activation 을 거치는데, 양의 범위에서 크게 발산하는 ReLU 의 특성상 numerical problem 이 나타날 수 있기 때문입니다.
아마, Computer Vision 에 관심이 있으신 분들은 "그럼 Batch Normalization 을 ReLU 와 함께 채용하면 되지 않아?" 라고 이야기하실 수도 있을 것입니다. 저도 처음에 이러한 궁금증을 가지고 있었지만, 이내 Recurrent Neural Network 에서의 weight 는 공유가 되고, 각 timestamp 별로 statistic 한 distribution 을 제약하는 constraint 를 둘 수 없기 때문에 이러한 방법이 가능하지 않다고 합니다.
이제 위의 궁금증이 해결되었으리라 믿습니다. 
이렇게 이번 세션에서는 시계열 데이터를 기반으로 학습을 진행할 수 있도록 내부에 선후관계를 구현한 네트워크인 Recurrent Neural Network (RNN) 에 대해서 알아보는 시간을 가졌습니다. 이번 세션을 통해서 Recurrent Neural Network (RNN) 이 어떤 task 에 사용되는지, 그리고 어떠한 구조를 가지고 있는지에 대해서 알아두시면 좋을 것 같습니다.