Lecture 6 | Training Neural Networks (1)

포스팅 날짜

2021/08/12

지난 강의 보기 - Lecture 5 | Convolutional Neural Networks

다음 강의 보기 - Lecture 7 | Training Neural Networks (2)

Note Taking

Lecture 5 요약

•

Fully-Connected Layer

◦

연산 자체는 Matrix Multiplication 과 동일

◦

1 dimension vector input (N×1N\times 1N×1)

◦

1 dimension vector output (M×1M\times1M×1)

◦

2 dimension vector weight (M×NM\times NM×N)

◦

Convolutional Neural Network 에서 마지막에 최종 output 을 산출하기 전에 모든 feature 와 연결된 새로운 vector 를 만들기 위한 layer

•

Convolution Layer

◦

Image, 혹은 2(or 3 with depth) dimension vector 의 spatial dimension 을 유지하는 연산

◦

Input vector (N×N×dN\times N \times dN×N×d)

◦

Input 을 convolving 하는 filter (== kernel == receptive field) 정의 (F×F×dF\times F \times dF×F×d)

◦

Filter 가 input vector 를 convlove 하며 dot product 연산을 하고, input vector 와 spatial dimension 이 같은(혹은 size 가 변하긴 하지만 형태 유지) output vector 를 출력해냄

◦

Filter 의 개수 kkk

◦

Filter 가 convolving 하는 간격 stride sss

◦

Input 의 가장자리에 붙는 padding ppp

◦

Output vector ([(N−F+2×p)/s+1]×[(N−F+2×p)/s+1]×k[(N-F+2\times p)/s +1]\times[(N-F+2\times p)/s +1]\times k[(N−F+2×p)/s+1]×[(N−F+2×p)/s+1]×k)

◦

Image 내에서 지역적인 특성을 추출해 내기 위한 layer

•

Pooling Layer

◦

Image, 혹은 2(or 3 with depth) dimension vector 의 spatial dimension 만을 줄이는 연산

◦

Convolution Layer 에서 padding, filter 개수 개념만 제외

◦

Output vector depth 는 Input vector depth 와 동일

◦

Filter 가 input vector 를 convolve 하며 특정한 연산(ex. max) 을 통해 대표 값 하나를 산출하여 input vector 에서 size 가 줄어든 output vector 를 출력해냄

◦

Output vector([(N−F)/s+1]×[(N−F+)/s+1]×d[(N-F)/s +1]\times[(N-F+)/s +1]\times d[(N−F)/s+1]×[(N−F+)/s+1]×d)

Mini-batch SGD

•

Training data 중 일부를 batch 로 묶어 sampling

•

Network 를 통해 forward propagation

•

Back Propagation 을 통해 weight-wise gradient 계산

•

Gradient 를 사용해 weight update

Activation Functions

•

Input vector 와 Weight 와의 연산 이후에 non-linearity 를 부여

•

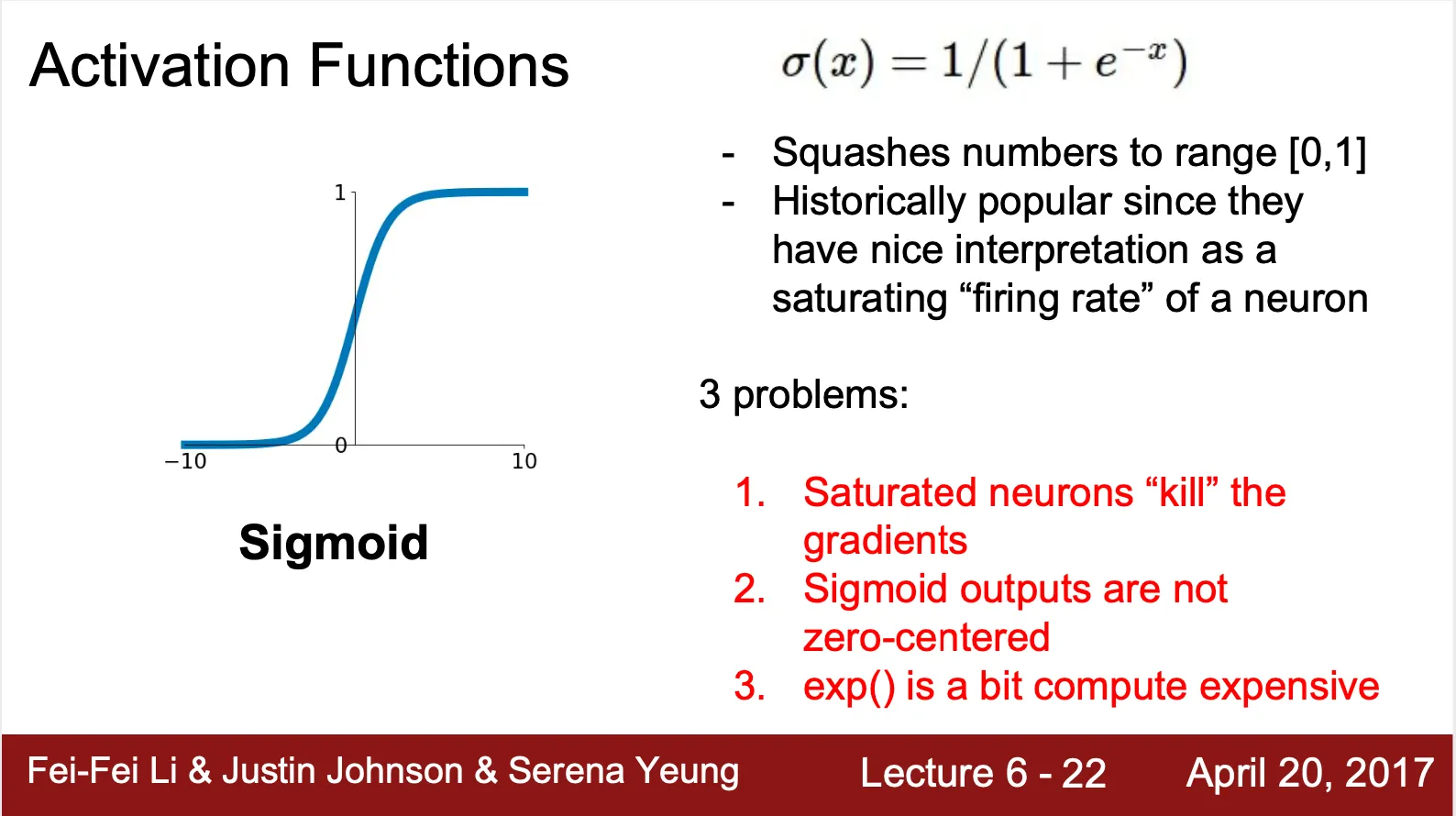
Sigmoid ?

◦

일정 수준 이상이 되면 자극이 전달되는, 생물학적 neuron 의 "firing rate" 를 잘 묘사했다는 전통적인 평가를 받으며 자주 사용되던 activation function

◦

모든 값을 [0,1][0,1][0,1] 사이로 mapping

◦

σ(x)=11+e−x\sigma(x) = \frac{1}{1+e^{-x}}σ(x)=1+e−x1​

•

세 가지 문제점이 존재

◦

Saturated 된 neuron 은 gradient 를 더 이상 전달하지 않음

▪

Downstream gradient 는 Upstream gradient 와 local gradient 의 곱 연산(Chain Rule)

▪

Local gradient 가 0 에 가까이 수렴하기 때문에 downstream gradient 가 사라짐

◦

Exponential 이 꽤나 비싼 연산임 (Convolution 이 더 비싸서 딱히 유의미하진 않음)

◦

Zero-Centered 되어 있지 않음

▪

Input X 의 모든 요소가 양수라면?

•

Local gradient 는 x 의 각 요소이기 때문에 무조건 양수

•

Downstream gradient 의 경우에는 요소에 상관 없이 무조건 양수 혹은 무조건 음수 (Upstream gradient 가 양수면 양수로, 음수면 음수로 결정)

•

Gradient update 의 방향성이 제한되어 버림 + 수렴 속도도 느려짐

•

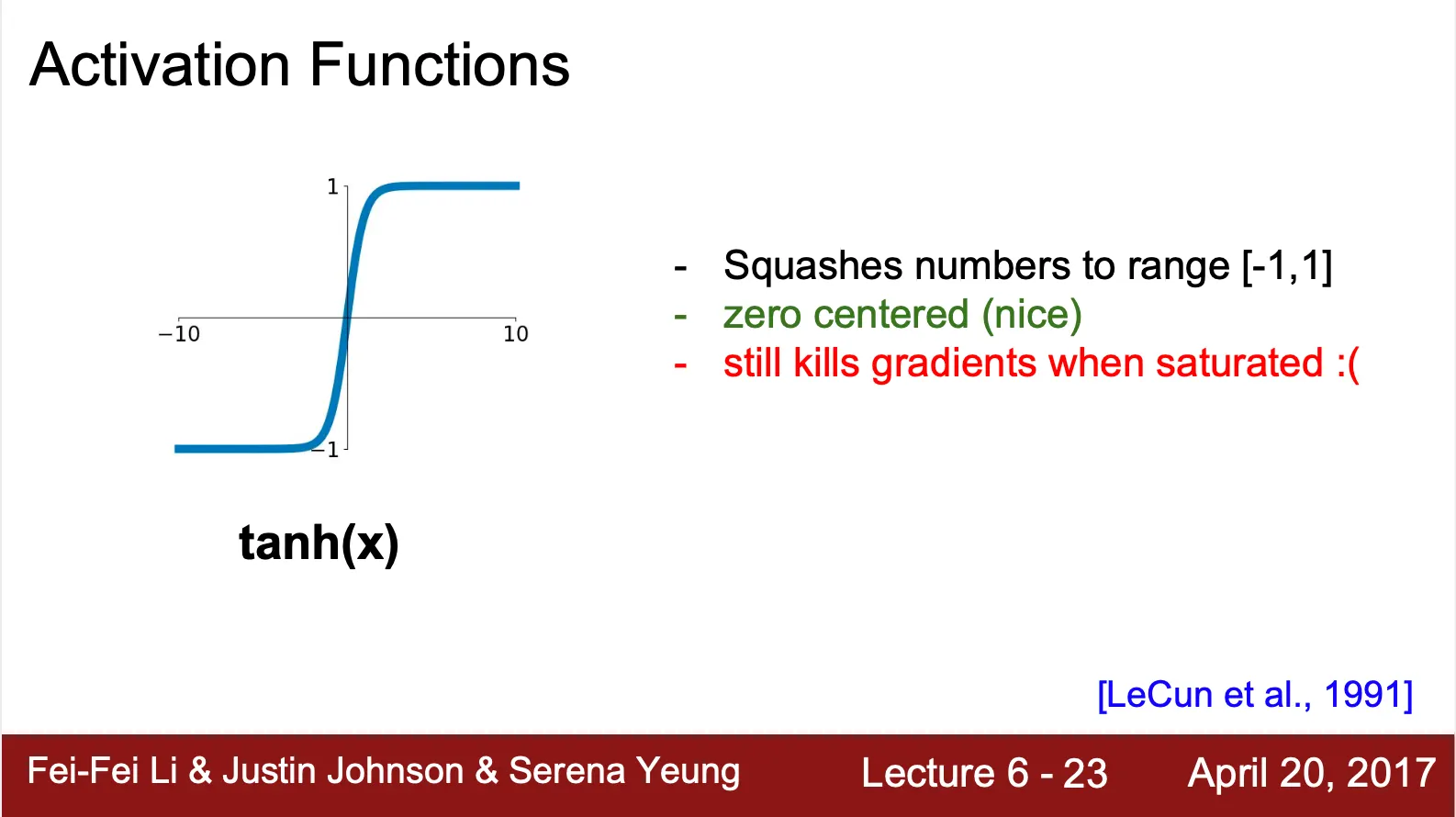
tanh (Hyper Tangent)?

◦

Sigmoid 에서 나타난 Not Zero-Centered 문제를 해결한 활성화 함수

◦

모든 값을 [−1,1][-1,1][−1,1] 사이로 mapping

◦

여전히 saturation 시 gradient 를 없애는 문제가 존재

•

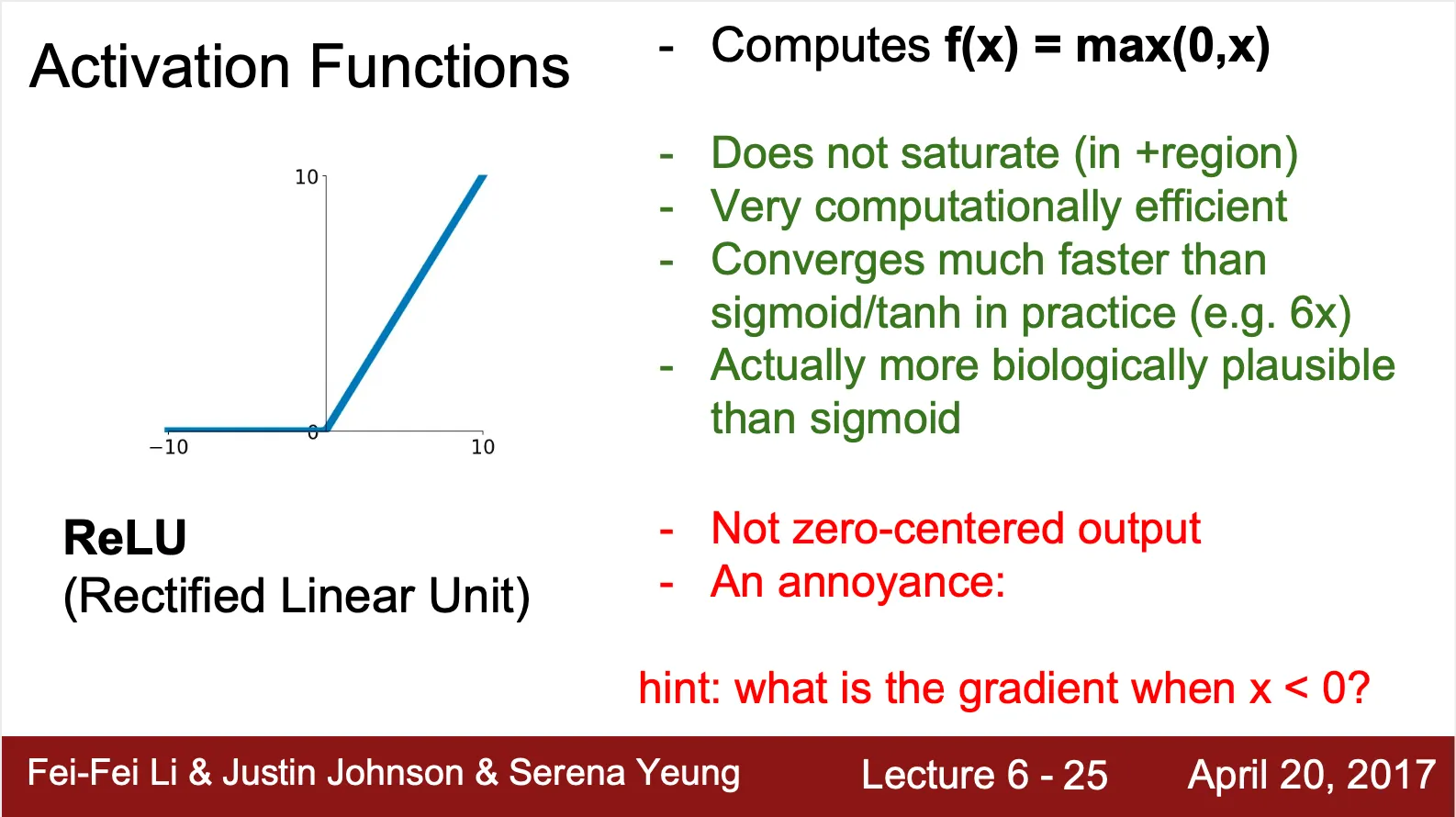
ReLU (Rectified Linear Unit) ?

◦

Sigmoid 의 단점을 보완하면서도 생물학적으로 더 좋은 근사함수로 제시된 활성화 함수

◦

ReLU(x)=max⁡(0,x)\rm{ReLU(\it{x})} =\max(0,\it{x})ReLU(x)=max(0,x)

◦

Sigmoid 의 saturation 문제를 해결 (positive region 에 대해)

◦

Negative region 에 대해서는 여전히 saturated (dead ReLU)

▪

Negative region 에 대해서 0 을 산출하여 neuron 의 활성도가 0 이 된 이후 network 에 영향을 줄 수 없음 

▪

이후 network 에 대한 영향이 없기 때문에 upstream gradient 가 0 이 됨

▪

Upstream gradient 가 0 이기 때문에 downstream gradient 도 0 이 되고 weight update 가 일어나지 않음 (dead ReLU)

◦

여전히 Not Zero-Centered

•

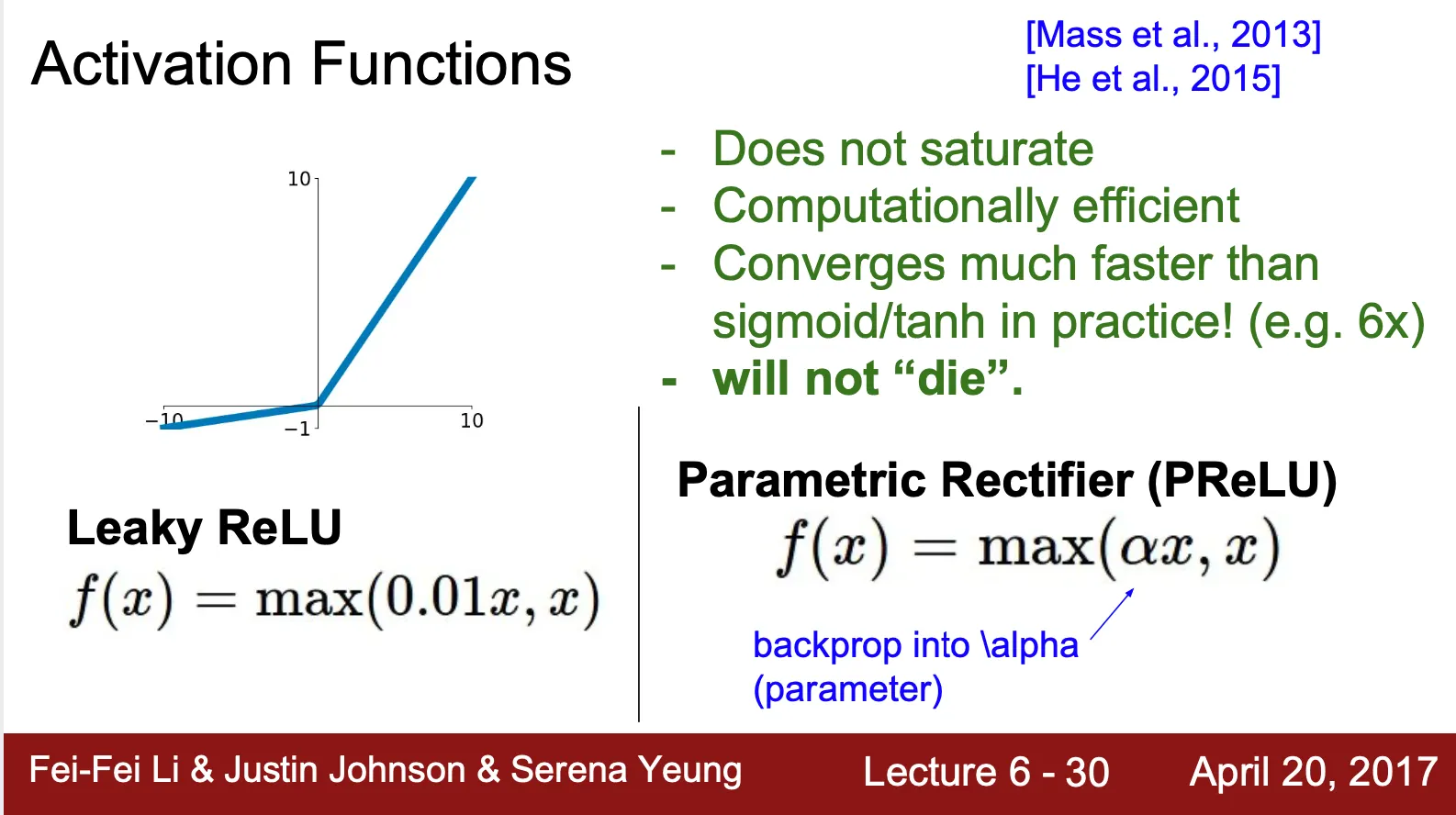
Leaky ReLU & Parametric ReLU?

◦

ReLU 에서 나타난 dead ReLU 문제를 해결하기 위해 제시된 활성화 함수

◦

Leaky ReLU=max⁡(0.01x,x)\rm{Leaky\ ReLU} =\max(0.01 \it{x}, x)Leaky ReLU=max(0.01x,x)

◦

Parametric ReLU=max⁡(αx,x)\rm{Parametric\ ReLU} =\max(\alpha \it{x}, x)Parametric ReLU=max(αx,x), α<1\alpha < 1α<1 는 constant

◦

Saturation 문제를 all region 에 대해서 해결

◦

Zero-Centered (음수를 산출하는 영역 존재)

•

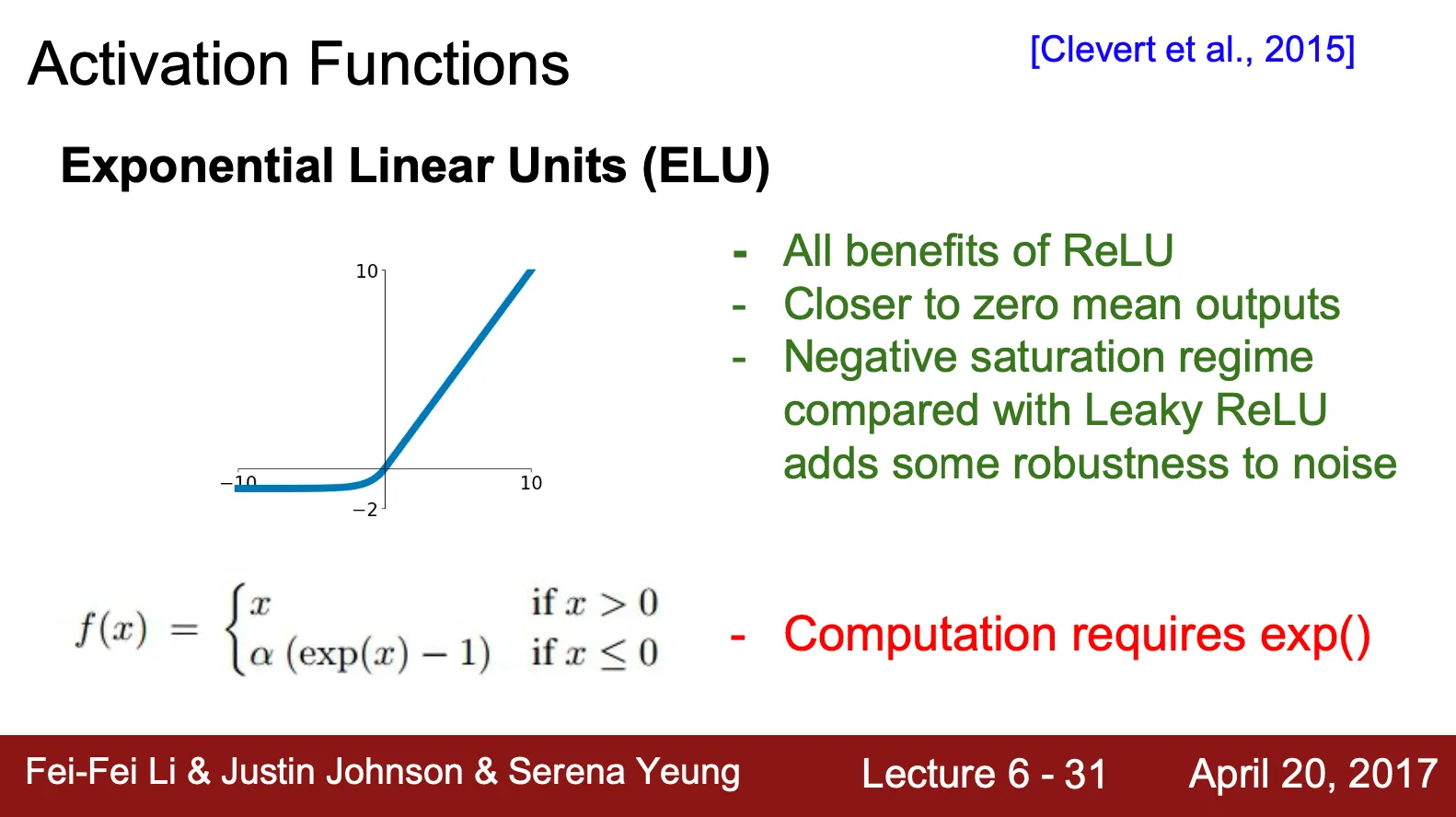
ELU (Exponential Linear Unit) ?

◦

ReLU 의 변종 중 하나

◦

ELU={xif x>0α(ex−1)if x≤0\rm{ELU}=
\begin{cases}
x & \rm{if\ } {x>0} \\
\alpha(e^x-1) & \rm{if\ } {x\le0}
\end{cases}ELU={xα(ex−1)​if x>0if x≤0​

◦

ReLU 의 장점들을 모두 가지고 있음

◦

Leaky ReLU 나 Parametric ReLU 랑은 달리 negative region 에서 saturation 을 보임

▪

단점일 수 있으나, noise 에 robust 하다는 장점을 가짐

◦

ReLU 와 Leaky ReLU 의 중간형으로 볼 수 있음

▪

ReLU 보다는 Zero-Centered

▪

Leaky ReLU 보다는 Saturated

•

Maxout ?

◦

Activation Function 이라기 보단 Non-Linearity 를 부여할 수 있는 Layer

◦

max⁡(W1Tx+b1,W2T+b2)\max(W_1^Tx+b_1,W_2^T+b_2)max(W1T​x+b1​,W2T​+b2​)

◦

ReLU 에서는 0 과 한  weight 연산 결과(WTx+bW^Tx+bWTx+b) 사이를 max⁡\maxmax 를 했다면, 여기는 두 weight 연산 결과 사이를 max⁡\maxmax 연산을 취함 

Data Preprocessing

•

앞서 언급했던, 데이터가 Not Zero-Centered 시 나타나는 문제점(specific direction update) 해결 

•

Standard Data Preprocessing

◦

Zero-Mean

◦

Normalization

•

Machine Learning Preprocessing

◦

PCA (데이터를 표현하는 vector space 의 주성분을 추출하여 새롭게 데이터를 표현)

◦

Whitening (모든 variable 을 uncorrelated 하게 바꾸며 variance 를 1로 만드는 과정)

Weight Initialization

•

네트워크 학습 시의 초기 weight 를 initialize 하는 방법론

•

Zero Initialization

◦

W=0W=0W=0

◦

모든 값을 0 으로 초기화

◦

일반적인 네트워크에서 각 neuron 의 연결 관계가 symmetric 하기 때문에 동일한 양상으로 update 가 진행되어 좋지 않음

◦

bias 나 non-linearity 때문에 neuron 의 update 가 안 일어나지는 않음

•

Small Standard Normal Initialization

◦

W=0.01×N(0,1)W=0.01\times\cal{N}{\rm(0,1)}W=0.01×N(0,1)

◦

작은 네트워크에서는 괜찮으나, 큰 네트워크에서 activation 이 0 으로 수렴하게 됨

▪

WTx+bW^Tx+bWTx+b 값이 작아지고 tanh⁡\tanhtanh 를 거치면서 0 에 가까워지는 구조

▪

각 layer 의 activation 의 standard deviation 이 점점 감소해 0 이 되어버림

▪

설상가상으로, activation 이 0 에 가까워지면 앞서 살펴본 것처럼 update 도 일어나지 않게 됨

•

Big Standard Normal Initialization

◦

W=1.0×N(0,1)W=1.0\times\rm{\cal{N}\rm(0,1)}W=1.0×N(0,1)

◦

모든 neuron 이 saturated 됨

▪

WTx+bW^Tx+bWTx+b 값이 커지고 tanh⁡\tanhtanh 를 거치면서 양 극단에 가까워지는 구조

▪

각 layer 의 activation 이 -1 또는 1 이 되어버림

▪

Saturation 문제 때문에 update 가 일어나지 않게 됨

•

Xavier Initialization 

◦

위 두 경우의 normal initialization 에서 나타난 문제를 해결하기 위해 제시된 초기화 방법

◦

W=1#fan−in×N(0,1)W=\sqrt{\frac{1}{\rm{\# fan- in}}}\times\cal{N}\rm{(0,1)}W=#fan−in1​​×N(0,1) (논문과의 식이 다른데, 강의에서 약식으로 가져온 듯 함)

◦

#fan−in\#\rm{fan-in}#fan−in 이 커지면, 전체적인 WTx+bW^Tx+bWTx+b  값이 커질 것을 생각하여 weight 를 작게 하려하고, #fan−in\#\rm{fan-in}#fan−in 이 작아지면, 전체적인 WTx+bW^Tx+bWTx+b  값이 작아질 것을 생각하여 weight 를 크게 하려함

◦

요점은, WTx+bW^Tx+bWTx+b 값이 너무 작지도, 너무 크지도 않게 나오게 하는 것

◦

Activation 의 분포가 layer 를 지나도 normal distribution 을 유지하려고 함

◦

ReLU 를 사용할 경우 반 정도의 activation 을 0 으로 만들어버리기 때문에 전체적으로 WWW 가 작아지는 경향성을 더 많이 가졌음

•

He Initialization

◦

Xavier Initialization 에서 ReLU 를 사용할 경우 나타났던 문제를 해결하기 위해 제시된 초기화 방법

◦

W=2#fan−in×N(0,1)W=\sqrt{\frac{2}{\rm{\# fan- in}}}\times\cal{N}\rm{(0,1)}W=#fan−in2​​×N(0,1) (논문과의 식이 다른데, 강의에서 약식으로 가져온 듯 함)

◦

반 정도의 neuron 이 0 으로 산출된다는 점에 착안하여 WWW 의 크기를 일부 늘려줌 (0 이 되는 neuron 의 수의 감소)

Batch Normalization

•

앞에서 Activation 의 분포가 layer 를 지나도 normal distribution 이 유지되기를 원함 (Update 중간에 distribution 이 보통 0, -1, 1 등의 값으로 수렴하여 제대로 된 update 가 일어나지 않았기 때문)

•

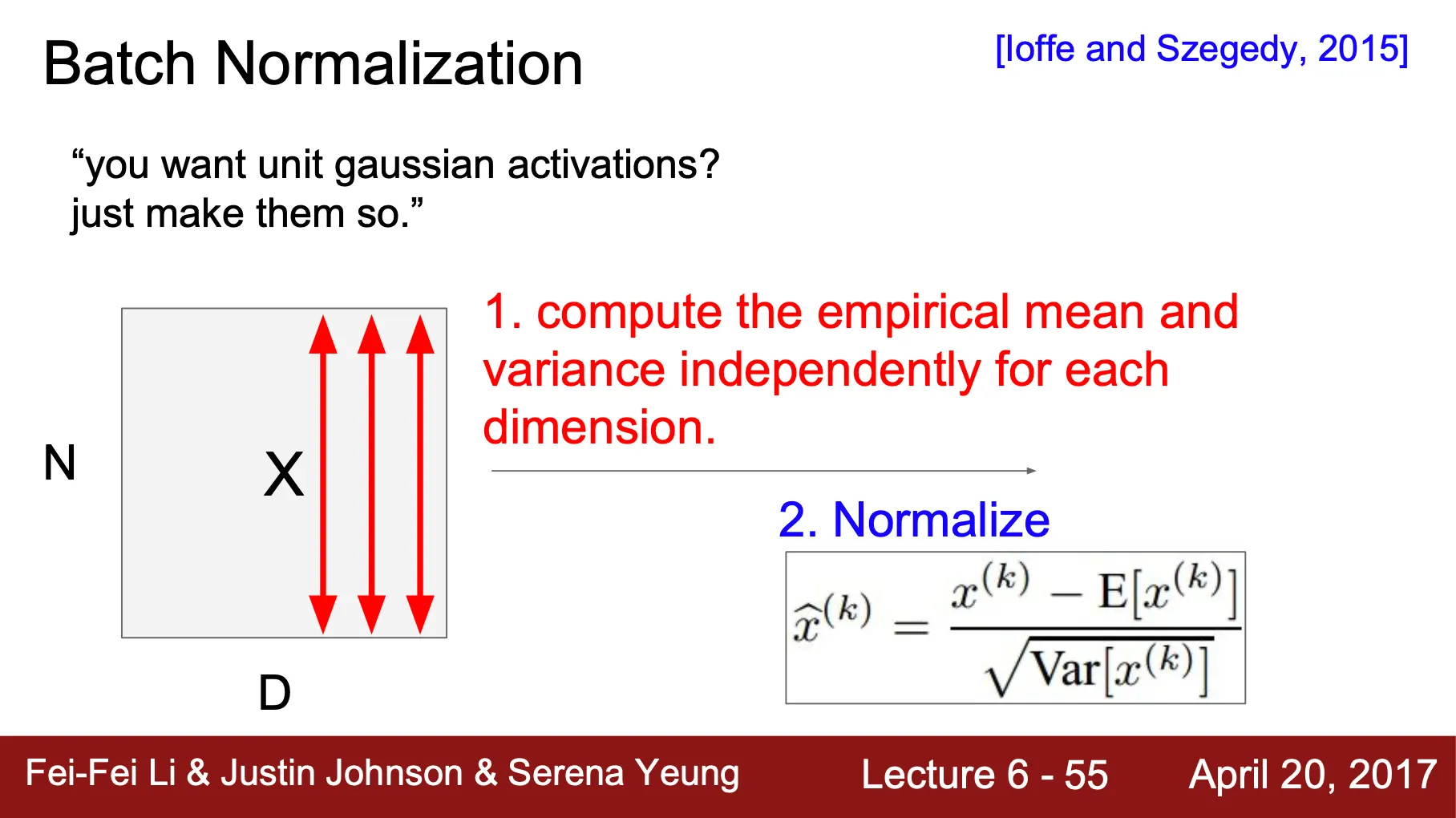
"Activation 이 normal distribution 이 되기를 원한다면, 매번 그렇게 바꾸어주면 되잖아 ?"

•

Batch 에 속하는 vector 들 사이의 mean 과 variance 를 training time 에 계산하여 normalize

•

보통, Batch Normalization Layer 는 Fully Connected Layer 와 Convolution Layer 이후에 옴

•

Normal distribution 으로의 data 를 강제하는 것이 항상 좋다는 확신이 없기 때문에 parameter 를 도입하여 flexibility 를 부여

◦

γ\gamma γ for scaling

◦

β\betaβ for shifting

Babysitting the Learning Process

•

Preprocess the data

•

Choose the architecture

•

Double check that the loss is reasonable

◦

첫 시작 시 loss 가 합리적인 수치인지 검증 (softmax 일 경우, cross entropy 를 쓸 것이므로 −log⁡(1#classes)-\log(\frac{1}{\#\rm{classes}})−log(#classes1​))

◦

Regularization 을 추가했을 때 regualriazation loss 가 추가되는 것을 확인

◦

적은 dataset 으로 먼저 학습을 진행해보고 overfitting 을 할 수 있는지 확인 (loss 가 zero-toward 될 수 있는지) 

◦

Regularization 을 작게 유지한 채 좋은 learning rate 를 rough 하게 찾음

▪

큰 learning rate 를 사용하면, loss 가 Not a Number 가 등장할 수 있음 (loss exploding)

▪

Loss 는 비슷해도 accuracy 가 좋아지는 경우는 어떻게 설명할까?

•

Loss 의 각 요소 (softmax 시 각 class 에 해당하는 값들) 이 shifting 되면서 top-1 class probability 가 ground-truth 인 경우가 많아진 것임

Hyperparameter Optimization

•

좋은 hyperparameter 를 어떻게 얻을까 ?

◦

Coarse → Fine Cross-Validation

▪

짧은 학습으로 대략적인 좋은 hyperparameter 의 범위를 찾음 (Coarse Serach)

▪

긴 학습으로 좋은 hyperparameter 를 정확하게 찾음 (Fine Search)

▪

Original loss 의 3 배 이상 loss 가 커지는 현상을 목격한다면 Loss Explosion 으로 봐도 됨

▪

Fine Search 에서 best case 가 범위의 끝 부분에 나타난다면, 범위를 늘려서 확인해보는 것이 좋음 (실제로 optimal case 가 아닐 가능성이 있기 때문)

•

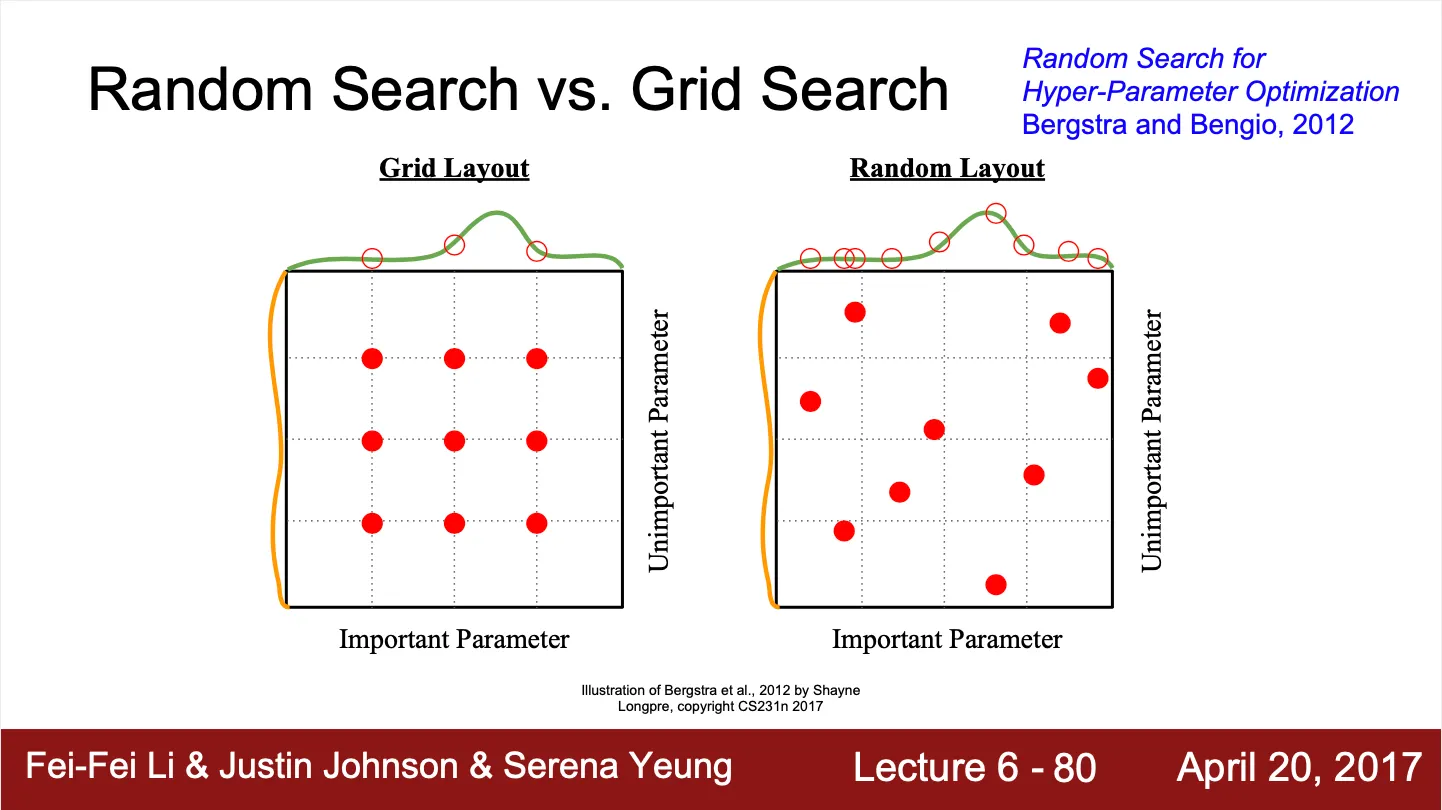
Random Search VS Grid Search

◦

Random Search 는 주어진 범위 안을 random 하게 실행해보는 것

◦

Grid Search 는 주어진 범위 안을 일정한 가격으로 실행해보는 것

◦

보통의 경우, Random Search 가 조금 더 일반성을 대변할 수 있음

•

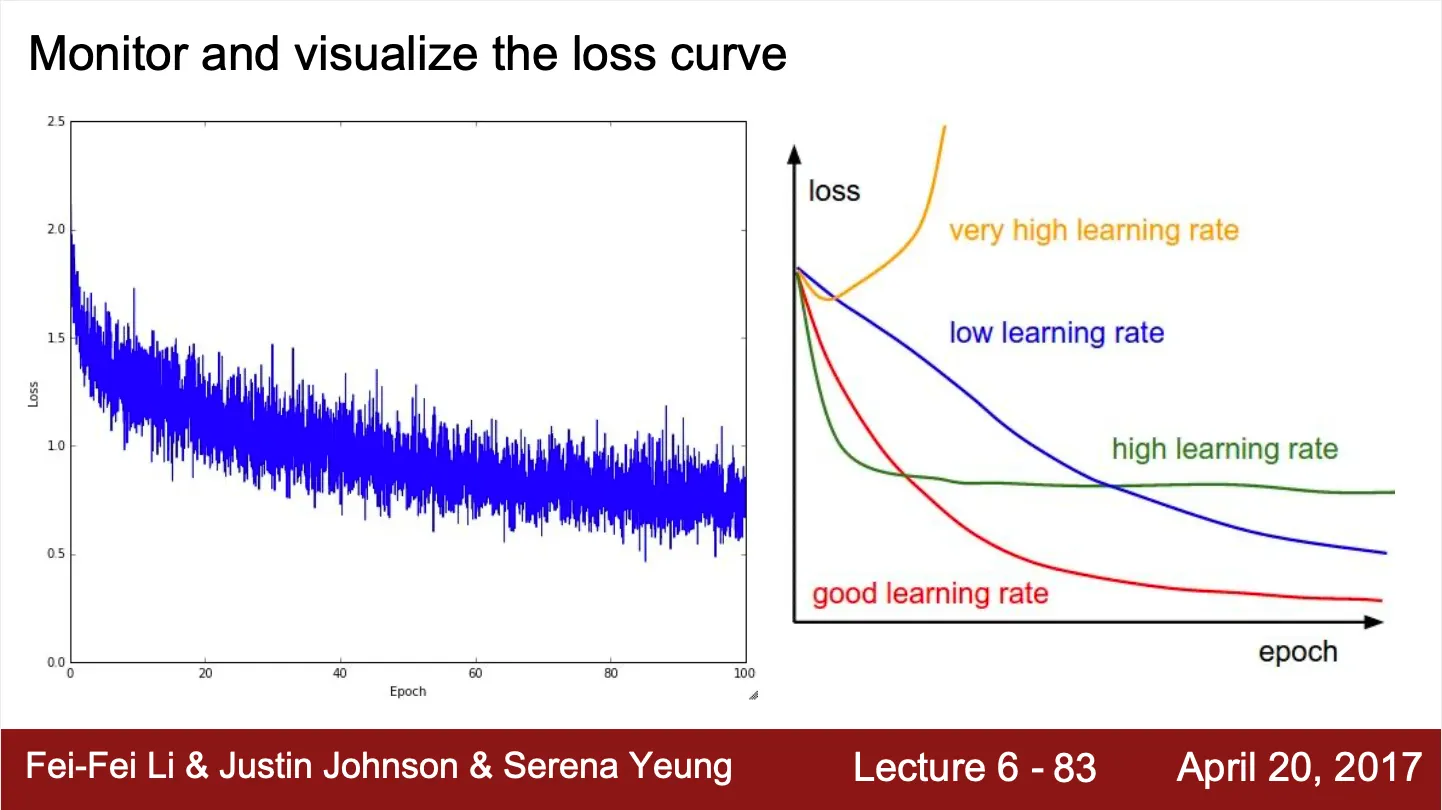
Loss Curve Monitoring

◦

Loss curve 를 모니터링 함으로서 학습이 잘 진행되는지 확인할 수 있음

◦

매우 큰 learning rate 는 loss explosion 을 야기

◦

큰 learning rate 는 빠른 loss 의 감소를 가져오지만, 수렴 지점이나 수렴성 측면에서 좋지 못함

◦

작은 learning rate 는 느린 loss 의 감소를 가져오지만, 수렴성 측면에서는 좋음

◦

좋은 learning rate 는 빠르면서도, 좋은 수렴성을 가지는 수치

◦

만약 처음 loss 가 처음 일정한 구간을 보이고 낮아지기 시작한다면, bad initialization 을 의심해 볼 수 있음

•

Training Accuracy VS Test Accuracy

◦

Gap 이 크다면 overfitting 을 의심해 볼 수 있음. 네트워크의 복잡도를 줄이거나, regularization 을 추가해보는 형태로 가야함

◦

Gap 이 작다면 오히려 네트워크의 복잡도를 늘려서 정확도를 높일 수 있는지 봐야함

•

Weight 와 Weight Update ratio ?

◦

보통 0.001 정도가 되는 것이 좋으나, 상황에 따라 다름

◦

꾸준히 모니터링하여 weight 에 비해 너무 큰, 혹은 너무 변화가 일어나는지를 보면 좋음 → Optimization technique 로 극복할 수 있어보임