Duplicate

Lecture 4 | Introduction to Neural Network

포스팅 날짜
2021/08/10
지난 강의 보기 - Lecture 3 | Loss Functions and Optimization

Note Taking

Lecture 3 요약
•
Loss
◦
prediction/score (s=f(x;W)=Wxs=f(x;W)=Wx) 이 얼마나 나쁜지를 평가하는 척도
◦
SVM Loss
◦
Regularization - 복잡한 Model 에 대한 정규화 (penalize specific/general weight scale)
•
Optimization
◦
Loss 를 최소화하는 적합한 WW 찾기
◦
Gradient Descent
▪
Numerical Gradient - Slow, Approximat, Easy to Write
▪
Analytic Gradient - Fast, Exact, Error-Prone
Analytic Gradient 를 구하는 방법: Computational Graph
•
Computational Function 을 graph 로 표현
•
각 node 를 computation 으로 정의
•
Back Propagation 을 사용할 수 있다는 장점이 있음
◦
재귀적으로 chain rule 을 사용하여 각 변수에 대한 gradient 를 계산
◦
특히 CNN (AlexNet), Neural Turing Machine 등의 복잡한 계산 시 이점을 가짐
Back Propagation
•
각 요소(weight) 에 대한 gradient 계산
◦
Computational Function (모델이 나타내는 computation) ff
◦
f(x,y,z)=(x+y)zf(x,y,z)=(x+y)z
◦
computation +,×+,\times 를 기준으로 computation graph 를 그림
◦
q=x+yq=x+y, 이에 따라 ∂q∂x=1,∂q∂y=1\frac{\partial q}{\partial x}=1, \frac{\partial q}{\partial y}=1
◦
f=qzf=qz, 이에 따라 ∂f∂q=z,∂f∂z=q\frac{\partial f}{\partial q}=z, \frac{\partial f}{\partial z}=q
◦
위 두 식을 이용해서 x,yx, y 에 대한 최종 computation ff 의 편미분은 chain rule 로 구해낼 수 있음
◦
∂f∂x=∂f∂q∂q∂x\frac{\partial f}{\partial x}=\frac{\partial f}{\partial q}\frac{\partial q}{\partial x}, ∂f∂y=∂f∂q∂q∂y\frac{\partial f}{\partial y}=\frac{\partial f}{\partial q}\frac{\partial q}{\partial y}
◦
이 편미분 값은 computation ff 를 최소화하기 위한 각 요소의 변화 방향을 제시해줌
•
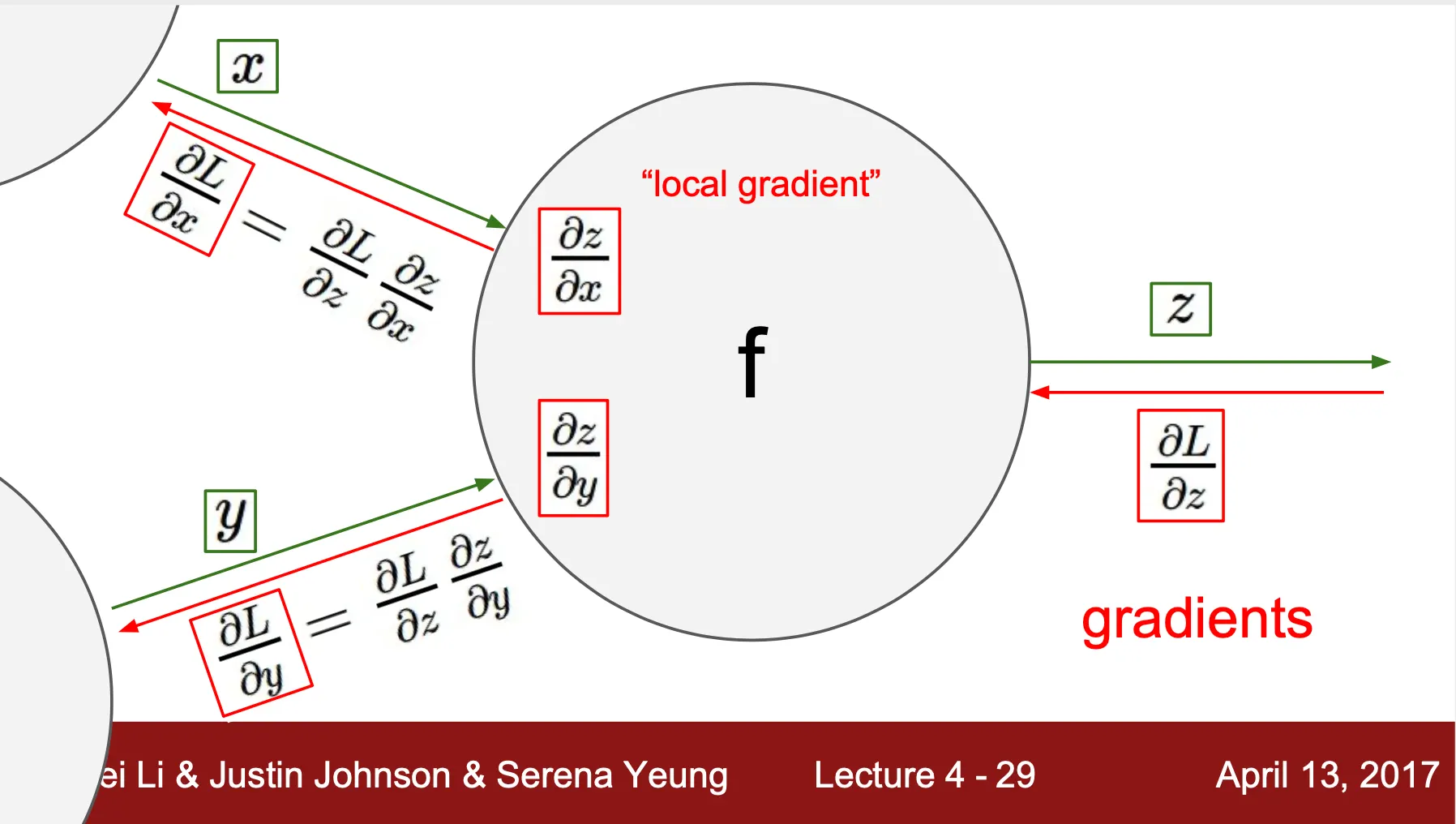
Computation Node 관점에서의 Back Propagation
◦
Upstream gradient + local gradient + chain rule 를 사용해 downstream gradient 를 계산
◦
Upstream gradient: ∂L∂z\frac{\partial L}{\partial z}
◦
Local gradient: ∂z∂x\frac{\partial z}{\partial x}, ∂z∂y\frac{\partial z}{\partial y}
◦
Chain rule: ∂L∂x=∂L∂z∂z∂x\frac{\partial L}{\partial x}=\frac{\partial L}{\partial z}\frac{\partial z}{\partial x}, ∂L∂z=∂L∂z∂z∂y\frac{\partial L}{\partial z}=\frac{\partial L}{\partial z}\frac{\partial z}{\partial y} 을 통해 downstream gradient 계산
◦
재귀적으로 Back Propagation 을 진행할 수 있음을 시사
•
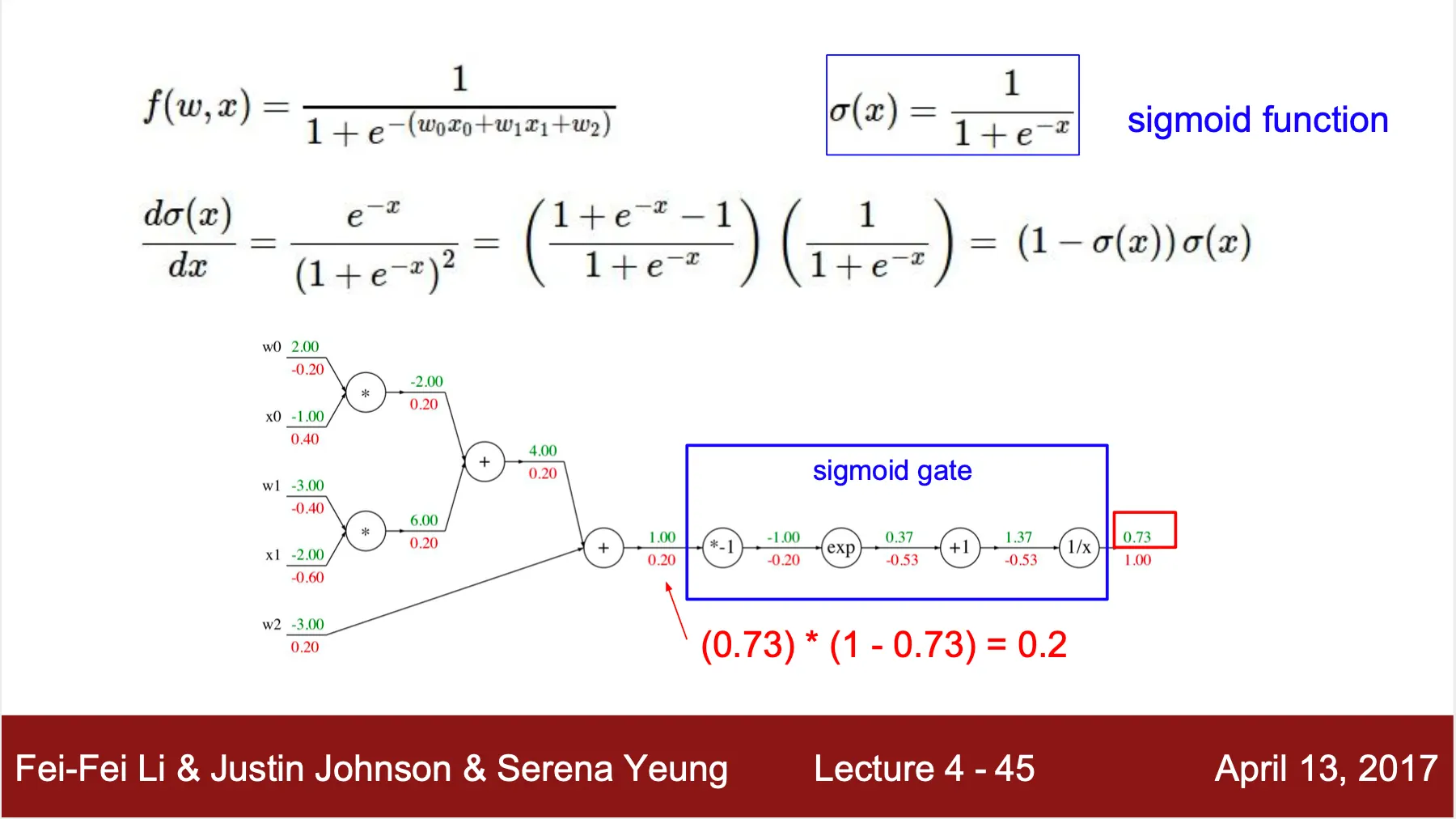
Complex Function 에서의 Back Propagation
◦
f(w,x)=11+e−(w0x0+w1x1+w2)f(w,x) = \frac{1}{1+e^{-(w_0x_0+w_1x_1+w_2)}}
◦
여러 computation 을 하나로 묶어 gate 로 정의할 수 있으며, 이 때의 back propagation 도 동일하게 진행할 수 있음 (sigmoid σ(x)=11+e−x\sigma(x)=\frac{1}{1+e^{-x}})
•
Patterns in backward flow - 각 computation node 의 표현?
◦
+ gate+ \rm\ {gate}: gradient distributor
▪
Local gradient 가 1 이기 때문에 upstream gradient 를 그대로 가져옴
◦
max⁡ gate\max\ \rm{gate}: gradient router
▪
Non-max 쪽은 관계가 끊기는 것과 같아 0
▪
Max 쪽은 local gradient 가 1 이기 때문에 upstream gradient 를 그대로 가져옴
◦
× gate\times\ \rm{gate}: gradient switcher
▪
Local gradient 가 피연산 변수 값이므로 upstream gradient ×\times 피연산자 값 으로 계산됨
•
Vectorized variable 에서의 Back Propagation
◦
기본적인 연산은 기존의 Back Propagation 과 동일하나, gradient 가 Jacobian Matrix 로 표현 (reference vector 의 ii 번째 항목이 loss vector 의 jj 번째 항목에 미치는 영향에 대한 결과)
◦
f(x,W)=∣∣W⋅x∣∣2=∑i=1n(W⋅x)i2f(x,W)=\left||W\cdot x |\right|^2=\sum_{i=1}^n(W\cdot x)_i^2
◦
q=W⋅x=[W1,1x1+⋯+W1,nxn⋯Wn,1x1+⋯+Wn,nxn]q=W\cdot x =\begin{bmatrix} W_{1,1}x_1+\cdots+W_{1,n}x_n \\ \cdots\\ W_{n,1}x_1+\cdots+W_{n,n}x_n \end{bmatrix}
▪
∂qk∂Wi,j={xjif i=k0else\frac{\partial q_k}{\partial W_{i,j}}= \begin{cases} x_j& \rm{if}\ \it{i=k} \\ 0& \rm{else} \\ \end{cases}
▪
∂qk∂xi=Wk,i\frac{\partial q_k}{\partial x_i}= W_{k,i}
◦
f=∣∣q∣∣2=q12+...qn2f=\left||q|\right|^2=q_1^2+...q_n^2
▪
∂f∂qk=2qk\frac{\partial f}{\partial q_k}=2q_k
◦
Upstream gradient: ∂L∂f=1\frac{\partial L}{\partial f}=1 로 설정 (L=fL=f)
◦
Chain rule step 1: ∂L∂q=∂L∂f∂f∂q\frac{\partial L}{\partial q}=\frac{\partial L}{\partial f}\frac{\partial f}{\partial q}
◦
Chain rule step 2: ∂L∂W=∑k∂f∂qk∂qk∂W\frac{\partial L}{\partial W}=\sum_k\frac{\partial f}{\partial q_k}\frac{\partial q_k}{\partial W}, ∂L∂x=∑k∂L∂qk∂qk∂x\frac{\partial L}{\partial x}=\sum_k\frac{\partial L}{\partial q_k}\frac{\partial q_k}{\partial x}
◦
∂L∂Wi,j=∂f∂Wi,j=∑k∂f∂qk∂qk∂Wi,j=2qixj\frac{\partial L}{\partial W_{i,j}}=\frac{\partial f}{\partial W_{i,j}}=\sum_k\frac{\partial f}{\partial q_k}\frac{\partial q_k}{\partial W_{i,j}}=2q_ix_j
◦
∂L∂xi=∂f∂xi=∑k∂f∂qk∂qk∂xi=∑k2qkWk,i=2WT⋅q\frac{\partial L}{\partial x_i}=\frac{\partial f}{\partial x_i}=\sum_k\frac{\partial f}{\partial q_k}\frac{\partial q_k}{\partial x_i}=\sum_k2q_kW_{k,i}=2W^T\cdot q
•
Modularized Implementation
◦
Forward - computation 진행, input 을 class variable 로 저장
◦
Backward = 저장한 class variable 과 upstream gradient 로 downstream gradient 반환
Neural Network
•
Neural Network 의 구성?
◦
기존에 다룬 linear score function 이 stack 된 형태
◦
Linear score function 사이의 non-linearity 존재
◦
최종적으로 non-linear complexed function 을 표현
•
Architecture
◦
기본적인 구조는 각 layer 의 연산이 matrix multiply (Fully-Connected)
◦
Input, Output Layer 사이의 layer 들은 hidden layer
◦
전체 layer 수에서 input layer 는 세지 않음 (총 4개의 layer 존재 시 3-layer Neural Network)
◦
Hidden layer 의 수로 명시하기도 함 (2-hidden-layer Neural Network)
Activation Function
•
자세히는 다음 시간에 언급
•
Sigmoid
•
tanh
•
ReLU
•
Leaky ReLU
•
Maxout
•
ELU
Feed-Forward Computation
•
입력을 정방향으로만 이동시키는 연산 (feed-forward)
•
단일 layer 연산을 Matrix Multiplication 의 형태로 모듈화 하여 구현 가능
•
전체 연산의 경우 모듈을 반복하여 합성함수 연산 진행