Lecture 13 | Generative Models

포스팅 날짜

2021/12/05

이전 강의 보기 - Lecture 12 | Visualizing and Understanding

다음 강의 보기 - Lecture 14 | Reinforcement Learning

Note Taking

Lecture 12 요약

•

What's going on inside ConvNets?

◦

First Layer - Oriented Edges & Opposing Color

◦

Last Layer - Activation map 이 nice feature representation

◦

Intermediate Layer

▪

일반적으로는, 크게 의미를 찾기는 어렵지만, 다양한 시도들이 존재

▪

Maximally Activated Patches

•

특정 Layer 의 activation 을 maximize 하는 patch 를 찾아냄

▪

Occlusion Experiment

•

특정 patch 영역을 제외하여 통과시킨 이미지의 결과가 score 에 얼마나 영향을 주느냐를 기준으로 patch 의 중요도를 찾아냄

▪

Sailency Map

•

Score 의 Input pixel 에 대한 gradient 로, 각 픽셀의 score 에 대한 중요도를 찾아냄

•

Gradient Ascent

◦

Last Layer 의 score, 혹은 Intermediate Layer 의 activation 을 maximize 하는 input 의 형태를 학습을 통해서 갱신해나가는 방법론

◦

I∗=arg max⁡If(I)+R(I)I^*=\argmax_I f(I) + R(I)I∗=argmaxI​f(I)+R(I)

▪

R(I)R(I) R(I) 는 이미지가 natural 하게 보이기 위한 regularization term - 일반적으로 L2

•

Feature Inversion

◦

주어진 feature vector 로부터 input image 를 reconstruction 하는 방법론

◦

생성된 이미지의 feature vector 와 주어진 이미지의 feature vector 와의 차이를 최소화하는 형태로 학습이 진행

◦

x∗=arg min⁡X∼RH×W×Cl(ϕ(x),ϕ0)+λR(x)x^*=\argmin_{X\sim \mathbb{R}^{\rm{H\times W\times C}}} l(\phi(x), \phi_0) + \lambda R(x)x∗=argminX∼RH×W×C​l(ϕ(x),ϕ0​)+λR(x)

•

Texture Synthesis

◦

특정 이미지의 texture 를 나타내는 항목인 Gram Matrix 개념 도입

▪

Feature vector 의 spatial dimension 을 없애고, 2-dimension 으로 만든 형태

▪

C×W×HC\times W\times HC×W×H 의 feature vector 를 W×HW\times HW×H 개의 CCC dimensional vector 로 나눈 뒤 2 개씩 짝지어 outer product 를 하여 생성된 C×CC\times CC×C matrix 의 mean 형태

•

Neural Style Transfer

◦

Content Image 의 content 를 가지면서, Style Image 의 style 을 따르는 이미지 generator

◦

Content Image, Style Image 두 장을 input 으로 받아서 Content Loss, Style Loss 를 최소화하는 형태로 학습을 진행하면서 input noise vector 를 갱신

Unsupervised Learning

•

Supervised Learning

◦

(x,y)(x,y)(x,y) where xxx is data and yyy is label

◦

Classification, Object Detection, Semantic Segmentation, Image Captioning

◦

Learn a function to map x→yx \to yx→y

•

Unsupervised Learning

◦

Just data xxx

◦

Clustering, Dimensionality Reduction, Feature Learning, Density Estimation

◦

Learn some underlying hidden structure of the data (Holy Grail: VIsual World 를 이해)

Generative Models: Overview

•

Training data ∼pdata(x)\sim p_{\rm{data}}(x)∼pdata​(x) , Generated samples ∼pmodel(x)\sim p_{\rm{model}}(x)∼pmodel​(x)

•

pmodel(x)p_{\rm{model}}(x)pmodel​(x) 가 pdata(x)p_{\rm{data}}(x)pdata​(x) 와 닮아있도록 학습

•

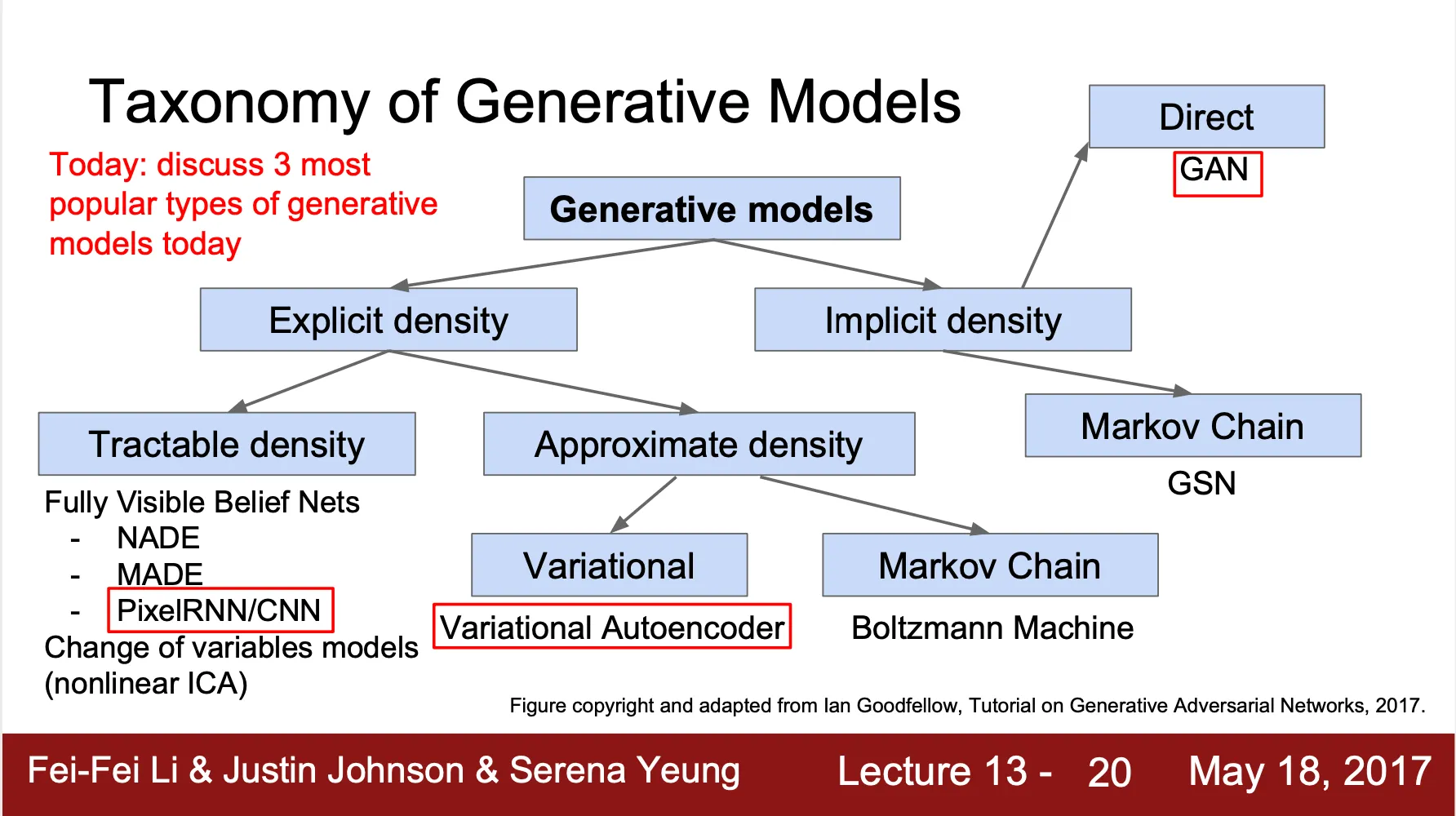
Taxonomy of Generative Models

◦

Explicit densitiy estimation

▪

Explicitly define and solve for pmodel(x)p_{\rm{model}}(x)pmodel​(x)

▪

ex) gaussan distribution 을 가정하고 진행

◦

Implicit density estimation

▪

Learn model that can sample from pmodel(x)p_{\rm{model}}(x)pmodel​(x)

PixelRNN & PixelCNN

•

Image X 의 likelihood

◦

p(X)=∏i=1np(xi∣x1,...,xi−1)p(X)=\prod_{i=1}^n p(x_i|x_1,...,x_{i-1})p(X)=∏i=1n​p(xi​∣x1​,...,xi−1​)

•

PixelRNN

◦

좌 상단부터 시작해서 근접한 pixel 의 값을 RNN (LSTM) 으로 찾아냄

◦

Sequential generation 이라 느림

•

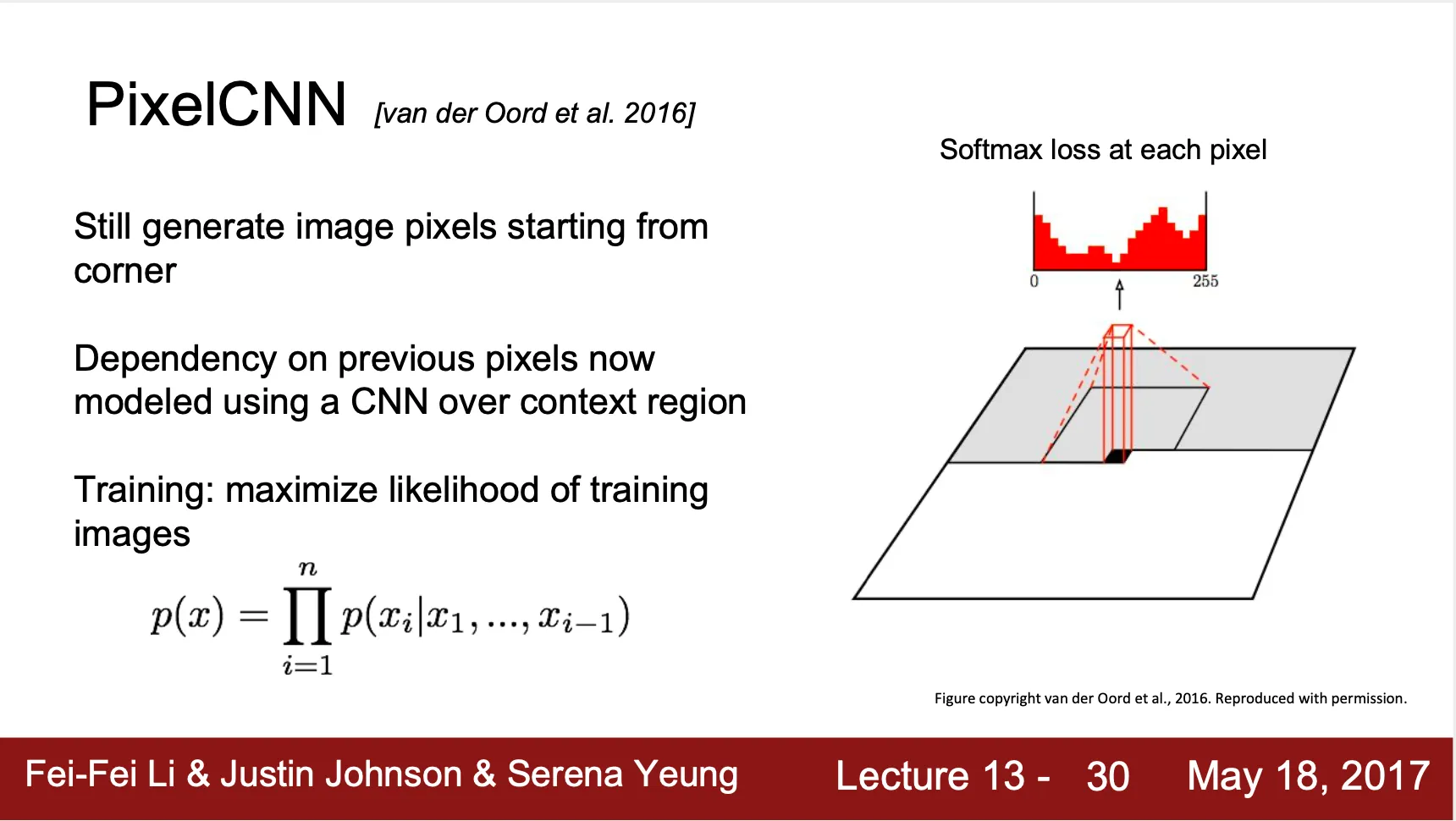
PixelCNN

◦

이전 영역들을 넣어 다음 pixel 값을 뽑아주는 CNN 으로 다음 pixel 을 찾아냄

◦

다음 pixel 의 값은 0~255 사이의 SoftMax ...

◦

Label 이 없고, 본인 데이터만으로 학습하기 때문에 unsupervised learning

•

장점

◦

직접적으로 likelihood p(x)p(x) p(x) 를 계산할 수 있음

◦

training data 로부터 계산된 likelihood p(x)p(x)p(x) 가 좋은 evaluation metric 이 됨

•

단점

◦

Generation 이 sequential 하기 때문에 느림

Variational Auto Encoder (VAE)

•

PixelCNN 은 tractable density function 을 사용했지만, VAE 는 latent vector zzz 에 대한 intractable density function 을 정의

◦

pθ(x)=∫pθ(z)pθ(x∣z)dzp_\theta(x)=\int p_\theta(z)p_\theta(x|z)dzpθ​(x)=∫pθ​(z)pθ​(x∣z)dz

•

Auto Encoder

◦

latent vector zzz : feature representation which dimension is smaller than input xxx

◦

zz z 를 학습하기 위해, zzz 로부터 reconstruction 하는 형태로 decoder 형태의 네트워크를 붙임 (좋은 representation 이라면, 재구성이 가능할 정보들을 담고 있어야 함-)

◦

L2 Loss 사용

◦

Training 한 이후, decoder 를 제거하고, extract 한 feature 를 사용해서 supervised model 로 사용함

•

Variational Auto Encoder

◦

Auto Encoder 의 변형으로, zzz 를 prior distribution pθ∗(z)p_{\theta^*}(z)pθ∗​(z) sample 한 뒤에 xxx 를 conditional distribution pθ∗(x∣z(i))p_{\theta^*}(x|z^{(i)})pθ∗​(x∣z(i)) 로부터 sampling

◦

pθ(x)=∫pθ(z)pθ(x∣z)dzp_\theta(x)=\int p_\theta(z)p_\theta(x|z)dzpθ​(x)=∫pθ​(z)pθ​(x∣z)dz

▪

pθ(z)p_\theta(z)pθ​(z) 는 prior distribution 으로 정의 가능

▪

pθ(x∣z)p_\theta(x|z)pθ​(x∣z) 는 네트워크의 output

▪

dzdzdz 를 기반한 적분이 계산 불가능!

▪

posterior density pθ(z∣x)=pθ(x∣z)pθ(z)/pθ(x)p_\theta(z|x) = p_\theta(x|z)p_\theta(z)/p_\theta(x)pθ​(z∣x)=pθ​(x∣z)pθ​(z)/pθ​(x) 도 분모 항 때문에 intractable

◦

posterior density 를 근사하여 구하는 방법론 사용

▪

pθ(z∣x)p_\theta(z|x)pθ​(z∣x) 를 근사하는 함수 qϕ(z∣x)q_\phi(z|x) qϕ​(z∣x) 를 정의하고 encoder 네트워크의 output 으로 설정

▪

encoder 는 gaussian distribution 의 mean, variance 를 학습

▪

mean, variance 를 통해 zzz 를 sampling 한 뒤, decoder 네트워크 통과

▪

decoder 네트워크를 통과한 결과가 output image (강의에서는 mean, variance 가 학습 결과로 나오는데 아닌듯!)

◦

Loss function 전개는 아래와 같고, 아래의 첫 두 항을 maximize 하는 것이 목표가 됨. (Maximum Likelihood Estimation)

\begin{align*} \log p_\theta(x^{(i)}) &= E_{z\sim q_\phi(z|x^{(i)})}[\log p_\theta(x^{(i)})] \\ &= E_z [\log \frac{p_\theta(x^{(i)}|z)p_\theta(z)}{p_\theta(z|x^{(i)})}] \\ &=E_z [\log \frac{p_\theta(x^{(i)}|z)p_\theta(z)}{p_\theta(z|x^{(i)})}\frac{q_\phi(z|x^{(i)})}{q_\phi(z|x^{(i)})}] \\ &= E_z[\log p_\theta(x^{(i)})|z]-E_z[\log\frac{q_\phi(z|x^{(i)})}{p_\theta(z)}] + E_z[\log\frac{q_\phi(z|x^{(i)})}{p_\theta(z|x^{(i)})}] \\ &= E_z[\log p_\theta(x^{(i)}|z)] - D_{KL}(q_\phi(z|x^{(i)})||p_\theta(z))+D_{KL}(q_\phi(z|x^{(i)})||p_\theta(z|x^{(i)})) \end{align*}

◦

이후, encoder 를 제거하고 normal distribution 에서 zzz 를 sampling 하여 decoder 를 통과시키면 generative model 로 사용 가능!

GAN

•

Explicit 하게 model density 를 계산하려는 생각에서 벗어나는 것은 어떨까-?

•

게임이론적 접근

◦

Generator Network: Discriminator 를 속이려 함

◦

Discriminator Network: 실제 이미지와 Generated 이미지를 정확히 구별하려 함

•

Minimax Loss Function

◦

min⁡θgmax⁡θd[Ex∼pdatalog⁡Dθd(x)+Ez∼pz(1−log⁡Dθd(Gθg(z)))]\min_{\theta_g}\max_{\theta_d}[\mathbb{E}_{\it{x\sim p_{data}}}\log D_{\theta_d}(x) + \mathbb{E}_{\it{z\sim p_{z}}}(1 -\log D_{\theta_d}(G_{\theta_g}(z)))]minθg​​maxθd​​[Ex∼pdata​​logDθd​​(x)+Ez∼pz​​(1−logDθd​​(Gθg​​(z)))]

◦

Discriminator 는 pdatap_{data}pdata​ 를 따르는 데이터 xxx 에 대해서 True (1) 로 판단하기를 원하고, pzp_zpz​ 를 따르는 데이터 zzz 에 대해 생성된 이미지 Gθg(z)G_{\theta_g}(z) Gθg​​(z) 는 False (0) 로 판단하기를 원함 → Maximize (Gradient Ascent)

◦

Generator 는  pzp_zpz​ 를 따르는 데이터 zzz 에 대해 생성된 이미지 Gθg(z)G_{\theta_g}(z) Gθg​​(z) 에 대해서 True (1) 로 판단하기를 원함 → Minimize (Gradient Descent)

◦

다만, (1−log⁡Dθd(Gθg(z)))(1 -\log D_{\theta_d}(G_{\theta_g}(z)))(1−logDθd​​(Gθg​​(z))) 는 Dθd(Gθg(z))D_{\theta_d}(G_{\theta_g}(z))Dθd​​(Gθg​​(z)) 가 0 에 가까울 때, 즉 generator 가 기능을 잘 못할 때 gradient 가 상당히 flat 하여 학습이 잘 되지 않는 문제가 있음

◦

때문에, Generator 의 경우 max⁡θgEz∼p(z)log⁡(Dθd(Gθg(z)))\max_{\theta_g}\mathbb{E}_{z \sim p(z)} \log(D_{\theta_d}(G_{\theta_g}(z)))maxθg​​Ez∼p(z)​log(Dθd​​(Gθg​​(z))) 에 대한 Gradient Ascent 로 문제를 바꾸어서 해결

◦

 Discriminator Train (weight update) → Generator Train (weight update) 반복

◦

 ICLR 2016, Alex Radford 가 Convolutional GAN 제시

•

두 개의 random noise z1,z2z_1,z_2z1​,z2​ 사이를 interpolate 하여 생성한 이미지도 smooth 하게 이어짐

•

Random Noise 간의 mathematics 가 성립 (for fun)

•

장점

◦

State-of-the-art (performance)

•

단점

◦

unstable to train

◦

Inference query p(x),p(z∣x)p(x), p(z|x)p(x),p(z∣x) 에 대해서 시사하는 바가 없음