Lecture 14 | Reinforcement Learning

포스팅 날짜

2021/12/07

이전 강의 보기 - Lecture 13 | Generative Models

다음 강의 보기 -

Note Taking

Lecture 13 요약

•

Unsupervised Learning

◦

학습 데이터는 있지만 그에 해당하는 label 이 존재하지 않는 학습

◦

ex) Clusterinf, Dimension Reduction

•

PixelRNN, PixelCNN

◦

Sequential 하게 다음 픽셀을 생성하는 네트워크를 학습

◦

학습 속도가 굉장히 느림

•

Variational Auto Encoder (VAE)

◦

Intractable density function pθ(x)=∫pθ(z)pθ(x∣z)dzp_\theta(x)=\int p_\theta(z)p_\theta(x|z)dzpθ​(x)=∫pθ​(z)pθ​(x∣z)dz

◦

density function 을 근사하기 위해 variational inference 도입

\begin{align*} \argmax_\theta p_\theta(x^{(i)})&=\argmax_\theta\log p_\theta(x^{(i)}) \\ &= \argmax_\theta \log [\int p_\theta(z)p_\theta(x^{(i)}|z)dz] \\ &= \argmax_\theta \log [\int p_\theta(x^{(i)})p_\theta(z|x^{(i)})dz] \\ &= \argmax_\theta \log p_\theta(x^{(i)})\int p_\theta(z|x^{(i)})dz \\ &= \argmax_\theta\mathbb{E}_{z \sim q_\phi(z|x^{(i)})} \log p_\theta(x^{(i)}) \\ &= \argmax_\theta\mathbb{E}_{z \sim q_\phi(z|x^{(i)})} [\log \frac{p_\theta(x^{(i)}|z)p_\theta(z)}{p_\theta(z|x^{(i)})}] \\ &=\argmax_\theta\mathbb{E}_{z \sim q_\phi(z|x^{(i)})} [\log \frac{p_\theta(x^{(i)}|z)p_\theta(z)}{p_\theta(z|x^{(i)})}\frac{q_\phi(z|x^{(i)})}{q_\phi(z|x^{(i)})}] \\ &= \argmax_\theta (\mathbb{E}_{z \sim q_\phi(z|x^{(i)})}[\log p_\theta(x^{(i)})|z]-\mathbb{E}_{z \sim q_\phi(z|x^{(i)})}[\log\frac{q_\phi(z|x^{(i)})}{p_\theta(z)}] + \mathbb{E}_{z \sim q_\phi(z|x^{(i)})}[\log\frac{q_\phi(z|x^{(i)})}{p_\theta(z|x^{(i)})}]) \\ &= \argmax_\theta (\mathbb{E}_{z \sim q_\phi(z|x^{(i)})}[\log p_\theta(x^{(i)}|z)] - D_{KL}(q_\phi(z|x^{(i)})||p_\theta(z))+D_{KL}(q_\phi(z|x^{(i)})||p_\theta(z|x^{(i)}))) \end{align*}

◦

encoder 를 붙여 qϕ(z∣x(i))q_\phi(z|x^{(i)})qϕ​(z∣x(i)) 를 학습 (mean, variance)

◦

encoder 를 통해 학습한 분포에서 reparametrization trick 을 사용해 sampling

◦

sampling 한 zzz 를 사용해 loss 계산 후 back propagation

•

Generative Adversarial Network (GAN)

◦

Generator: noise vector로 부터 학습 데이터의 분포와 유사한 이미지를 생성하여 discriminator 를 속이는 것이 목적

◦

Discriminator: Generator 가 생성한 이미지를 fake 로, 실제 이미지를 real 로 정확하게 판단하는 것이 목적

◦

Minimax Loss Function

\min_{\theta_g}\max_{\theta_d}[\mathbb{E}_{\it{x\sim p_{data}}}\log D_{\theta_d}(x) + \mathbb{E}_{\it{z\sim p_{z}}}(1 -\log D_{\theta_d}(G_{\theta_g}(z)))]

Reinforcement Learning

•

Reward 를 제공하는 environment, 그리고 그와 상호작용하는 agent 를 포함하는 문제에서 Reward 를 maximize 하는 목적을 가지는 학습

•

State sts_tst​ : Environment → Agent
Action ata_tat​ : Agent → Environment
Reward rtr_trt​ : Environment → Agent

Environment 가 ternminal state 에 도착하기 전까지 ttt 가 증가하며 루프 반복

•

Example 1. Cart-Pole Problem
Objective: 움직이는 카트에서 pole 을 수직으로 세우는 것

State: pole 의 각도, pole 의 각속도, 카트의 수평 속도 등
Action: 카트에 가하는 수평 힘
Reward: pole 이 수직인 time step 마다 1

•

Example 2. Robot Locomotion
Objective: 로봇이 수평으로 걷게 하는 것

State: 모든 관절의 각도와 위치
Action: 관절에 가해지는 토크
Reward: 로봇이 똑바로 서 있으면서 앞으로 걷는 time step 마다 1

•

Example 3. Atari Game
Objective: 최대한 높은 점수로 게임을 끝마치는 것

State: 게임 화면의 raw pixel 들
Action: 컨트롤러의 4 개 커맨드 컨트롤 중 하나
Reward: 각 time step 마다 1

Markov Decision Process

•

Reinforcement Learning 문제를 수학적으로 형성하는 방법

•

Markov Property

◦

현재의 state 가 다음 state 를 전적으로 결정하는 성질

•

5 가지의 요소로 정의

◦

(S,A,R,P,γ)(S,A,R,\mathbb{P}, \gamma)(S,A,R,P,γ)

◦

 SSS: 가능한 state 들의 종류

◦

AAA: 가능한 action 들의 종류

◦

RRR: (state, action) pair 마다의 reward 

◦

P\mathbb{P}P: (state, action) pair 마다의 다음 state 로의 전이 확률

◦

γ\gammaγ: state 변화 시  reward 에 곱해지는 값

•

다음 순서로 process 가 진행

t=0t=0t=0 일 때, initial sate 를 sampling s0∼p(s0)s_0 \sim p(s_0)s0​∼p(s0​)

끝날 때 (Terminal State)까지 다음을 반복

Agent 가 action ata_tat​ 를 선택

Environment 가 reward 를 sampling rt∼R(.∣st,at)r_t \sim R(. | s_t, a_t)rt​∼R(.∣st​,at​)

Environment 가 다음 state 를 sampling st+1∼P(.∣st,at)s_{t+1} \sim P(.|s_t, a_t)st+1​∼P(.∣st​,at​)

Agent 가 reward rtr_trt​ 를 받고 다음 state st+1s_{t+1}st+1​ 로 진입

•

Policy π\piπ 는 state → action 인 함수

•

목적은 ∑t>0γtrt\sum_{t>0} \gamma^t r_t∑t>0​γtrt​ 를 최대화하는 π∗\pi^*π∗ 를 찾는 것

•

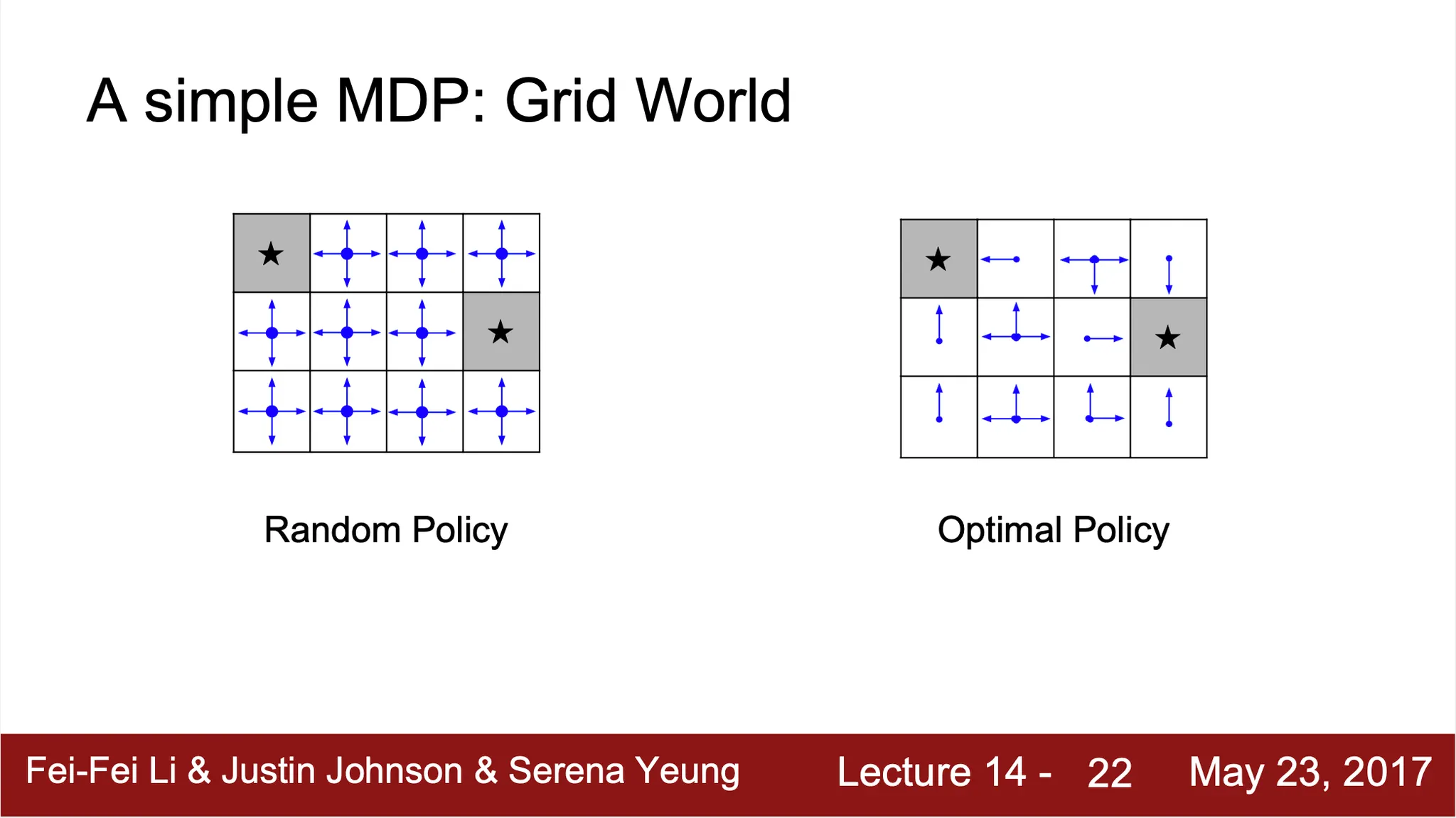
Example. Grid World 

•

π∗\pi^*π∗ 를 찾는 방법 → expected sum of rewards 를 maximize 
π∗=arg max⁡πE[∑t≥0γtrt∣π]\pi^* = \argmax_\pi \mathbb{E}[\sum_{t\ge0}\gamma^t r^t | \pi]π∗=argmaxπ​E[∑t≥0​γtrt∣π]

•

How good is a state: Value Function

◦

Vπ(s)=E[∑t≥0γtrt∣s0=s,π]V^\pi(s) = \mathbb{E} [\sum_{t\ge0} \gamma^t r_t|s_0=s,\pi]Vπ(s)=E[∑t≥0​γtrt​∣s0​=s,π]

•

How good is a state-action pair: Q-value Function

◦

Qπ(s,a)=E[∑t≥0γtrt∣s0=s,a0=a,π]Q^\pi(s,a)=\mathbb{E}[\sum_{t\ge0} \gamma^t r_t|s_0=s, a_0=a, \pi]Qπ(s,a)=E[∑t≥0​γtrt​∣s0​=s,a0​=a,π]

◦

Optimal 한 Q∗(s,a)=max⁡πE[∑t≥0γtrt∣s0=s,a0=a,π]Q^*(s,a)=\max_\pi\mathbb{E}[\sum_{t\ge0} \gamma^tr_t|s_0=s,a_0=a,\pi]Q∗(s,a)=maxπ​E[∑t≥0​γtrt​∣s0​=s,a0​=a,π]

◦

이 때, Q∗Q^*Q∗ 은 Bellman Equation 을 만족

▪

Q∗(s,a)=Es′∼ϵ[r+γmax⁡a′Q∗(s′,a′)∣s,a]Q^*(s,a) =\mathbb{E}_{s'\sim\epsilon}[r+\gamma\max_{a'}Q^*(s',a')|s,a]Q∗(s,a)=Es′∼ϵ​[r+γmaxa′​Q∗(s′,a′)∣s,a]

▪

다음 스텝 이후의 Q-value Function 의 최댓값이 Q∗(s′,a′)Q^*(s',a')Q∗(s′,a′) 로 주어진다면, 현재 스텝에서는 r+γQ∗(s′,a′)r+\gamma Q^*(s',a')r+γQ∗(s′,a′) 의 기댓값을 최대로 만드는 action 을 취하는 직관에서 시작

◦

Bellman Equation 을 풀어 Q∗Q^*Q∗ 를 얻어내자!

▪

가장 기본적인 방법: Value Iteration algorithm

▪

Qi+1(s,a)=E[r+γmax⁡a′Qi(s′,a′)∣s,a]Q_{i+1}(s,a) = \mathbb{E}[r+\gamma\max_{a'}Q_i(s',a')|s,a]Qi+1​(s,a)=E[r+γmaxa′​Qi​(s′,a′)∣s,a]

▪

QiQ_iQi​ 가 i→∞i\to \infini→∞ 일 때 Q∗Q^*Q∗ 

▪

하지만, state 가 굉장히 많은 경우에 현실적으로 불가능... → Neural Network 로 찾자!

Q-Learning

•

Q-Value Function 을 예측하기 위한 function approximator 를 사용하는 방법

•

Function approximator 로 deep neural network 를 사용하면 Deep Q-Learning

•

 Loss function

◦

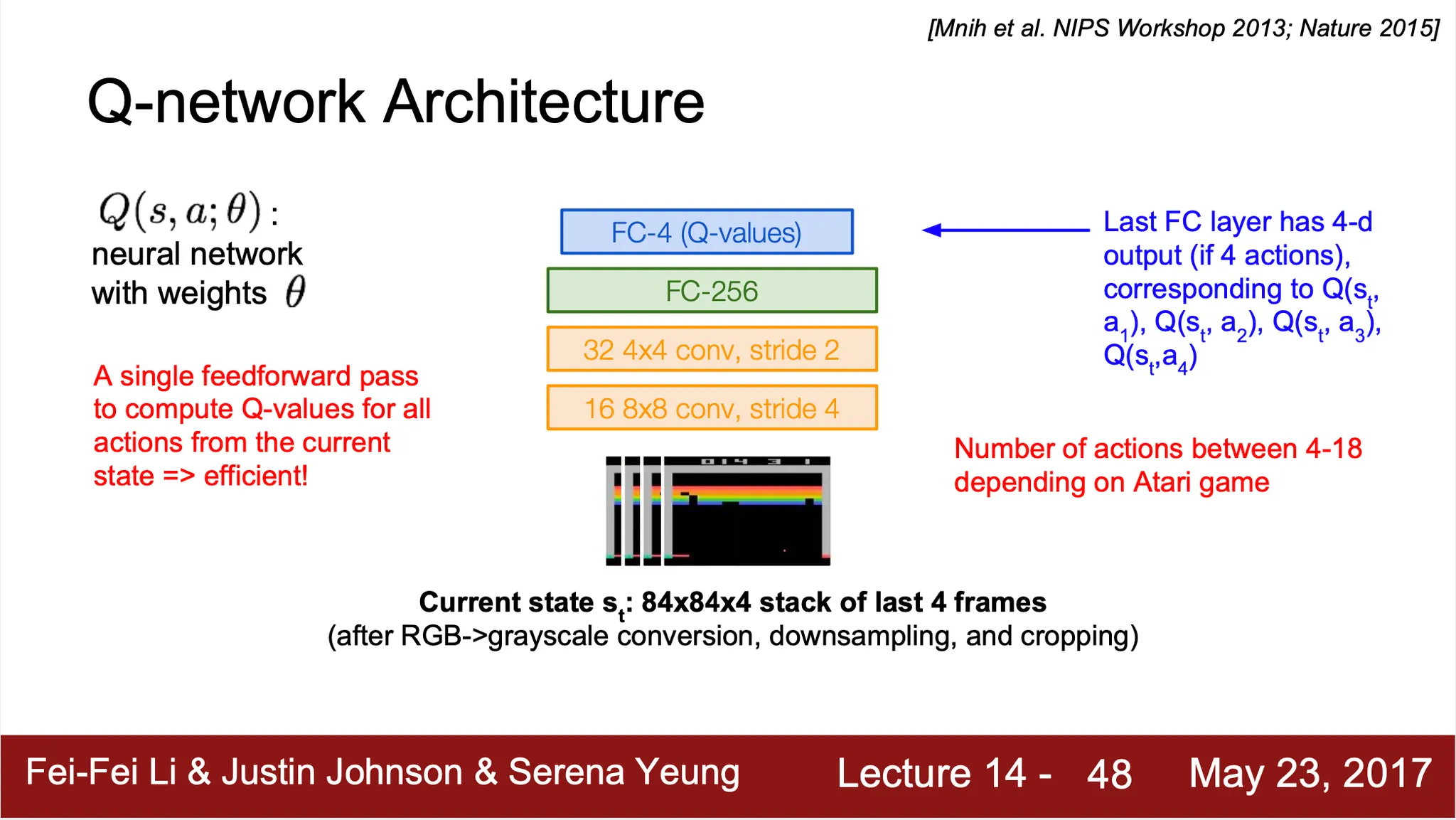
Li(θi)=Es,a∼σ(⋅)[(yi−Q(s,a;θi))2]L_i(\theta_i)=\mathbb{E}_{s,a\sim\sigma(\cdot)}[(y_i-Q(s,a;\theta_i))^2]Li​(θi​)=Es,a∼σ(⋅)​[(yi​−Q(s,a;θi​))2]

•

Example. Atari Game

◦

Input: 현재 상태

◦

Output: 각 action 을 선택했을 때 해당하는 Q-value

◦

단일 forward pass 만으로 현재 상태에서 모든 action 에 대한 Q-value 를 구해낼 수 있음!

Training the Q-Network: Experience Replay

•

기존 Q-Network 학습의 문제점

◦

현재 상태의 Q-Network 가 다음 training sample 을 결정하는 형태의 학습

▪

input sample 들이 서로 관계가 있어 학습 효율이 떨어짐

▪

잘못된 피드백 루프에 빠질 수 있음

•

 Experience Replay

◦

각 time step 별로 얻은 다음 sample 을 tuple 형태로 data set 에 저장해두고, 해당 data set 에서 random 하게 뽑아서 mini batch 를 구성하고, 학습 데이터로 사용

Policy Gradients

•

로봇이 물체를 집는 행위는 관절 위치, 속도 등 다양한 상태가 존재하는 문제에 대해서 Q-Learning 은 매우 복잡함

•

대략적으로 optimal policy 를 알고 있을 때, policy 들 중에서 가장 좋은 policy 를 얻어낼 수 없을까-

•

State 에 따른 Action (Policy) 를 직접 output 으로 내는 네트워크의 학습 

•

Policy 에 대한 평가 - Value of policy

\theta^*=\argmax_\theta J(\theta)

를 만족하는

\theta

를 찾자!

J(\theta)=\mathbb{E}[\sum_{t\ge0}\gamma^t t_t | \pi_\theta]

•

REINFORCE algorithm

◦

Policy 로 부터 sampling 한 trajenctory τ\tauτ 에 대해,

\begin{align*} J(\theta)&=\mathbb{E}_{\tau\sim p(\tau;\theta)}[r(\tau)]\\ &=\int_\tau r(\tau)p(\tau;\theta)d\tau \end{align*}

◦

해당 Value of Policy 의 미분 값? (for gradient ascent)
Expectiation 의 gradient 를 gradient 의 expectation 으로 치환할 수 있음!

\begin{align*} \nabla_\theta J(\theta)&=\int_\tau r(\tau) \nabla_\theta p(\tau;\theta)d\tau \\ &=\int_\tau r(\tau) p(\tau;\theta)\frac{\nabla_\theta p(\tau;\theta)}{p(\tau;\theta)}d\tau \\ &=\int_\tau r(\tau) p(\tau;\theta)\nabla_\theta\log p(\tau;\theta)d\tau \\ &= \mathbb{E}_{\tau\sim p(\tau;\theta)}[r(\tau)\nabla_\theta\log p(\tau;\theta)] \end{align*}

◦

Transition probabilites 는 Value of Policy 의 gradient 를 계산하는 데 불필요!

\begin{align*} &p(\tau;\theta) =\prod_{t\ge0}p(s_{t+1}|s_t,a_t)\pi_\theta(a_t|s_t) \\ &\log p(\tau;\theta) = \sum_{t\ge0}\log p(s_{t+1}|s_t,a_t)+\log \pi_\theta (a_t|s_t) \\ &\nabla_\theta\log p(\tau;\theta)=\sum_{t\ge0}\nabla_\theta\log\pi_\theta(a_t|s_t) \end{align*}

◦

위 식 전개 덕분에, 하나의 sampling 된 trajectory τ\tauτ 에 대한 gradient 는 다음과 같이 구해냄 (expectation 말고 expectation 내부에 있는 term 만!)

\nabla_\theta J(\theta) \approx\sum_{t\ge0}r(\tau)\nabla_\theta\log\pi_\theta(a_t|s_t)

◦

위 항목을 Gradient Estimator 라 칭함 (하나의 input trajectory 에 대한 gradient)

◦

이 때, r(τ)r(\tau)r(τ) 가 높다면, τ\tauτ 속에서 관찰된 state 속에서의 action 의 확률을 높이고 낮다면 확률을 낮추는 직관을 사용 (ex. Atari Game 에서 고득점 받은 플레이어의 상황에 따른 이동들[trajectory] 에 reward 가 부여되었을 것이므로 해당 상황 속 이동들이 나올 확률을 높이는 것)

◦

하지만, 위 직관은 또 high variance problem 을 야기함. 굉장히 많은 sample 이 존재해야 진짜 정답에 가까워지고, 적당히 많아서는 그냥 지금까지 많았던 데이터의 경향성 쪽으로 해당 state 에서의 해당 action 의 좋고 나쁨을 판단해버릴 수 있음.

◦

때문에 variation reduction 에 대한 시도를 진행함!

Trajectory 내 어떤 state, action 에 대한 push up probability 정도를 결정하기 위한 reward 부분을 trajectory 전체의 reward 가 아닌, 해당 state 이후의 reward 만으로 계산. 이는 해당 state 에서의 action 이 얼마나 좋고 나쁜지 판단할 때, future reward 만을 계산해야 한다는 직관에서 유래함.

\nabla_\theta J(\theta) \approx\sum_{t\ge0}(\sum_{t'\ge t}r_{t'})\nabla_\theta\log\pi_\theta(a_t|s_t)

1 번의 방법에 reward 에 대한 discount factor 를 추가하여 계산. 현재 상태를 기준으로 future reward 만 계산하되 아주 먼 미래의 reward 는 현재 state action 이 영향을 주었다고 보기 힘들기 때문에 점점 감소되는 reward 를 주는 직관에서 유래 (실제로 a → b → c 경로 뿐 아니라 a → d → c 등 같은 결과가 나오더라도 b, d 등 중간단계는 다를 수 있기 때문)

\nabla_\theta J(\theta) \approx\sum_{t\ge0}(\sum_{t'\ge t}\gamma^{t'-t} r_{t'})\nabla_\theta\log\pi_\theta(a_t|s_t)

Reward 가 높냐 낮냐 얼마냐가 중요한 것이 아니라, reward 가 생각한 것보다 높냐, 낮냐가 중요. 생각한 것보다- 의 기준이 baseline.

\nabla_\theta J(\theta) \approx\sum_{t\ge0}(\sum_{t'\ge t}\gamma^{t'-t} r_{t'}-b(s_t))\nabla_\theta\log\pi_\theta(a_t|s_t)

◦

3 번의 baseline 으로 사용하는 것이 Q-Value Function 과 Value Function 의 차이 (State 에서 선택할 수 있는 수 많은 선택지들에 비해서 해당 선택지가 얼마나 더 좋냐!)

\nabla_\theta J(\theta) \approx\sum_{t\ge0}(Q^{\pi_\theta}(s_t,a_t)-V^{\pi_\theta}(s_t))\nabla_\theta\log\pi_\theta(a_t|s_t)

◦

하지만, 위의 Q, V 는 Policy Gradient 를 위한 REINFORCE algorithm 에서 구해낼 수 없었음. 이를 위해 새로운 Actor-Critic Algorithm 을 도입

•

Actor-Critic Algorithm

◦

Policy Gradient 에 Q-Learning 을 섞어 actor (the Policy) 와 critic (Q-Value Function) 를 동시에 학습하는 방법론 

•

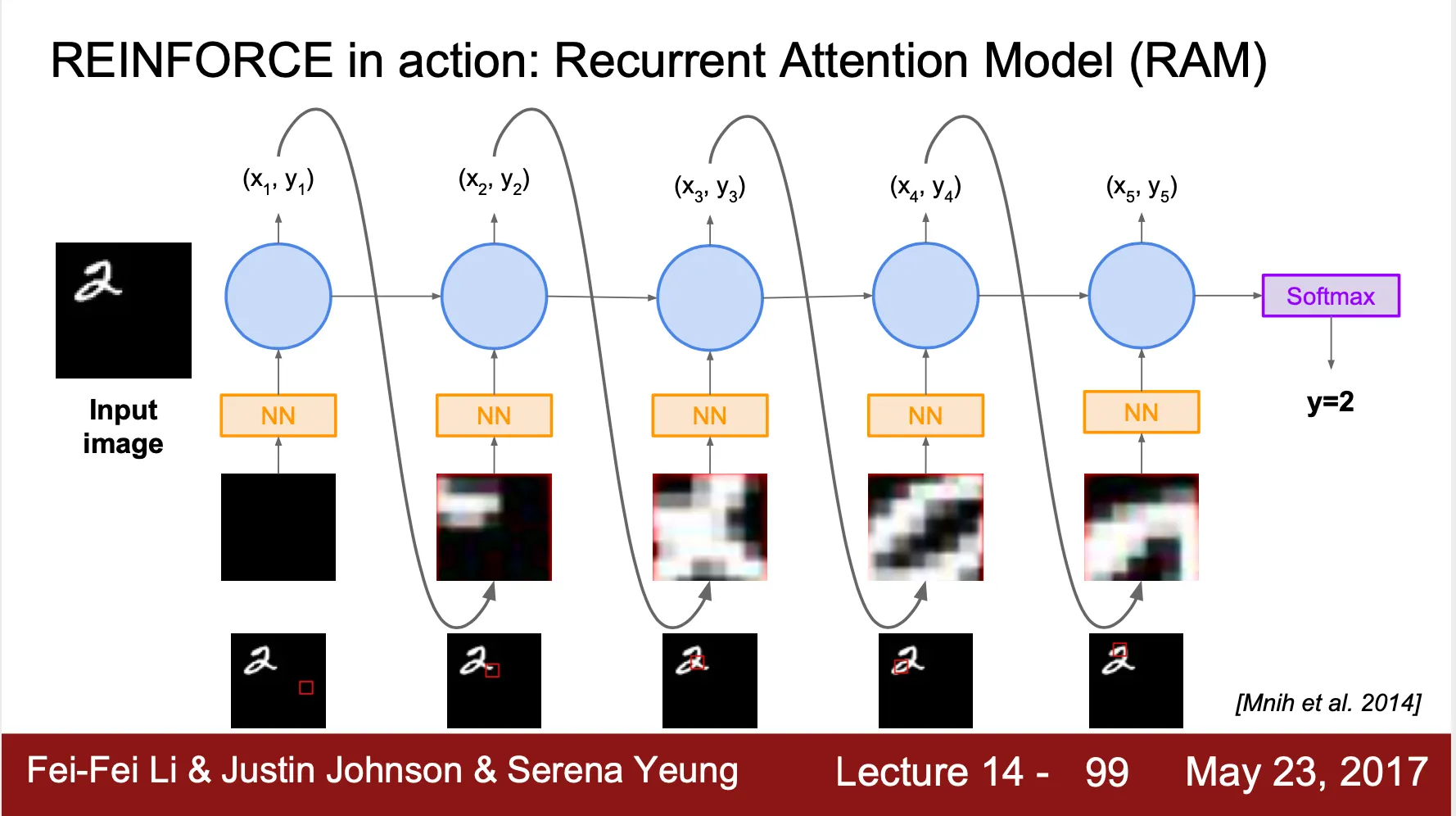
REINFORCE in action: Recurrent Attention Model (RAM)

◦

State: 현재까지 관찰한 glimpses 들의 모음

◦

Action: 다음 볼 glimpse 의 coordinate

◦

Reward: final timestamp 에서 image 가 정확하게 classified 되었으면 1, 아니면 0