본 포스트에서는 기존에 2D 이미지 생성에서 많이 사용되었던 Diffusion Model 을 사용하여 Implicit Neural Field 의 생성을 처음으로 타겟팅한 논문에 대해서 소개드리려고 합니다.
Project Page 및 논문을 직접 읽어보시고 싶으신 분들은 위 링크를 참고하시면 좋습니다.
Objective
3D 분야에서 Implicit Neural Fields 는 coordinates 를 입력으로 받아 volume density, signed distance 와 같이 occupancy 나 underlying surface 를 나타낼 수 있는 요소들을 출력으로 내는 MLP 를 나타냅니다. 이러한 표현 방식은 기존의 Voxel Grid, Mesh, Point Cloud 등에 비해서 높은 fidelity 를 보여주었고, 연구에 적극적으로 활용되기 시작했습니다.
NeRF: Example of Implicit Neural Fields
위의 영상은 Implicit Neural Fields 의 한 예시인 NeRF 로, Novel View 에서의 렌더링 이미지를 예측할 수 있는 task 입니다. NeRF 에서는 coordinates 를 입력으로 받아 volume density 와 color 를 산출하고, 이를 기반으로 Novel View 에서의 Volume Rendering 을 통해 이미지를 생성해낼 수 있습니다.
이러한 Implicit Neural Fields 는 grid, vertex, face 와 같이 geometry 를 결정하는 직접적인 데이터를 가지고 있는 explicit representations 와는 달리 데이터 자체가 geometry 에 대한 설명이 추상적인 것이 특징입니다. 더불어 background 를 포함한 scene 까지 표현할 수 있는 능력 때문에, 하나의 scene 에 대해 optimized 된 Implicit Neural Fields 를 하나의 데이터로 하여 이러한 Implicit Neural Fields 라는 데이터를 생성하는 접근이 굉장히 어렵고 많이 없었습니다.
HyperDiffusion: (Left) Generated 3D Shape, (Right) Generated 4D Animation
논문에서는 Implicit Neural Fields (의 weights) 를 하나의 데이터로 하여 새로운 Implicit Neural Fields 를 생성하는 시도를 합니다. 이를 위해 기존의 DIffusion Model 을 사용하며, 이미지 단에서 Diffusion Model 을 사용했던 기존의 틀에서 벗어나 Implicit Neural Fields (MLP) parameters 를 생성하는 모델로 이를 활용합니다. 특이한 점은, 3D 뿐만 아니라 시간까지 포함한 4D 의 경우에서도 성공적인 결과를 보여줍니다.
Method
논문에서 제시한 HyperDiffusion 은 MLP 네트워크로 구성된 Implicit Neural Fields 를 생성하는 unconditional generative model 입니다. 논문에서는 MLP parameters 를 생성하는 파이프라인을 구축하고, 이 파이프라인을 통해서 생성된 MLP parameters 로 새로운 Implicit Neural Fields 를 만들어내는 개념입니다.
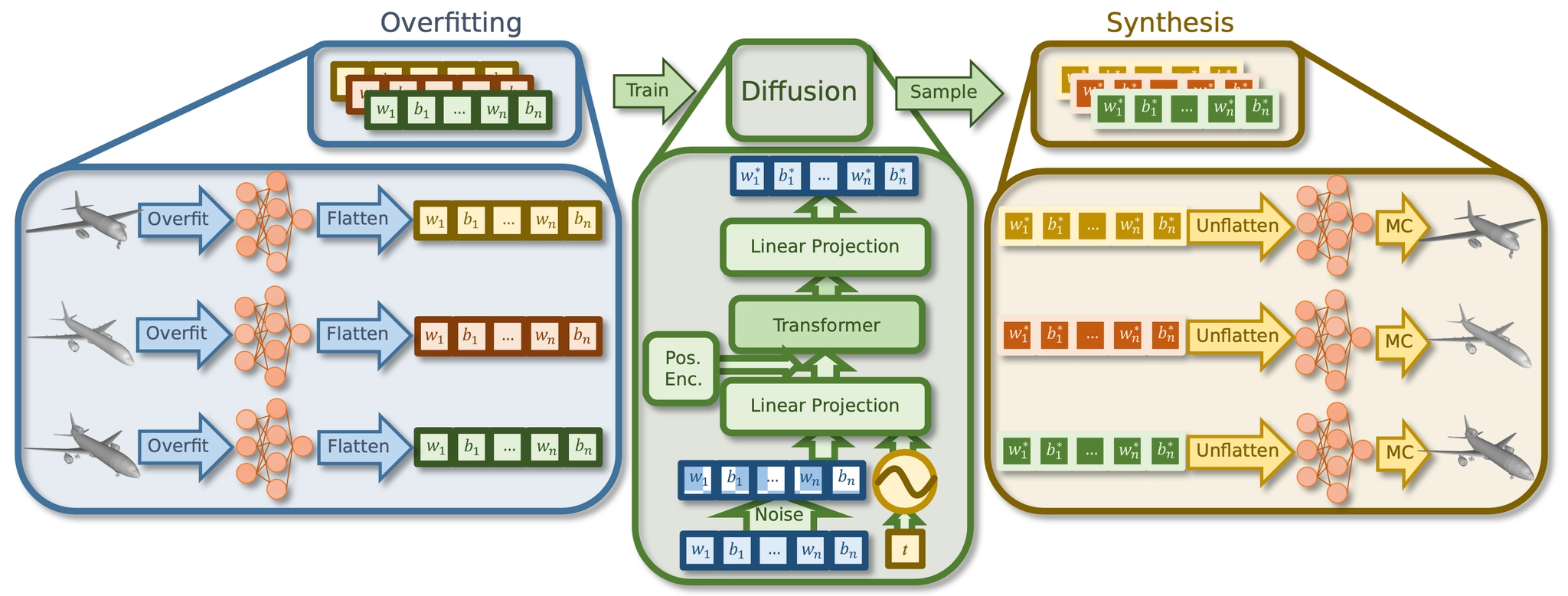
Overview of HyperDiffusion
HyperDiffusion 의 큰 그림은 위 그림과 같습니다. 크게 (1) occupacny field 를 overfitting 하고, 잘 학습된 MLP 의 weight 를 flatten 하여 1 dimensional vector 로 flatten 하는 단계, (2) 1 dimensional weight vector 를 입력으로 하는 Diffusion Model 을 학습하는 단계, (3) 학습된 Diffusion Model 에 임의로 sampling 한 noise 를 입력으로 하여 weight vector 를 생성하고 unflatten 하여 MLP 및 Implicit Neural Field 를 구성하는 단계 로 나누어져 있습니다.
이렇게 하면 Implicit Neural Field 만을 생성할 수 있지만, 3D 및 4D 생성의 경우 Marching Cube 를 사용하여 underlying mesh 를 뽑아내고 시각화하는 것까지 논문에서 언급합니다. 개인적인 생각으로는 기본적인 Marching Cube 방법론을 사용하여 mesh 를 export 를 해도 어느정도 성능이 나올정도로 Implicit Nerual Field 가 정교하게 생성이 되었다- 를 주장하고 싶은 것 같습니다.
Per-Sample MLP Overfitting
논문에서는 학습 데이터로 사용할 weight 를 만들기 위해서 training sample 별로 MLP 를 optimize 하는 과정을 진행합니다. 이 때 논문에서는 occupancy 를 기반으로 한 MLP 를 학습합니다. 다만 여타 classification (여기서는 occupied 와 non-occupied 를 나누는 것) 과 같이 Softmax 등을 사용해 0 ~ 1 사이의 값으로 그 여부를 산출하게 되고 특정 sample data 에 대해서 occupancy 의 정도에 따라 다음과 같이 surface 의 iso-level 을 정의할 수 있다고 합니다.
는 parameters 에 의해서 parameterize 된, 학습하고자 하는 MLP 입니다. 앞서 classification 을 언급했는데, occupancy 를 기반으로 하기 때문에 학습에 사용된 loss 도 binary cross entropy 를 사용합니다.
위 식에서 는 위치 에서 sample 에 대한 ground truth occupancy 를 나타냅니다. 논문에서는 결국 이 단계에서 position 에 따른 occupancy 를 나타내는 ground truth 데이터들을 이용해 각 sample 마다 동일한 구조를 가지는 MLP 네트워크들이 해당 occupancy 를 산출할 수 있도록 각각 optimize 합니다. 이는 Implicit Neural Field 가 가지는 representation power 에 기대어 기존 ground truth 데이터의 형태를 변형했다고 해석하셔도 좋습니다.
여담으로, 논문에서는 이렇게 각 데이터마다 따로 MLP 를 optimize 하는 것이 MLP 의 표현력을 온전히 하나의 데이터를 표현하는 것에 사용할 수 있기 때문에 높은 fidelity 를 가진 표현을 얻어낼 수 있었다고 첨언합니다.
MLP Architecture and Training
논문에서는 MLP architecture 로 가장 기본적인, 3 hidden layers with 128 neurons each 를 사용했습니다. 이 떄 input 에 positional encoding 을 넣어 representation power 를 높이고, 3D 와 4D format 을 모두 사용할 수 있도록 했습니다.
하나의 MLP 를 학습함에 있어서, 3D shape 을 먼저 의 범위로 제한한 뒤에, 의 point 를 전체 bounding box 범위 내에서 임의로 sampling 하고, surface 근처에서 의 point 를 추가적으로 sampling 하여 이를 데이터로 학습을 진행합니다. Suface 근처에서 sampling 하는 것은 fine-scale surface detail 을 챙기기 위한 목적이었다고 합니다. 더불어 MLP 는 2048 개의 점들을 mini-batch 로 하여 BCE loss 로 800 epoch 을 학습했고, 각 shape 마다 optimization 에 6 분의 시간이 소요되었다고 합니다.
4D 를 학습하는 것은 3D 와 큰 차이가 없이 각 frame 마다 의 point 를 sampling 합니다. 각 frame 마다 다른 MLP 를 학습하는 것이 아닌, time 과 함께 네트워크의 입력으로 주어 하나의 MLP 를 학습하게 되는 것이며, 앞서 언급했던 것처럼 positional encoding 단에서 3D 와의 dimension mismatch 문제를 다룰 수 있습니다.
Weight Initialization
논문에서는 diffusion process 의 원활한 학습을 위해서 특별한 weight initialization 을 사용합니다. Training sample 들에 대해서 첫 번째 sample 인 에 대한 MLP parameter 를 학습하고 나서, 나머지 MLP 를 학습할 때 이미 최적화된 을 다른 MLP parameters 의 weight initialization 으로 사용합니다. 구체적인 설명을 해주지는 않지만, variation 을 제한하는 용도로 사용하여 diffusion 에서 쉽게 학습 (overfitting) 할 수 있게 한 것이 아닌가라는 개인적인 생각이 있습니다.
MLP Weight-Space Diffusion
논문에서는 MLP 의 parameter 를 1 dimensional vector 로 flatten 하고 이를 Diffusion Model 을 학습하는데 사용합니다. Diffusion Model 의 denoising network 로 기본적인 U-Net 을 사용하지 않고, transformer architecture 를 사용하는 를 사용했다고 합니다.
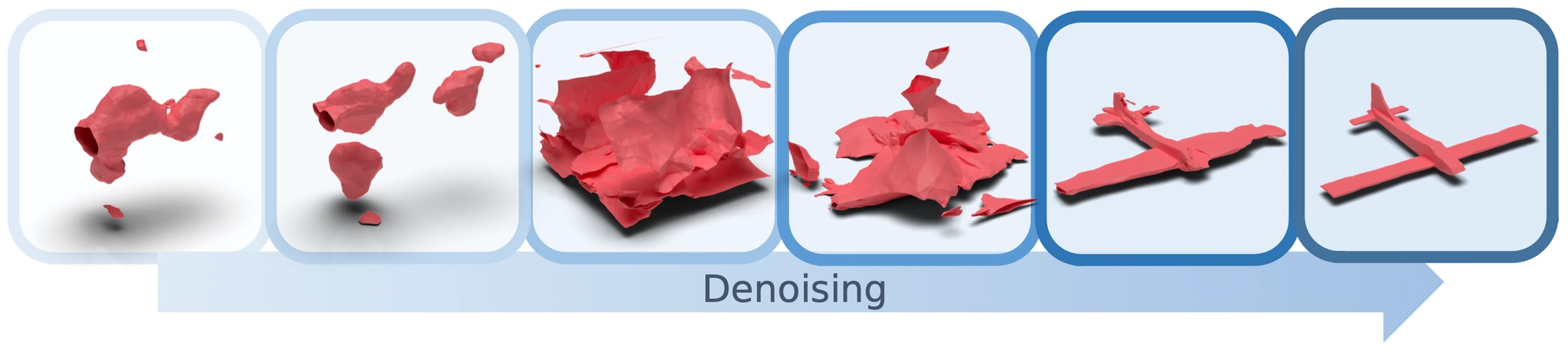
Visualization of Denoising Process of HyperDiffusion
앞서도 언급하지만, 논문에서는 이렇게 MLP 의 parameters 를 diffusion process 의 입력 및 출력으로 사용하는 세팅은 다양한 dimension 의 입력에 대해서도 동일하게 동작할 수 있도록 했고, 논문의 경우에는 3D 와 4D 를 동시에 다루게 해준 요인이라고 강조합니다.
논문의 Diffusion Model 은 MLP 의 parameters 를 사용하는데, 직접적으로 여기에 noise 를 더한 뒤 이를 denoising network 의 input 으로 사용하진 않습니다. 논문에서는 noise 를 번 더한 MLP parameters 와 를 sinusoidal embedding 한 값을 linear projection layer (MLP) 를 거쳐 8 개의 token 으로 만든 뒤, learnable positional encoding vector 와 더해 denoising network 의 입력을 만들어냅니다.
Denoising network 는 해당 입력을 받아 denoised token 을 출력해내고, 이를 다시 linear projection layer (another MLP) 를 통과시켜 MLP 의 parameters 를 다시 복원해내고, 복원해낸 값과 실제 MLP parameters 와의 MSE loss 를 통해 학습이 진행됩니다. 이렇게 학습을 진행할 경우, 위의 그림과 같이 denoising step 에 따라서 예측한 MLP parameters 로 시각화한 형태가 점점 그럴듯해짐을 살펴볼 수 있습니다.
Implementation Details
크게 중요한 부분은 아니지만, 논문에서는 Diffusion Model 을 학습할 때 다음과 같은 implementation setting 을 사용했다고 합니다. 이는 관심이 있으신 분들이 살펴보시면 좋을 것 같습니다.
Implementation Settings
Experiments
Datasets
3D Shape Generation task 를 수행할 때, 논문에서는 ShapeNet dataset 의 Car, Chair, Airplane 카테고리를 사용했고, 4D Shape Generation task 를 수행할 때, DeformingThings4D dataset 의 animal animation sequence 의 16 프레임을 사용했습니다. 각각의 데이터셋에서 겹치는 데이터 없이 80%, 5%, 15% 를 각각 training, validation, test 에 사용했다고 합니다.
Voxel-based Diffusion Baseline
많은 기존의 연구들이 3D Shape Generation 만을 타겟팅하여 unconditional 4D Shape Generation 은 여전히 비교할 대상이 부족한 관계로, 논문에서는 비교할 baseline 으로 직접 구현한, Voxel-based Diffusion Model 을 선택합니다.
Voxel-based Diffusion Model 에서 3D Shape 은 밀도가 높은 occupancy grid 의 표현 방법을 사용하고, 3D U-Net 이 3D Voxel 의 denoising 을 위해 사용됩니다. 4D 의 경우에는 3D 와 동일하게 각 frame 별로 학습을 진행해서 이어붙이는 방법을 채택합니다. 이에 대한 이유로 4D UNet 이 computationally intractable 했기 때문이라고 밝힙니다. 구체적으로는 이러한 computation 을 고려하여 3D 에서는 크기의 voxel resolution 을, 4D 에서는 의 resolution 을 선택합니다.
Evaluation Metrics
3D 와 4D 의 unconditional shape synthesis 는 직접적으로 비교할 ground truth data 의 부재로 평가가 어렵습니다. 논문에서는 선행연구들에서 비교한 방법들을 그대로 채용하고, 그것들은 Minium Matching Distance (MMD), Coverage (COV), 그리고 1-Nearest-Neighbor Accuracy (1-NNA) 입니다.
위 의 는 generated dataset 과 reference dataset 의 합집항 중 와 가장 유사한 데이터 (거리가 짧은 데이터) 를 의미합니다. 구체적인 수식은 다음과 같습니다.
여기서 위 식에서와 , 의 정의 모두에서 쓰인 거리 함수 는 chamfer distance 로 정의가 되며 정확히는 해당 값에 을 곱한 값이며, 4D 의 경우에는 각 frame 별 의 평균으로 다음과 같습니다.
논문에서는 metric 이 [Zeng et al. 2022] 에서 generation quality 를 대변해주지는 못한다는 사실을 적시하고 있으며, 이에 따라 일반적인 domain 간의 유사도를 평가하는 지표인 FID 와 유사한 개념인 Frechet Pointnet++ Distance 를 평가지표로 추가로 사용했다고 합니다. 이는 ModelNet 에서 학습된 3D Pointnet++ Network 로 feature extracion 을 진행하여 계산한다고 합니다.
평가에 있어서, 생성된 shape 과 ground truth dataset 의 shape 모두 각 shape 이 가지는 mean 과 standard deviation 로 normalize 를 진행했고, point 기반의 비교에서는 2048 개의 point 를 임의로 sampling 했다고 합니다. 이 때 논문의 방법론과 voxel baseline 은 surface 의 표면에서, point cloud baseline 은 synthesized output 자체에서 sampling 을 진행합니다.
Unconditional 3D Generation
논문에서는 먼저 3D Shape Generation 을 위해 HyperDiffusion 을 사용한 경우에 대한 실험 결과를 보여줍니다. 논문의 방법론은 Implicit Neural Fields 를 생성하기 때문에 Marching Cube 를 사용하여 output mesh 를 생성합니다.
Comparison to SOTA
3D Shape Generation task 에서는 SOTA 를 보여주는 Point-Voxel Diffusion , Diffusion Point Cloud , 그리고 앞서 논문에서 구현한 Voxel Baseline 과의 정량적인 비교를 제시합니다.
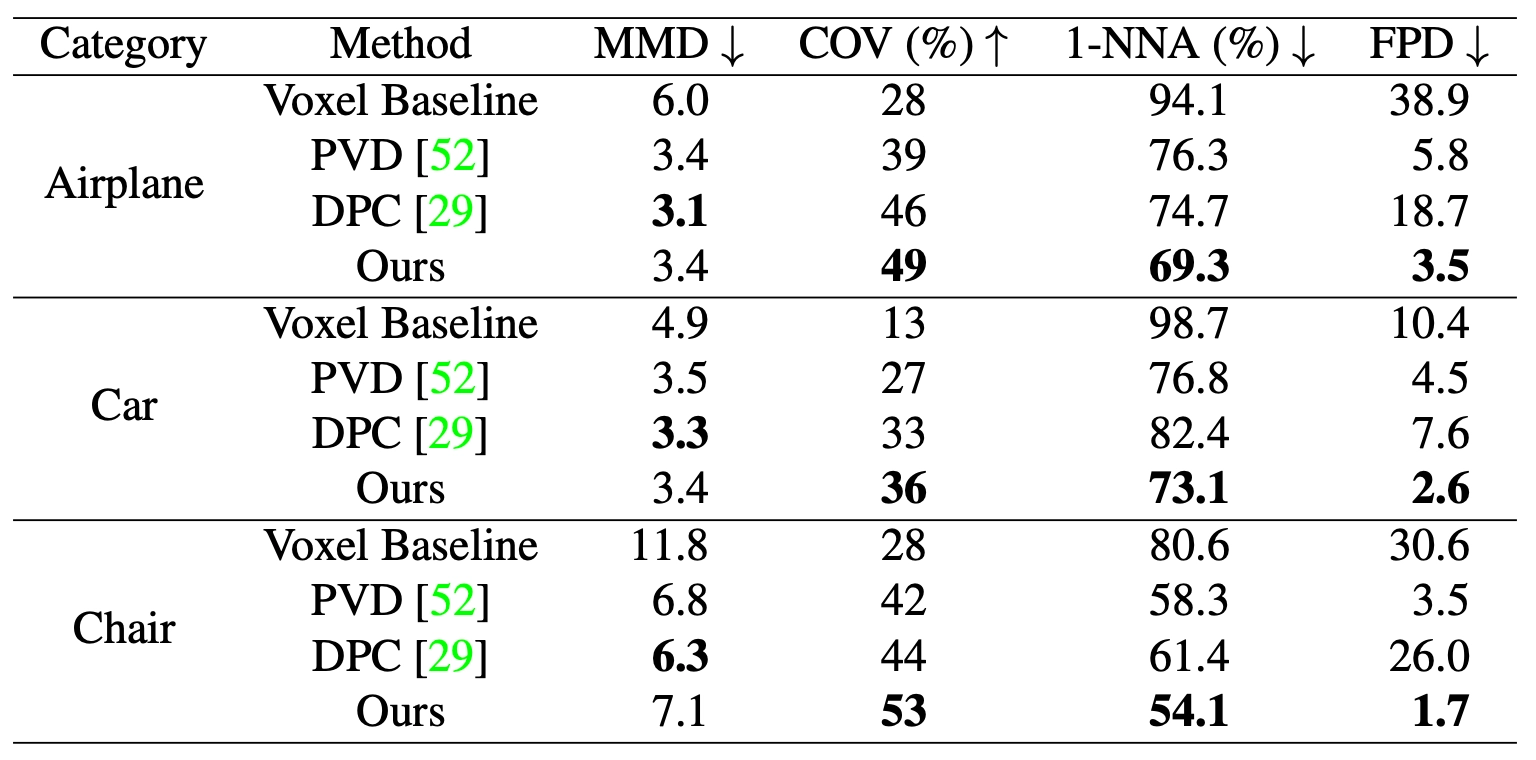
Quantitative Comparison on Unconditional 3D Shape Generation
HyperDiffusion 은 모든 shape 카테고리와 를 제외한 모든 평가지표에서 다른 baseline 보다 우수한 지표를 보여주었습니다. 그리고 는 앞선 논문에서 지적된 바와 같이 낮은 품질의 결과에 대한 민감도를 가지지 않는 지표라는 것을 이야기하며 해당 지표에서 좋지 못한 결과를 얻은 것이 성능이 좋지 못하다는 것을 시사할 순 없다고 합니다. 이렇게 이야기하면서, HyperDiffusion 이 특히 인간이 지각하는 품질에 큰 관련이 있는 지표에 큰 개선이 있었다는 점을 강조합니다.
Qualitative Comparison for 3D Shape Generation
위 그림은 논문에서 제시한 정성적인 3D Shape Generation 결과입니다. 해당 이미지를 통해 다른 비교 baseline 들에 비해서 geometric detail 을 더 잘 묘사할 수 있음을 보여주었습니다.
Effect of Overfitting Weight Initialization
논문에서는 MLP 를 optimize 할 때, 가지고 있는 training sample 별로 random initialization 을 택하지 않고, 첫 sample 의 optimized 된 weight 를 나머지 sample 들의 initialization 으로 택합니다. 이러한 방법론의 유의미함을 보이기 위해서 다음과 같은 ablation 결과를 보여줍니다.
Ablation on Weight Initialization for 3D Shape Generation (Airplanes)
각각의 training sample 별로 random initialization 한 결과와 정량적인 지표를 비교했으며, Overfitting Weight Initialization 을 시행한 쪽이 신뢰성이 떨어지는 를 제외하고 모든 지표에서 더 나은 지표를 보여주었습니다. 이러한 지표의 상향은 동일한 initialization 을 취했을 때 MLP weight 가 상대적으로 서로 가깝게 학습되도록 한다는 사실에 기인한 것으로 보고 있다고 합니다.
Effect of MLP Positional Encoding
논문에서는 denoising network 의 입력을 만들기 위해서 linear projection 으로 생성된 token 에 learnable positional encoding 을 더하는 과정을 진행합니다. 논문에서는 이러한 설계의 유의미함을 보이기 위해서 다음과 같은 ablation 결과를 보여줍니다.
Ablation on Positional Encoding in the MLP for 3D Shape Generation (Airplanes)
위 표에서 살펴볼 수 있듯이 모든 지표에서 positional encoding 을 넣었을 때 더 좋은 결과를 보여줍니다. 논문에서 설명하지는 않지만 어느정도 당연하게도, permutation equivalent 한 특성을 가지는 transformer 에 순서가 존재하는 layer 의 weight 가 들어가는 것이기 때문에 positional encoding 을 넣는 것이 도움이 되었다고 볼 수 있을 것 같습니다.
Novel Shape Synthesis
논문에서는 HyperDiffusion 이 training dataset 의 구조를 단순히 외우는 것이 아니라 새로운 형태를 생성할 수 있음을 보여줍니다.
Novel Shape Generation w/ Nearest Neighbor Retrieval
위 그림의 붉은색 shape 은 HyperDiffusion 으로 생성해낸 것이고, 초록색 shape 들은 붉은색 shape 과 chamfer distance 가 가장 낮은 3 개의 nearest neighbors 입니다. 이들이 서로 유의미하게 다름을 통해 논문에서는 diffusion 을 통해 network weight 를 학습하는 과정이 3D mesh 상에서의 data distribution 을 일반적으로 학습할 수 있다고 주장합니다.
Unconditional 4D Generation
HyperDiffusion 이 임의의 dimension 의 데이터에 대한 lmppcit Neural Fields 를 생성해낼 수 있기 때문에, 논문에서는 4D 데이터를 사용하는 Implicit Neural Fields 를 생성하는 task 를 실험한 결과를 제공합니다. 기존 3D 에서 time 이라는 dimension 이 하나 추가된 것으로 볼 수 있습니다.
Quantitative Evaluation of 4D Unconditional Generation
위 표는 정량적인 지표를 가지고 논문의 Voxel Baseline 과 비교한 결과입니다. Dimension 의 증가에 빠르게 성능 저하가 나타난 Voxel Baseline 과는 달리 HyperDiffusion 은 성능을 어느정도 유지하는 모습을 보여주었습니다.
Qualitative Comparison of 4D Animation Syntheis
위 그림은 논문에서 제시한 정성적인 4D animation 생성 결과입니다. 논문에서는 HyperDiffusion 의 animation 결과가 Voxel Diffusion 의 결과에 비해서 각 시점마다 자연스러운 temporal consistency 를 보여준다고 이야기합니다. 더불어 animation 도중에 shape integrity 도 유지할 수 있었다는 것을 보여줍니다.
Conclusion
이것으로 논문 “HyperDiffusion: Generating Implicit Neural Fields with Weight-Space Diffusion” 의 내용을 간단하게 요약해보았습니다.
이 논문은 사실 3D Shape Generation 의 결과 자체보다는 Weight-Space Diffusion 이라는 신박한 개념과 4D Shape Generation 의 결과에 이끌려서 관심을 가졌던 논문이었는데, 크게 복잡하지 않은 구조와 개념으로 좋은 결과를 뽑아낸 논문이라고 느꼈던 것 같습니다.
다만 4D 의 학습에 대해서 논문 내에서 구체적으로 설명해주지 아쉬웠고, 구체적으로는 3D 의 경우에는 카테고리를 나누어 학습했다고 명시해주었는데 4D 에서는 action 별로 카테고리를 나누는지 shape 별로 카테고리를 나누는지 둘 모두가 동일한 범주 내의 데이터로 카테고리를 나누는지에 대해서 전혀 설명이 없어서 이해하기 어려웠습니다. 개인적인 생각으로는 action 을 카테고리를 나누지 않으면 깔끔하게 존재하는 (그럴듯한) action 들만 생성되지는 않을 것 같아 action 은 카테고리별로 학습했을 것 같은데, shape 은 데이터셋을 어느정도 memorize 하고 variation 을 줄 수 있으면 가능해보이기도 해서 아직은 잘 모르겠습니다. 다만, 결과가 생각보다 좋아서 shape 도 카테고리를 나눈 것일 가능성이 좀 높다고 생각이 듭니다. 자세한 것은 코드의 공개나 아래의 데이터셋을 살펴보면 좋을 것 같습니다.
이 논문은 제가 4D 나 Free Viewpoint Video 등 time variant 에 대해서도 관심을 가지게 한 첫 논문이라 의미가 깊은 것 같습니다. Diffusion 에 대한 prior knowledge 가 어느정도 있으시고, 4D 에 관심을 가지신 분이 읽으시면 좋을 것 같다는 생각이 듭니다.