본 포스트에서는 View Synthesis 분야에서 새로운 방법론을 제시한 논문에 대해서 소개드리려고 합니다. 리뷰하려는 논문의 제목은 다음과 같습니다.
“NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis”
Objective
View Synthesis 는 주어진 다양한 카메라각에서의 image view 를 바탕으로 랜덤한 카메라각에서의 image view 를 생성해내는 task 입니다.
위 그림과 같이 하나의 object 에 대해서 다양한 카메라 각에서의 input image 가 주어졌을 때, 해당 object 의 랜덤한 각에서의 view 를 생성하는 작업이라고 보시면 됩니다.
기존에 View Synthesis 를 구현하는 주된 방법론은 Neural 3D shape representations 였습니다. 이는 x, y, z coordinate 좌표를 signed distance functions 또는 occupancy fields 로 매핑하는 네트워크를 학습하여 implicit 한 3D shape 를 구현해내는 방법이었습니다. 하지만, 이러한 방법론은 실제로 매우 복잡한 기하학적 구조를 가진 물체의 view 를 형성하는 성능이 좋지 못했고 최종적으로 렌더링된 이미지는 oversmooth 된 형태를 가지기 마련이었습니다. 더불어, 학습한 네트워크를 바탕으로 원하는 방향에서의 scene 을 형성하기 위해서도 discrete sampling 과정이 필요했기 때문에 시간 및 공간 복잡도 측면에서도 그닥 좋지 못했다고 합니다.
논문에서는 위 두 가지 문제점을 동시에 해결할 수 있는 새로운 방법론인 Neural Radiance Field Scene Representation 를 제시합니다.
Neural Radiance Field Scene Representation
논문에서는 해당 문제를 다루기 위해서 Neural Radiance Field 라고 불리는 특별한 필드를 정의합니다.
이는 input 으로 3D 위치 정보 () 와 camera direction () 를 받고 output 으로 검출된 색상과 volume densitiy 를 반환하는 5D vector-valued function 입니다.
Volume Density 란?
특정 위치의 object 혹은 위치 자체의 특성이 camera view 에 얼마나 기여하는지를 나타내는 척도라고 보시면 됩니다. 실제로, camera view 와 실제 object 의 위치 정보 사이의 ray 상에는 다양한 점들이 존재하고, 이 점들 각각이 주는 영향이 모여서 camera view 를 형성하게 된다는 직관에서 나온 값입니다. Density 가 높을수록 camera view 에 영향을 많이 준다- 로 해석하시면 됩니다.
이렇게 정의한 Nerual Radiance Field 는 다음과 같이 표현할 수 있습니다.
는 3D 좌표, 는 direction, 는 색상 정보 (red, blue, green), 는 volume density 를 나타냅니다.
논문에서는 이렇게 정의한 Field 자체를 논문에서 제시한 MLP 네트워크와 동일시하는 방법론을 제시했고, 이를 통해 학습 과정 자체가 어떤 하나의 object 에 대해서 Neural Radiance Field 를 완성하는 과정이며 완성된 Neural Radiance Field 에 원하는 3D 좌표와 direction 을 넣음으로써 랜덤한 카메라각에서의 view 를 얻어낼 수 있도록 설계합니다.
학습과정 자체를 정의한 Neural Radiance Field 를 완성시키는 과정이자 3차원 object 에 대한 volume rendering 과정으로 본다는 것입니다.
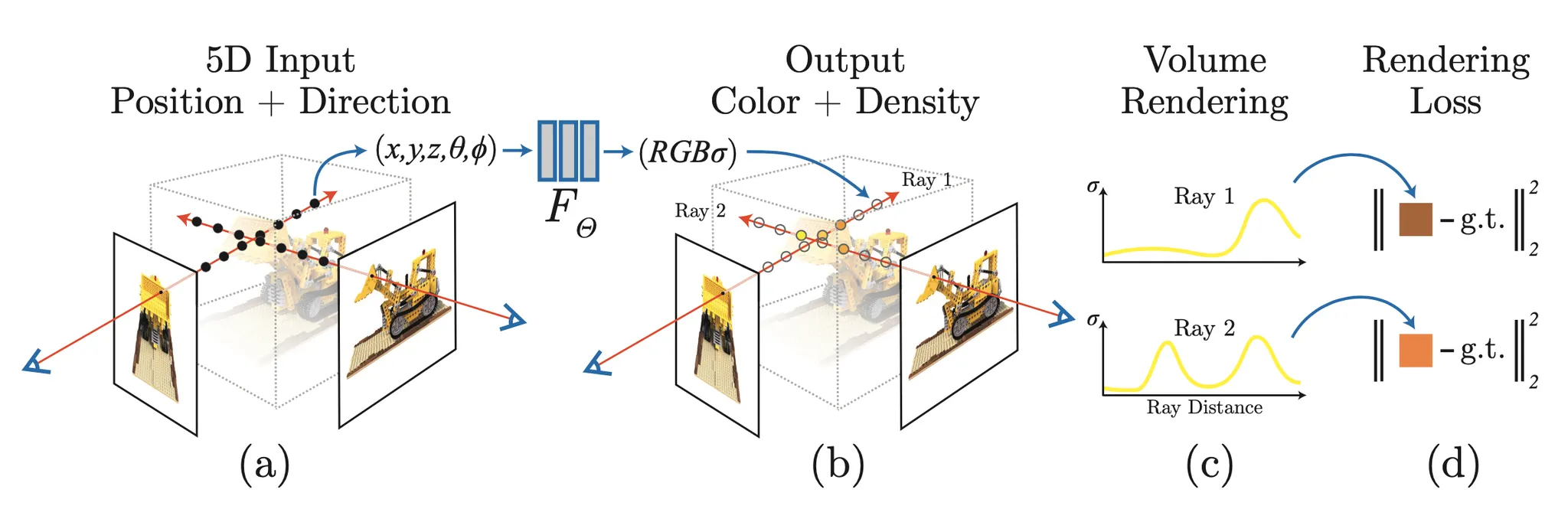
논문에서는 위의 그림과 같은 플로우로 View Synthesis 과정을 설계합니다. 특정 물체에 대한 다양한 카메라각에서의 Ground Truth 이미지 및 데이터를 준비하고, 하나의 이미지를 구성하는 빛의 선 (Ray) 위의 다양한 좌표들의 묶음 및 각도를 input dataset 으로 활용하고, 네트워크를 거쳐서 최종적인 R, G, B 및 volume density 를 뽑아낸 뒤에 뽑아낸 데이터들을 바탕으로 최종적인 색상을 예측하고 해당 Ray 가 실제로 이미지 위의 어느 픽셀에 대응되는지 매칭한 픽셀의 색상과 비교하여 Loss 를 계산한 뒤에 Gradient Descent 를 사용해 학습을 진행합니다.
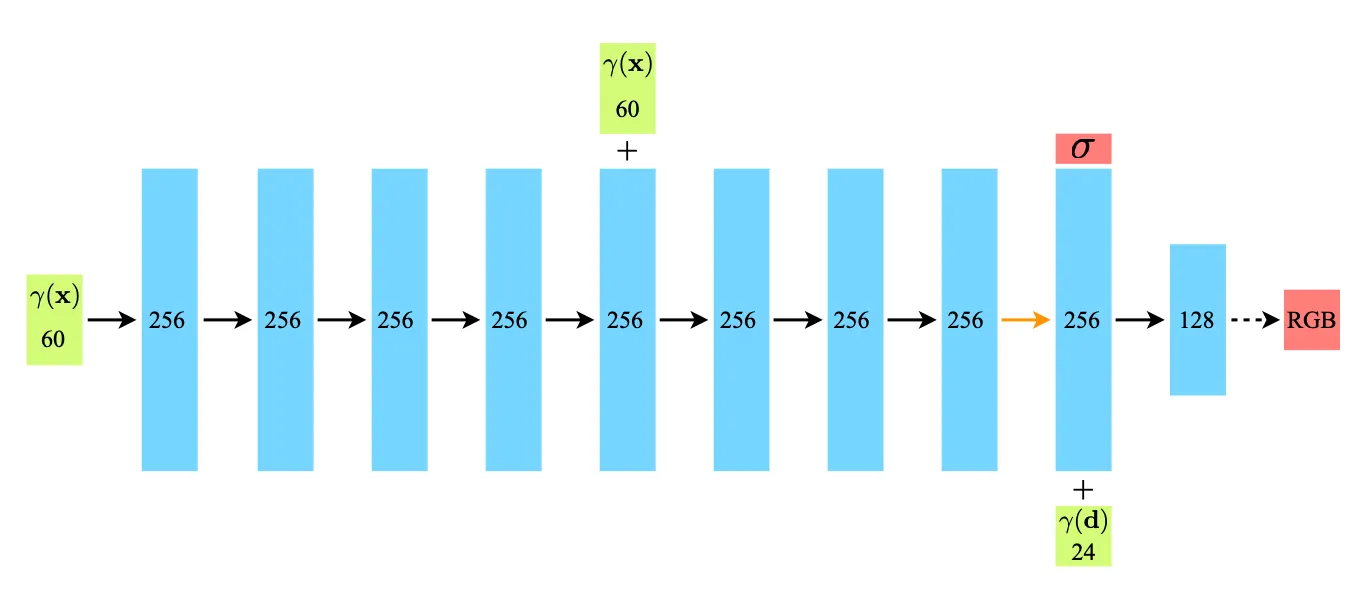
놀랍게도, 이 일련의 과정을 논문에서는 MLP 로만 구현해냅니다. 아래 사진은 논문의 Additional Implementation Details 에서 가져온 논문의 대략적인 네트워크 구조입니다.
논문에서는 3D 좌표 정보 를 넣고 8 개의 Fully-Connected Layer 를 통과시킨 뒤에 Volume Density 와 feature vector 들을 출력해냅니다. 그리고 출력한 feature vector 와 새로 들어온 direction 정보 를 concatenate 한 뒤 다시 하나의 Fully-Connected Layer 를 통과시켜 RGB 색상 데이터를 출력해냅니다.
이 구조를 보시면 눈치 빠르신 분들은 의문을 품으실 수 있습니다. Volume Density 가 direction 에 의존한 출력값이 아닌 것 처럼 보이기 때문입니다. 결론부터 말씀드리자면 의존한 출력값이 아닌 것이 맞습니다. 논문에서는 Volume Density 를 direction 에 무관한 요소로 정의해버립니다. 어떤 위치 자체가 view 에 주는 영향이 카메라각에 영향을 받지 않는다는 가정을 도입한 것입니다. 개인적으로 요 부분은 편광필름처럼 방향에 따라 빛의 투과성이 달라지는 물질로 이루어진다면 무리가 있을 가정으로 보이긴 하는데, 일반적으로 그러한 특성을 가지는 물질이 적고 학습 목표를 간소화하는데 도움이 있어서 사용하지 않았나 생각해봅니다.
Volume Rendering with Radiance Fields
이미지의 한 색상을 구성하는 것은 Ray 의 어느 한 지점이 아니라 Ray 상의 모든 지점들의 영향이 합쳐진 효과입니다. 이를 고려한 것이 기존의 Classical 한 Volume Rendering 방법으로 다음과 같습니다.
Ray 를 정의하는 near bound , far bound 에 대해서 최종적인 색상 예측은
와 같이 표현할 수 있습니다.
위 식에서 와 부분이 네트워크가 산출해내는 색상 예측값이라고 보시면 됩니다. 위치의 좌표와 Ray direction 이 input 으로 들어가 색상 값을 산출해내고, Volume Density 는 위에서 언급했듯이 위치의 좌표만으로 산출된 값이라고 보시면 됩니다. 따라서, Ray 를 따라서 존재하는 위치들의 색상과 그 Volume Density 를 마치 weighted sum 처럼 적분하여 계산한 것으로 보시면 됩니다.
여기서 설명드리지 않은 특정 좌표가 색상에 미치는 값이 view 와 그 좌표 사이에 존재하는 좌표들의 종합적인 투과도입니다. 이를 간단히 설명드리자면, 특정 카메라각에서 특정 좌표가 이미지의 색상에 미치는 값을 판단하려고 할 때 그 좌표만의 Volume Density 뿐만이 아니라 view 와 좌표 사이에 존재하는 좌표들이 얼마나 투과성이 좋은지에 대한 정보도 추가적으로 정의한 것입니다. 즉, 투과성이 좋으면 좋을수록 해당 좌표가 이미지의 색상에 미치는 영향이 크다는 점을 반영한 값이라고 보시면 됩니다.
위 식에서도 볼 수 있듯이, view 에서 가까운 쪽으로 부터 해당 좌표까지만큼의 Volume Density 를 적분한 값의 inverse exponential 값입니다. Volume Density 가 얼마나 영향력이 있냐! 로 앞에서 설명드렸었는데 이에 대략적으로 반대되는 개념으로 보실 수 있습니다. 앞의 좌표들이 얼마나 영향력이 없어서 (투과성이 좋아서) 해당 좌표가 영향력을 행사할 수 있을 것이냐- 에 대한 값인 것입니다.
이렇게 하나의 Ray 위에 존재하는 다양한 좌표들 각각에 대해서 네트워크를 통과시키고 (실제로는 이들을 하나의 Batch 로 묶어서 학습을 진행할 것으로 예상해봅니다-) 예측한 값들을 바탕으로 최종적인 이미지의 색상을 예상하는 전통적인 Volume Rendering 방법에 대해서 설명드렸습니다. 하지만, 실제로 Ray 위의 모든 좌표들을 이용해 적분을 통해서 해당 값을 구하는 것은 불가능하기 때문에 논문에서는 Ray 위의 값들 중 일부를 sampling 하여 사용하게 됩니다. (논문에서는 query 라는 용어를 사용했습니다.)
위 식은 Ray 의 의 구간을 개의 partition 으로 나눈 뒤, 각각의 partition 에서 하나의 를 선택 (sampling) 하되, uniform distribution 을 가정하고 하나씩 좌표를 뽑는 방법입니다. 이렇게 discrete 한 좌표를 하나씩 선택하게 되고, 해당 좌표 가 주어졌을 때 네트워크가 산출해낸 색상 및 Volume Density 를 각각 라고 하고, 라고 했을 때 Color Estimation 은 다음과 같이 표현할 수 있게 됩니다.
여기서 또한 discrete case 에 대해서 를 각 sample 사이의 구간별 Volume Density 의 대푯값으로 생각하여 다음과 같이 정의할 수 있습니다.
이 때, 논문에서 Max et al. 을 레퍼런스 삼아 부분을 다음과 같은 변경하여 최종적인 Color Estimation 을 정의합니다. 가 커짐에 따라서 가중치가 높아지는 양상은 이전과 동일한 것을 확인할 수 있습니다.
레퍼런스 논문에 대한 정보는 아래에서 확인하실 수 있습니다. 정확한 변경이 가져다 주는 이점에 대해서는 아래 논문에서 확인해보시는 것을 추천드립니다. (저는 확인해보지는 않았어요.)
Optical models for direct volume rendering
This tutorial survey paper reviews several different models for light interaction with volume densities of absorbing, glowing, reflecting, and/or scattering material. They are, in order of increasing realism, absorption only, emission only, emission and absorption combined, single scattering of external illumination without shadows, single scattering with shadows, and multiple scattering.
https://ieeexplore.ieee.org/document/468400
Max, N.: Optical models for direct volume rendering. IEEE Transactions on Visualization and Computer Graphics (1995)
Optimizing a Neural Radiance Field
앞서는 논문에서 View Synthesis 를 구현하기 위해 골자로 사용했던 네트워크 및 방법론에 대해서 소개를 드렸습니다. 하지만, 위의 방법만으로는 해당 분야에서 SOTA 를 달성할 수 없었기 때문에 논문에서는 고해상도의 복잡한 scene 에 대해서도 잘 동작할 수 있도록하는 두 가지 개선안을 제시했습니다.
Positional Encoding
첫 번째로 논문에서 발견한 문제점은 Rahaman et al. 에서도 동일하게 언급했던 현상인 네트워크가 low frequency function 을 학습한다는 점입니다. 즉, 색상이나 모양이 복잡하게 얽혀져 있는 object 에 대한 성능이 낮았다는 것입니다. 해당 레퍼런스 논문에서는 네트워크에 데이터를 넣기 전에 데이터를 고차원으로 mapping 하는 작업이 high frequency variation 을 가질 수 있도록 하는데 도움을 준다는 결론이 있었고, 논문에서는 해당 사항을 참고하여 3D 좌표 데이터와 direction 데이터를 바로 넣지 않고 고차원 데이터로 dimension 매핑을 진행합니다.
각각의 좌표 에 대해서 다음과 같은 mapping 을 시행하고 이에 따라서 input data 가 배 만큼의 dimension 이 증가하게 됩니다. 3D 좌표와 마찬가지로 direction 도 로 표현된 것을 3D directional vector 로 변환할 수 있으며 같은 과정을 거쳐 배 만큼의 dimension 이 증가를 얻어낼 수 있습니다.
실제 논문에서는 에 대해서는 을, 에 대해서는 를 사용하여 각각 60-dimension vector 와 24-dimension vector 를 사용했다고 합니다.
Hierarchical Volume Sampling
두 번째로 논문에서 발견한 문제점은 Ray 상에서 N 개의 좌표를 sampling 하여 최종적인 Color Estimation 을 하는 과정이 효율적이지 못했다는 점입니다. 실제로 아무 것도 없는 좌표 및 막혀서 이미지의 뷰에 영향을 줄 수 없는 좌표가 지속적으로 sampling 되어 이미지의 뷰에 영향을 주었고 성능면에서 좋은 현상으로 보지 않았습니다.
이를 해결하기 위해 논문에서는 학습에서 두 가지 네트워크를 동시에 학습하도록 변경합니다. 첫 번째 네트워크를 Coarse Network 로, 두 번째 네트워크를 Fine Network 라 명칭하고, Coarse Network 의 학습은 개의 sample 좌표를 뽑아서 이전과 동일하게 진행합니다. 학습을 진행하게 되면 각 좌표에 대한 estimation 값들 ()을 다음과 같이 구해낼 수 있습니다. 이 때, 의 가중치 항목으로 이전에 정의했던 부분을 묶어 로 칭하고 해당 부분에 대한 값들을 각 좌표별로 정의해낼 수 있게 됩니다.
이 때 얻어낸 들을 를 사용해 normalize 를 하게된다면, 구간별로 constant 인 PDF 를 얻게 됩니다. 여기서 논문에서는 inverse transform sampling 을 사용하여 높은 weight 를 가진 구간에서의 값이 더 잘 sampling 되도록 다시 한 번 개의 좌표를 sampling 합니다. 이렇게 다시 한 번 개의 sample 로 Color Estimation 을 진행한 값으로 loss 를 구하고 학습을 진행합니다. 이렇게 설계함으로써 Coarse Network 에서 높은 확률로 이미지에 영향을 줄 것으로 생각했던 부분에 한 번 더 가중치를 두어 sampling 하는 효과를 얻게되어 기존의 문제점을 어느정도 해결할 수 있었던 것으로 보입니다.
Results
논문에서 제시한 결과를 살펴보기 이전에 이미지의 유사도에 관련된 유명한 metric 에 대한 설명을 간단하게 하려고 합니다.
PSNR (Peak Signal-to-Noise Ratio) 은 이미지 속 노이즈의 비율을 나타내는 척도로 다음과 같이 간단한 MSE 로 계산되는 metric 입니다.
PSNR 는 이미지 픽셀 최댓값 (ex. 8bit gray scale 에서 255) 의 제곱에서 픽셀 값을 기준으로 MSE 를 구한 것을 나누어 logarithm 을 적용한 것이라고 보시면 됩니다.
SSIM (Structural Similarity) 는 PSNR 이 사람이 보기에 비슷한 척도를 반영하지 못한다는 단점을 해결하기 위해 등장한 metric 입니다. (PSNR 이 낮다고 더 유사해보이는 것은 아니라는 점)
위의 는 각각 Luminance (밝기), Contrast (대비), Structure (구조) 를 비교하는 함수이며 각각 다음과 같습니다.
여기서 는 이미지의 luminance, 는 이미지의 contrast 이며 는 상수입니다. 간단한 직관으로 두 이미지의 luminance 와 contrast 가 비슷하다면 해당 항목이 1 에 가까워짐을 알 수 있습니다.
그리고 논문에서는 LPIPS 라는 metric 도 활용하는데, 이는 다른 논문에서 소개한 이미지 유사도에 대한 척도로 보시면 됩니다. 이는 낮을수록 유사한 특성을 가진다고 합니다.
그 결과로 논문에서 다른 네트워크와 비교하여 제시한 결과는 위와 같습니다. 논문의 네트워크 및 방법론이 두 가지 dataset (Diffuse Synthesis 360, Realistic Synthesis 360) 모두에서 가장 좋은 결과를, 논문에서 만든 dataset 에서도 LPIPS 를 제외하고는 가장 좋은 결과를 보여줌을 알 수 있었습니다.
더불어 논문에서는 정성적인 결과를 이미지를 통해서 보여줍니다. 아래는 논문에서 제시한 각 네트워크 별 View Synthesis 결과 이미지입니다.
논문의 방법론이 다른 네트워크와는 달리 범선의 돛대, 레고의 기어와 트레드 등의 기하학적 디테일을 살릴 수 있음을 확인할 수 있었습니다. 논문의 방법론과는 달리 LLFF 는 마이크 스탠드와 물체의 가장자리에서 bading artifact 를 보였고 레고 물체와 범선의 돛대에 ghosting artifact 를 보였습니다. SRN 은 전체적으로 모든 케이스에 대해서 blurry 하고 distorted 된 렌더링을 보였습니다.
마지막으로 논문에서는 네트워크 및 방법론을 디자인할 때 주요하게 선택했던 세부 기획(디자인) 들의 선택이 유효함을 보이기 위해 ablation study 결과를 보여주었습니다.
Positional Encoding, Hierarchical Volume Sampling 의 유무에 따른 성능 비교는 물론 direction 을 input 으로 넣는지의 여부인 View Dependence 에 따른 비교, 이미지의 개수 및 Positional Encoding 에서 사용하는Frequency 를 조절하는 인자의 수준에 따른 비교까지 진행했습니다.
그 결과, Positional Encoding, Hierarchical Volume Sampling 이 존재하는 경우에 대해서 성능지표가 더 좋았으며, direction 도 input 으로 넣었을 때의 학습효과가 더 좋았습니다. 이미지의 개수가 늘어남에 따라 성능도 좋아졌는데, 25 개의 image 만 사용해도 NV, SRN, LLFF 에서 100 개의 image 로 학습을 진행한 것보다 성능이 좋았다고 합니다. Frequency 를 늘리기 위해 L 을 늘리게 될 경우 처음에는 성능이 증가했지만, L 이 너무 커지면 효과가 없음을 알 수 있었고 논문에서는 image 의 최대 frequency 보다 이 커지게 되는 L 부터 효과가 없지 않았나- 라는 직관을 가지고 있다고 합니다.
Conclusion
이것으로 논문 “NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis” 의 내용을 간단하게 요약해보았습니다.
컴퓨터 비전 및 3D 그래픽스에 관심이 있었는데 관련해서 해당 논문이 2020 년도에 꽤나 이슈가 되었다고 하여 주변의 추천으로 읽게 되었던 논문입니다. 확실히 주제 자체가 되게 흥미로웠고 물론 논문에서 구체적인 Ray 의 image 위에서의 pixel 매핑 관련 내용을 서술해주지는 않았지만 큰 골자에서 내용을 이해하기에 크게 어려운 부분은 없었던 것 같습니다.
저랑 비슷한 분야에 흥미를 가지고 계시다면 한 번 읽어보시는 것을 추천드려봅니다.