Gated Recurrent Unit (GRU)

태그
Recurrent Neural Network
포스팅 날짜
2021/10/12
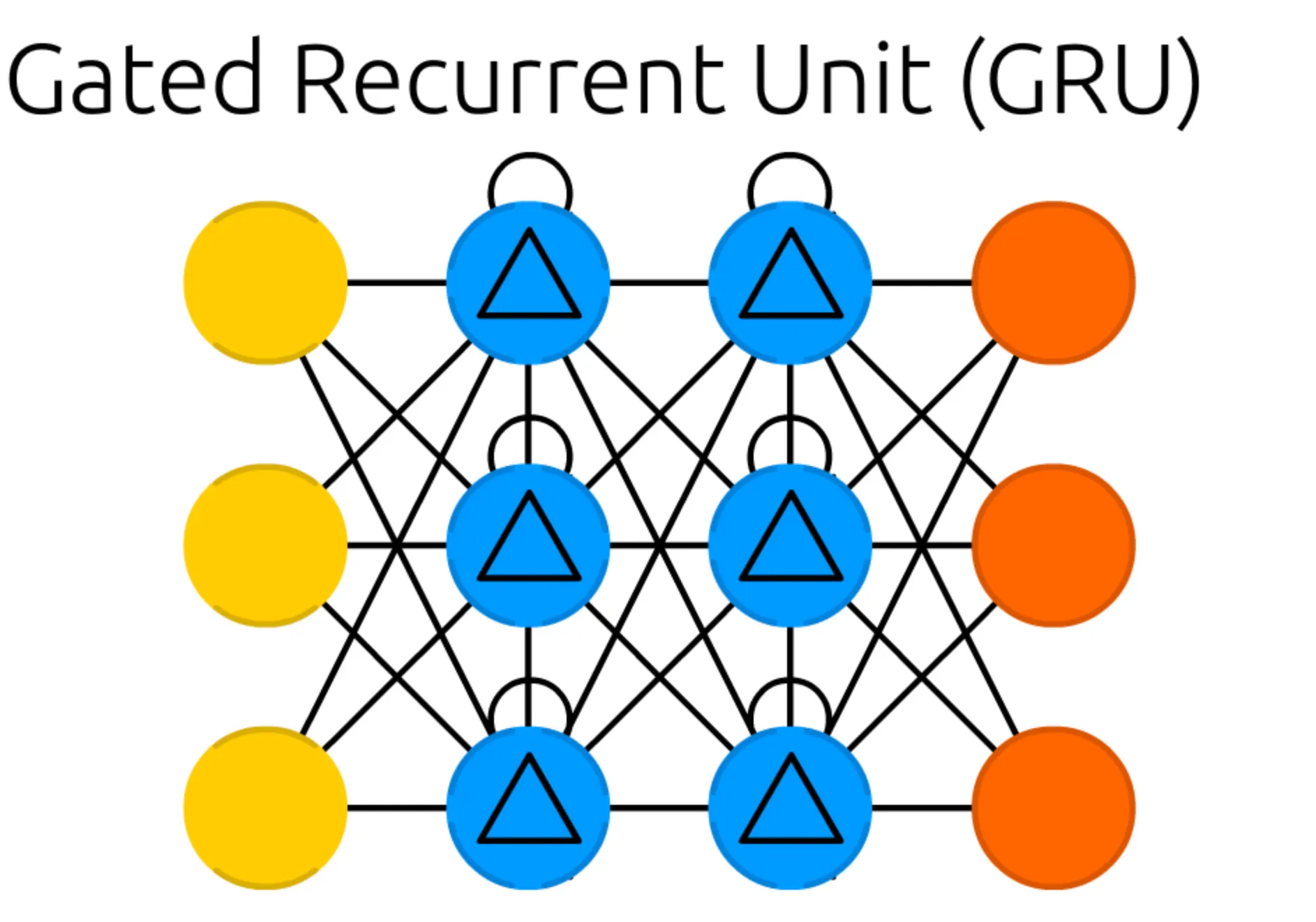
본 세션에서는, 이전 세션과 마찬가지로 RNN 을 기본으로 하여 설계된 ANN 이자, Recurrent Cell 이 존재하는 네트워크인 Gated Recurrent Unit (GRU) 에 대해서 알아보려고 합니다.
가장 먼저 보이는 구조의 특징적인 변화는 Recurrent Cell 이 있던 위치에, 내부에 정삼각형이 그려진 다른 Cell 이 존재한다는 점입니다. 이러한 형태의 Cell 을 Gated Memory Cell 이라고 합니다. 이전 RNN 이나 LSTM 때와 마찬가지로, Input Cell 과 Output Cell 및 Memory Cell 의 개수는 구조와 관련이 없다는 점 알아주시면 좋을 것 같습니다.
저번 시간에 보여드린 LSTM 은 Gradient Vanishing Problem 으로 인해 발생하는 학습 효과 저해 문제를 효과적으로 해결했다고 말씀드린 적 있습니다. 그렇다면, 이번에는 어떤 것이 문제가 되어 GRU 라는 새로운 네트워크를 구상하게 되었을까요?
결론부터 말씀드리자면, LSTM 에서 학습해야 할 parameter 가 꽤나 많았기 때문입니다. LSTM 에서 학습해야 할 요소들은 다음과 같았습니다.
1.
Forget Gate 의 계산에 필요한 xtx_t 와 곱해져야 하는 WxfW_{x_f}, ht−1h_{t-1} 와 곱해져야 하는 WhfW_{h_f}
2.
Input Gate 의 계산에 필요한 xtx_t 와 곱해져야 하는 WxiW_{x_i}, ht−1h_{t-1} 와 곱해져야 하는 WhiW_{h_i}
3.
Cell State 의 계산에 필요한 xtx_t 와 곱해져야 하는 WxCW_{x_C}, ht−1h_{t-1} 와 곱해져야 하는 WhCW_{h_C}
4.
Output Gate 의 계산에 필요한 xtx_t 와 곱해져야 하는 WxoW_{x_o}, ht−1h_{t-1} 와 곱해져야 하는 WhoW_{h_o}
5.
각 Gate 의 계산에 사용되는 bias 들
GRU 에서는 Output Gate 가 사라져 gate 의 총 개수가 줄어들었고, Cell State 의 개념이 사라져 구조를 기존의 LSTM 보다 간단하게 만들었기에 학습해야할 요소를 상대적으로 줄일 수 있었습니다.
그렇다면, 학습 요소를 줄인 GRU 의 구조는 어떠할까요?
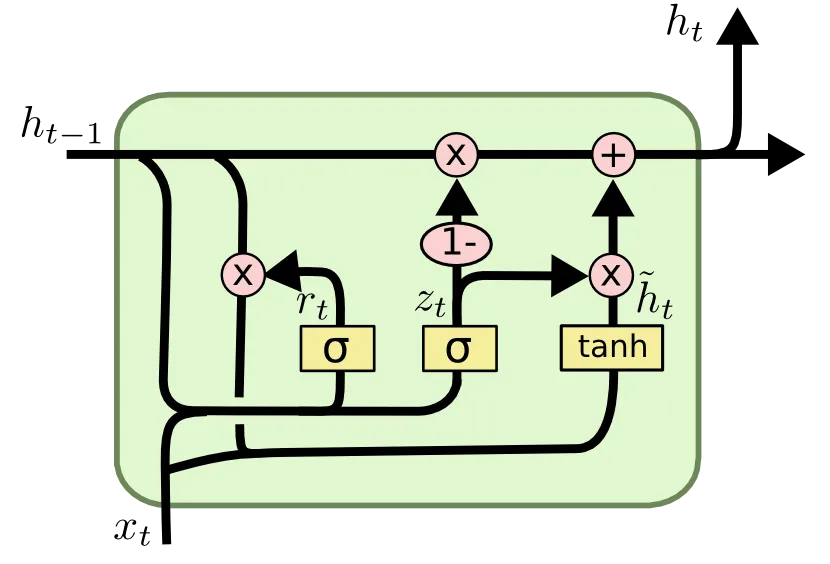
GRU 의 모습은 LSTM 과 굉장히 유사합니다만, 크게 다른 점은 두 가지 입니다.
1.
Forget Gate, Input Gate 가 존재했던 LSTM 과는 달리 GRU 에서는 Reset Gate 와 Update Gate 가 그 역할을 대신합니다.
2.
Cell State 가 사라졌습니다.
먼저, Reset Gate 에 대해서 설명을 드리려고 합니다.
위 사진의 rtr_t 로 명시된 값이 Reset Gate 입니다. 이는 "얼마나 이전 Cell 로 부터 넘어온 Hidden State 의 정보를 잊을 것인가" 에 대한 항목입니다.
rt=σ(Wxrxt+Whrht−1+br)r_t =\sigma(W_{x_r}x_t+W_{h_r}h_{t-1}+b_{r})
여기서 WxrW_{x_r} 와 WhrW_{h_r} 이 학습해야 할 요소이며, xtx_t 와 ht−1h_{t-1} 은 기존의 LSTM 에서도 소개드렸었던 tt 번째 timestamp 에서의 input 과 t−1t-1 번째 timestamp 에서 넘어온 hidden state 입니다.
다음으로, Update Gate 에 대해서 설명을 드리려고 합니다.
위 사진의 ztz_t 로 명시된 값이 Update Gate 입니다. 이는 "이전 timestamp 의 hidden state 와 현재 timestamp 의 Input 이 현재 hidden state 에 미치는 영향의 비율을 어떻게 설정할 것인가" 에 대한 항목입니다.
zt=σ(Wxzxt+Whzht−1+bz)z_t=\sigma(W_{x_z}x_t+W_{h_z}h_{t-1}+b_{z})
여기서도 마찬가지로 WxzW_{x_z} 와 WhzW_{h_z}이 학습해야 할 요소이며, xtx_t 와 ht−1h_{t-1} 은 기존의 LSTM 에서도 소개드렸었던 tt 번째 timestamp 에서의 input 과 t−1t-1 번째 timestamp 에서 넘어온 hidden state 입니다.
지금까지는 GRU 에 존재하는 두 가지 gate 에 대해서 알아보았습니다.
그렇다면 LSTM 에 비해서 바뀌게 될 hidden state 연산 과정은 어떻게 될까요?
GRU 에서는 Reset Gate 를 사용해 candidate hidden state 를 계산해내고, Update Gate 를 사용해 candidate hidden state 와 이전 timestamp 에서의 hidden state 의 비율을 조절하여 최종 Cell 의 Hidden State 를 계산하게 됩니다.
먼저, candidate hidden state 인 h~t\tilde{h}_t 는 다음과 같습니다.
h~t=tanh⁡(Wxhxt+Whhrt⊙ht−1+bh)\tilde{h}_t=\tanh(W_{x_h}x_t+W_{h_h}r_t\odot h_{t-1}+b_{h})
Sigmoid 에 의해 0~1 사이의 값을 가지는 Reset Gate 가 이전 timestamp 의 hidden state 에 곱해져 이 값을 바탕으로 candidate hidden state 를 형성하는 것을 볼 수 있습니다.
그리고, 이 Candidate Hidden State 를 사용해 Hidden State 를 연산하는 과정은 다음과 같습니다.
ht=zt⊙h~t+(1−zt)⊙ht−1h_t=z_t\odot\tilde{h}_t+(1-z_t)\odot h_{t-1}
마찬가지로, sigmoid 에 의해 0~1 사이의 값을 가지는 Update Gate 의 값에 따라 이전 timestamp 의 hidden state 와 현재 candidate hidden state 의 반영 비율이 결정되는 것을 볼 수 있습니다.
여기까지 오셨다면, GRU 의 구조에 대해서 모두 이해하신 것입니다. 다만, 아직 GRU 의 구조가 LSTM 에 비해서 학습할 parameter 가 적은지에 대해서 깊게 살펴보지 않았습니다. 지금부터는 같은 hidden state size nn 과 input size mm 을 가진다고 가정했을 때, 각 구조가 정량적으로 가지는 parameter 수에 대해서 알아보도록 합시다.
먼저, LSTM 에서 사용한 parameter 에 대해서 알아보도록 합시다. 앞에서 LSTM 에서 필요한 학습 parameter 를 정리한 적이 있습니다.
1.
Forget Gate 의 계산에 필요한 xtx_t 와 곱해져야 하는 WxfW_{x_f}, ht−1h_{t-1} 와 곱해져야 하는 WhfW_{h_f}
2.
Input Gate 의 계산에 필요한 xtx_t 와 곱해져야 하는 WxiW_{x_i}, ht−1h_{t-1} 와 곱해져야 하는 WhiW_{h_i}
3.
Cell State 의 계산에 필요한 xtx_t 와 곱해져야 하는 WxCW_{x_C}, ht−1h_{t-1} 와 곱해져야 하는 WhCW_{h_C}
4.
Output Gate 의 계산에 필요한 xtx_t 와 곱해져야 하는 WxoW_{x_o}, ht−1h_{t-1} 와 곱해져야 하는 WhoW_{h_o}
가정에서 각 gate 의 산출값은 n×1n\times 1 의 크기를 가져야 하기에, Wxf,Wxi,WxC,WxoW_{x_f}, W_{x_i}, W_{x_C}, W_{x_o} 는 n×mn\times m 의 크기를, Whf,Whi,WhC,WhoW_{h_f}, W_{h_i}, W_{h_C}, W_{h_o} 는 n×nn\times n 의 크기를, bias 항목이었던 bf,bi,bC,bob_{f}, b_{i}, b_{C}, b_{o} 는 n×1n\times 1 의 크기를 가지게 됩니다.
이를 바탕으로 LSTM 에서 필요한 parameter 의 개수를 다 더해보면 다음과 같습니다.
4(n2+mn+n)4(n^2+mn+n)
다음으로, GRU 에서 사용하는 학습할 parameter 를 정리해보면 다음과 같습니다.
1.
Reset Gate 의 계산에 필요한, xtx_t 와 곱해져야 하는 WxrW_{x_r}, ht−1h_{t-1} 와 곱해져야 하는 WhrW_{h_r}
2.
Update Gate 의 계산에 필요한, xtx_t 와 곱해져야 하는 WxzW_{x_z}, ht−1h_{t-1} 와 곱해져야 하는 WhzW_{h_z}
3.
Candidate hidden state 의 계산에 필요한, xtx_t 와 곱해져야 하는 WxhW_{x_h}, rt⊙ht−1r_t\odot h_{t-1} 와 곱해져야 하는 WhhW_{h_h}
확실히, numbering 만 해보아도 LSTM 보다 한 개의 항목이 줄어든 것을 볼 수 있습니다.
가정에서 각 gate 의 산출값은 n×1n\times 1 의 크기를 가져야 하기에, Wxr,Wxz,WxhW_{x_r}, W_{x_z}, W_{x_h} 는 n×mn\times m 의 크기를, Whr,Whz,WhhW_{h_r}, W_{h_z}, W_{h_h} 는 n×nn\times n 의 크기를, bias 항목이었던 br,bz,bhb_{r},b_{z},b_{h} 는 n×1n\times 1 의 크기를 가지게 됩니다.
이를 바탕으로 GRU 에서 필요한 parameter 의 개수를 다 더해보면 다음과 같습니다.
3(n2+mn+n)3(n^2+mn+n)
이렇게 이번 세션에서는 Long Short Term Memory (LSTM) 의 parameter 수를 줄인 네트워크인 Gated Recurrent Unit (GRU) 에 대해서 알아보는 시간을 가졌습니다. 실제로 GRU 가 LSTM 에 비해서 parameter 수를 줄이기는 했지만 가장 널리 쓰이는 Recurrent Neural Network 는 LSTM 이라고 합니다. 실제로 둘의 performance 자체도 크게 차이가 나지는 않습니다. GRU 는 LSTM 에 비해 적은 parameter 를 가져 적은 dataset 에서 더 유리하다고 알고 계시면 될 것 같습니다.