Duplicate

Lecture 16 | Image Mosaic

수강 일자
2022/11/01

Simple case: Translations

•
두 개의 parameter txt_x, tyt_y 를 구하는 것
•
Correspondence Point 를 찾은 이로부터 txt_x, tyt_y 를 구해내면 이미지를 matching 할 수 있음.
•
Mean Displacement of match
(1n∑i=1n(xi′−xi),1n∑i=1n(yi′−yi))=(tx,ty)(\frac{1}{n}\sum_{i=1}^n (x_i'-x_i), \frac{1}{n}\sum_{i=1}^n (y_i'-y_i)) = (t_x,t_y)
◦
Corresponding Point 간의 displacement 의 평균
•
하나의 Corresponding Point Pair 만 있어도 txt_x, tyt_y 는 구할 수 있음.
◦
Paramter 2 개, Corresponding Point Pair 하나마다 2 개의 equation 이 나오기 때문임.
◦
보통의 경우에는 unkown 의 수보다 equation 이 많은 overdetermined system 을 구성하고 Least Square Solution 을 사용함

Least Squares Formulation

•
Translation Transform
rxi=(xi+tx)−xi,      ryi=(yi+ty)−yi,r_{x_i}=(x_i+t_x)-x_i, \thickspace\thickspace\thickspace r_{y_i}=(y_i+t_y)-y_i,
◦
Squared Residual 의 합을 최소화하는 것을 목적으로 설정함
C(tx,ty)=∑i=1n(rxi2+ryi2)=∑i=1n((xi+tx−xi′)2+(yi+ty−yi′)2)\begin{align*} C(t_x,t_y) &= \sum_{i=1}^n (r_{x_i}^2 + r_{y_i}^2) \\ &= \sum_{i=1}^n ((x_i+t_x-x_i')^2 + (y_i+t_y-y_i')^2) \end{align*}
◦
위 식을 Matrix Formulation 으로 변경하여 구하면 다음과 같음.
▪
At=bAt=b 형태로 txt_x 와 tyt_y 가 가져야 하면 좋을 값을 bb 로 만든 형태임.
[10011001⋮⋮1001][txty]=[x1′−x1y1′−y1x2′−x2y2′−y2⋮xn′−xnyn′−yn]\begin{bmatrix} 1 & 0 \\ 0 & 1 \\ 1 & 0 \\ 0 & 1 \\ \vdots & \vdots \\ 1 & 0 \\ 0 & 1 \\ \end{bmatrix} \begin{bmatrix} t_x \\ t_y \end{bmatrix} = \begin{bmatrix} x_1'- x_1 \\ y_1' - y_1 \\ x_2'- x_2 \\ y_2' - y_2 \\ \vdots \\ x_n'- x_n \\ y_n' - y_n \\ \end{bmatrix}
▪
∥At−b∥2\| At-b\|^2 이 최소화되는 tt 를 찾는 것이 목표가 됨.
∥At−b∥2=(At−b)T(At−b)=bTb−tTATb−bTAt+tTATAt=bTb−2tTATb+tTATAt\begin{align*} \|At-b\|^2 &= (At-b)^T(At-b)\\ &= b^Tb -t^TA^Tb-b^TAt+t^TA^TAt \\ &= b^Tb-2t^TA^Tb+t^TA^TAt \\ \end{align*}
▪
미분해서 0 이 되도록 하는 값을 찾아봄
−2ATb+2ATAt=0ATAt=ATbt=(ATA)−1ATb-2A^Tb+2A^TAt = 0 \\ A^TAt = A^Tb \\ t = (A^TA)^{-1}A^Tb
▪
보통은 역행렬을 구하는데 O(n3)O(n^3) 의 시간복잡도가 필요하기에 위 식의 역행렬을 구하지 않고, 많은 프로그램들이 제공하는 Ax=bAx=b 의 solver 를 사용함.
•
Affine Transform
[x′y′1]=[abcdef001][xy1]\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} a & b & c\\ d & e & f \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}
◦
Residual & Cost Function 은 다음과 같음
rxi=(axi+byi+c)−xi′ryi=(dxi+eyi+f)−yi′C(a,b,c,d,e,f)=∑i=1n((rxi)2+(rxi)2)r_{x_i} = (ax_i + by_i +c)-x_i' \\ r_{y_i} = (dx_i + ey_i +f)-y_i' \\ C(a,b,c,d,e,f) = \sum_{i=1}^n ((r_{x_i})^2 + (r_{x_i})^2)
◦
Matrix Formulation 으로 변경하면 다음과 같음.
[x1y11000000x1y11x2y21000000x2y21⋮⋮⋮⋮⋮⋮xnyn1000000xnyn1][abcdef]=[x1′y1′x2′y2′⋮xn′yn′]\begin{bmatrix} x_1 & y_1 & 1 & 0 & 0 &0 \\ 0 & 0 & 0 & x_1 & y_1 &1 \\ x_2 & y_2 & 1 & 0 & 0 &0 \\ 0 & 0 & 0 & x_2 & y_2 &1 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ x_n & y_n & 1 & 0 & 0 &0 \\ 0 & 0 & 0 & x_n & y_n &1 \\ \end{bmatrix} \begin{bmatrix} a \\ b \\ c \\ d \\ e \\ f \end{bmatrix} = \begin{bmatrix} x_1'\\ y_1' \\ x_2'\\ y_2' \\ \vdots \\ x_n'\\ y_n'\\ \end{bmatrix}
•
Homography
[xi′yi′1]=[h00h01h02h10h11h12h20h21h22][xiyi1]\begin{bmatrix} x_i' \\ y_i' \\ 1 \end{bmatrix} = \begin{bmatrix} h_{00} & h_{01} & h_{02}\\ h_{10} & h_{11} & h_{12}\\ h_{20} & h_{21} & h_{22}\\ \end{bmatrix} \begin{bmatrix} x_i \\ y_i \\ 1 \end{bmatrix}
◦
Homogeneous Coordinate 에서의 표현이므로 각 xi′x_i', yi′y_i' 는 다음과 같음.
xi′=h00xi+h01yi+h02h20xi+h21yi+h22yi′=h10xi+h11yi+h12h20xi+h21yi+h22x_i' = \frac{ h_{00}x_i + h_{01}y_i + h_{02} }{h_{20}x_i + h_{21}y_i + h_{22}} \\ y_i' = \frac{ h_{10}x_i + h_{11}y_i + h_{12} }{h_{20}x_i + h_{21}y_i + h_{22}}
◦
Matrix Formulation 으로 변경하면 다음과 같음.
[xiyi1000−xi′xi−xi′yi−xi′000xiyi1−yi′xi−yi′yi−yi′][h00h01h02h10h11h12h20h21h22]=[00]\begin{bmatrix} x_i & y_i & 1 & 0 & 0 &0 & -x_i'x_i & -x_i'y_i & -x_i' \\ 0 & 0 &0 &x_i & y_i & 1 & -y_i'x_i & -y_i'y_i & -y_i' \\ \end{bmatrix} \begin{bmatrix} h_{00} \\ h_{01} \\ h_{02} \\ h_{10} \\ h_{11} \\ h_{12} \\ h_{20} \\ h_{21} \\ h_{22} \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}
▪
Homography 에서는 특이하게 min⁡∥At−0∥2\min \|At-0\|^2 의 문제를 풀게 됨.
▪
tt 는 up to scale 하므로 unit vector tt 에서만 문제를 해결하면 됨.
arg min⁡t∥At∥2  subject  to  ∥t∥2=1\argmin_t \|At \|^2 \thickspace \rm subject\thickspace to \thickspace\|t\|^2 =1
▪
8 unknowns → 4 개 이상의 Corresponding Points Pair 가 필요함.
▪
Solution: t^\hat t 는 ATAA^TA 의 smallest eigenvalue 를 가지는 eigenvector

Homography

arg min⁡tL(t)=∥At∥2=(At)T(At)=tTATAt  subject  to  tTt=1\argmin_t L(t)=\| At\|^2 = (At)^T(At) = t^TA^TAt \thickspace {\rm subject \thickspace to} \thickspace t^Tt=1
•
Lagrangian Multiplier λ\lambda 를 도입하여 다음과 같이 쓸 수 있음.
L(t)=tTATAt−λ(tTt−1)L(t)=t^TA^TAt - \lambda(t^Tt-1)
•
minimize 를 위해 tt 에 대한 derivative 이 0 인 tt 를 구함.
ATAt−λt=0A^TAt-\lambda t =0
◦
tt 는 λ\lambda 라는 eigenvalue 를 가지는 ATAA^TA 의 eigenvector
◦
∥At∥2=tTATAt=tTλt=λtTt=λ\|At\|^2 = t^TA^TAt = t^T\lambda t = \lambda t^Tt = \lambda 이기 때문에 ∥At∥2\|At\|^2 를 최소로 만드는 tt 는 least eigenvalue 를 가지는 eigenvector 이고, 그 때의 ∥At∥2\|At\|^2 값은 해당 eigenvalue 임. (Zero 일 수도 있음.)

Feature Matching

•
Mosaic 의 과정?
◦
Extract Interset Points (SIFT) → Unmatched Points 들로부터 matching 을 찾아냄 → Transformation 을 계산함
◦
많은 descriptor 사이의 match 를 찾는 과정이 Feature Matching
•
두 가지 방법론
◦
Exhaustive Search: 한 이미지의 feature 하나 당 다른 이미지의 모든 feature 를 순회하면서 비교해서 matching 되는 것들을 찾는, naive 한 방법론
◦
Nearest Neighbor Techniques: KD-tree 와 같은 tree 기반의 data structure 를 사용하면 neighereast neighbor 를 빠르게 찾을 수 있음.
•
Feature Matching 은 일반적으로 robust 하지 못하기 때문에 outlier 를 제거해내는 과정이 필요함.

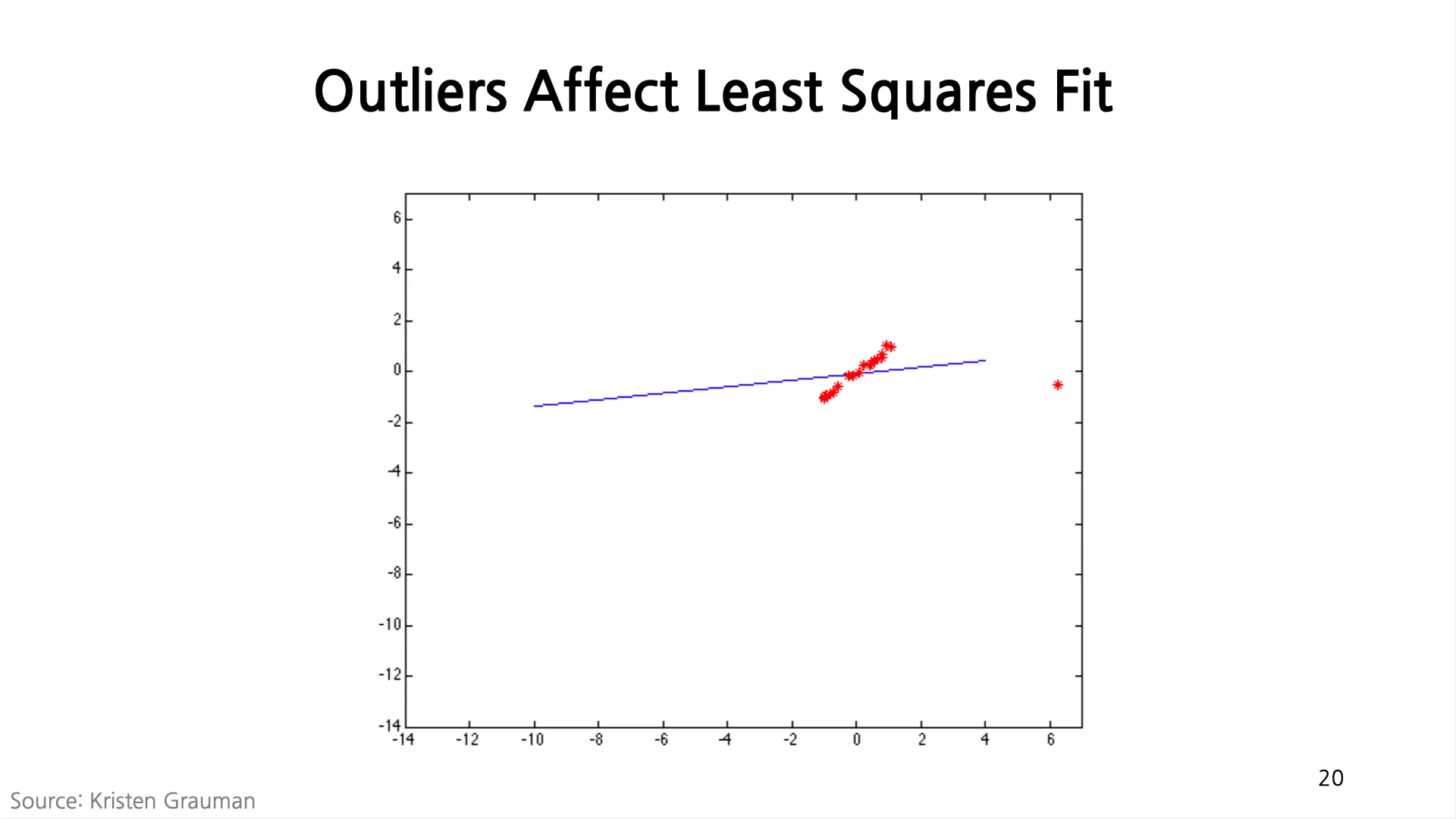
Outliers

•
Outlier 는 Homography 의 parameter 를 예측하는데 있어서 그 성능을 크게 떨어뜨림
•
Wrong Match 를 제거하고 Correct Match 만을 이용해 Homography 를 계산하는 것이 중요함

RANSAC (RANdom SAmple Consensus)

•
Approach: Outlier 의 영향을 피해 Inlier 들만 사용하여 모델을 fitting 하려는 접근
•
Intuition: Outlier 가 현재의 fitting 을 계산하는데 사용되었다고 하면, 결과로 나오는 fitting 이 나머지 데이터들로부터 support 를 받지 못할 것이라는 직관에 기반
•
RANSAC loop
1.
랜덤하게 seed group of points 를 선택함
2.
Seed group of points 를 이용해 transformation 을 예측함
3.
찾은 transformation 에 부합하는 inlier 들을 찾아냄 (fitting 과의 error 가 threshold 보다 작은 친구들의 집합을 inlier 로 정의함.)
4.1. 찾아낸 inlier 의 수가 충분히 많으면, 해당 inlier 들을 모두 이용해서 다시 transformation 을 계산함
4.2. 찾아낸 inlier 의 수가 충분히 많지 않으면 1 번으로 돌아감.

RANSAC Example: Translation

1.
하나의 Corresponding Point Pair 를 랜덤하게 선택함.
2.
선택한 Corresponding Point Pair 를 이용해 transformation 을 구함.
3.
한 이미지의 점에 transformation 을 거쳐서 나온 점과 그 점의 corresponding point 과의 차이가 threshold 보다 작으면 inlier 로 취급하고, 전체 inlier 의 개수를 셈.
4.1. Inlier 의 개수가 충분히 많으면 해당 inlier 들을 모두 이용해서 다시 transformation 을 계산함.
4.2. Inlier 의 개수가 충분히 많지 않으면 1 번으로 돌아감.

RANSAC Pros and Cons

•
Pros
◦
Simple and General
◦
다양한 fitting 문제에 적용할 수 있음.
◦
현실에서도 잘 동작함.
•
Cons
◦
Seed Group 의 개수, Inlier 를 결정하기 위한 threshold, Inlier 가 충분히 많은지를 판단하기 위한 threshold 등 tuning 해야할 parameter 가 많음.
◦
Inlier ratio 가 낮으면 잘 동작하지 않음. (ex. 100 개의 matching 중 10 개만 실제로 correct matching 인 경우) → Keypoint Extraction 이나 Descriptor 를 바꾸는 것이 졸을 수도 있음.
◦
최소한의 개수를 이용해 transformation 을 초기에 구하는 것이 항상 좋은 initialization 이라고 보장할 수 없음.

Image Warping

•
RANSAC 으로 transformation 을 구했을 때, 해당 transformation 을 적용하여 변형한 이미지는 어떻게 변할 것인가를 알아내는 과정
g(x′,y′)=f(T(x,y))g(x', y') = f(T(x,y))
•
Foward Warping, Inverse Warping 이 있는데, Inverse Warping 이 더 활용하기가 좋음.
•
Forward Warping
◦
원본 이미지로부터 시작해서 두 번째 이미지를 만들어내는 과정
◦
f(x,y)f(x,y) 에 존재하는 픽셀 값을 대응되는 위치인 (x′,y′)=T(x,y)(x',y')= T(x,y) 로 보내면 됨.
◦
하지만, 변환된 (x′,y′)(x',y') 가 일반적으로 특정 픽셀에 딱 떨어지지 않음. → Splatting (x′,y′)(x',y') 근처의 픽셀에 색상을 배분해주는 과정을 활용함.
•
Inverse Warping
◦
변환된 두 번째 이미지로부터 원본 이미지를 재구성하려는 과정에서 나타나는 관계를 바탕으로 두 번째 이미지의 값들을 알아내는 과정
◦
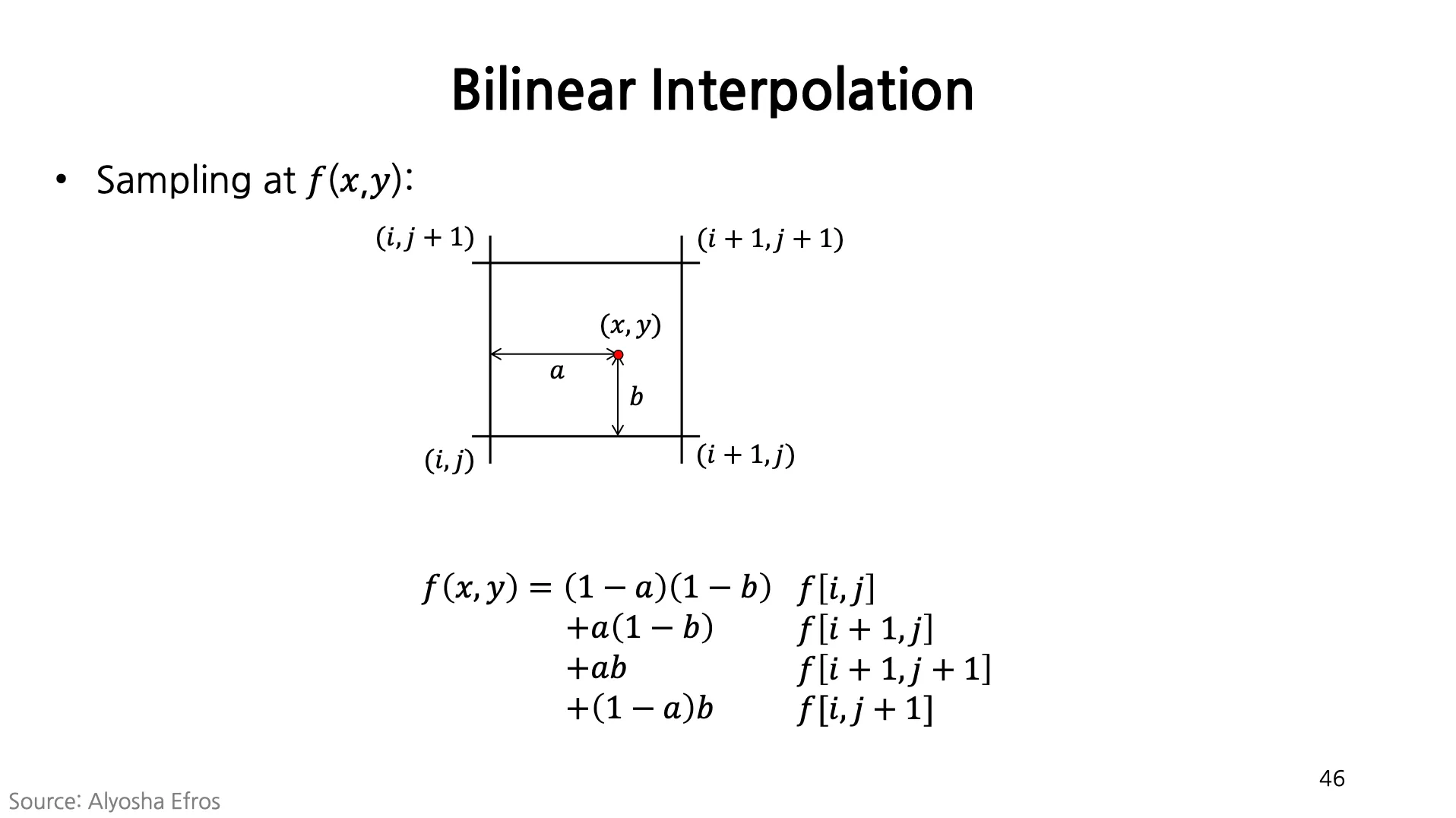
g(x′,y′)g(x',y') 의 각 픽셀에 T−1(x′,y′)T^{-1}(x',y') 를 적용하여 구해낸 원본 이미지의 위치의 픽셀값을 interpolation 으로 구해낼 수 있음. (값을 splatting 하는 것은 어렵지만 아는 값을 interpolation 하는 것은 쉬움.)

Bilinear Interpolation

f(x,y)=(1−a)(1−b)f[i,j]+a(1−b)f[i+1,j]+abf[i+1,j+1]+(1−a)bf[i,j+1]\begin{align*} f(x,y) &= (1-a)(1-b) &f[i,j] \\ &+ a(1-b) &f[i+1,j] \\ &+ ab &f[i+1,j+1] \\ &+ (1-a)b &f[i,j+1] \\ \end{align*}

Image Warping with Homographies

•
우측 그림의 검은색 영역은 Inverse Transformation 을 적용했을 때 원본 이미지의 범위 밖으로 나가서 표현될 수 없는 지역임.

Image Rectificaiton

•
원하는 네 개의 지점이 변환된 이미지에서 원하는 네 개의 지점 (위 그림에서는 recangle 형태를 이루도록) 으로 이동하길 원한다- 를 정하면, 이를 통해 transformation (homography) 을 구할 수 있고 변환할 수 있음.

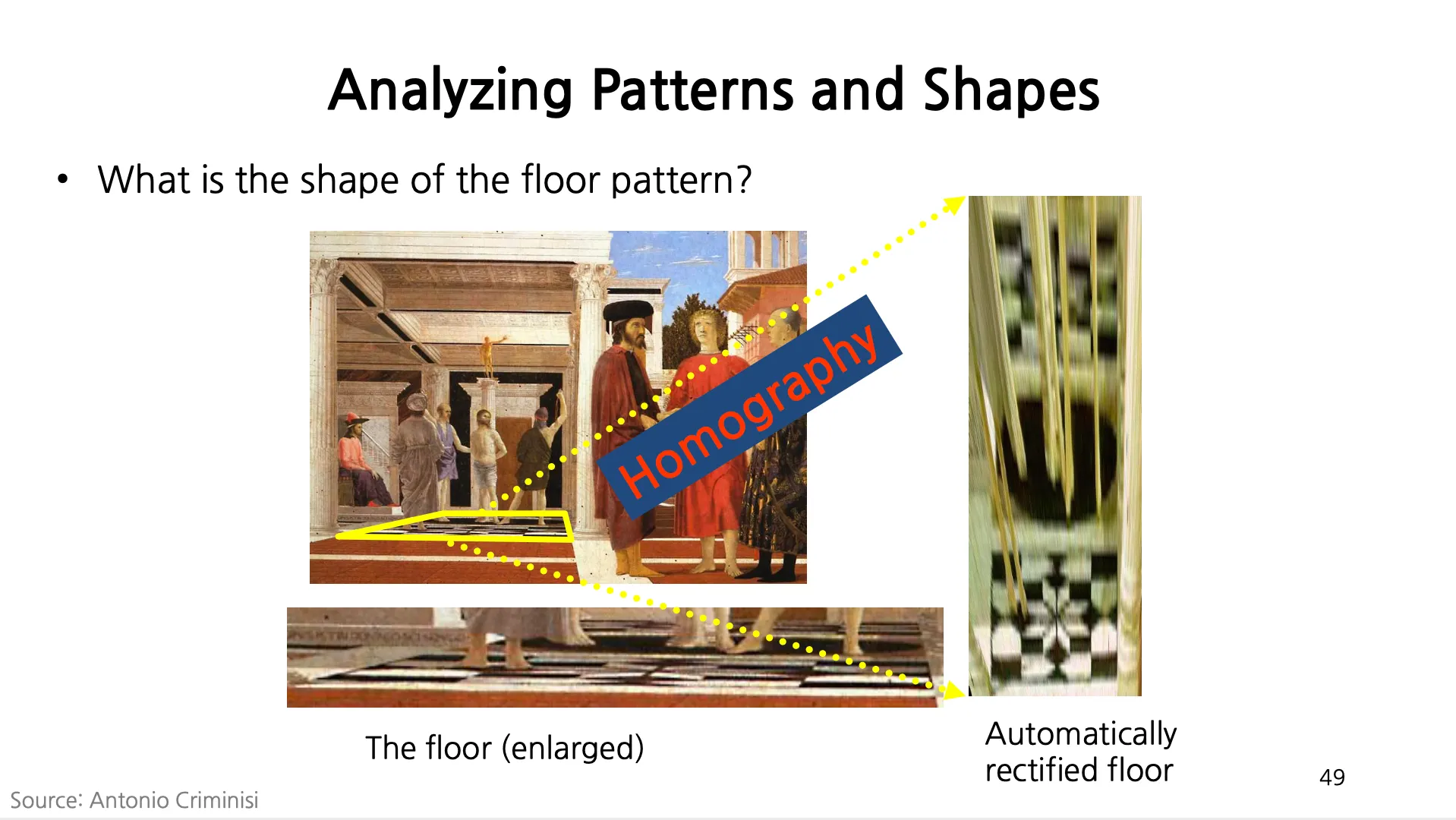
Analyzing Patterns and Shapes + Application

•
이미 알고 있는 (유명한 성당의 바닥 등) 정보를 추가적으로 이용하여 하나의 이미지만으로도 원하는 뷰의 모습을 얻어낼 수도 있음.
•
항공사진의 연속적, 불균형한 사진들을 이용해 파노라마를 만들 수 있음.

Summary: Alignment & Warping

•
2D transformations
◦
2D Matrix 형태로 표현할 수 있는 translation 과 같은 transformation 들이 존재
•
Fitting transformations
◦
두 이미지에서 선택한 Corresponding Point Pairs 를 이용해 unkown parameter 를 구하는 과정 (Affine, Homography) 를 다룸
◦
Outlier 를 제거하고 inlier 를 선택하는 RANSAC
•
Perform Image Warping
•
Mosaics
◦
동일한 center of projection 에서 찍힌 여러 장의 이미지를 Homography 와 Image Warping 을 통해서 merge 하는 과정