Duplicate

CV_HW2

마감일
2022/10/19
제출자
전기정보공학부 2017-12433 김현우

1. Edge Detection

1.
[5] Why is the Laplacian alone not a good edge detector, but the Laplacian of Gaussian is? Explain in a sentence each.
Since Laplacian is too sensitive against the noise, even non-edge parts of the image can be detected to be edge using the Laplacian as a edge detector. However, Laplacian of Gaussain first smooth the noise using Gaussian, which makes Laplacian could work well on detecting edge compared to Laplacian alone.
2.
[5] What is the general effect of increasing the Gaussian width for Laplacian of Gaussian edge detectors? Explain in a sentence.
Larger width Laplacian of Gaussian edge detectors generally deal with large area of the image region, therefore the detection ability on local region will be reduced but the noise sensitivity can be also reduced, too.

2. Hough Transform Line Parameterization

1.
[5] Show that if you use the polar representation for lines ρ=xcos⁡θ+ysin⁡θ\rho = x\cos\theta + y\sin\theta, each point (x,y)(x,y) in the xy-plane results in a sinusoid in the (ρ,θ)(\rho, \theta) plane. Show the amplitude and phase of the sinusoid in terms of the point (x,y)(x,y).
We can change the parameteric polar representation as below.
ρ=xcos⁡θ+ysin⁡θ=x2+y2(xx2+y2cos⁡θ+yx2+y2sin⁡θ)\begin{align*} \rho &= x\cos\theta + y\sin\theta \\ &=\sqrt{x^2+y^2}(\frac{x}{\sqrt{x^2+y^2}}\cos\theta + \frac{y}{\sqrt{x^2+y^2}}\sin\theta) \\ \end{align*}
Then, we can consider ϕ\phi such that sin⁡ϕ=xx2+y2\sin\phi = \frac{x}{\sqrt{x^2+y^2}} and cos⁡ϕ=yx2+y2\cos\phi=\frac{y}{\sqrt{x^2+y^2}}. Then, the equation can be simplified as velow.
ρ=xcos⁡θ+ysin⁡θ=x2+y2(xx2+y2cos⁡θ+yx2+y2sin⁡θ)=x2+y2(sin⁡ϕcos⁡θ+cos⁡ϕsin⁡θ)=x2+y2sin⁡(θ+ϕ)\begin{align*} \rho &= x\cos\theta + y\sin\theta \\ &=\sqrt{x^2+y^2}(\frac{x}{\sqrt{x^2+y^2}}\cos\theta + \frac{y}{\sqrt{x^2+y^2}}\sin\theta) \\ &=\sqrt{x^2+y^2}(\sin\phi\cos\theta+ \cos\phi\sin\theta) \\ &=\sqrt{x^2+y^2}\sin(\theta+\phi) \\ \end{align*}
The above equation is the form of sinusoid wave form which has the amplitude of x2+y2\sqrt{x^2+y^2} and phase of ϕ\phi. Since we set ϕ\phi to be sin⁡ϕ=xx2+y2\sin\phi = \frac{x}{\sqrt{x^2+y^2}} and cos⁡ϕ=yx2+y2\cos\phi=\frac{y}{\sqrt{x^2+y^2}}, ϕ\phi can be expressed as ϕ=arctan⁡(xy)\phi=\arctan(\frac{x}{y}).
Thus, the amplitude is x2+y2\sqrt{x^2+y^2} and phase is arctan⁡(xy)\arctan(\frac{x}{y}).
2.
[5] Assuming that the image points (x,y)(x,y) are in a image of width WW and heigh HH, what is the maximum absolute value of ρ\rho and the range for θ\theta?
Maximum absolute value of the sinusoidal form of the specific point (x,y)(x,y) is the amplitude of the equation, which is x2+y2\sqrt{x^2+y^2} and the period of the sinusoidal form is 2π2\pi.
Since the image size is W×HW\times H, we can say that the maximum absolute value of ρ\rho is W2+H2\sqrt{W^2+H^2}. Also, we can simply take one period of range such as [0,2π)[0, 2\pi) for θ\theta.

3. Active Contours

Imagine you are trying to implement active contours, or the ’snakes’ method for finding shapes.
1.
[4] You finish implementing the external energy term, but forget to implement the internal energy term. What kinds of issues may arise with your snakes? Explain in a sentence.
If we forget to implement the the internal energy term, we cannot apply smoothness or elasticity on contours, causes the contours to be too sensitive to noise (detect edge even if is not) and also we cannot apply prior knowledge on contours.
2.
[3] You realize your mistake, and implement the internal energy term, as well. However, you notice that your snakes are too rounded, and are not fitting the shapes well. How can you address this problem? Explain in a sentence.
External energy term deals with the exact fitting of the shape, thus we can increase the weight parameter of external energy compared to internal energy term.
3.
[3] You notice that in your images, the shape you want to fit to is always a rectangle. How can you encourage your snakes to fit to rectangular shapes? Explain in a sentence.
If we know the prior knowledge of the shape, we can add the inernal energy term which can penalize the large difference between prior knowledge and obtained contour (e.g., adding the squared error term of point distance between four vertices of rectangle).

4. Apperanance and BRDFs

Consider a hypothetical material with a BRDF given by ρ(θi,θr)=1cos⁡(θi)\rho(\theta_i,\theta_r)=1\cos(\theta_i), where θi\theta_i is the angle made by the light direction with the surface normal, and θr\theta_r is the angle made by the viewing direction with the surface normal.
1.
[5] Will the appearance of this surface vary with the viewing direction? Explain why.
If we assume the light source is fixed, radiance intensity II keep constant. Since the surface radiance as ρ(θi,θr)Icos⁡θi\rho(\theta_i,\theta_r)I\cos\theta_i, we can calculate the surface radiance is Icos⁡2θiI\cos^2\theta_i which is independent of viewing direction. Thus the appearance of the surface will not vary with the viewing direction.
2.
[5] Will it vary with the incoming light direction? Explain why. As we calulated the surface radiance as Icos⁡2θiI\cos^2\theta_i in above question 4-(1), we can say that the surface radiance is proportional to the square cosine of incoming light direction. Also we can assume the fixed light source which means the radiance intensity II keep constant in this case, the appearance of the surface will vary with the incoming light direction

5. Implementing the Hough Transform for Line Detection

2.
Non Maximal Suppression Algorithm in Edge Detection
For each pixel, we retrieves the two nearest neighbor pixel which are aligned in gradient direction and compare the gradient magnitude. We only keep the gradient value of the pixel when it is greater than the two neighborhood pixels. Otherwise we initialize the gradient value as 0.
Since the gradient direction can be expressed as the positive angle to the xx-axis and each pixel have 8 neighborhoods, we can think of equally dividing 360°360\degreeto 8 regions as below.
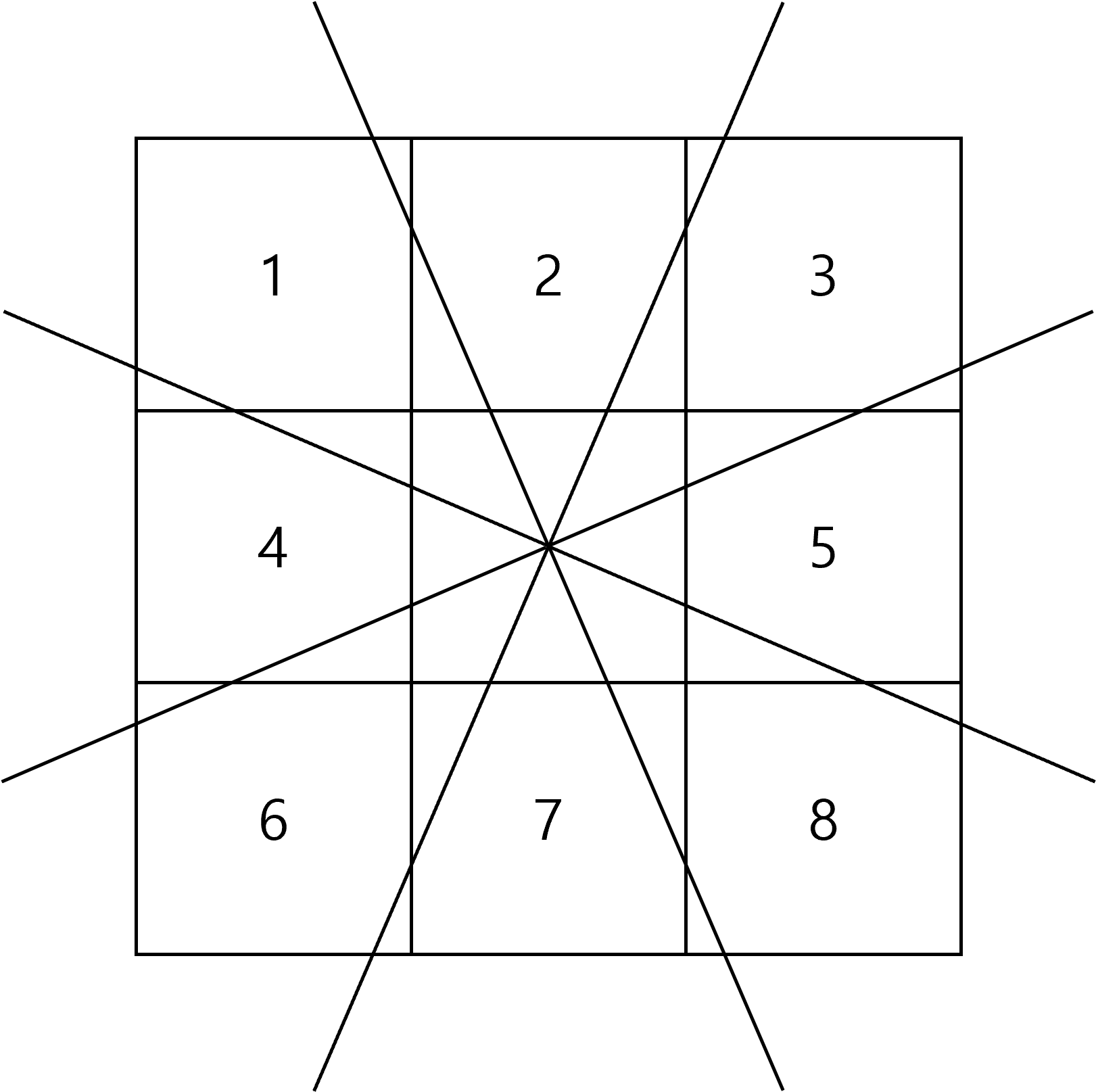
Region Division
Each region are covering 45°45\degree area. For example using above figure, if the gradient direction ϕ\phi satisfies ϕ∈[−22.5°,22.5°)\phi \in[-22.5\degree, 22.5\degree), we need to compare magnitude value of center pixel to pixel 4 and pixel 5. If the center pixel has greater graident magnitude than both pixel 4’s and pixel 5’s one, we keep the gradient value. Otherwise we initialize the center pixel’s gradient magnitude value as 0, explicitly setting it is not the edge region.
3.
(1) Grayscale Image of ImI_m, HH
name
ImI_m
HH
Img01
Img02
Img03
Img04
3.
(2) Parameters used in this question
4.
(1) Non Maximal Suppression Algorithm in Hough Line Detection
I used Non Maximal Suppresion Algorithm implemented in below link (function named find_local_maxima).
The main idea of the function is remaining the voted value only when it is the most greatest value among the specific size of the neighbors (in the code they use 3×33\times 3, but I treated them as parameters to calibrate). Else, the voted value are initialized with 0.
computer-vision-algorithms/hough.py at master · aleju/computer-vision-algorithms
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters You can't perform that action at this time. You signed in with another tab or window.
https://github.com/aleju/computer-vision-algorithms/blob/master/computer-vision/hough.py
4.
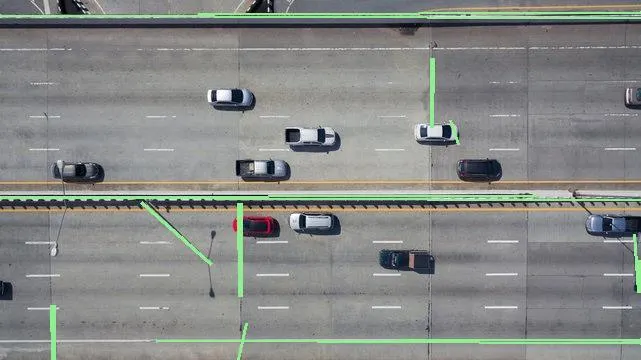
(2) Line Plotting on Images
Image 1 - Line Plotting
Image 2 - Line Plotting
Image 3 - Line Plotting
Image 4 - Line Plotting
4.
(3) Reason why rρr_\rho, rθr_\theta is needed
We need rρr_\rho, rθr_\theta is because we need to change the index of Hough Accumulator to real ρ\rho and θ\theta and find out lines on Image Space.
5.
Line Segment Plotting on Images
Image 1 - Line Segment Plotting
Image 2 - Line Segment Plotting
Image 3 - Line Segment Plotting
Image 4 - Line Segment Plotting