Duplicate

Lecture 4 | Projective Transformations

수강 일자
2023/02/23

2D Projective Transformations

•
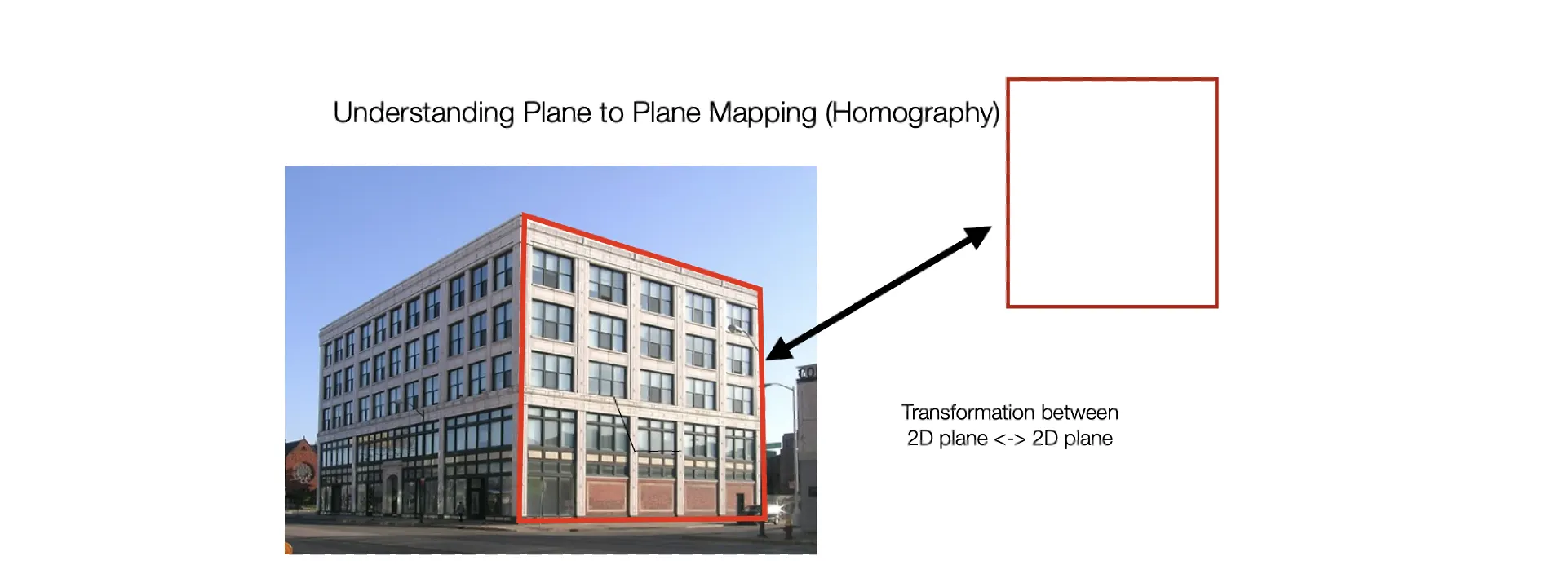
실제 세상에서는 직사각형인 것이 이미지 상에서는 그렇게 보이지 않음.
•
실제 세상에서 AA 로 보이는 것이 이미지 상에서는 BB 로 보이는 경우가 종종 있음.

2D Projective Geometry

•
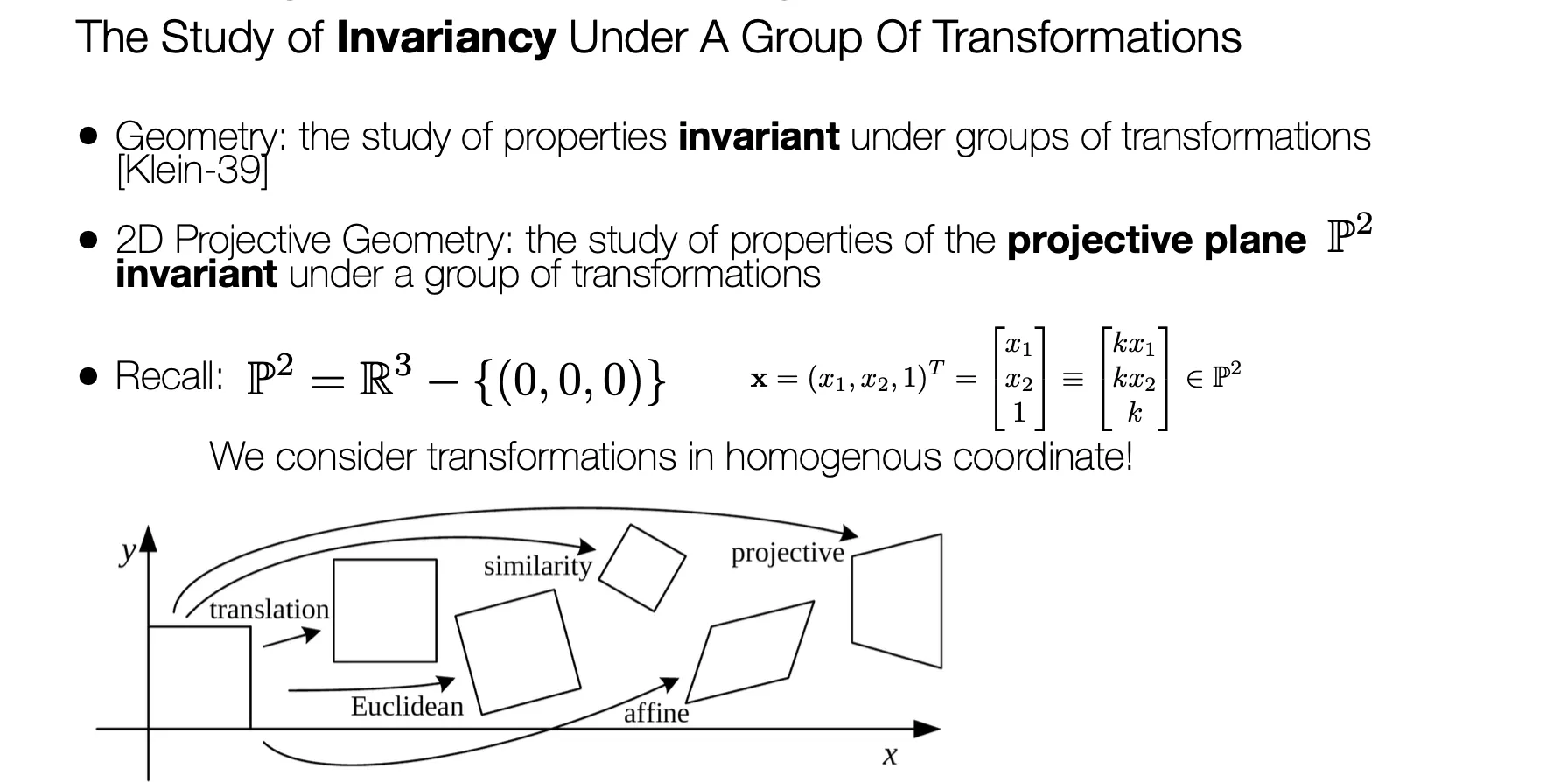
Geometry 는 Transformation 에서 유지되는 invariants 에 대한 연구임.
•
2D Projective Geometry 는 한 Projective Plane P2\mathbb P^2 에서 다른 Projective Plane P2\mathbb P^2 으로의 변환에서 유지되는 invariants 에 대한 연구임.

Homograph (Projectivity)

•
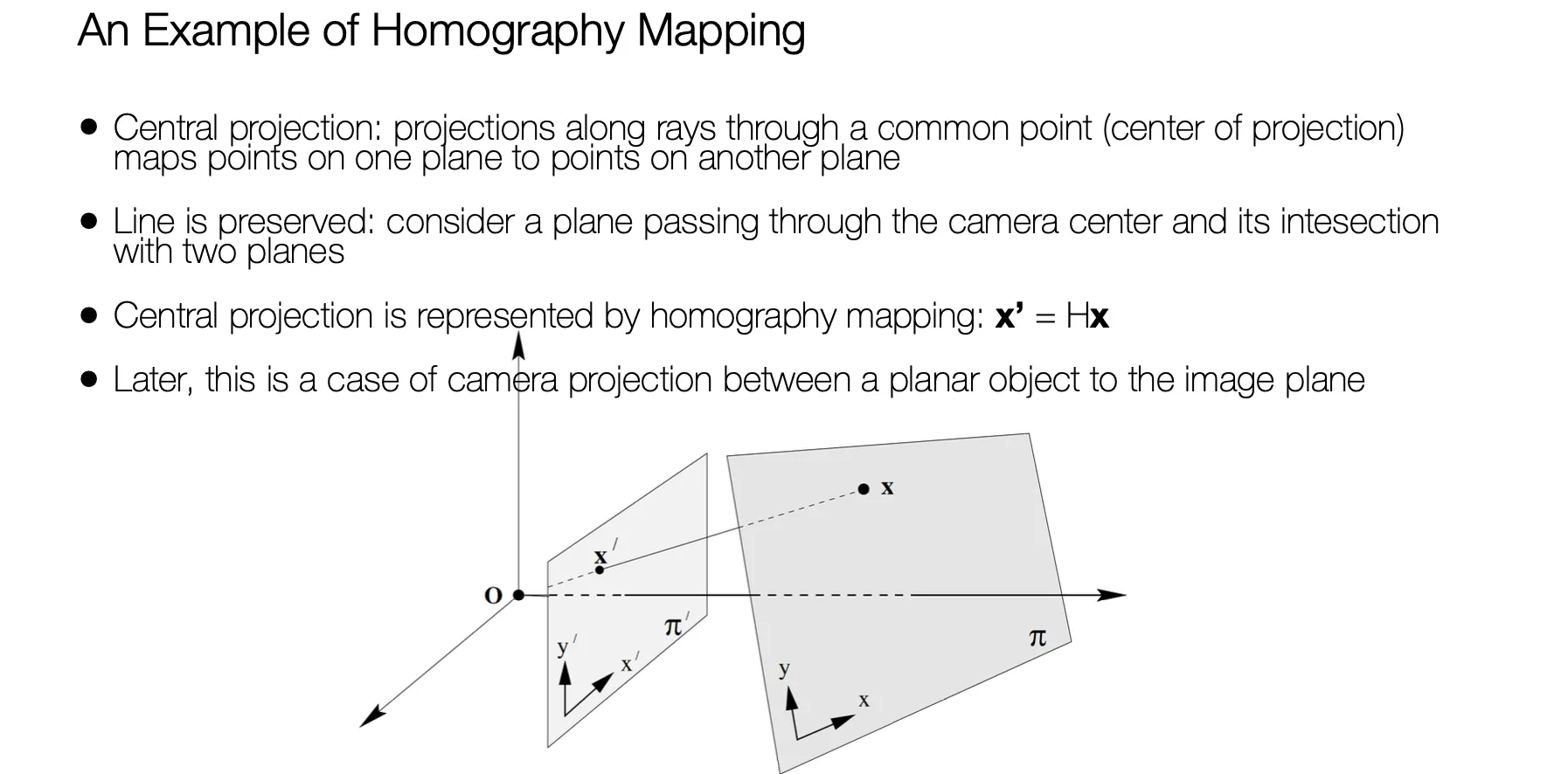
P2\mathbb P^2 에서 P2\mathbb P^2 로의 Invertible Mapping
•
Projectivity == Colineation == Projective Transform == Homography
•
Homography 의 가장 중요한 특성은 Plane-to-Plane Mapping 임.
◦
직선은 다른 Projective Plane 에서도 직선으로 표현됨.
•
Example of Non-Homography Transformation
◦
Radial Lens Distorsion 과 같은 현상들이 Non-Homography 임.

Homograph (Projectivity)

(x1′x2′x3′)=[h11h12h13h21h22h23h31h32h33](x1x2x3)→x′=Hx\begin{pmatrix} x_1' \\ x_2' \\ x_3' \end{pmatrix}= \begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \\ \end{bmatrix} \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} \\ \quad \\ \to {\rm x'} = {\rm H}{\rm x}
•
3×33\times3 Non-Singular Matrix 는 모두 Homography 임.
◦
Colinearity 를 보여줌으로써 증명할 수 있음.
(H−Tl)T(Hxi)=(lTH−1)(Hxi)=0({\rm H}^{-T}{\rm l})^T({\rm H}{\rm x}_i) = ({\rm l}^T{\rm H}^{-1})({\rm H}{\rm x}_i) = 0
▪
밑에서 나오지만 line mapping 은 l′=H−Tl{\rm l'} = {\rm H}^{-T}{\rm l} 를 활용함.
•
Homography 는 모두 3×33\times3 Non-Singular Matrix 로 표현할 수 있음.
•
Homography 는 Up-to-Scale 임. (좌표 자체가 Homogeneous Coordinate 이므로!)
◦
9DoF - 1DoF (Up-to-Scale) = 8DoF

Homograph (Projectivity)

x′=Hxl′=H−Tl{\rm x'} = {\rm H}{\rm x} \quad {\rm l'} = {\rm H}^{-T}{\rm l}
•
점에 대한 변환이 H\rm H 이면, 동일한 변환은 선에 대해서는 H−T{\rm {H}}^{-T} 로 표현할 수 있음.
•
증명은 다음과 같음. (Line Form 식이 동일하면 값도 동일하다는 가정 필요)
l′Tx′=l′THx=(HTl′)Tx=0lTx=0→l′=H−Tl{\rm l'}^T{\rm x'} = {\rm l'^T}{\rm H}{\rm x} = ({\rm H}^{T}{\rm l'})^T{\rm x} = 0 \\ {\rm l}^T{\rm x} = 0 \\ \to {\rm l'} = {\rm H}^{-T}{\rm l}

Homograph (Projectivity)

x′=HxC′=H−TCH−1{\rm x'} = {\rm H}{\rm x} \quad C' = {\rm H}^{-T}C{\rm H}^{-1}
•
점에 대한 변환이 H\rm H 이면 Conic 에 대한 변환은 H−TCH−1{\rm H}^{-T}C{\rm H}^{-1} 로 표현할 수 있음.
•
증명은 다음과 같음. (Conic Form 식이 동일하면 값도 동일하다는 가정 필요)
x′TC′x′=(Hx)TC′(Hx)=xT(HTC′H)x=0xTCx=0→C′=H−TCH−1{\rm x'}^TC'{\rm x'} = ({\rm H}{\rm x})^TC'({\rm H}{\rm x}) = {\rm x}^T({\rm H}^TC'{\rm H}){\rm x = 0} \\ {\rm x}^TC{\rm x} = 0 \\ \to C' = {\rm H}^{-T}C{\rm H}^{-1}

More Examples using Homography

•
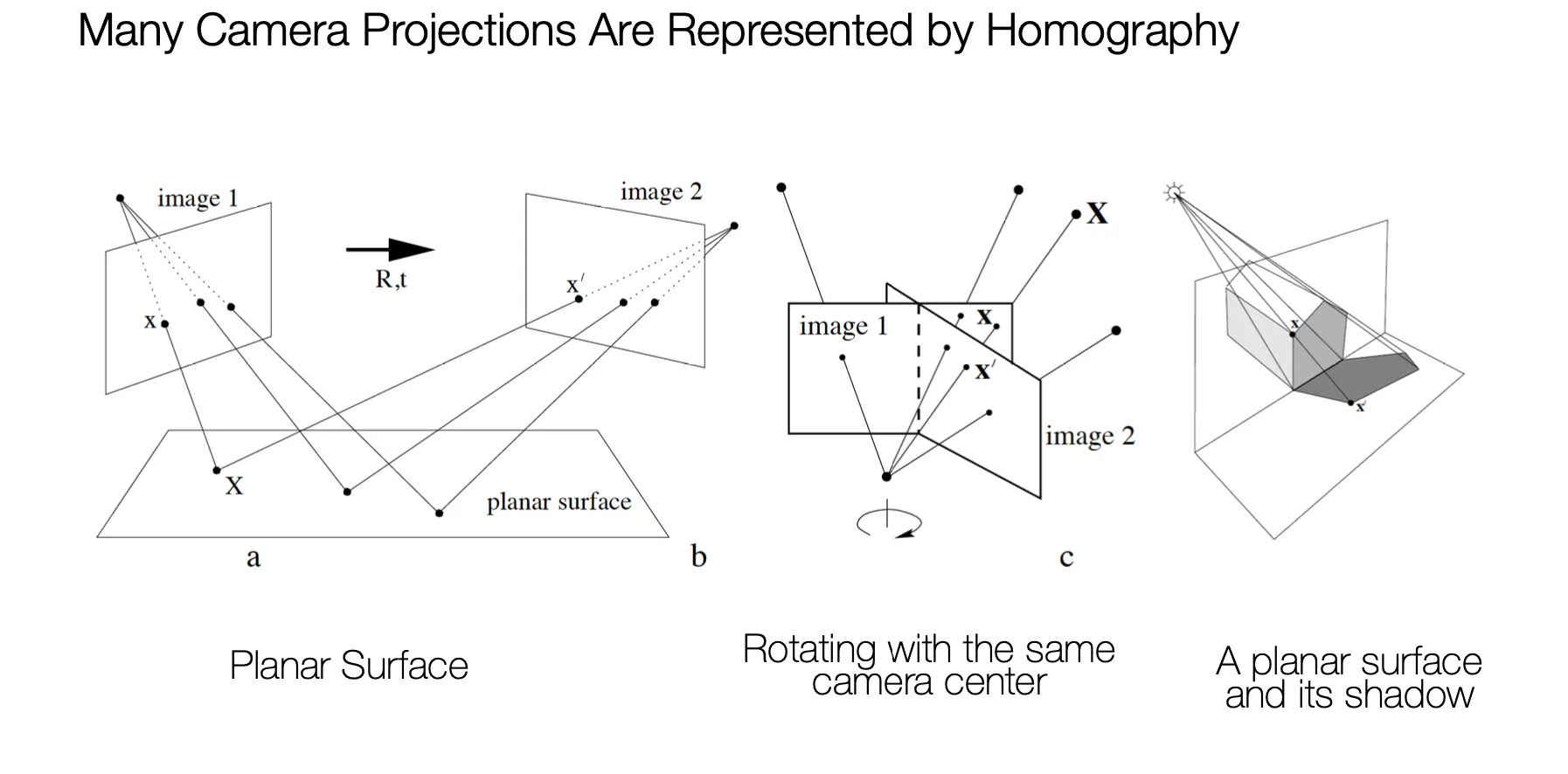
Central Projection
◦
카메라 위치는 고정하고 view direction 과 focal length 만 달리 할 경우도 Homography 로 나타낼 수 있음.
•
Planar Surface
◦
Planar Surface 에 한 번 상이 반사되고 다시 다른 Image Plane 에 맺혔을 때의 결과도 Homography 로 나타낼 수 있음.
•
Rotating Camera
◦
카메라의 위치 및 focal length 를 고정하고 direction 만 회전시킨 경우도 Homography 로 나타낼 수 있음.
•
Planar Surface and Shadow
◦
그림자까지 Homography 로 나타낼 수 있음.

A Hieararchy of Transformations: Transformation

x′=x+t↔x′=[I2×2t02×11]x→[x1+t1x2+t21]=[I2×2t02×21][x1x21]{\rm x'} = {\rm x} + {\rm t} \quad \lrarr \quad {\rm x'} = \begin{bmatrix} {\rm I}_{2\times 2} & {\rm t} \\ {\rm 0}_{2\times 1} & 1 \end{bmatrix}{\rm x} \\ \quad \\ \to \begin{bmatrix} x_1 + t_1 \\ x_2 + t_2 \\ 1 \end{bmatrix} = \begin{bmatrix} {\rm I}_{2\times 2} & {\rm t} \\ {\rm 0}_{2\times 2} & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2\\ 1 \end{bmatrix}
•
좌측: Inhomogeneous Coordinate, 우측: Homogeneous Coordinate
•
Homogeneous Coordinate 은 Matrix Multiplication 이므로 연속적인 변환이나 역변환을 하기에 용이함.
•
2DoF for t{\rm t}

A Hieararchy of Transformations: Euclidean Transform (Translation + Rotation)

x′=Rx+t↔x′=[R2×2t02×11]x{\rm x'} = R{\rm x} + {\rm t} \quad \lrarr \quad {\rm x'} = \begin{bmatrix} {\rm R}_{2\times 2} & {\rm t} \\ {\rm 0}_{2\times 1} & 1 \end{bmatrix}{\rm x} \\
•
좌측: Inhomogeneous Coordinate, 우측: Homogeneous Coordinate
•
R\rm R 은 다음과 같이 표현됨.
R=[cos⁡θ−sin⁡θsin⁡θcos⁡θ]{\rm R} = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}
◦
R\rm R 자체는 1DoF (변수는 θ\theta 하나 뿐임)
◦
Rotation Matrix 가 되려면 1. Orthonormal + 2. det(R)=1det(\rm R) = 1 의 두 조건을 만족해야 함.
▪
이 두 조건을 만족하는 것들을 Special Orthogonal Group, SO(N) 이라고 부름.
▪
3D Vision 에서 자주 등장하는 Rotation Matrix 는 3DoF 인 R∈SO(3){\rm R} \in SO(3) 임.
•
길이, 각도, 넓이, 순서 (reflection 이 없기 때문에 유지되는 term) 이 유지됨.
•
3DoF: 1DoF for t{\rm t} + 2DoF for R{\rm R}
•
두 Euclidean Transformation 의 연속적인 변환은 하나의 Euclidean Transformation 으로 나타낼 수 있음. → Matrix Multiplication 해보면 같은 형태가 등장함으로 증명할 수 있음!

Rotation and Translation

•
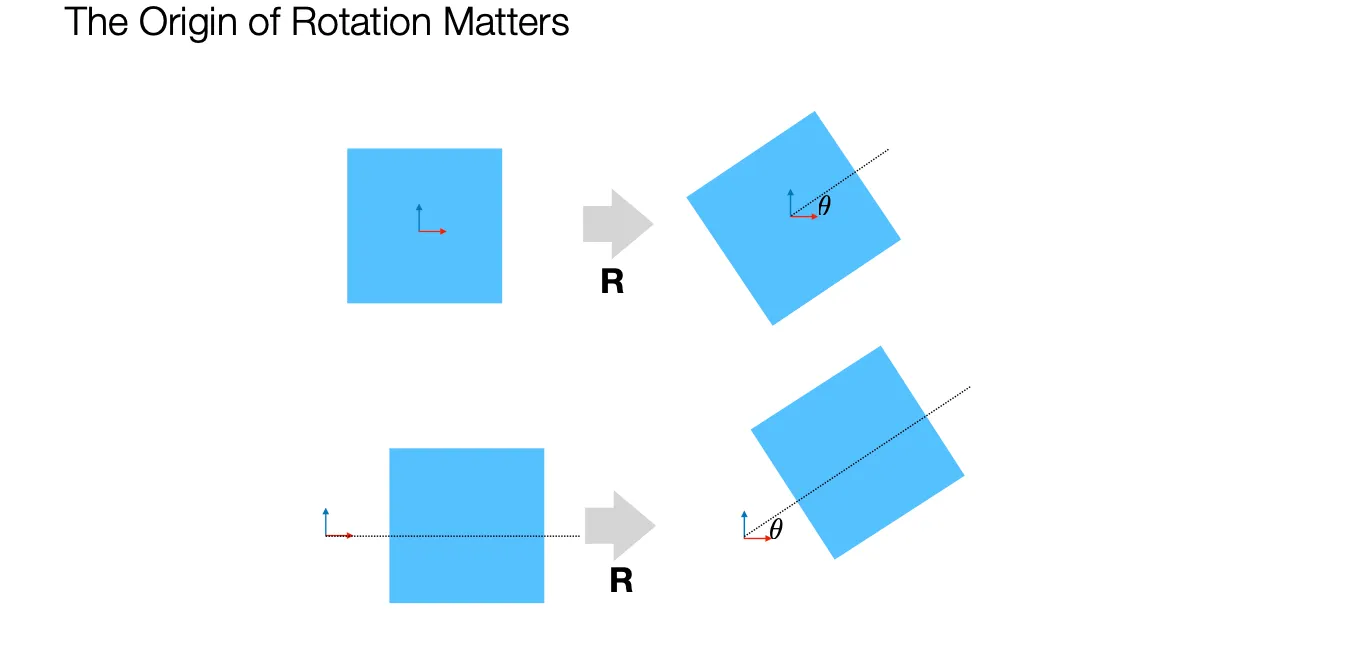
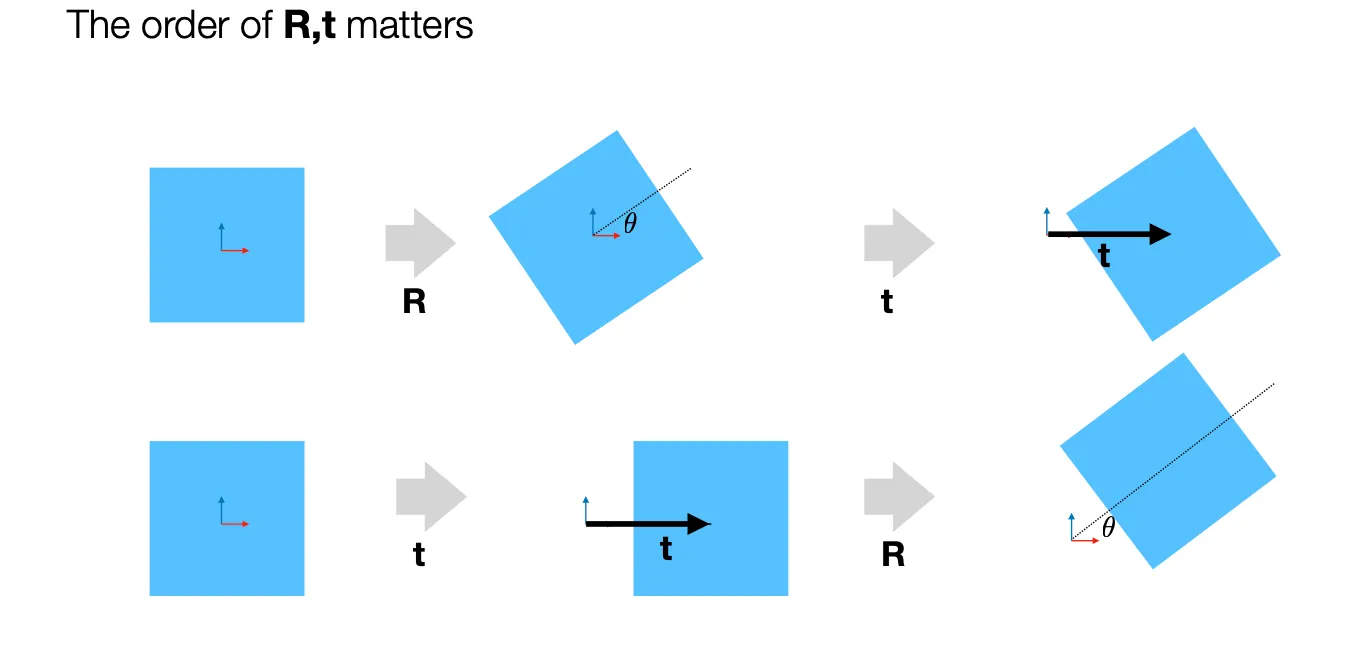
Rotation 의 중심에 따라서 결과가 달라짐.
◦
위 결과 때문에 Rotation 과 Translation 의 순서에 따라서 결과가 달라짐.
•
일반적으로 Rotation First, Translation Later 를 따름.

A Hierarchy of Transformations: Isometries

x′=[ϵcos⁡θ−sin⁡θtxϵsin⁡θcos⁡θty001]{\rm x'} = \begin{bmatrix} \epsilon\cos\theta & -\sin\theta & t_x \\ \epsilon\sin\theta & \cos\theta & t_y \\ 0 & 0& 1 \end{bmatrix}
•
Euclidean Transform 에서 ϵ\epsilon term 이 추가된 경우임.
•
ϵ=±1\epsilon = \pm1
•
ϵ=−1\epsilon=-1 인 경우는 reflection 이 포함된 transformation 으로 볼 수 있음.
•
길이, 각도, 영역이 유지됨.

A Hierarchy of Transformations: Similarities

x′=[sR2×2t02×11]x=[scos⁡θ−ssin⁡θtxssin⁡θscos⁡θty001]x{\rm x'} = \begin{bmatrix} {\rm sR}_{2\times 2} & {\rm t} \\ {\rm 0}_{2\times 1} & 1 \end{bmatrix}{\rm x} = \begin{bmatrix} s\cos\theta & -s\sin\theta & t_x \\ s\sin\theta & s\cos\theta & t_y \\ 0 & 0& 1 \end{bmatrix}{\rm x}
•
Euclidean Transform 에서 ss term 이 추가된 경우임.
•
ss 는 scaling factor 로 확대/축소가 가능함.
•
4DoF: 1DoF for t{\rm t} + 2DoF for R{\rm R} + 1DoF for ss
•
각도가 유지됨.

A Hierarchy of Transformations: Affine

x′=[A2×2t02×11]x=[a11a12txa21a22ty001]x{\rm x'} = \begin{bmatrix} {\rm A}_{2\times 2} & {\rm t} \\ {\rm 0}_{2\times 1} & 1 \end{bmatrix}{\rm x} = \begin{bmatrix} a_{11} & a_{12} & t_x \\ a_{21} & a_{22} & t_y \\ 0 & 0& 1 \end{bmatrix}{\rm x}
•
AA 는 Non-Singular Matrix (Invertible)
•
6DoF: 4 for AA + 2 for t{\rm t}
◦
세 번째 요소를 계산할 때 Up-to-Scale 하지 않음.
•
Parallelism 이 유지됨.
◦
두 평행한 선의 교점 (Ideal Point)을 Affine Transformation 하면 항상 Ideal Point 인 것을 통해 증명할 수 있음. (Invariance of Ideal Point)
[a11a12txa21a22ty001][x1x20]=[x1′x2′0]\begin{bmatrix} a_{11} & a_{12} & t_x \\ a_{21} & a_{22} & t_y \\ 0 & 0& 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2\\ 0 \end{bmatrix} = \begin{bmatrix} x_1' \\ x_2' \\ 0 \end{bmatrix}
◦
Line at Infinity 또한 마찬가지로 Line at Infinity 로 mapping 됨.
▪
Homography Matrix of Point 의 inverse transpose 가 line 끼리의 변환임을 사용함.
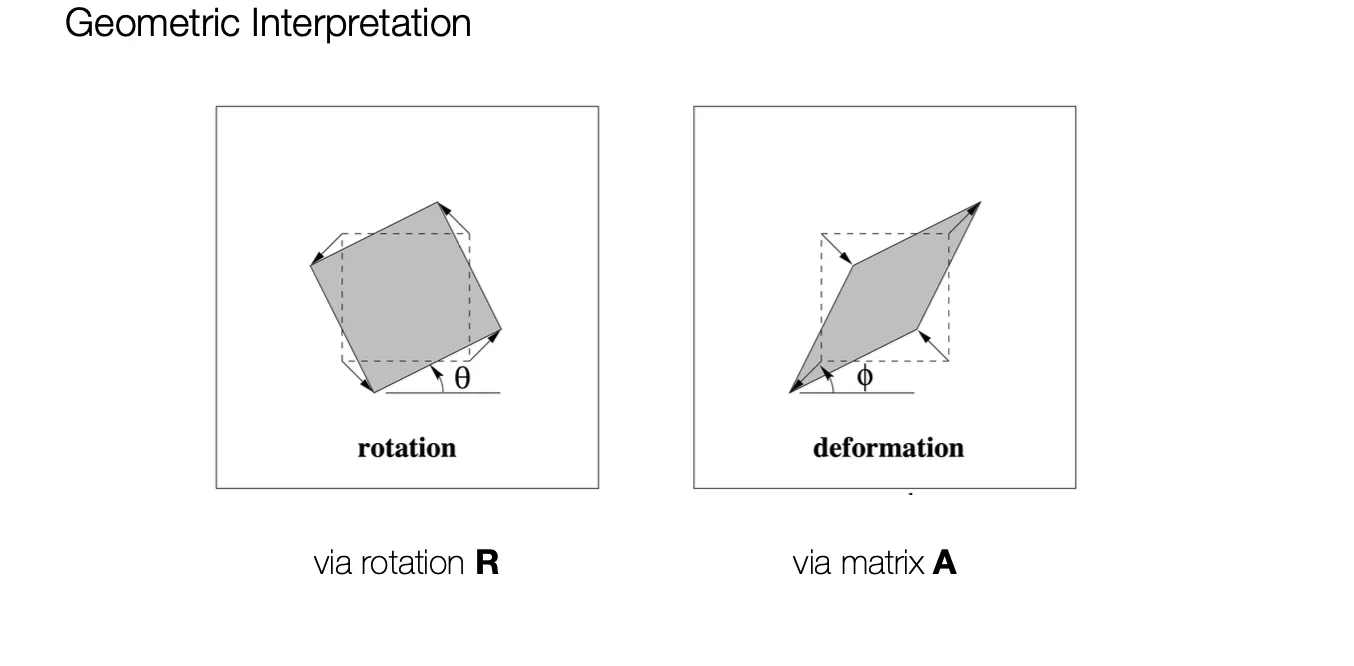
l′∞=[A−T0−tTA−T1][001]=[001]=l∞{\rm l'}_{\infty} = \begin{bmatrix} {\rm A}^{-T} & 0 \\ -{\rm t}^T{\rm A}^{-T} & 1 \end{bmatrix} \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} = {\rm l}_{\infty}
•
AA 는 일반적으로 다음과 같이 표현될 수 있음.
A=R(θ)R(−ϕ)DR(ϕ)whereD=[λ100λ2]{\rm A} = R(\theta)R(-\phi)DR(\phi) \\ \quad \\ {\rm where}\quad D = \begin{bmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \end{bmatrix}
◦
먼저 θ\theta 만큼 회전시킨 뒤에, 특정 방향 (ϕ\phi) 으로 Scaling 하는 것을 의미함.
◦
다음과 같이 SVD 로 각 항목을 분해할 수 있음.
A=UDVT=(UVT)(VDVT)=R(θ)R(−ϕ)DR(ϕ)A = UDV^T = (UV^T)(VDV^T)= R(\theta)R(-\phi)DR(\phi)

A Hierarhcy of Transformations: Projective Transformations

x′=[Atv2×1v]x{\rm x'} = \begin{bmatrix} {\rm A} & {\rm t} \\ {\rm v}_{2\times1} & v \end{bmatrix} {\rm x}
•
8DoF: 9 variables - 1DoF for Up-to-Scale
•
vv 는 0 이 될 수 있음.
•
Colinearity, Cross-Ratio 가 유지됨.

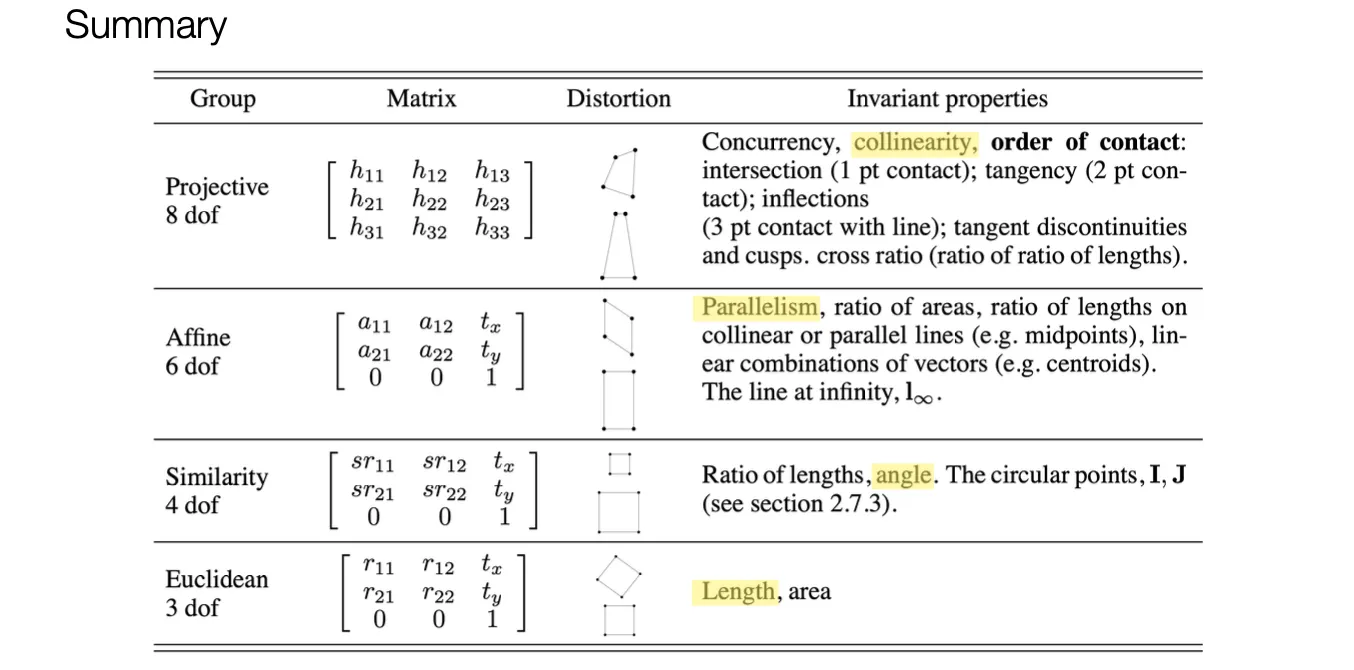
A Hierarhcy of Transformations: Summary

\