Point Cloud Upsampling via Disentangled Refinement

리뷰 날짜
2022/05/13
분야
Point Cloud Upsampling
본 포스트에서는 Point Cloud Upsampling 분야에서 새로운 방법론을 제시한 논문에 대해서 소개드리려고 합니다. 리뷰하려는 논문의 제목은 다음과 같습니다.
“Point Cloud Upsampling via Disentangled Refinement”
논문에 대한 내용을 직접 보시고 싶으신 분은 이곳을 참고하시면 좋습니다.

Objective

Point Cloud 는 자율주행, 로보틱스, 렌더링, 의료 분석 등 많은 어플리케이션에서 3D data 를 compact 하게 표현할 수 있는 방법으로 사용되고 있습니다. 이러한 Point Cloud 는 일반적으로 3D scanning 이라는 방법을 통해서 생성되는데 이렇게 생성된 Point Cloud 데이터는 아래 그림의 (a)(a) 와 같이 종종 밀집되어 있지 못하고 균일하지도 않은 특성을 보입니다.
Point Cloud Upsampling
Point Cloud Upsampling 은 이러한 Point Cloud 의 단점을 극복하기 위한 분야입니다. 하지만, 단순히 sparse 한 input point cloud 로 부터 dense 한 point cloud 를 생성해내는 task 는 아닙니다. 논문에서는 효과적인 upsampling 을 위해서는 다음과 같은 두 가지 제약조건이 필연적이라고 거듭하여 강조하고 있습니다.
1.
생성된 Point 들이 underlying surface 에 잘 놓여 있어야 하고, (Proximity-To-Surface)
2.
Point 들이 underlying surface 에 놓여있는 분포가 균일해야 한다 (Distribution Uniformity)
머신러닝과 딥러닝 덕에 traditional 한 방법론을 성능에서 압도하는 여러가지 선행연구들이 이미 나왔고, 이들은 대부분 하나의 네트워크에서 (1)(1) dense 하면서도, (2)(2) underlying surface 에 faithfully 하게 놓여있고, (3)(3) 그 surface 위에서 균일하게 분포되어 있는 Point Cloud 를 생성하려고 했습니다. 하지만, 이러한 요구사항을 하나의 네트워크에서 모두 달성하기에는 매우 어려웠고 일반적으로 dense 한 point cloud 를 형성하기는 했지만 non-uniform 하고 noise 가 포함되어 있는 결과물들이 많이 등장했습니다.
논문에서는 이러한 상황에서 task 를 두 가지로 분리하는 아이디어를 제시합니다. (1)(1) coarse 하지만 dense 한 Point Cloud 를 형성해주는 task 와 (2)(2) 앞선 task 로 생성한 Point Cloud 가 underlying surface 에 균일하게 놓이도록 조정하는 task 로 나눕니다.

Method

앞서 잠깐 언급드린 것처럼 논문에서는 기존에 다양한 조건들을 하나의 네트워크 속에서 달성하기 위한 시도로부터 벗어나 upsampling task 자체를 두 개의 목표로 분리합니다. (1)(1) Coarse 하지만 dense 한 Point Cloud 를 생성하는 것과 (2)(2) 생성한 Point Cloud 의 Proximity-To-Surface 및 Distribution Uniformity 를 증가시키는 것이 그 두 목표입니다.
Two Cascaded Sub-Networks
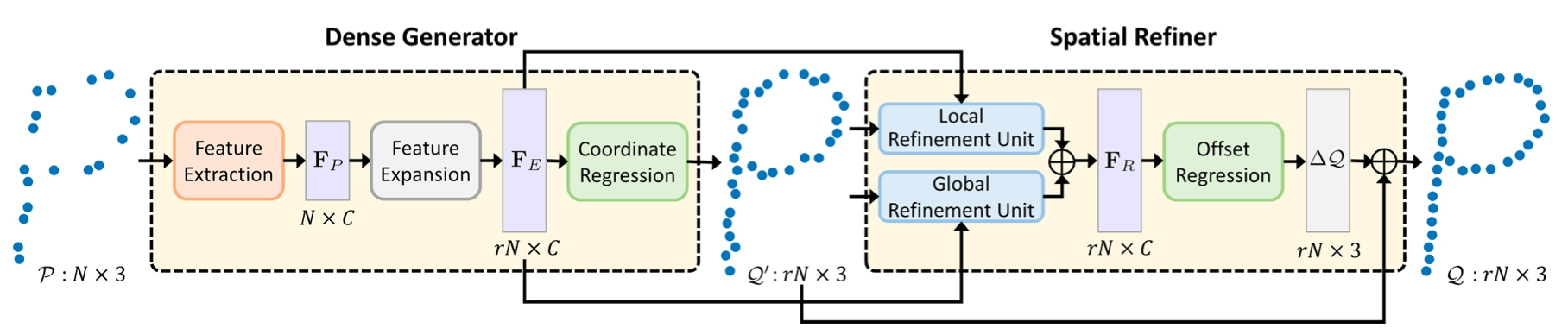
논문에서는 각각의 목표를 달성하기 위한 네트워크의 구조로 two cascaeded sub-networks 를 제안합니다. 이어진 각각의 network 가 각각의 목표를 달성하기 위해 사용된다고 보시면 됩니다. 논문에서는 이 두 네트워크를 각각 Dense Generator 와 Spatial Refiner 라고 명명합니다.

Dense Generator

Dense Generator 는 Spatial Refiner 의 존재 때문에 간단한 목표만을 가져갈 수 있게 됩니다. 네트워크의 이름대로 Sparse Point Cloud 를 단순히 dense 하게만 만들면 됩니다. 물론 완전 의미없는 위치의 point 들을 생성하면 안됩니다. 하지만, roughly 하게 surface 에 underlying 하는 Point Cloud 정도를 생성하는 것을 목적으로 학습을 진행할 수 있게 됩니다. 이렇게 간소화된 목표를 통해 학습 결과가 유연하게 나와도 상관이 없게 되고 네트워크가 복잡할 필요가 없으며 상대적으로 높은 upsampling rate 를 가져가기가 쉬워졌다고 합니다.
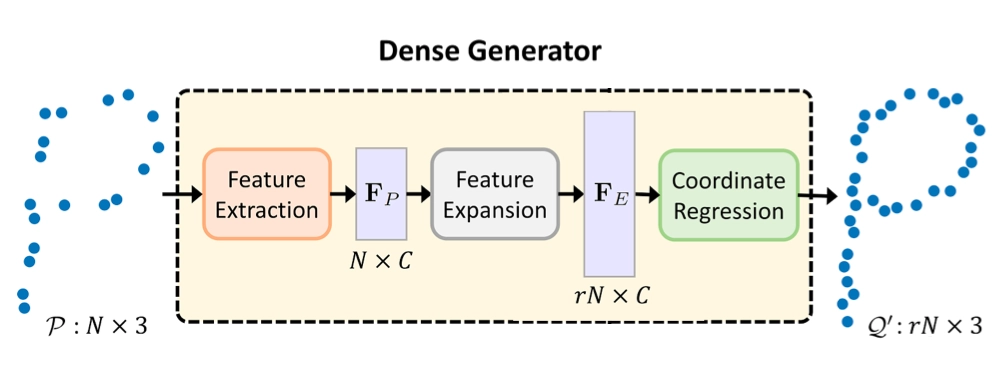
Dense Generator
위 그림과 같이 Dense Generator 의 input 은 x,y,zx, y, z 로 3개의 coordinate 를 가진 Point N 개입니다. Dense Generator 내부는 Feature Extractor, Feature Expansion, Coordinate Regression 로 이루어져 있으며, input 은 이들을 거쳐서 최종적으로 γ\gamma 배가 된 Point 를 output 으로 변환되어 반환됩니다. 이 때 tensor 는 N×3N\times 3 에서 γN×3\gamma N\times 3 이 됩니다. 다음은 Dense Generator 를 이루는 각각의 방법론들에 대한 설명입니다.
Feature Extractor
Feature Extractor
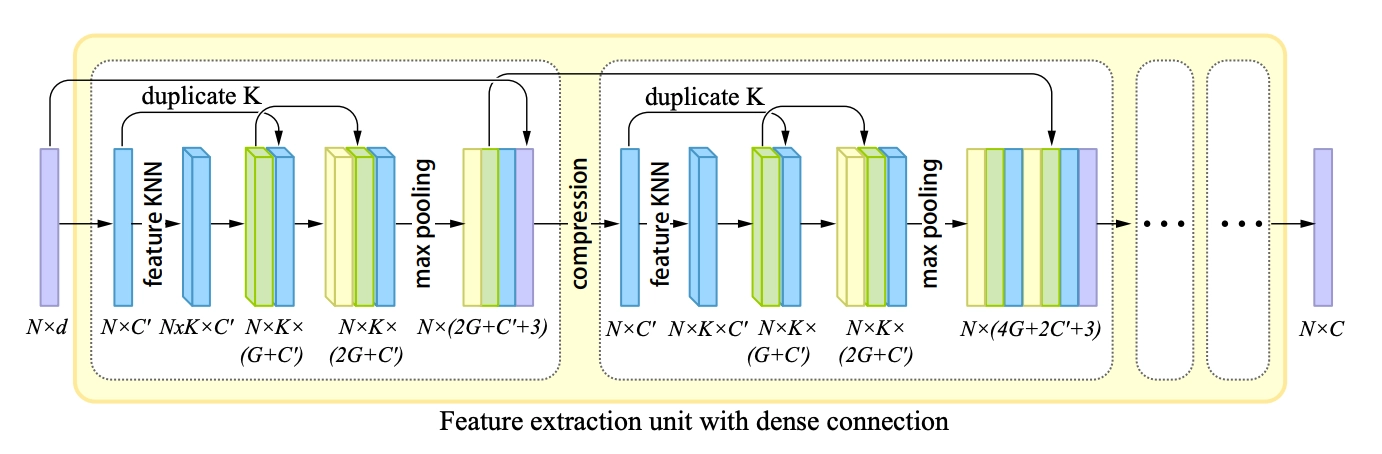
Feature Extractor 는 Patch-based progressive 3D point set upsampling 논문에서 제시한 네트워크의 구조를 차용하고 있습니다. 해당 논문에서 제시한 feature extractor 는 그림처럼 dense block 의 sequence 로 구성되어 있습니다. 각각의 dense block 은 input tensor 를 고정된 CC 개의 feature 로 변환시켜주는 역할을 합니다.
Dense block 의 첫 번째 과정은 feature-based KNN 으로 feature 를 grouping 하는 과정입니다. 이는 Spatial Refiner 에서도 설명할 내용인데, NN 개의 point set 각각에 대해서 가장 가까운 KK 개의 point 들을 grouping 하여 명시적으로 근접한 데이터임을 feature 에 반영하는 방법이라고 보시면 됩니다. 하나의 group 은 KK 개의 point 들을 포함하고 있고 group 은 처음에 레퍼런스로 들어온 point set 의 개수인 NN 개만큼 있고, 각 point 의 channel 은 C′C' 개이므로 전체 tensor 의 dimension 이 N×K×C′N\times K\times C' 이 되는 것입니다.
여기서 NN 개의 Point 들만으로 KK 개의 point 를 포함한 NN 개의 group 을 만들면 중복된 point 들이 생길수도 있지 않나? 라고 생각하실 수 있습니다. 결론부터 말씀드리자면 생길 수 있습니다. 다만 앞서 설명드린 것처럼 feature 에 직접적으로 가까운 데이터임을 명시적으로 드러내어 학습에 용이한 feature 로 정제하기 위한 하나의 과정으로 이해하시는 것이 좋습니다.
Dense block 의 두 번째 과정은 densely-connected MLP 로 feature 를 refining 하는 과정입니다. 이 때 사용하는 MLP 의 output feature 의 개수는 GG 개이며, skip connection 을 통한 tensor concatenate 를 통해 explicit 하게 정보를 재사용하는 효과를 기대했고 결과적으로 reconstruction accuracy 를 높이려고 했다고 합니다. 때문에 한 번의 MLP 를 거쳤을 때 나오는 tensor 의 dimension 은 KK 개로 복제된 입력 K×K×C′K\times K\times C' 에 MLP 로 나온 output dimension 인 N×K×GN\times K\times G 를 더해 N×K×(G+C′)N\times K\times (G+C') 가 되는 것입니다. 이를 두 번 반복하게 되면 다시 또 N×K×GN\times K\times G 가 더해진 N×K×(2G+C′)N\times K\times (2G+C') 가 나오게 됩니다.
Dense block 의 세 번째 과정은 Max-Pooling 과정입니다. 전체 tensor 를 KK 개의 tensor 로 바라보았을 때 하나의 값을 pooling 각각의 tensor 내에서 하나의 값을 pooling 하도록 하고, 마찬가지로 제일 처음의 tensor 로부터의 skip conection 이 존재하여 이 제일 처음의 tensor 의 채널 수를 3 이라고 할 때 최종적으로는 N×(2G+C′+3)N\times (2G+C'+3) 의 dimension 이 나오게 됩니다.
추가적으로 두 번째 dense block 부터는 이전 dense block 의 마지막 feature 로부터의 skip connection 이 추가적으로 생기기 때문에 두 번째 dense block 의 경우 위의 그림처럼 N×(2G+C′+3)N\times (2G+C'+3) 과 max-pooling 된 N×(2G+C′)N\times (2G+C') 이 더해진 N×(4G+2C′+3)N\times (4G+2C'+3) 이 됩니다. 그리고 적혀있지는 않지만 세 번째 dense block 의 경우 N×(6G+3C′+3)N\times (6G+3C'+3) 이 될 것임을 계산해볼 수 있을 것입니다.
Feature Expainsion
Feature Expansion 은 일반적으로 많이 사용되는 expansion operation 을 사용했다고 합니다. 이는 단순하게 기존의 feature 를 γ\gamma 배만큼 duplicate 하는 방식으로, channel 수가 늘지 않고, 동일한 채널을 가지는 데이터의 수가 많아지도록 설계했습니다. 즉 feauture expansion 을 통해 기존의 N×CN\times C dimension 의 tensor 를 γN×C\gamma N\times C 로 변경했습니다.
Coordinate Regression
Coordinate Regression 은 논문에서도 중요하게 다루지는 않았습니다. MLP 를 통해 구현했다고 하고, CC 개의 channel 을 가진 tensor 를 다시 point cloud 로 변환하기 위해 3개의 channel 로 regression 을 진행하는 과정이라고 보시면 됩니다.
이렇게 세 개의 방법론들에 대해서 알아보았습니다. 하지만, Coordinate Regression 까지 거쳐서 나온 point cloud 데이터 Q′Q' 은 여전히 non-uniform 및 noisy 한 특성을 가지고 있었기 때문에, 이어서 설명드릴 Spatial Refiner 에서 이러한 현상을 해결합니다.

Spatial Refiner

Spatial Refiner 는 앞서 설명드린 것과 같이 non-uniform 하고 noisy 한 point cloud 데이터인 Q′Q' 을 underlying surface 에 균일하게 놓여있도록 조정하는 역할을 합니다.
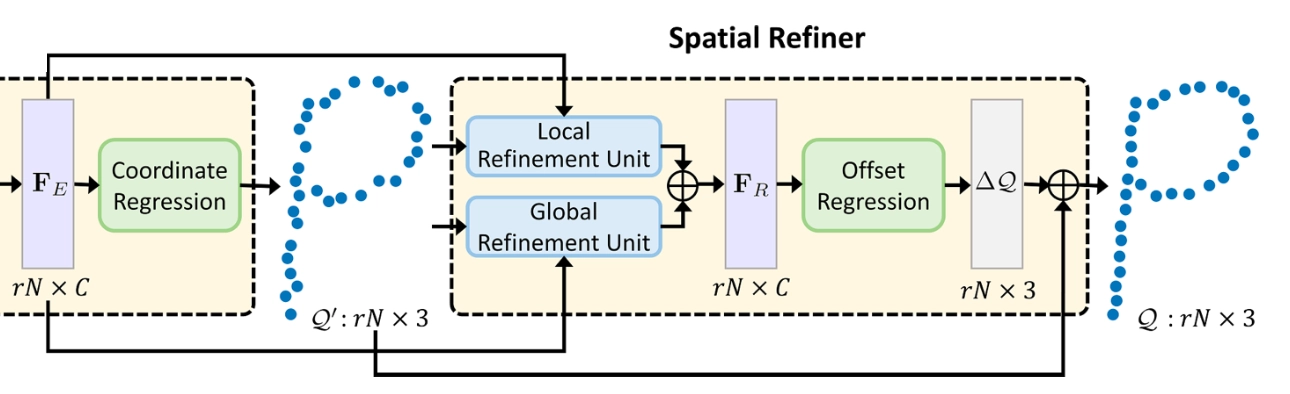
Spatial Refiner
위 그림과 같이 Spatial Refiner 의 input 은 non-uniform 하고 noisy 한 point cloud 데이터입니다. Spatial Refiner 내부는 (Local & Global) Refinement Unit, Offset Regression 으로 이루어져 있으며, input 은 이들을 거쳐서 최종적으로 refined 된 point 로 변환되어 반환됩니다. 이 때 tensor 의 크기에는 변화가 없습니다. 다음은 Spatial Refiner 를 이루는 각각의 방법론들에 대한 설명입니다.
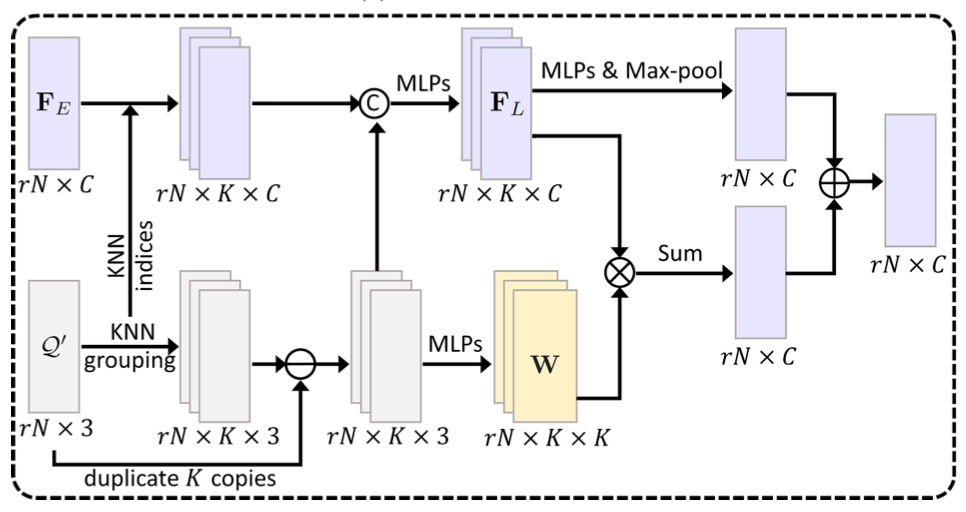
Local Refinement Unit
Local Refinement Unit 은 point cloud 의 local geometric structure 를 고려한 형태의 조정을 위해 설계된 네트워크입니다. 이러한 local geometric structure 를 반영하기 위해 논문에서는 앞서 feature extractor 에서 사용했던 feature-based KNN 을 사용합니다.
Local Refinement Unit
앞서 feature-based KNN 은 NN 개의 point set 각각에 대해서 가장 가까운 KK 개의 point 들을 grouping 하여 명시적으로 근접한 데이터임을 feature 에 반영하는 방법이라고 말씀드렸습니다. 여기서도 Q′Q' 에 대해 해당 방법을 적용하고 근접한 데이터에서 복제된 reference point 를 빼는 형태로 가까운 point 들 사이의 거리에 대한 feature 를 생성하게 됩니다. 이 때, Q′Q' 에서만이 아니라 앞선 Dense Generator 의 feature 인 FEF_E 에 대해서도 tensor 상에서 동일한 위치의 값들이 인접하다- 라는 가정하에 index 를 그대로 끌고 와서 확장된 tensor 를 만들게 됩니다.
이후 앞선 Q′Q' 의 KNN 으로부터 index 를 받아 FEF_E 가 확장된 γN×K×C\gamma N\times K\times C dimension 의 tensor 는 가까운 거리에 대한 feature 와 concatenate 되어 MLP 를 거쳐서 새로운 feature 인 FLF_L 을 생성하게 됩니다. 이를 논문에서는 encoded feature volume 이라고 명명하는데, 저는 기존에 Dense Generator 단에서 생성된 크기가 큰 feature vector 에 nearest neighbor 에 대한 정보를 추가하여 local region 에 대한 국소적인 정보들을 volume 형태로 담고 있는 feature 라고 이해했습니다.
이렇게 생성된 FLF_L 로부터 최종적인 local point feature 를 얻어내기 위해서 MLP 및 max-pooling 을 거치게 되는데, 또 point 들 사이의 거리에 대한 feature 로부터 spatial weight 라고 부르는 WW 값을 구하기 위해 MLP 를 사용한다고 합니다. FLF_L 과 WW 사이의 convolution 연산 이후에 생성된 tensor 와 FLF_L 에서 MLP 및 max-pooling 을 거쳐 얻은 tensor 모두 γN×C\gamma N\times C 의 dimension 을 가지고 이에 대한 summation 으로 최종적인 local point feature 를 얻어내게 됩니다. 논문에서 이 부분에 대한 자세한 설계 이유를 제공해주지는 않고 있습니다만, 우선 local region volume 에 대한 feature 의 생성 이후 MLP 및 nearest neighbor 에 대한 정보의 재사용으로 최종적인 feature 를 완성하는 형태로 구현하여 local geometric strucuture 를 나타낼 수 있는 정보를 담을 수 있는 설계를 진행한 것으로 보입니다
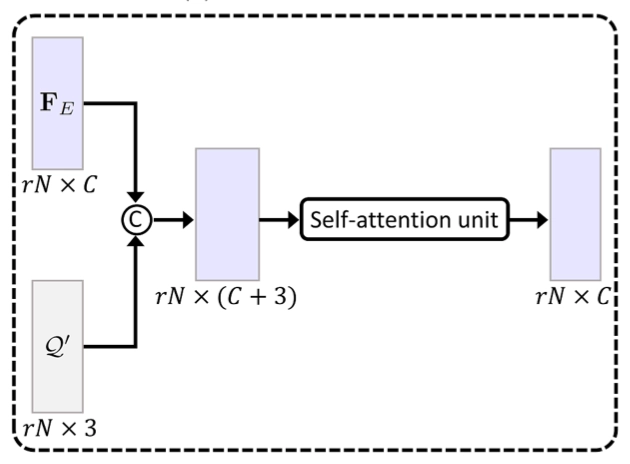
Global Refinement Unit
Global Refinement Unit 은 point cloud 의 overall shape strucuture 를 고려한 형태의 조정을 위해 설계된 네트워크입니다. 여기서는 Self-attention generative adversarial networks 논문에서 self-attention unit 을 차용하여 썼다고 합니다.
Global Refinement Unit
전체적인 point cloud 의 모양을 고려한 형태의 조정을 위해서 모든 shape strucuture 에 관한 정보를 잃지 않기 위해 FEF_E 와 Q′Q' 데이터를 직접적으로 concatenate 했다고 합니다. 그렇게 생겨난 γN×(C+3)\gamma N\times (C+3) 의 tensor 는 self-attention unit 에 들어가서 global feature map 을 산출하게 됩니다. 이러한 self-attention unit 의 사용은 모든 γN\gamma N 개의 point 들 사이의 attention weight 를 구하기 때문에 long-range context dependency 도 반영할 수 있고 전체적인 모양에 대한 feauture 를 형성할 수 있다고 합니다.
Offset Regression
절대적인 3D point 의 위치를 regression 을 통해 알아내는 것의 자유도와 범위가 크기 때문에 어렵습니다. 이에 비해서 범위 및 자유도가 적은 잔차는 학습하기 용이합니다. 이 때문에 네트워크에서는 ground truth 와 비교했을 때의 잔차를 학습하는 형태로 Offset Regression 을 진행하게 됩니다. 이렇게 구해낸 잔차를 기존의 입력 point cloud 인 Q′Q' 에 더함으로써 최종적인 point cloud 의 형태를 얻어냅니다.

Patch-based End-to-end Training

앞서는 네트워크 구조를 기반으로 한 방법론에 대해서 알아보았습니다. 하지만 논문에서는 loss 관련해서도 특별하게 사용한 방법론을 설명합니다.
네트워크의 학습 과정 중에서는 특정한 sparse point cloud PP 에 대해서 coarse 하지만 dense 한 point cloud Q′Q' 와 최종적인 prediction point cloud 인 QQ 가 생성됩니다. 논문에서는 다른 여타 upampling approach 에서 그랬듯, PP 에 해당되는 ground truth point cloud Q^\hat Q 에 대해서 논문에서는 두 point cloud 모두를 penalize 할 수 있는 loss 를 설계합니다.
L=LCD(Q′,Q^)+λLCD(Q,Q^)L=L_{CD}(Q',\hat Q)+\lambda L_{CD}(Q,\hat Q)
이 때, LCDL_{CD} 는 Chamger Distance 로 LCD(Q′,Q^)L_{CD}(Q',\hat Q) 의 경우에는 Q′Q' 내의 point 들 각각에 대해서 Q^\hat Q 에서 찾을 수 있는 가장 가까운 point 와의 distance 에 대한 평균이라고 보시면 됩니다. λ\lambda 는 LCD(Q′,Q^)L_{CD}(Q',\hat Q) 와 LCD(Q,Q^)L_{CD}(Q,\hat Q) 사이의 가중치를 조정하는 요소이며, 학습의 초반 부에는 작은 λ\lambda 값을 주어 Q′Q' 이 그럴듯하게 나올 수 있도록 유도하고 점차 λ\lambda 값을 키워서 Spatial Refiner 가 학습될 수 있도록 유도했다고 합니다.

Experiments & Results

Experimental Settings

Datasets
논문에서는 synthetic daasets 과 real-scanned datasets 모두를 이용하여 그들의 방법론이 효과적이었음을 보여줍니다. Synthetic datasets 는 PointPillars: Fast encoders for object detection from point clouds 에서 제공한 120 개의 training datasets 과 27 개의 testing datasets 을 사용했다고 합니다.
Training datasets 로는 제공한 120 개의 training datasets 하나 당 200 개의 겹쳐진 patch 들로 cropping 하여 사용했습니다. 그 결과 총 24000 개의 training datasets 을 얻을 수 있었고 각각의 training dataset 에서 γN\gamma N point 만을 균일하게 sampling 하여 ground truth Q^\hat Q 를 구성했습니다. 이후, 이를 랜덤하게 downsampling 하여 PP 를 구성했다고 합니다.
Test datasets 로는 MPU 와 PU-GAN 등을 따라서 poisson disk sampling 을 통해 20,000 개의 uniform points 인 Q^\hat Q 를 얻어낸 뒤, 1024 개의 non-uniform points 를 그 속에서 생성해내 PP 를 구성했다고 합니다.
Real-scanned datasets 으로는 각각이 2048 개의 point 로 이루어진, 15 개의 카테고리 내에서 2902 개의 point cloud objects 를 보유하고 있는 ScanObjectNN 을 사용했습니다. 다만, ScanObjectNN 에서는 dense points 를 제공해주지 않기 때문에 논문에서는 이 datasets 을 test 할 때만 활용했다고 합니다.
Evalutation metrics
정량적인 평가를 위해 논문에서는 다음 세가지 evaluation metric 을 사용합니다. 각각에 대한 설명은 다음과 같습니다.
1.
Chamfer distance 한 point cloud 내의 모든 point 들에 대해서 다른 point cloud 내의 point 중 해당 point 와 가장 가까운 거리를 가지는 point 와의 거리들의 평균값을 계산한 evalutaion metric
2.
Hausdorff distance 한 point cloud PP 내의 모든 point 들에 대해서 다른 point cloud QQ 내의 point 중 해당 point 와 가장 가까운 거리를 가지는 point 와의 거리가 최대가 되는 point 에 대해서 그 거리의 값을 d1d_1 과 반대로 point cloud QQ 를 기준으로 point cloud PP 에서 동일한 작업을 했을 떄 나오는 거리의 값을 d2d_2 라고 했을 때 max⁡(d1,d2)\max(d_1,d_2) 를 계산한 evaluation metric
3.
Point-to-surface distance 이 metric 에 대한 구체적인 설명 및 자료가 불충분했지만, 저는 우선 point cloud 속 point 각각에 대해서 underlying surface 와의 거리들의 평균값을 계산한 evaluation metric 정도로 이해했습니다.
Comparison methods
논문에서 제시한 방법론의 효과를 보여주기 위해 논문에서는 point cloud upsampling 분야에서 SOTA 를 보여준 PU-Net, MPU, 그리고 PU-GAN 과의 비교를 시도합니다. 논문에서 준비한 training data 로 그들의 논문에서 제시한 setting 을 따라서 재학습을 진행했고 PUGeoNet 같은 경우는 코드를 사용할 수 없었기 때문에 comparison result 를 제공하진 못했다고 합니다.
Implementation details
논문에서 제시한 구현체의 세부적인 사항은 다음과 같습니다.
1.
Input point cloud 의 point 의 개수 N 을 256 으로 설정했습니다.
2.
TensorFlow 환경에서 batch size 는 28 이고, 400 epoch 동안 학습을 진행했습니다.
3.
Overfitting 을 방지하기 위해 random scaling, rotation, point perturbation 을 사용했습니다.
4.
Adam optimizer 를 사용했고, 초기 learning rate 는 10−310^{-3} 이며 10−610^{-6} 에 도달할 때까지 40 epoch 당 0.7 배로 낮추었습니다.
5.
설계한 loss 식에서 나타난 상수 λ\lambda 는 0.01 에서 1.0 까지 linear 하게 증가시켰습니다.

Results on Real-scanned Dataset

논문에서는 Real-scanned datasets 을 input 으로 하여 평가한 결과를 아래의 그림과 같이 정성적으로 보여줍니다. Real-scanned datasets 에 대한 정량적 분석은 논문에서 진행하지는 않습니다.
Real-Scanned Datasets: Qualitative Results
(a)(a) 의 각 row 의 상단 point cloud 를 보면 굉장히 sparse 하고 non-uniform 한 것을 확인할 수 있습니다. 이 때문에 The ball-pivoting algorithm for surface reconstruction 에서 제시한 알고리즘을 활용해 3D Mesh 로 변환하더라도 구멍이 보이는 불완전한 모습이 보이는 것을 관찰할 수 있습니다.
기존의 upsampling 방법론 (b),(c)(b), (c) 활용한 upsampled results 들은 결과물에 noise 가 있거나 균일한 output 을 만들어어내지 못했고, 이러한 point cloud 결과물은 reconstructed mesh 로 변환했을 때 거친 표면을 만들어내거나 작은 구멍들을 포함하고 있었습니다.
반면, 논문의 upsampling 방법론 (d)(d) 는 uniform, dense 한 point 들을 생성해내는 것을 확인할 수 있었고 때문에 3D mesh 로 변환했을 때의 기하학적 구조도 smooth 하고 구멍이 없이 완전한 것을 볼 수 있었습니다.

Results on Synthetic Dataset

논문에서는 Synthetic datasets 을 input 으로 하여 평가한 결과를 아래의 그림과 같이 정성적으로 보여줍니다.
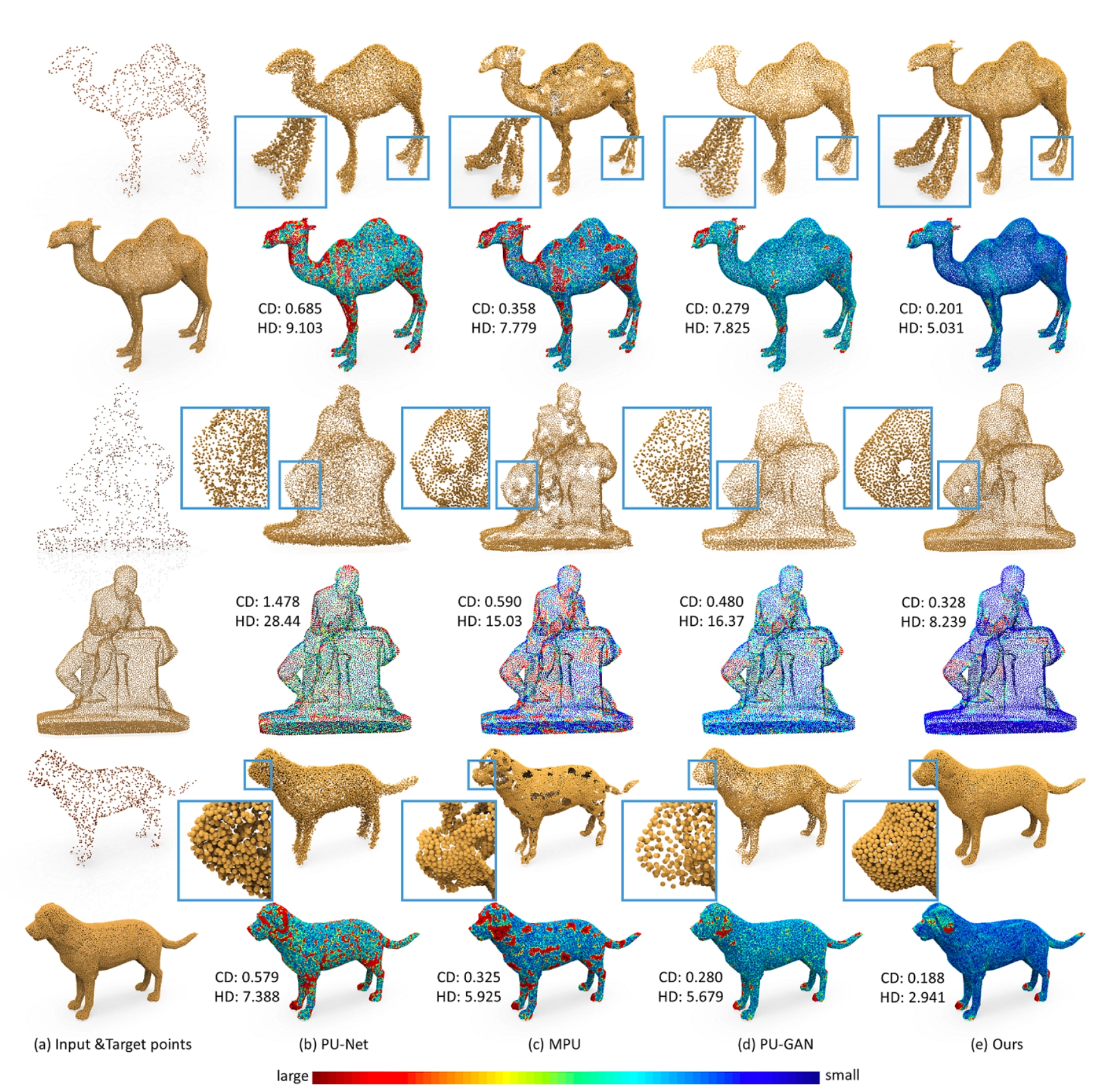
Synthetic Datasets: Qualitative Results
위의 그림은 (a)(a) 의 input 과 target point 를 기반으로 기존의 방법론과 논문의 방법론이 산출해낸 결과를 비교한 것입니다. (b)(b) 의 경우에는 noise 가 심한 것을 확인할 수 있으며, (c)(c) 의 경우에는 non-uniformity 를 확인할 수 있습니다. (d)(d) 의 경우는 tiny structure 에 대한 destruction 을 볼 수 있습니다.
이와 달리 논문의 (e)(e) 는 target point 와 굉장히 유사한 시각적 결과를 볼 수 있으며 논문의 방법론이 생성해낸 dense points 들은 local structure 를 균일하게 표현해낼 수 있었습니다.
더불어 아래의 푸른색 느낌의 point cloud 는 error map 을 의미하는데, 생성해낸 point cloud 속의 각각의 point 와 target cloud 의 point 와의 최소 거리에 따라 색깔을 다르게 표현한 것입니다. 논문의 (e)(e) 가 작은 쪽에 속하는 푸른 빛깔이 가장 강한 것을 확인할 수 있었습니다.
논문에서는 Synthetic datasets 을 input 으로 하여 평가한 결과를 아래의 그림과 같이 정량적으로도 보여줍니다.
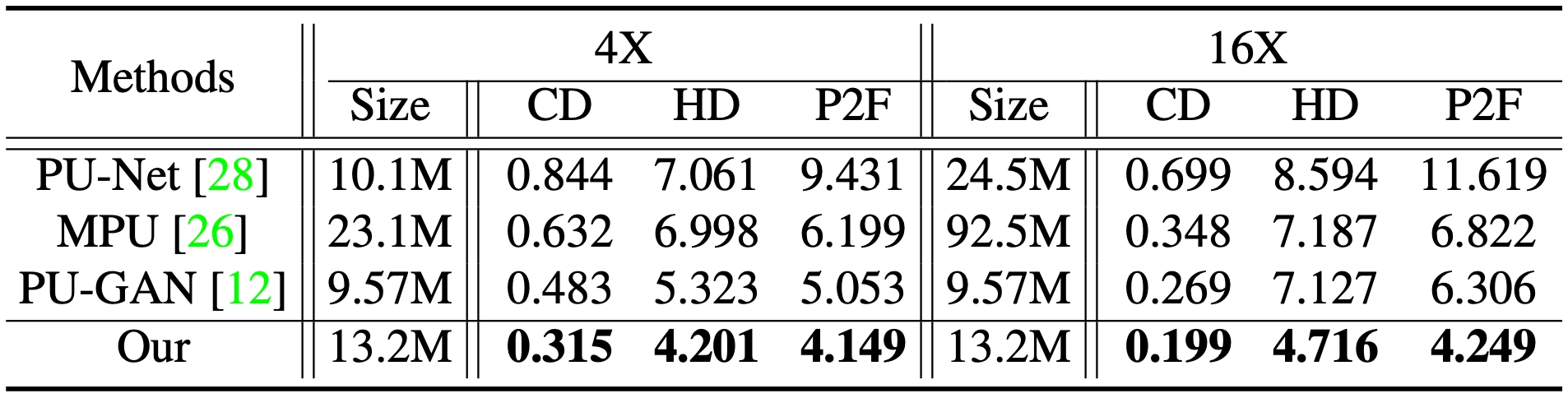
Synthetic Datasets: Quantitative Results
앞서 말씀드렸던 3 개의 evaluation metric 을 사용했고, 모두 PU-Net, MPU, PU-GAN 을 제치고 논문의 방법론이 모든 metric 에서 가장 작은 값을 보였음을 알 수 있습니다. 더불어 논문의 방법론이 기존의 방법론과의 특징적인 차이점은 upsampling rate γ\gamma 에 관계없이 일정한 parameter 수를 보인다는 점입니다. 이는 Dense Generator 에서 보여준 특징적인 Feature Expansion 때문인데 MLP 를 사용하지 않고 단순히 duplicated 하여 데이터를 upsampling 한 뒤에 regression 을 했기 때문에 γ\gamma 의 조정에 따른 parameter 수의 변화가 없는 것입니다.

Noise Robustness Test

논문에서는 설계한 방법론이 얼마나 noise 한 input point cloud 에 대해서 robust 한지에 대한 내용도 평가하여 보여줍니다. 아래는 논문에서 정성적 및 정량적으로 보여준 결과입니다.
Noise Robustness Test: Qualitative Results
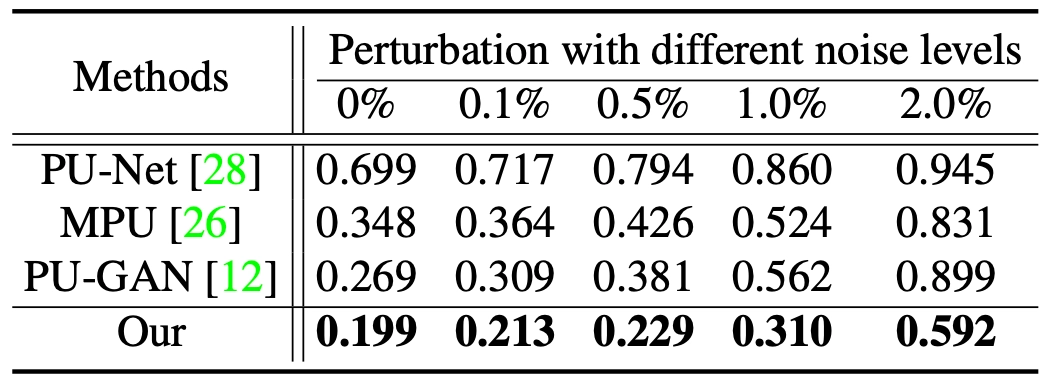
Noise Robustness Test: Chamfer Distance
두 개의 upsampling rate 모두에서 논문의 방법론이 과도한 noise 의 증가 없음을 정성적으로 확인할 수 있었습니다. 더불어 Chamfer Distance 기준에서도 noise 수준이 어떻든 간에 다른 방법론들에 비해서 좋은 metric 수치를 보여주었고 noise level 증가에 따른 metric 의 증가폭도 적었음을 볼 수 있었습니다.

Ablation Test

마지막으로, 논문에서는 그들이 세부적으로 설계한 방법론들이 실제로 효과가 있었음을 보여주기 위해 각각을 제거한 상태로 evaluation 을 진행한 결과를 보여줍니다. 그 결과는 다음과 같습니다.
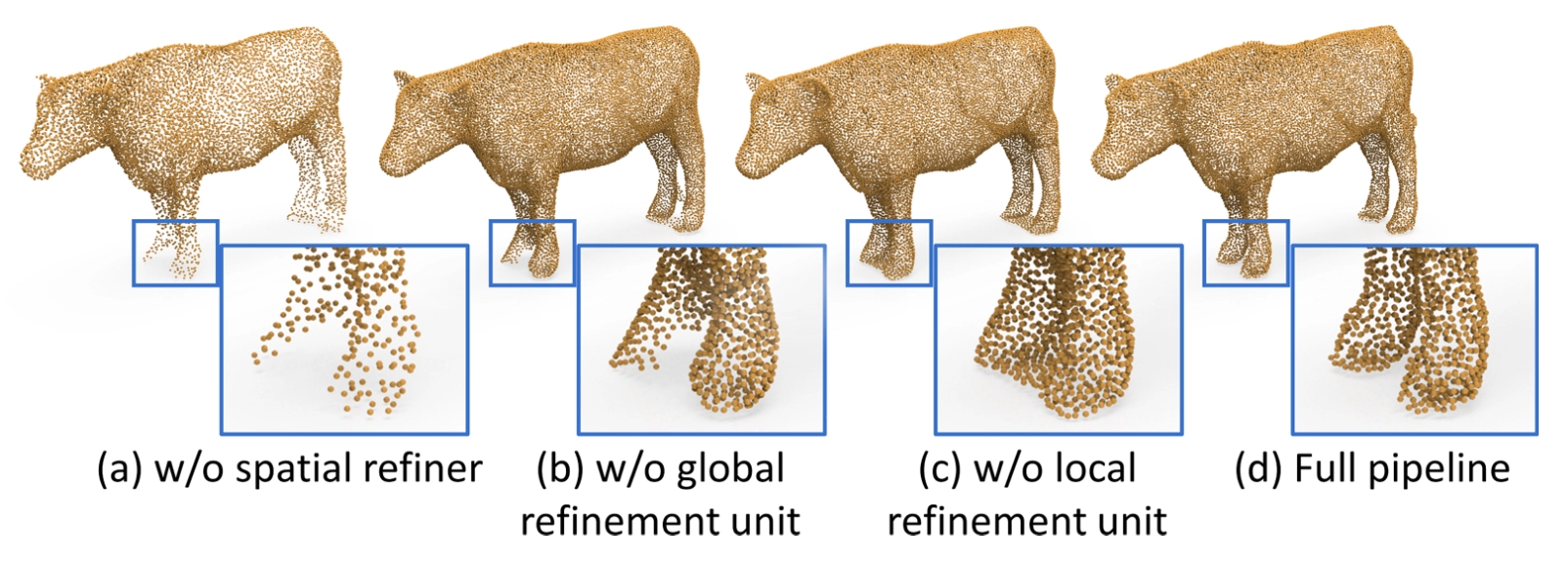
Ablation Test: Qualitative Results
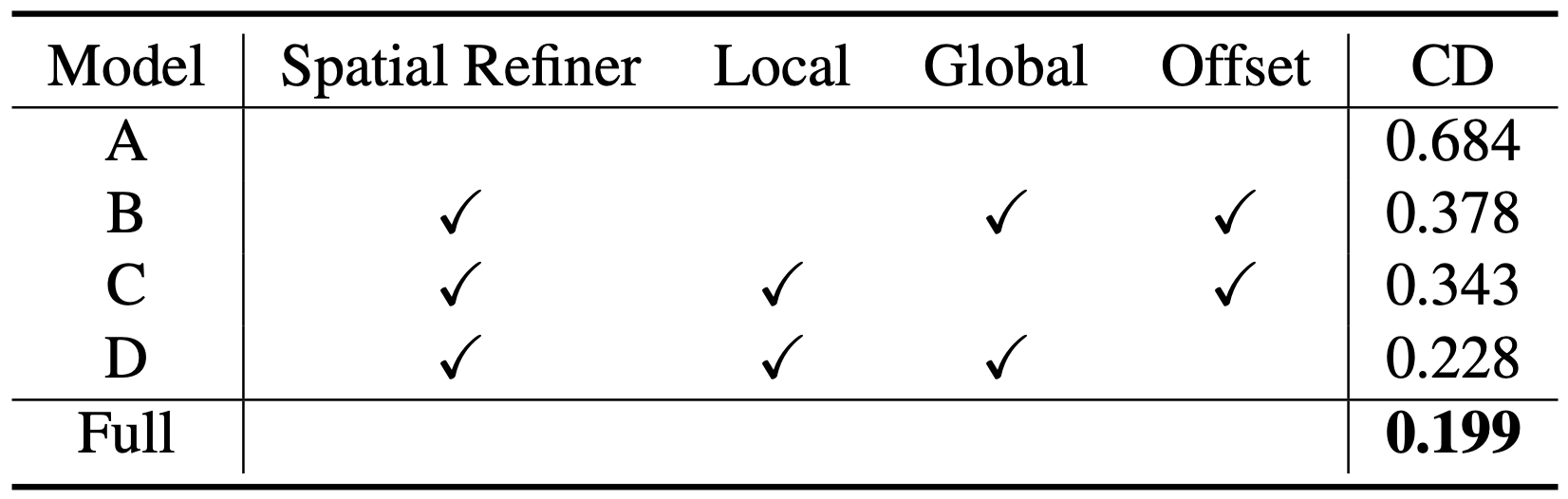
Ablation Test: Chamfer Distance
Model A 의 경우는 Spatial Refiner 자체를 없앤 경우이고, Model B, C, D 는 모두 Spatial Refiner 는 있지만 각각 Local Refinement Unit, Global Refinement Unit, 그리고 Offset Regression 을 없앤 경우입니다. Model D 같은 경우에는 Offset Regression 대신 Absolute 3D point Regression 을 사용했다고 보시면 됩니다.
정성적으로 보았을 때나 정량적으로 보았을 때나 Full Pipeline 의 경우가 가장 좋은 결과를 보여주었고, 각각의 방법론이 논문의 결과를 내는데 도움을 주었다는 사실을 알 수 있습니다. 논문에서는 언급하지는 않지만 정성적인 예시에서 제거한 방법론에 따른 생성된 point cloud 의 변화가 논문에서 의도했던 그 방법론의 동작과 일치한 형태라고 생각이 들었습니다.

Conclusion

이것으로 논문 “Point Cloud Upsampling via Disentangled Refinement” 의 내용을 간단하게 요약해보았습니다.
최근에 image super resolution 부분을 많이 다뤄서인지 Point Cloud Upsampling 이 처음보는 분야인데도 괜찮게 읽혔던 것 같습니다. 하지만, Global Refinement Unit 에 사용한 self-attention 부분에 대한 이해도가 부족하여 이 부분은 공부의 필요성이 많이 느껴졌던 것 같습니다. 전반적으로는 다른 논문에서 차용하여 가져온 구조들에 대한 구체적인 설명이 없어서 깊게 이해하기에는 시간이 많이 소요되지 않았나- 싶습니다.
이러한 부분들까지 고려하면 생각보다 논문의 난이도가 어려웠던 것 같습니다. 다만 그 만큼 얻어낸 것도 많은 것 같아 만족스러웠던 것 같습니다.