Duplicate

Lecture 21 | Depth Fusion

수강 일자
2023/03/10

Depth Map

Z=bfdZ = b\frac{f}{d}
•
일반적으로 3D 라기보다는 2.5D 정도로 불림.
•
각 픽셀은 이미지 상에서의 depth 를 의미함.
•
최근에는 얻기가 굉장히 쉬워짐. (Stereo Matching, iPhone Camera, Mono Depth)

Normal Map

•
2D 상에서 3D structure 를 표현하기 위해 depth 대신 normal 을 사용할 수도 있음.
•
각 픽셀 값별로 normal unit vector 를 대응하여 W×H×3W\times H\times3 의 크기를 가질 수도, zenith 와 azimuth 를 기준으로 W×H×2W\times H \times2 의 크기를 가질 수도 있음.
•
Depth Map 과 비교하여 Normal Map 을 사용하는 것의 장점은 카메라 거리에 무관하게 나타난다는 것임.
◦
Absolute depth 값을 찾는 것은 challenging 하고 상대적으로 normal map 을 사용하는 것은 compact 한 information 만으로 3D structure 를 표현할 수 있음.
•
Shape from shading, Photometric Stereo 등으로 얻을 수 있음.

3D Point Cloud

•
Point 의 집합으로, 딱히 순서가 주어지지 않음.
◦
순서가 없기 때문에 convolution 과 같은 네트워크를 사용하는데 무리가 있을 수 있음.
◦
Point Net 과 같은 구조가 제시되기도 했음.
•
SfM 을 통해 얻기가 굉장히 쉬움.

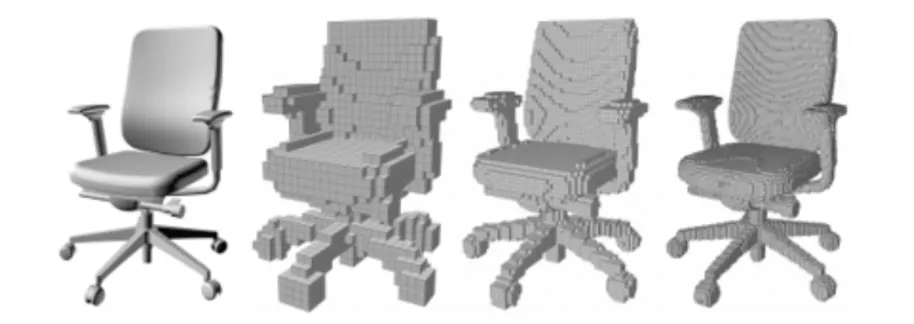
3D Voxel

•
Pixel 의 3D 버전
•
하나의 voxel 이 주어지면 주변의 voxel 이 정해지기 때문에 convolution 을 적용하기 용이함.
◦
때문에 3D convolution 을 이용하여 nerual network 분야에서 선호되는 형태임.
•
가장 큰 문제는 memory 를 너무 많이 사용한다는 점임. → O(n3)O(n^3)

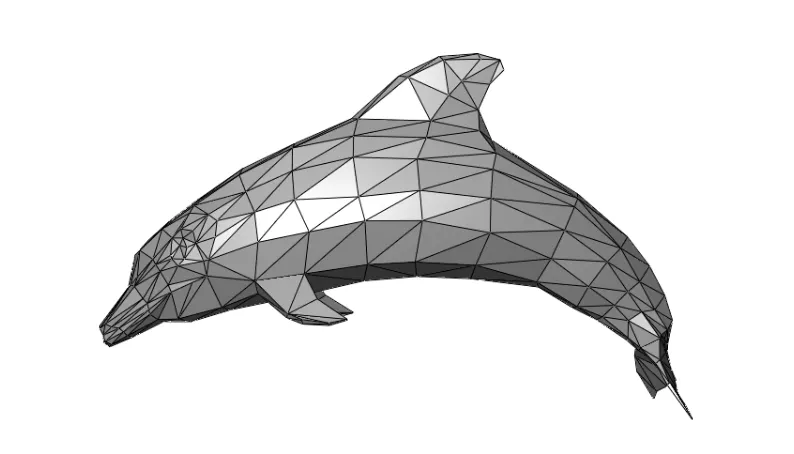
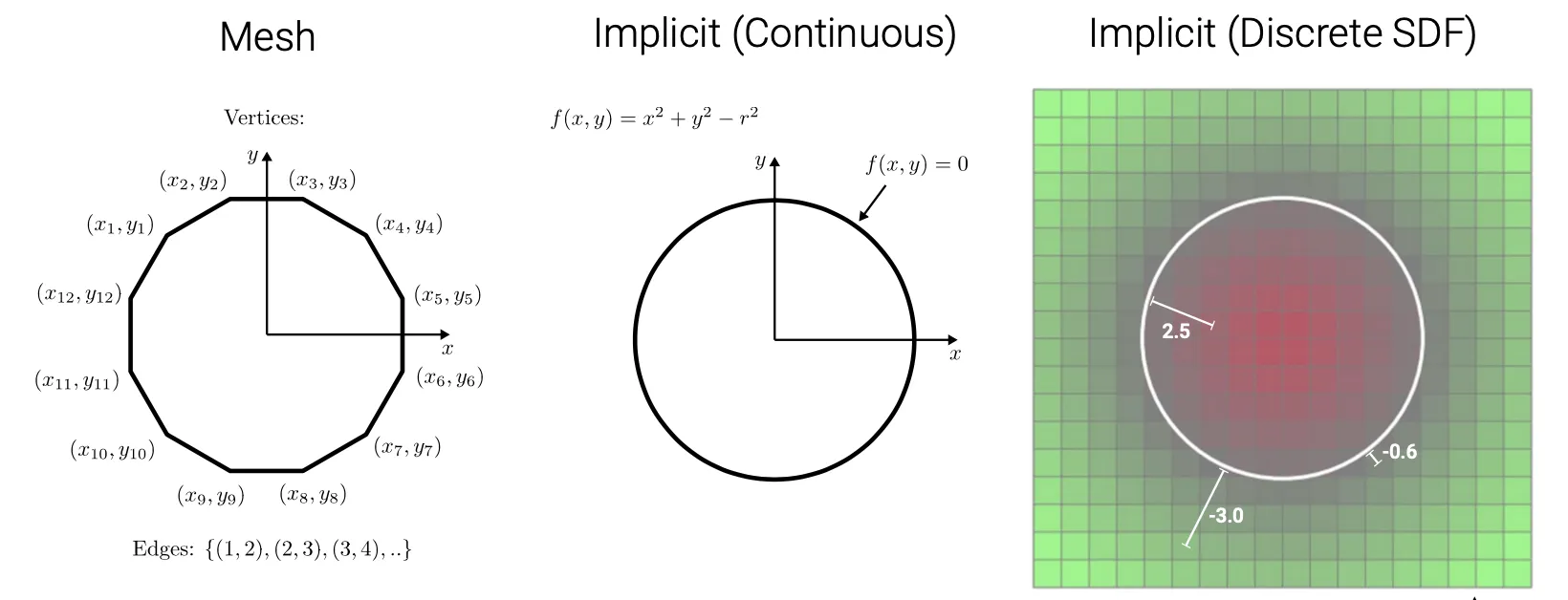
3D Mesh

•
Vertices 와 이를 이은 connection 인 faces 로 구성됨. (discritized format)
•
Surface 가 존재하기 때문에 렌더링에 이점이 있고 computer graphics 의 표준으로 활용됨.
•
각 vertex 의 위치에 변형이 일어나더라도 neighborhood 나 topology 자체가 바뀌지 않음.
◦
이는 optimization 기반의 reconstruction 에 있어서 큰 단점임.

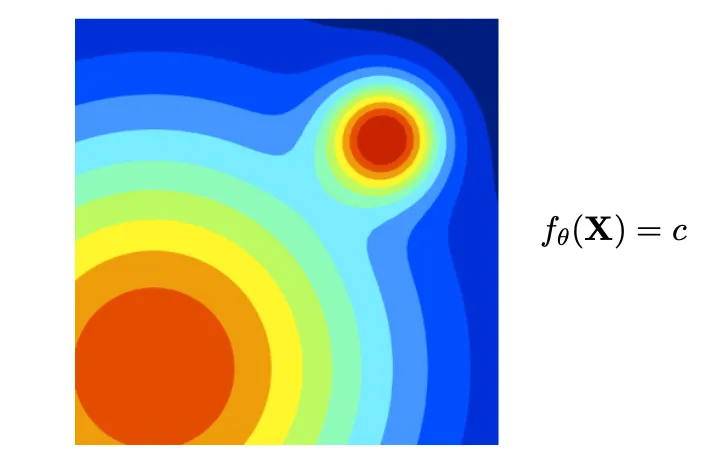
Implicit Function (Signed Distance Function)

•
Explicit 한 3D shape 가 존재하는 것이 아니라, 3D structure 의 surface 를 implicit 하게 정의하는 방법
•
Discritized 한 형태인 Mesh 나 Voxel 과는 다르게 continuous 한 surface 를 가짐.
◦
이 때문에 resolution 이나 topology 에 있어서 자유로움.
•
Occupancy filled 형태로 surface 내부를 1로 외부를 0으로 산출하는 함수를 설계하거나, surface 와의 signed distance 를 정의하는 방법이 있음.
•
단점은 explicit 하게 3D surface 를 추출해내기 위해서는 추가적인 과정이 필요함.

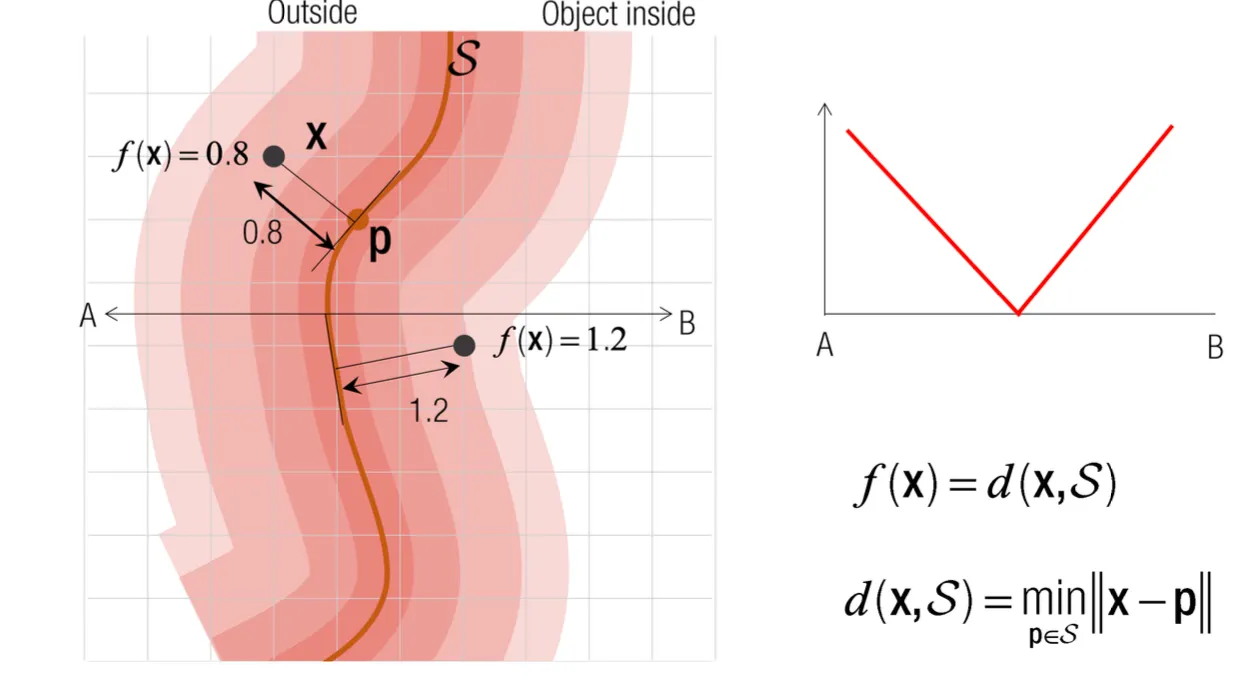
Signed Distance Function

•
가장 가까운 surface 와의 signed distance 를 각 좌표에 할당함.
◦
Surface 내부 점으로부터 surface 까지의 distance 는 양수
◦
Surface 외부 점으로부터 surface 까지의 distance 는 음수
•
Discrete 한 경우에는 discritized 된 단위별로 surface 와의 signed distance 를 할당함.
•
Explicit 하게 surface 를 재구성하기 위해서는 distance 가 0이 되는 지점을 찾아야하고, 이 과정에서 interpolation 이 필요할 수도 있음.

KinectFusion: Real-Time Dense Surface Mapping and Tracking

•
Reproduce 할 수 있는 것은 많아도 general 하게 잘 되는 알고리즘이 많지는 않은데, Kinect Fusion 은 굉장히 잘 됨.
•
Depth map → Truncated Sign Distance Function → Fuse

Distance Field & Signed Distance Field

•
Distance FIeld 는 surface 와의 거리를 나타냄.
d(x,S)=min⁡p∈S∥x−p∥d({\rm x},S) = \min_{p\in S}\|{\rm x}-{\rm p} \|
•
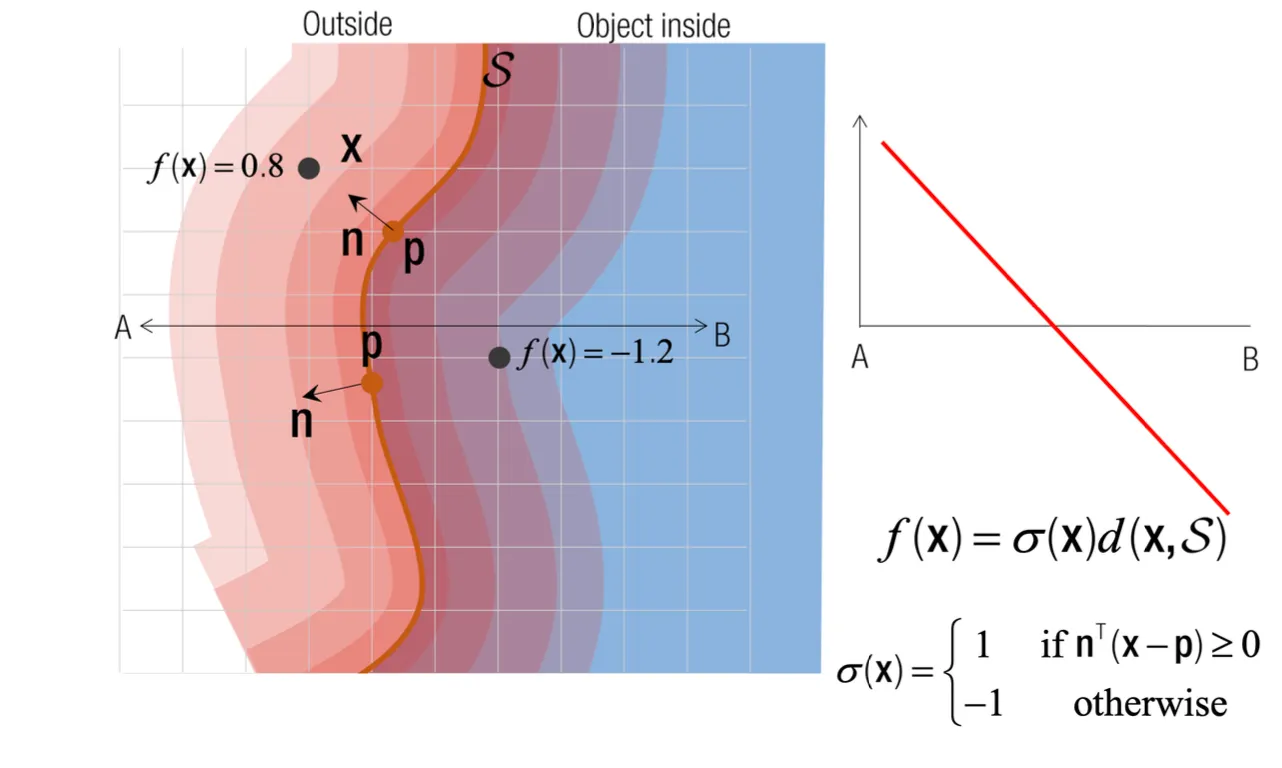
Signed Distance Field 는 surface 내부 점에서 surface 까지의 거리를 양수로, surface 외부 점에서 surface 까지의 거리를 음수로 나타냄.
f(x)=σ(x)d(x,S)σ(x)={1 if nT(x−p)≥0−1 otherwisef({\rm x}) = \sigma({\rm x})d({\rm x}, S) \\ \sigma({\rm x}) = \begin{cases} 1 \ {\rm if}\ {\rm n^T(x-p)\ge 0} \\ -1 \ {\rm otherwise} \end{cases}
◦
Distance Field 와 다르게 가지는 Signed Distance Field 의 장점은 surface (값이 0 인 지점) 가 양수인 지점과 음수인 지점 사이에 존재한다는 직관이 있다는 것임.

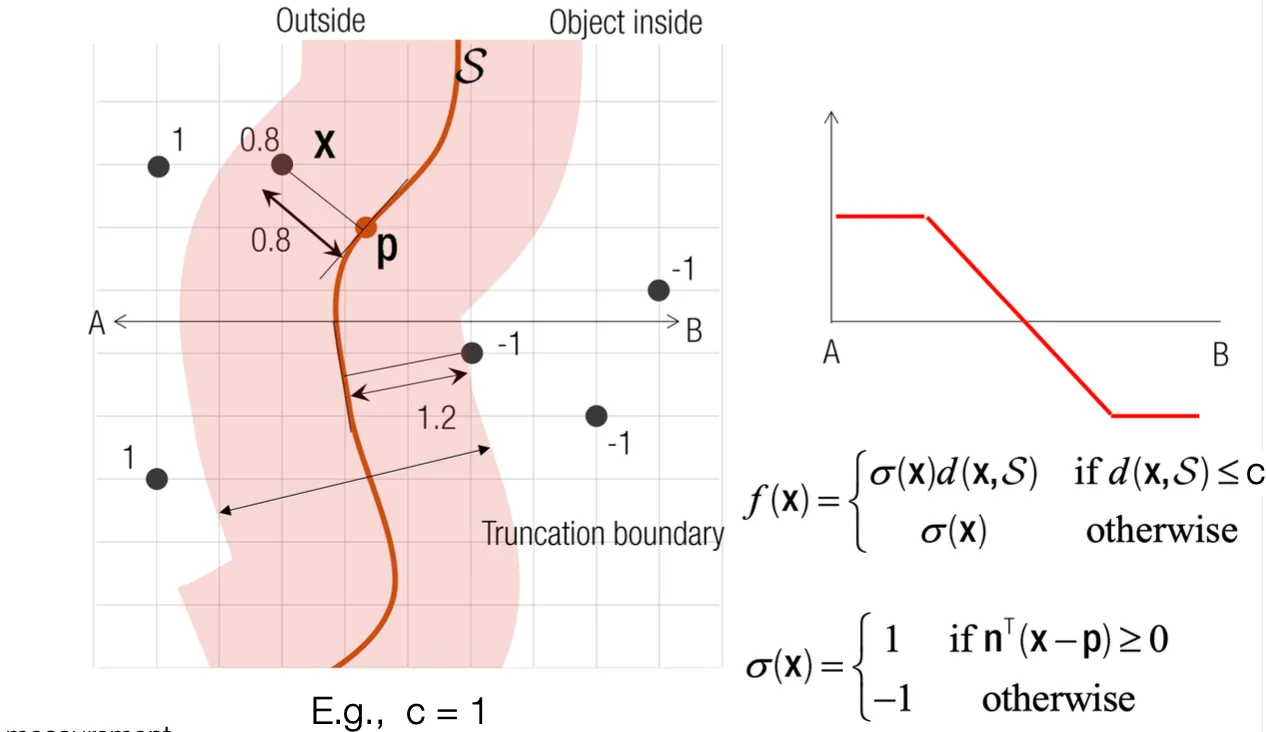
Truncated Signed Distance Field (TSDF)

•
Uncertainty 가 너무 큰, surface 로부터 거리가 먼 곳은 아예 거리를 truncated 하여 Signed Distance Field 를 정의하는 방법론

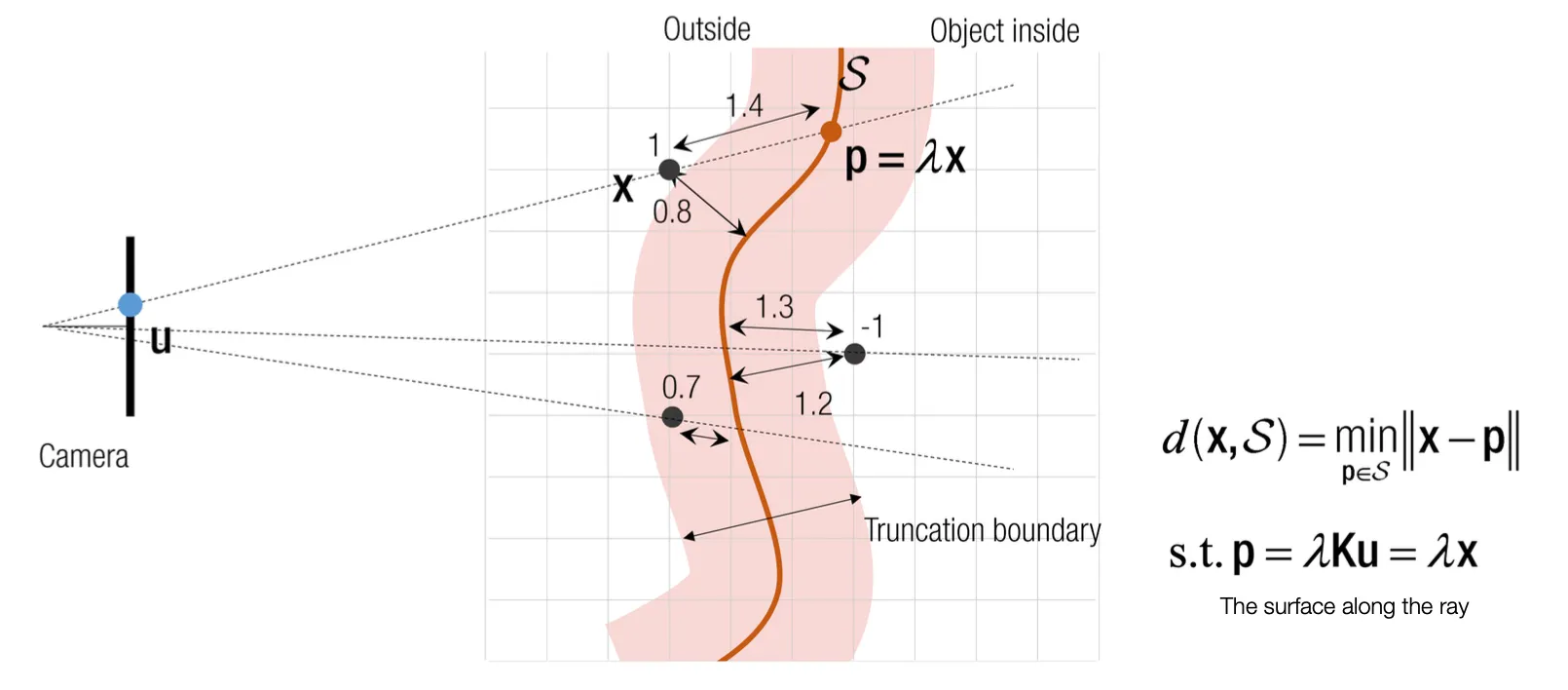
Projective TSDF

•
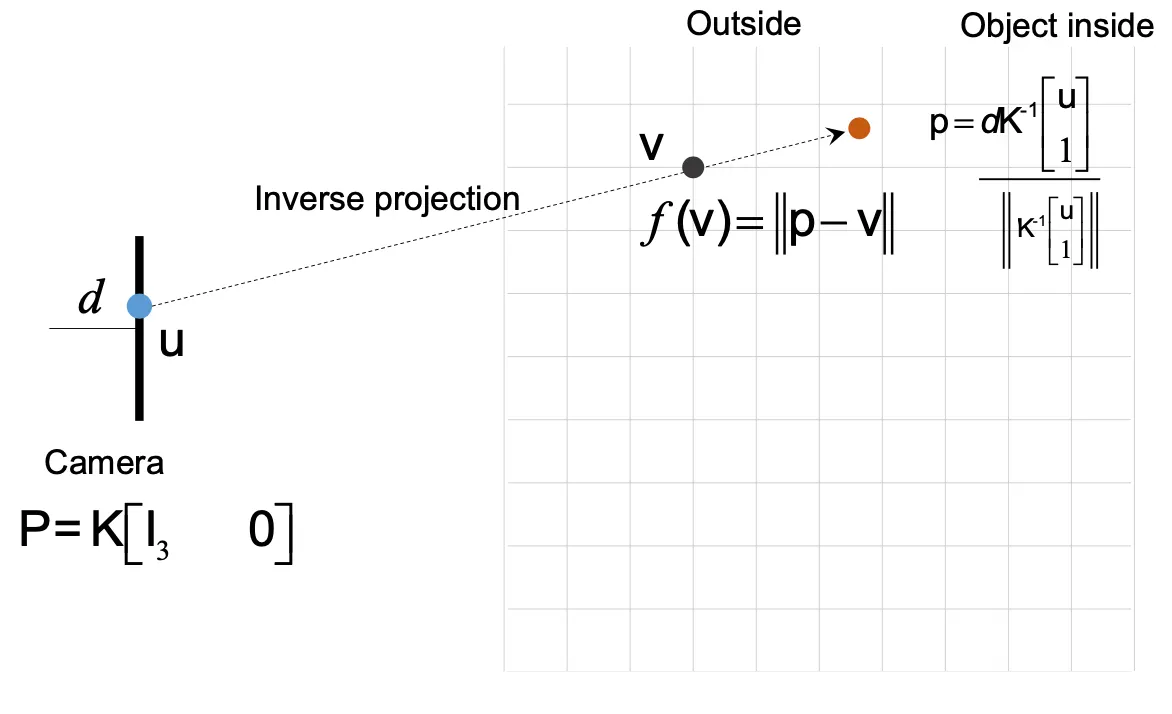
가장 가까운 점이 사실은 정확한 distance 이지만, 이것을 알 길이 없기 때문에, ray 기반의 depth 로 distance 를 approximate 하는 방법론

Constructing TSDF from Depth

•
Inverse Projection 을 통해 ray 의 식을 구하고, 해당 식과 depth 를 결합하여 실제 ray 위에 존재하는 점 중 object 위의 point 위치를 찾을 수 있음.
◦
이를 이용해서 ray 위의 모든 점에 대해 Projective TSDF 를 구할 수 있음.
•
Point Cloud 를 구성하는 방법이기도 함.

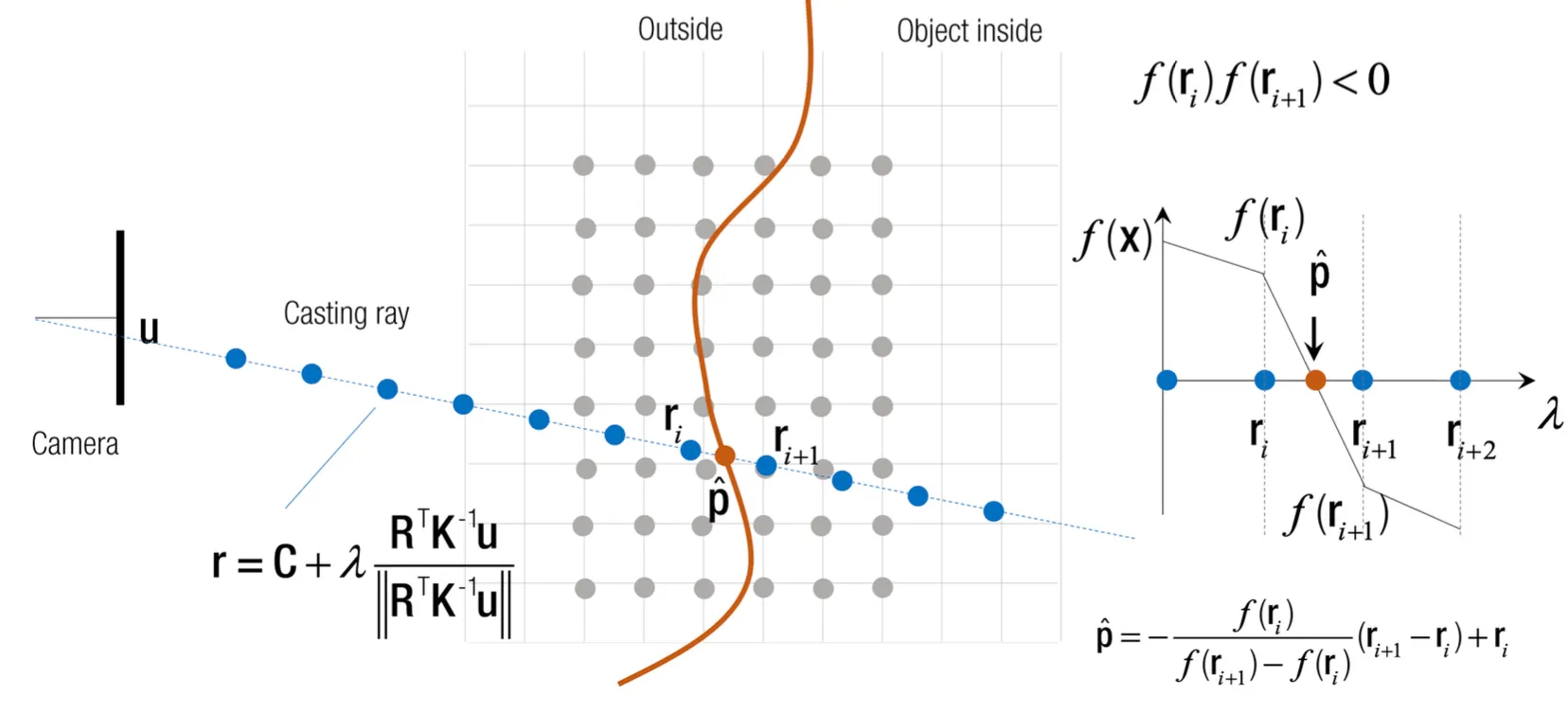
Surface Reconstruction from TSDF

•
각 ray 상에서 점을 sampling 하여 sampling 된 점마다 Truncated TSDF 값을 구할 수 있고, 해당 값이 양수에서 음수 등으로 부호가 바뀌는 지점에서 interpolation 을 하면 ray 상에서 Truncated TSDF 0 값을 가지는 surface 위치를 구할 수 있음.
•
Surface Normal 같은 경우에는 point 주변의 plane 의 vectior 의 cross product 로 구해냄

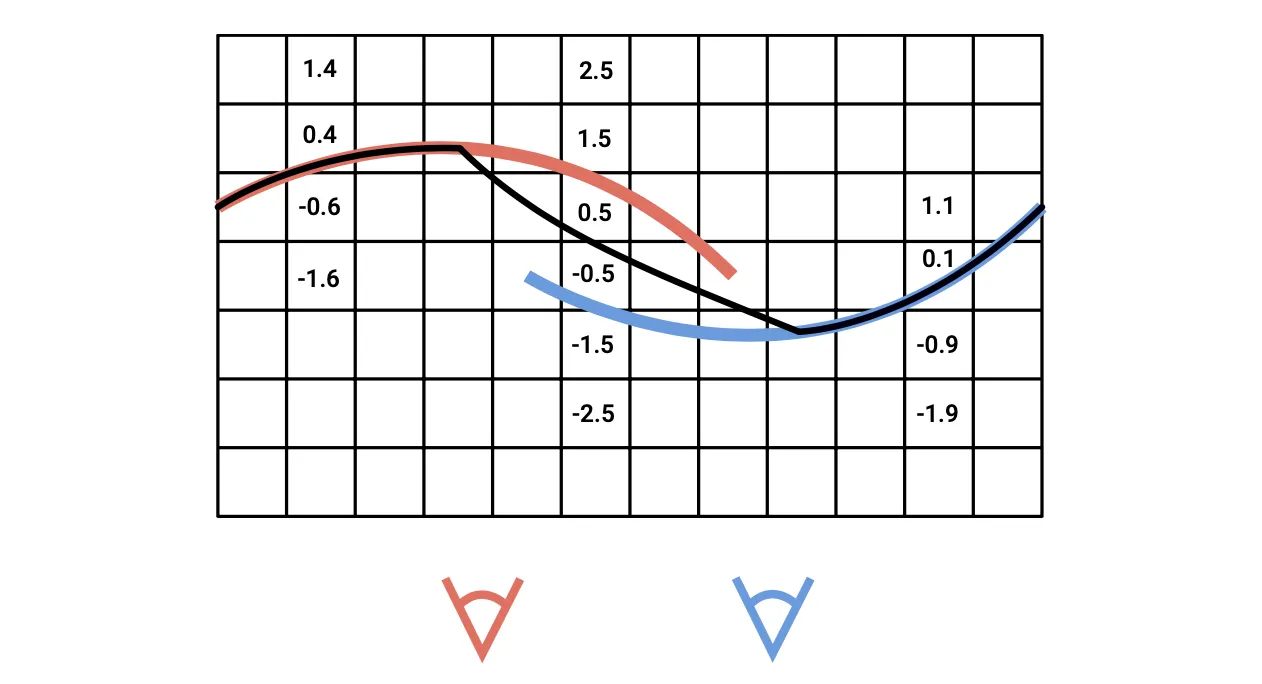
Volumetric Fusion

•
여러 depth map 으로부터 얻어진 Signed Distance Field 를 융합학 위해서 그냥 겹치는 부분의 Signed Distance 를 average 하는 것임.
•
실제로는 더 fancy 한 방법을 위해 weighted average 를 할 수도 있음.
D(x)=∑iwi(x)di(x)∑iwi(x)W(x)=∑iwi(x)D({\rm x}) = \frac{\sum_i w_i({\rm x})d_i({\rm x})}{\sum_i w_i(\rm x)} \quad W({\rm x}) = \sum_i w_i({\rm x})
•
새로운 measurement 가 들어올 때 incremental 하게 값을 update 하는 방법도 있음.

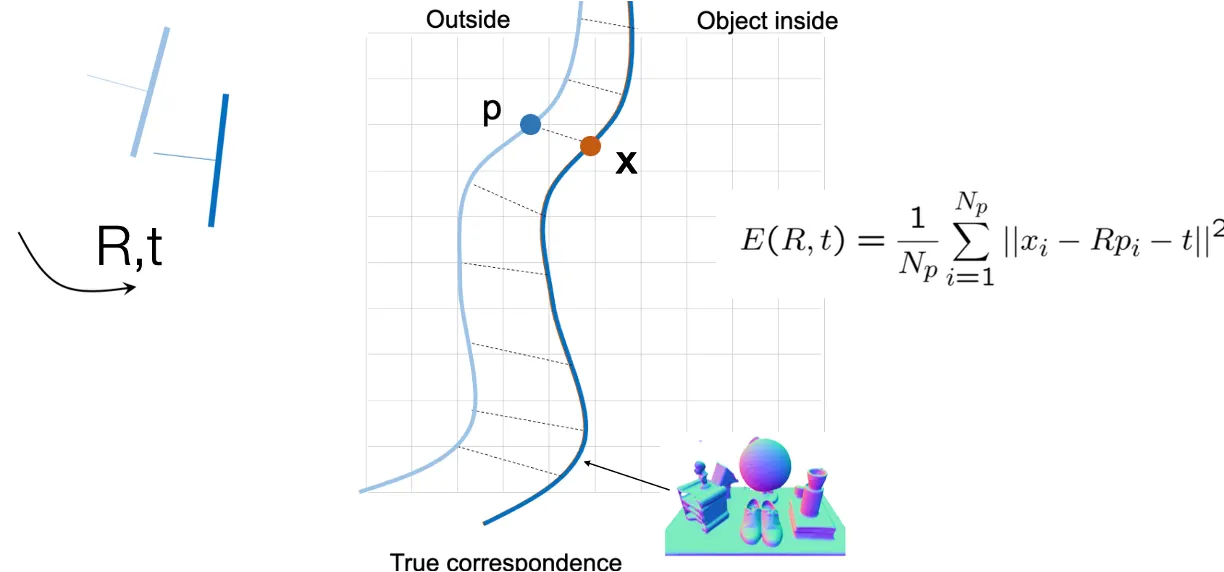
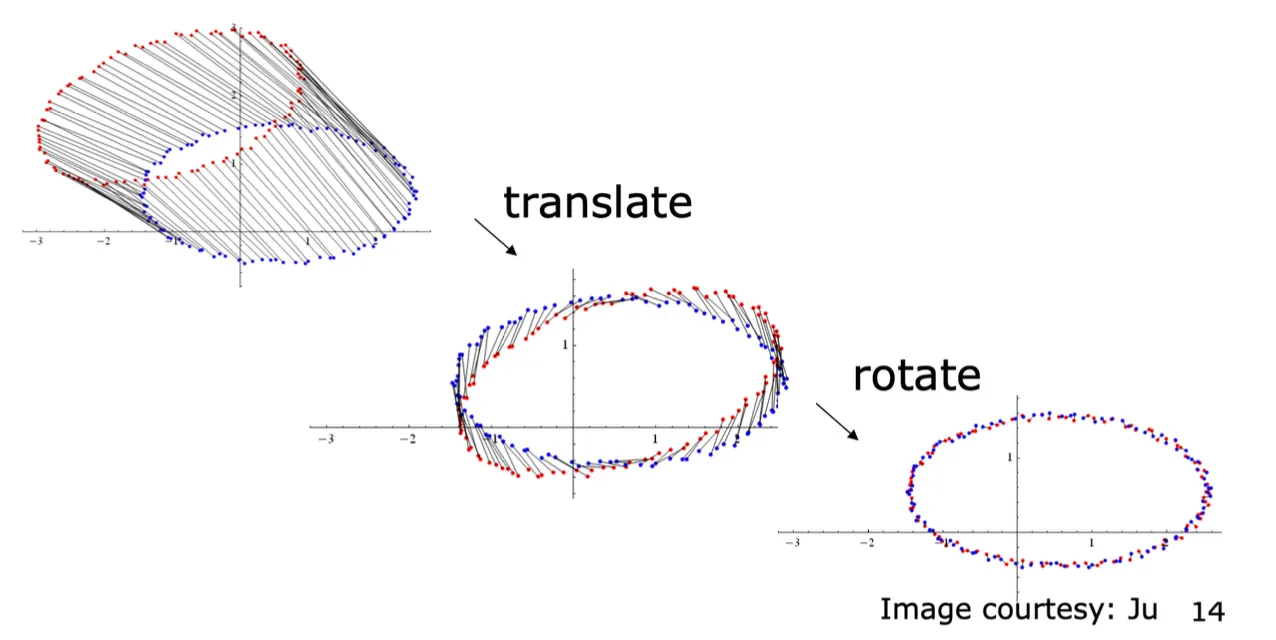
Point Cloud AI (ICP Algorithm)

•
기존의 surface 와 달라진 calibratio 상에서 달라진 surface 의 차이를 이용해 calibration R,tR,{\rm t} 를 구하는 과정
•
Corresponding Point 를 closest point 로 지정하고 iterative 하게 변환을 적용하거나, ㅜon-linear optimization 을 하면 두 surface 를 붙게 할 수 있는 R,tR, {\rm t} 를 구할 수 있음.
◦
다만, corresponding point 가 정확하게 주어지면, closed form 으로 이 값을 구할 수도 있음.

SVD-Based Alignment Summary

•
Corresponding point 가 정확하게 주어지면, closed form 으로 R,tR, {\rm t} 를 구하는 방법론
•
Center of Mass 를 먼저 변환하여 Translation 을 구하고, rotation 성분만 구하면 됨.
◦
Cross-covariance Matrix 를 구하고 SVD 로 UΣVTU\Sigma V^T 를 구한 뒤 R=UVTR=UV^T 로 해버릴 수 있음.
◦
Translation 은 rotation 성분을 곱한 뒤 기존에서 빼서 구할 수 있음.

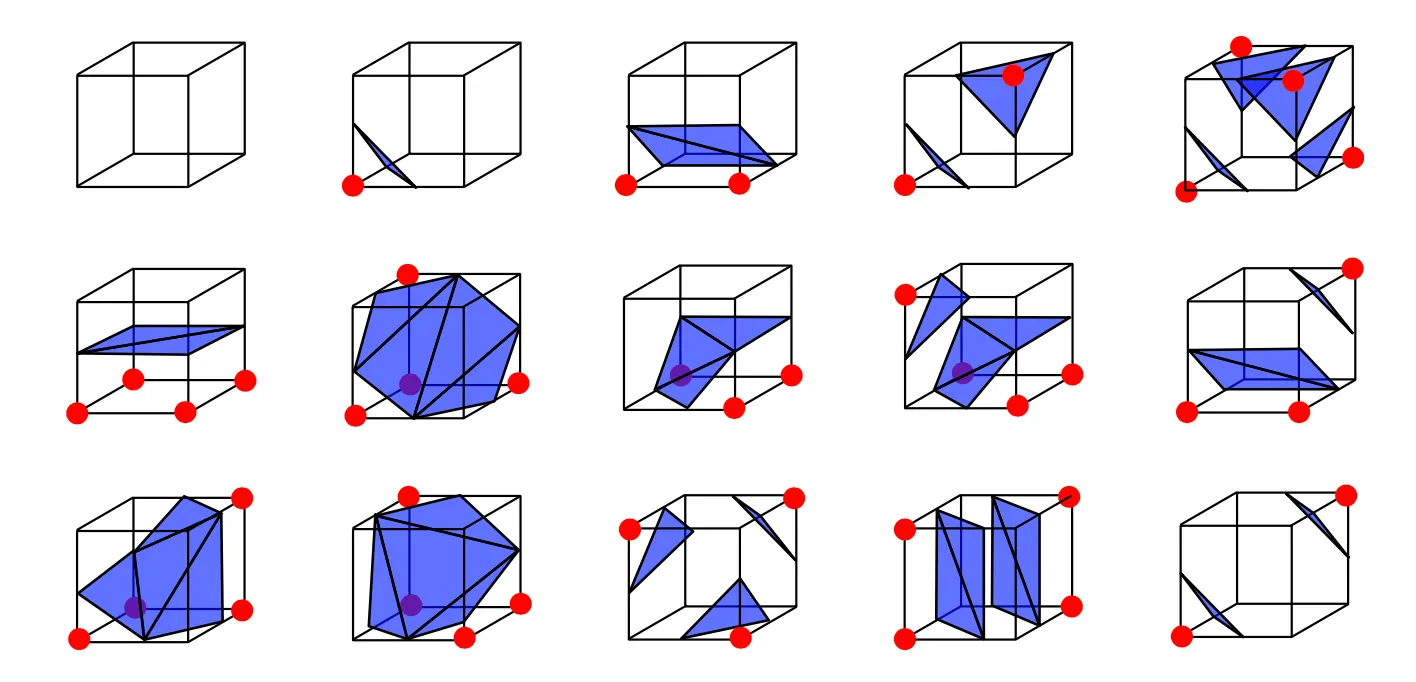
Marching Cube

•
Voxel grid 상에서 TSDF 가 양수, 음수인 조합의 개수가 정해져 있고, 이에 따른 surface 의 형태가 고정되어 있음. (Look-Up-Table)
•
Iterative 하게 해당 Cube 를 template matching 하듯이 돌려보고 어떤 양/음 의 형태를 가지는지에 따라서 surface 의 대략적인 모습을 그려낼 수 있게 됨.

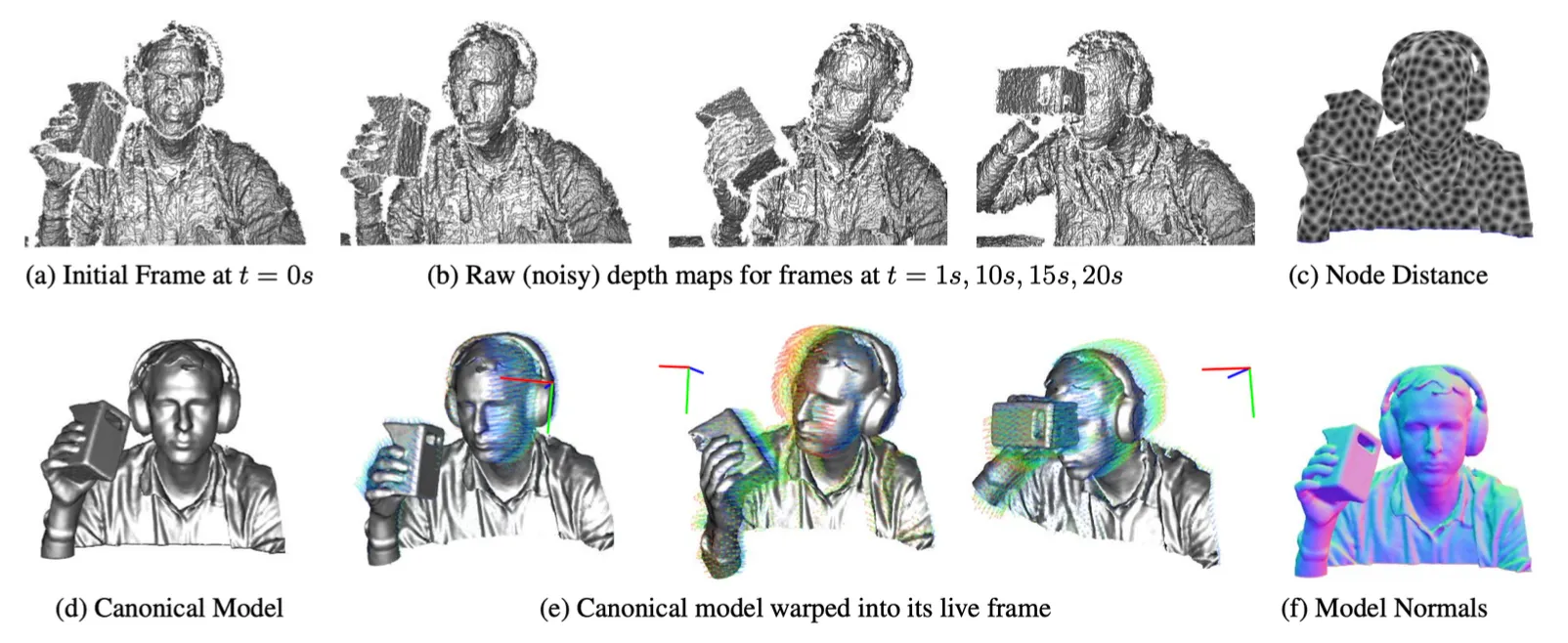
DynamicFusion

•
SfM 과 KinectFusion 의 동일한 문제점은 target 이 static 해야 한다는 점임.
•
바뀐 measurement 를 warping 결과에 어떻게 합쳐줄까에 대한 문제임.
•
Practical 하게 잘 되지는 않음.