Duplicate

Lecture 4 | Image Sampling and Pyramid

수강 일자
2022/09/20

Image Scaling (Resize)

•
Image Processing 중 가장 많이 하는 것이 resizing 임.
•
원본 해상도(ex. 1920×20801920\times2080) 보다 작은 화면 (ex. 720×1080720\times 1080) 에서 보게 될 경우 자동으로 resize 를 하게 됨.

Image Sub-Sampling

•
이미지를 반으로 줄이고 싶을 때는 번갈아가면서 한 Row, Column 씩 버리면 됨.
•
Row, Column 을 버리는 형태로 resizing 을 하면 본래 사이즈로 zoom 했을 때 shape 이 망가지거나, noisy 해지는 여러가지 artifact 가 생김.

Good and Bad Sampling

•
첫 번째 행의 Sampling 들은 검검흰흰검검흰흰 / 검흰검흰 등으로 검흰이 같은 개수로 반복되고 이는 원본에서 나타난 패턴과 동일한 형태이기 때문에 좋은 Sampling 임. → 원본의 패턴을 유지하는 좋은 Sampling 을 위해서는 많은 수의 Sample 을 두거나 잘 Sampling 을 해야함!
•
두 번째 행의 Sampling 은 검검검검 / 검흰흰 등으로 아예 원본 패턴을 잃어버리거나 원본패턴이 왜곡되어 나타는 형태이기 때문에 나쁜 Sampling 임. → Aliasing 이라고 함.

Aliasing (Examples)

•
Wave 예시: 본 Signal 보다 현저하게 낮은 frequency 로 Sampling 하게 될 경우 원본의 패턴을 잃어버림
•
Wagon-Wheel Effect: 자동차 바퀴의 회전속도에 비해서 비디오의 FPS 가 작을 때 간혹 자동차 바퀴가 반대로 굴러가는 것처럼 보이는 현상. (30 FPS 의 영상인데 실제 바퀴가 1바퀴 도는데 1/30 초보다 조금 더 걸릴 경우)
•
Stroboscopic Effect: 침이 시계방향으로 도는데 한 바퀴 도는데 걸리는 시간만큼의 간격으로 Sampling 을 하면 침이 움직이지 않는 것처럼 보이거나 한 바퀴 도는데 걸리는 시간보다 살짝 짧게 Sampling 을 하면 침이 반대방향으로 움직이는 것처럼 보이는 현상.
•
헬리콥터의 날개가 멈춰있는데 뜨는 현상, 헬리콥터의 날개가 반대로 도는 현 상도 있음.

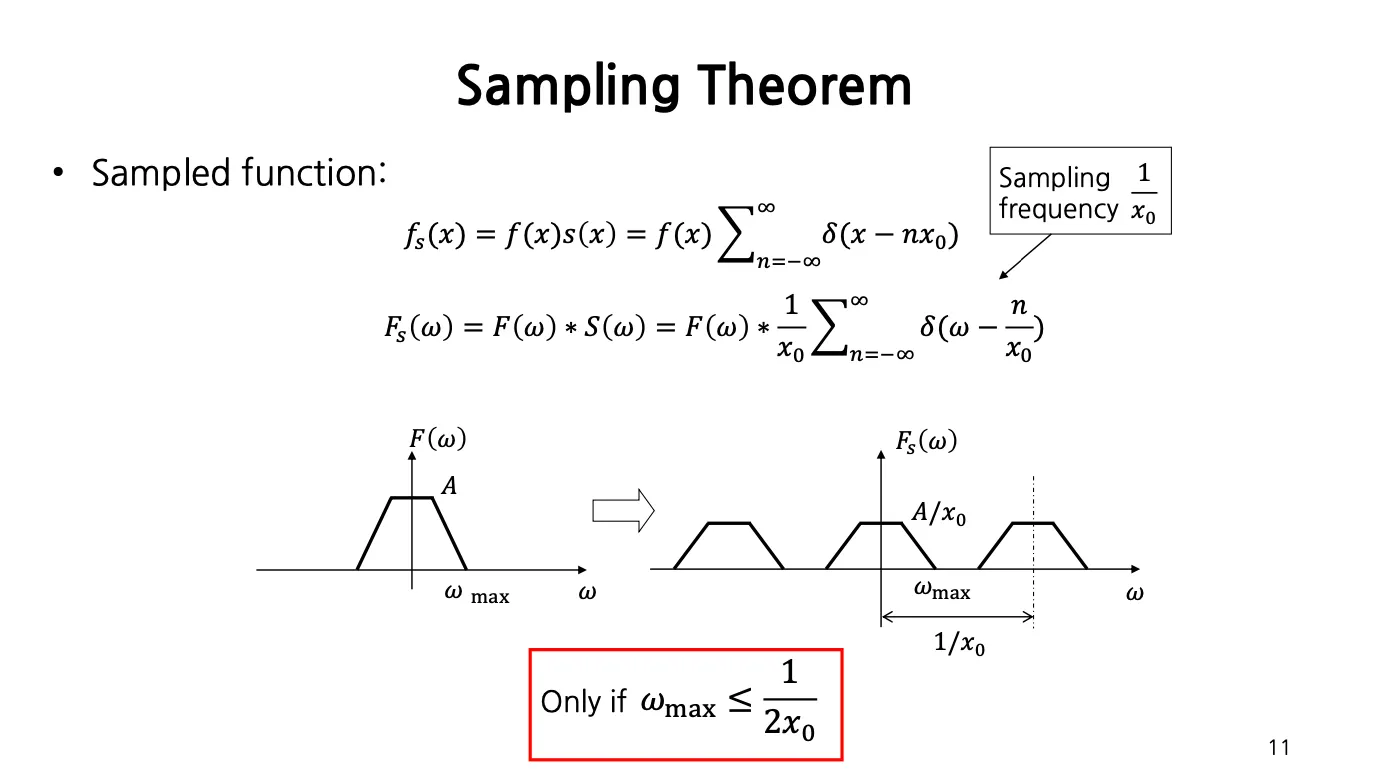
Sampling Theorem

•
Shah function (Impulse Train)
s(x)=∑m=∞∞δ(x−nx0)s(x)=\sum_{m=\infty}^\infty \delta(x-nx_0)
◦
x0x_0 는 impulse 간의 간격을 의미
•
원본 continous signal 과 shah function 과의 곱이 sampling 된 function 을 의미함.
fs(x)=f(x)s(x)=f(x)∑m=∞∞δ(x−nx0)f_s(x)=f(x)s(x)=f(x)\sum_{m=\infty}^\infty \delta(x-nx_0)
◦
위 Sampled function 을 fourier transform 을 사용하여 frequency domain 으로 바꿀 수 있음.
Fs(ω)=F(ω)∗S(ω)=F(ω)∗1x0∑n=∞∞δ(ω−nx0)F_s(\omega)=F(\omega)*S(\omega) = F(\omega)*\frac{1}{x_0}\sum_{n=\infty}^\infty \delta(\omega-\frac{n}{x_0})
◦
원본 signal 의 가장 큰 frequency 를 ωmax⁡\omega_{\max} 라고 할 때 위 Fs(ω)F_s(\omega) 는 ωmax⁡\omega_{\max} 가 12x0\frac{1}{2x_0} 보다 작을 경우에 한해서 signal 을 1x0\frac{1}{x_0} 간격으로 복사하게 됨.
◦
ωmax⁡>12x0\omega_{\max} > \frac{1}{2x_0} 일 경우에는 signal 이 겹쳐지게 되고, 이 경우가 aliasing 이 일어나는 상황임.
◦
Fs(ω)F_s(\omega) 로부터 F(ω)F(\omega) 를 복원할 수 있으려면은 ωmax⁡≤12x0\omega_{\max} \le\frac{1}{2x_0} 을 만족해야 하고 등호조건일 때의 frequency 를 Nyquist Frequency 라고 함. → 한 주기당 적어도 2개의 sample 이 필요

Sub-Sampling with Gaussian Pre-Filtering

•
한 주기당 적어도 2개의 Sample 이 필요한데, 34\frac{3}{4} 이상을 날려야 하는 resizing 에서 aliasing 이 없도록 하려면 원본 이미지의 max frequency 를 낮추어서 주기를 길게 만들어 필요 sample 수를 줄여야 함.
•
원본 이미지를 low-pass filter 인 gaussin filter 를 거친 후 sub-sampling 을 할 수 있음.
•
위 그림에서 좌(Gaussian + Sub-Sampling) / 우 (Sub-Sampling)
◦
Gaussian Smoothing 을 사용해서 detail 은 사라지지만 적어도 aliasing 으로 인한 이상한 패턴이 생기지는 않음 (no artifact)

Multi-Resolution Image Pyradmids

•
주어진 사진의 14\frac{1}{4}, 116\frac{1}{16}, 164\frac{1}{64} 등 낮은 해상도로 여러 개의 사진을 가지고 있는 것을 Multi-Resolution Image Pyramid 라고 함.
◦
사람의 뇌에서 시각 정보를 가지고 있을 때에도 여러 개의 resolution 으로 가지고 있음.
◦
연산에 효과적임.
▪
일반적으로 어딘가에 사진을 업로드할 때, 낮은 해상도의 버전도 같이 만들어서 가지고 있은 뒤에 스마트폰으로 보면 낮은 resolution 의 이미지를 로딩하고, 컴퓨터 모니터로 보면 높은 resolution 의 이미지를 로딩해줌.
▪
높은 resolution 의 사진을 전송하는게 네트워크 측면에서 좋지 못한 경우가 종종 있음.
•
Pyramid 를 저장하는데 가지고 있어야 하는 메모리
N2+(12N)2+(14N)2+...=43N2N^2 + (\frac{1}{2}N)^2+(\frac{1}{4}N)^2+...=\frac{4}{3}N^2
◦
기존 고해상도의 이미지 하나만 가지고 있을 때보다 43\frac{4}{3} 배 정도밖에 더 필요하지 않기에 메모리의 큰 낭비가 아님.
•
Pyramid 를 구성할 때도 Sub-Sampling 이 필요하기 때문에 일반적으로 aliasing 이 나타남.

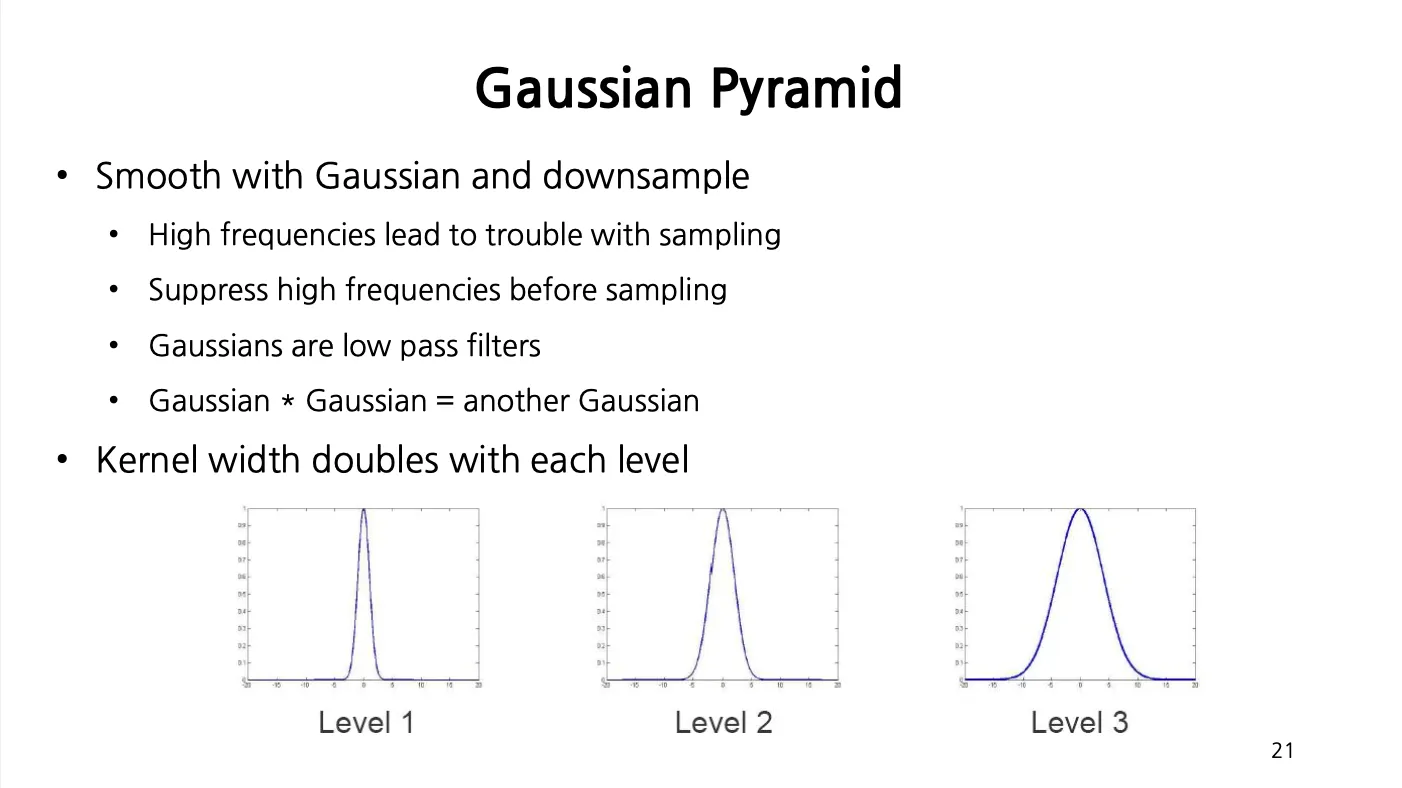
Gaussian Pyramid

•
원본 이미지를 downsampling 할 때, Gaussian Filter 를 적용하여 high frequency term 을 없애서 aliasing 을 예방한 형태로 생성한 Pyramid.
•
Gaussian 을 convolve 한 이미지에 또 다시 Gaussian 을 convolve 하면 이는 다른 Gaussian 하나를 convolve 한 것과 동일함.
•
Level 이 증가할때마다 하나의 차원에서 픽셀의 수가 반으로 줄고, 이에 따라 Sampling Frequency 가 반으로 줄어듬. 이에 따라 Gaussian Kernel 의 width 는 2배가 되어야 함.

Laplace of Gaussian (LoG)

•
Laplacian of an image
L(x,y)=∂2I∂x2+∂2I∂y2L(x,y)=\frac{\partial^2 I}{\partial x^2} + \frac{\partial^2 I}{\partial y^2}
◦
I(x,y)I(x,y): 원본 이미지의 (x,y)(x,y) 좌표의 intensity
◦
Edge Detection 에 유용하게 사용됨.
◦
Interest Point Detection (특징점 찾기) 에 유용하게 사용됨.
•
Laplacian 의 문제점은 2차 미분 항 때문에 noise 에 sensitive 하다는 점
◦
Gaussian 을 거친 후 Laplacian 을 적용하는 형태로 어느정도 해소할 수 있음.
◦
편미분을 해야하기 떄문에 연산이 복잡함 → 효율적으로 값을 근사하여 얻는 방법 활용 가능

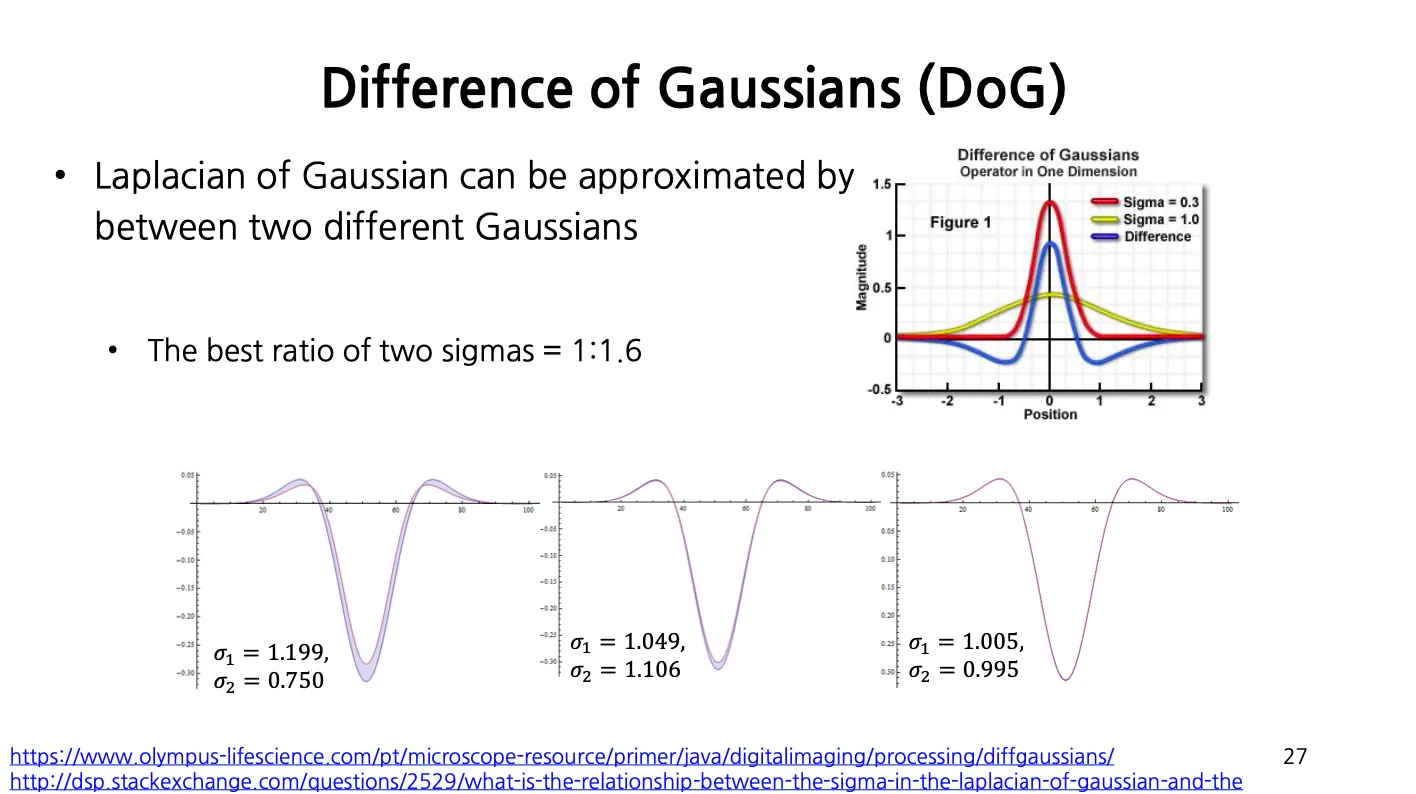
Difference of Gaussian (DoG)

•
Laplace of Gaussian 의 연산 복잡도 때문에 근사하여 효율적으로 얻는 방법론임.
•
σ\sigma 가 다른 두 Gaussian 의 차이를 이용해서 Laplacian of Gaussian 을 근사함.
◦
두 sigma 의 비율을 1:1.6 정도로 설정하면 Laplacian of Gaussian 과 Difference of Gaussian 이 굉장히 비슷한 것을 알 수 있음.

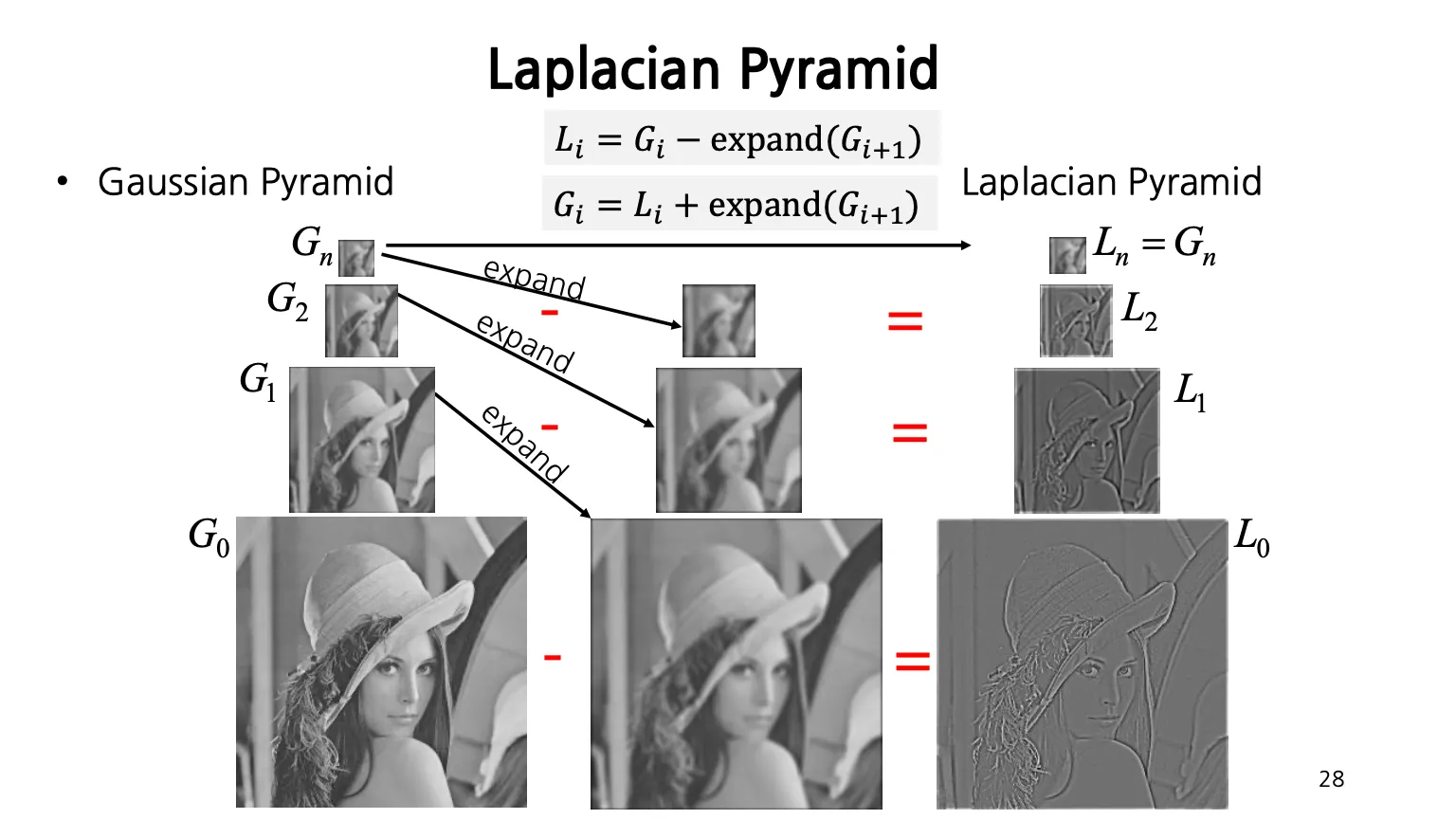
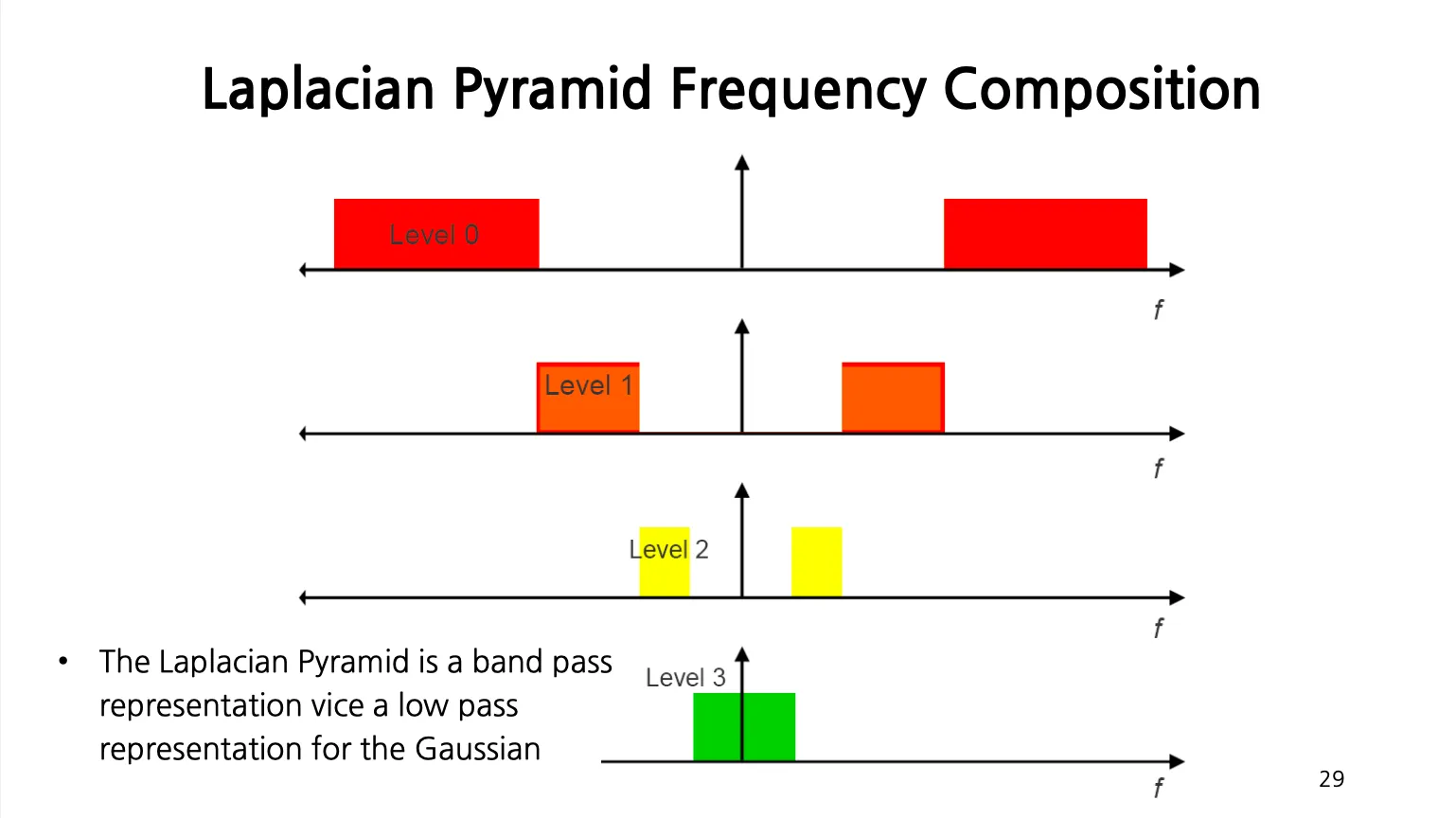
Laplacian Pyramid

•
Laplacian Pyramid 는 Gaussian Filter 를 쓰는 과정에서 high frequency term 을 잃어버리는 것이 상당히 lossy 한 과정이기 때문에, 이렇게 정보를 잃는 과정이 없이 Pyramid 를 만들 수 있지 않을까- 하여 탄생한 Pyramid 임.
•
Gaussian Filter 를 거쳐서 나온 이미지와 원래 이미지의 차이인 residual 은 보통 edge 를 강조하는 형태의 이미지인데, 이를 보관하는 아이디어임.
•
Laplacian Pyramid 를 만들 때, 원본 이미지에 Gaussian Filter 를 적용하고 차를 구한 것이 DoG 가 되서 Pyramid Level 0 으로 사용함. Resizing 하여 동일한 과정을 거쳐 Level 1, … 을 만든 후 마지막 Level 은 아무 처리 없이 그대로 Level N 으로 사용함.
◦
이미지를 확장한 뒤에 Laplace Pyramid 를 더해주면 원본 복원이 가능!
•
마지막 Level 은 제외하고 Gaussian 을 거친 것을 뺀 것이 Pyramid 의 Level 로 사용되기 때문에 band pass representation 이자 gaussian 의 low pass representation 임.

Applications of Image Pyramid

•
Fast Template Matching
◦
Template Matching 을 할 때 낮은 resolution 에서 먼저 matching 하고 fine 하게 바꿈으로써 computational efficiency 를 챙김.
◦
Template Matching 시 m×nm\times n Image 와 p×qp \times q Template 에 대해서 O(mnpq)O(mnpq)
◦
Template 과 Image 모두 Image Pyramid 를 만듬.
◦
작은 크기의 Template 과 Image 에서 Template Matching 을 수행한 뒤, Strong Match 가 보였던 곳 근처를 큰 크기의 Template 과 Image 에서 집중적으로 탐색하는 것을 점점 더 고해상도 이미지에서 반복함.
◦
Strong Match 를 찾기 위해 threshold 를 설정할 텐데, threshold 가 너무 작으면 후보 영역이 많아 Computational Cost 가 클 것이고, 너무 크다면 miss match 가 발생할 수 있음.
◦
31 초 걸리는 기존 Template Matching 을 Image Pyramid 를 활용하여 0.5 초에 수행할 수 있음.
•
Image Blending
◦
두 개의 Image 를 blend 할 때 Laplacian Pyramid 를 쓸 수 있음.
◦
두 이미지 A, B 의 Laplacian Pyramid LAL_A, LBL_B 로, 겹쳐지는 부근의 영역 RR 의 Gaussian Pyramid 를 GRG_R 이라 할 때, 최종적인 겹쳐지는 영역의 Blended Image 의 Laplacian Pyramid 는 다음과 같이 정의됨.
Ls(i,j)=GR(i,j)⋅LA(i,j)+(1−GR(i,j))⋅LB(i,j)L_s(i,j)=G_R(i,j)\cdot L_A(i,j)+(1-G_R(i,j))\cdot L_B(i,j)
◦
겹쳐지지 않는 영역은 좌측이면 LAL_A 로, 우측이며 LBL_B 로 그대로 사용해서 만들어냄.
◦
위에서 구한 LsL_s 의 모든 Level 을 확대해서 Laplacian 을 더하는 과정을 반복하여 최종 Blended Image 를 얻을 수 있음.
•
직접 다루지는 않지만 Data Compression 에서도 많이 활용됨.
•
SIFT Feature Extraction 에서도 활용.