Duplicate

Lecture 2 | Image Processing

수강 일자
2022/09/06

Image as Function

•
Image 를 2 차원의 coordinate 에서 1 차원의 intensity 로 매칭되는 하나의 function
f:R2→Rf: \mathbb{R}^2 \rarr \mathbb{R}
•
Colorized Image 은 2차원의 coordinate 에서 3차원의 RGB intensity 로 매핑되는 function
f:R2→R3f: \mathbb{R}^2 \rarr \mathbb{R}^3
•
Image 를 하나의 함수로 치면 Image Processing 은 함수 ff 를 함수 gg 로 변경함에 있어 적용하는 transformation 인 TT 를 의미함.
g=T(f)g=T(f)
•
이러한 TT 로 어떠한 것들이 가능한지 알아볼 예정

Point Operations

•
M×NM\times N Image 를 같은 크기의 새로운 M×NM\times N Image 로 변환하는데 변환 전 i×ji\times j 에 있는 픽셀의 정보만이 변환 후 같은 위치인 i×ji \times j 에 있는 픽셀에 영향을 줄 수 있는 Image Processing 방법론을 Point Operation 이라고 함.
•
Invert
g(x,y)=255−f(x,y)g(x,y)= 255-f(x,y)
•
Darken
g(x,y)=f(x,y)−128g(x,y)=f(x,y)-128
•
Lighten
g(x,y)=f(x,y)+128g(x,y) = f(x,y) + 128
•
Lower Contrast
g(x,y)=f(x,y)/2g(x,y)=f(x,y)/2
•
Raise Contrast
g(x,y)=f(x,y)×2g(x,y) = f(x,y) \times 2
•
Nonlinear Lower Contrast
g(x,y)=(f(x,y)/255)0.33×255g(x,y)=(f(x,y)/255)^{0.33}\times 255
•
Nonlinear Raise Contrast
g(x,y)=(f(x,y)/255)2×255g(x,y)=(f(x,y)/255)^2 \times 255

Neighborhood Operations

•
M×NM\times N Image 를 같은 크기의 새로운 M×NM\times N Image 로 변환하는데 변환 전 i×ji\times j 에 있는 픽셀 근처의 픽셀 정보만이 변환 후 같은 위치인 i×ji \times j 에 있는 픽셀에 영향을 줄 수 있는 Image Processing 방법론을 Neighborhood Operations 라고 함.
•
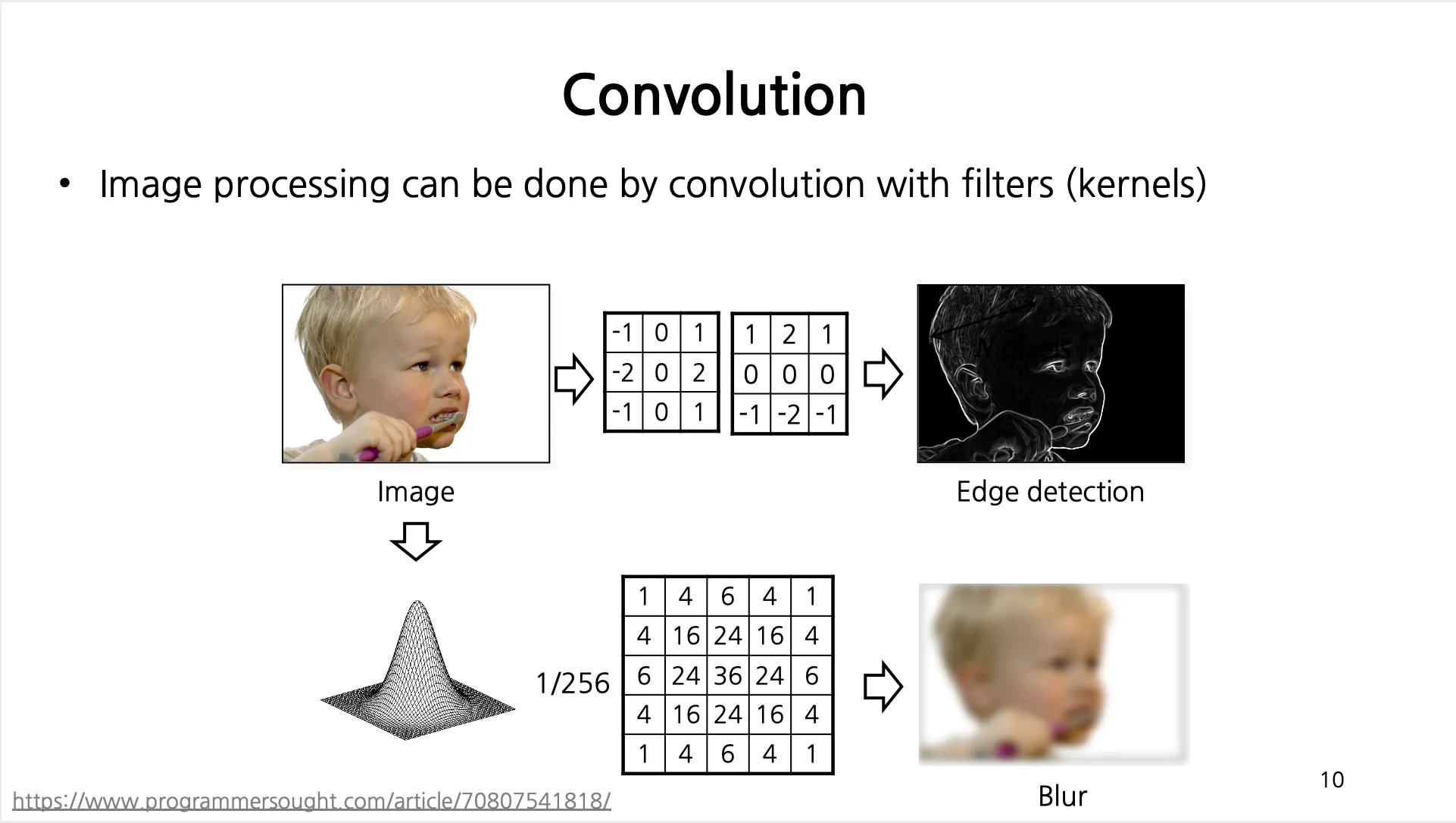
기본적으로 Filters (Kernerls) 와 Convolution 으로 수행됨. Filters 는 Image Processing 의 기본적인 도구이며 Digital Image 에 적용되어 Image 의 특성을 변환하거나 중요한 값들을 추출해낼 수 있음.
•
Convolution Operation 은 유지한 채 Filters 를 변경하면, 완전히 다른 Image Processing 을 구현할 수 있음.
◦
Edge Detection 은 특정 픽셀 좌/우 나 상/하 로 큰 픽셀의 변화가 있는 것을 확인하기 위해서 좌/우 나 상/하 로 크기가 동일하지만 부호가 다른 Filter 를 주어 변화 정도를 파악
◦
Blur 은 특정 픽셀 주변의 픽셀 정보들도 포함하여 weighted sum 을 하여 전체적으로 이미지를 뭉개는 효과를 얻어냄

Convolution

•
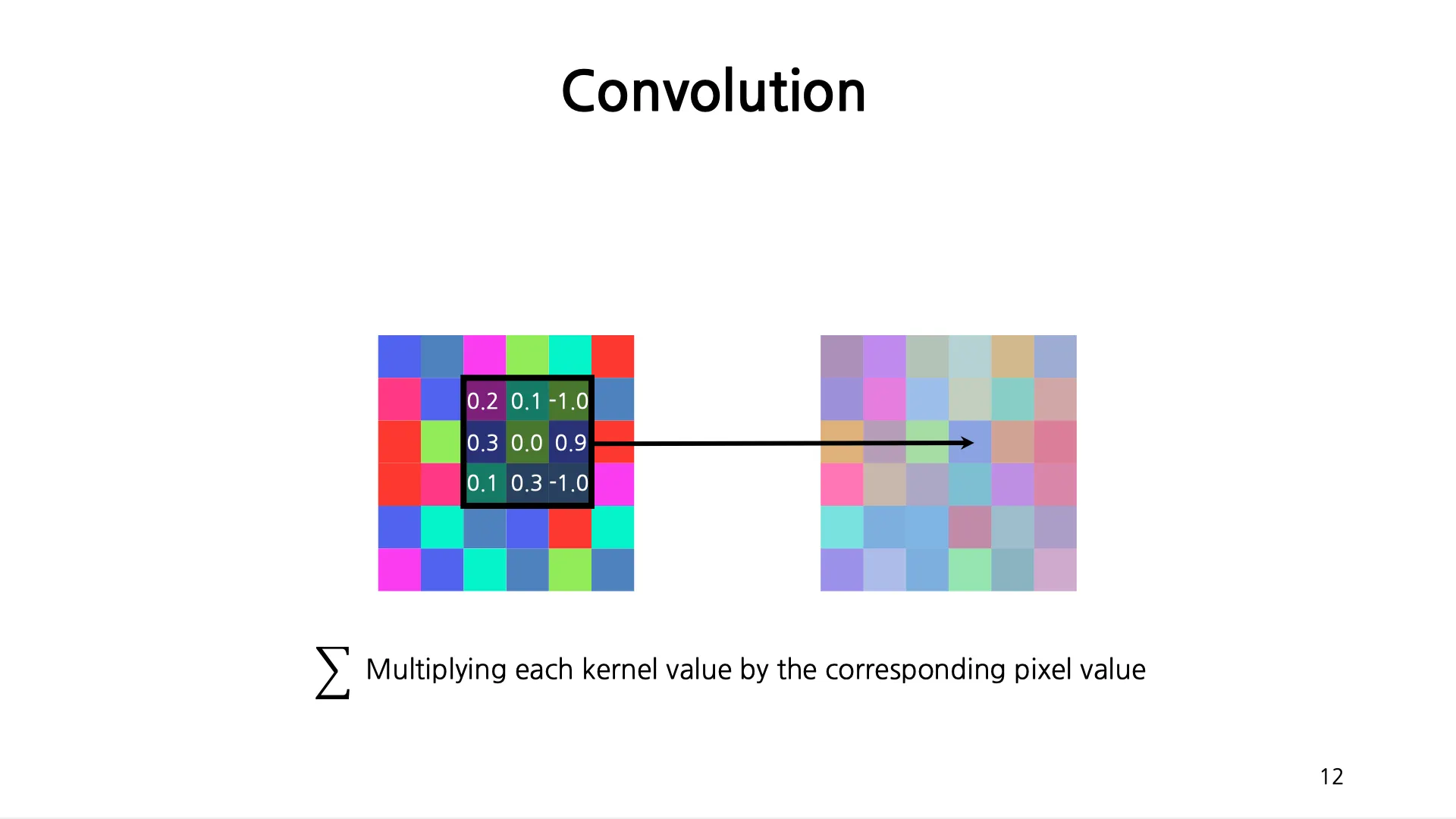
Filter 를 계산하고자 하는 픽셀의 중앙에 두고, Filter 의 값과 기존 이미지간의 픽셀 값을 pixel-wise multiplication 을 진행하여 새로운 픽셀 값을 얻어냄.
•
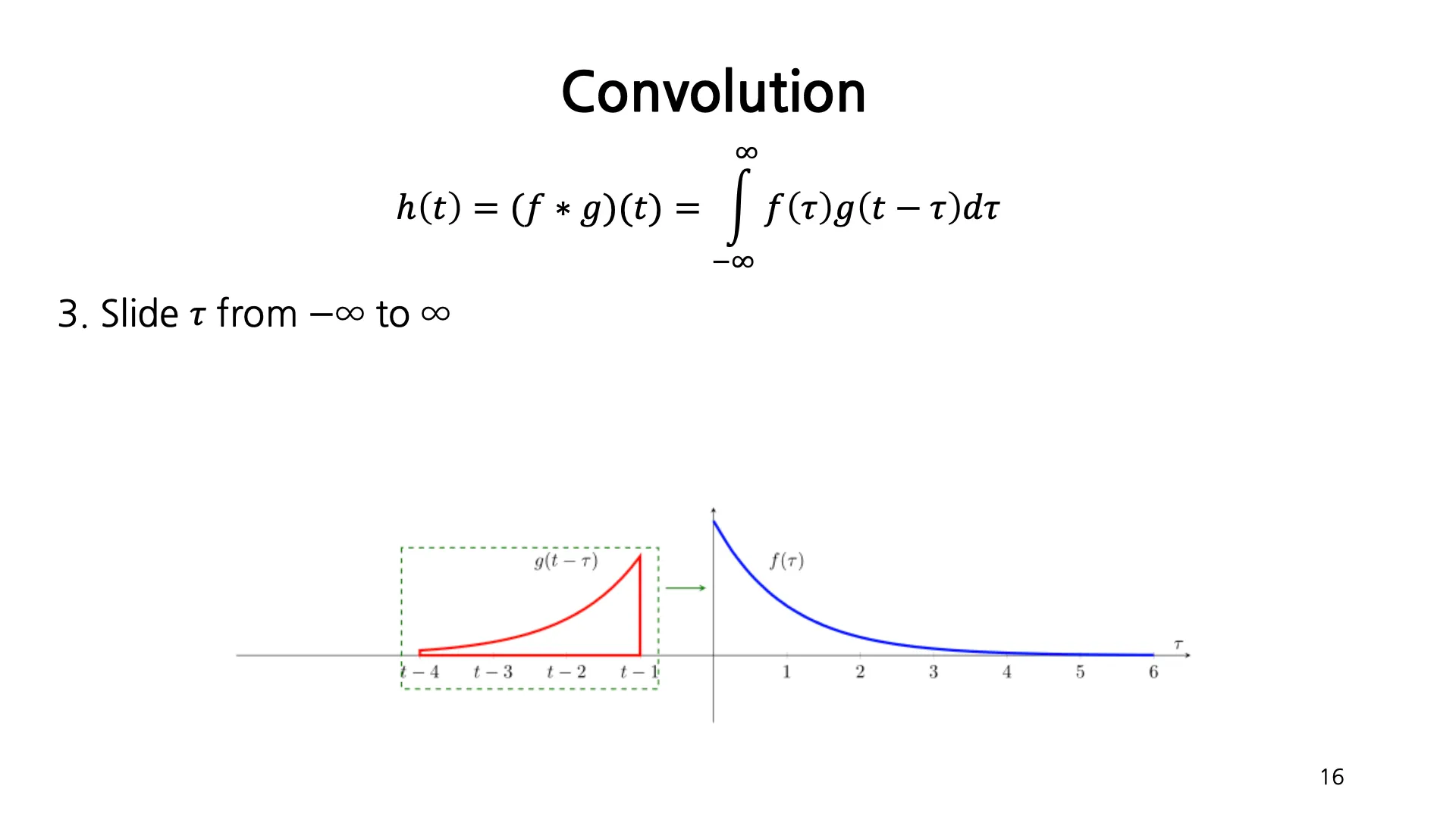
일반적인 Convolution 의 계산은 두 function ff 와 gg 에 대해서 둘 중 하나의 함수를 reverse, shift 하여 서로를 multiply 하고 sum 하는 과정임.
h(t)=(f∗g)(t)=∫−∞∞f(τ)g(t−τ)dτ=∫−∞∞f(t−τ)g(τ)dτ\begin{align*} h(t) = (f*g)(t) = \int_{-\infty}^{\infty}f(\tau)g(t-\tau)d\tau \\ = \int_{-\infty}^{\infty}f(t-\tau)g(\tau)d\tau \end{align*}
•
τ\tau 에 대한 두 함수 ff, gg 를 그린 후 둘 중 하나를 reverse 하고 shift 한 뒤 tt 가 변함에 따라 두 함수 중 하나를 이동시켜가면서 매 순간마다 두 함수의 각 값을 곱한 최종 함수의 밑넓이가 결과적으로 해당 tt 에 대한 convolution hh 값이 됨. tt 를 이동시킴으로써 연속적인 hh 값들을 모두 얻어낼 수 있음.
•
Properties of Convolution
◦
Commutative
a∗b=b∗aa*b=b*a
◦
Associative
(a∗b)∗c=a∗(b∗c)(a*b)*c = a*(b*c)
◦
Cascade Sysetm
(f∗h1)∗h2=gf∗(h1∗h2)=gf∗(h2∗h1)=g(f*h_1)*h_2=g \\ f*(h_1*h_2)=g \\ f*(h_2*h_1)=g
◦
Linear Shift Invariant
▪
Linearity
f1∗h=g1f2∗h=g2Then, (αf1+βf2)∗h=αg1+βg2f_1*h =g_1\\ f_2*h = g_2\\ \mathrm{Then},\ (\alpha f_1 + \beta f_2)*h = \alpha g_1 + \beta g_2
▪
Shift Invariance
f∗h=gThen, f(x−a)∗h=g(x−a)f * h = g \\ \rm{Then},\ f(x-a) * h =g(x-a)
◦
Identity
▪
어떤 hh 가 주어졌을 때, f∗h=ff * h = f 가 될 것인가? → Dirac Delta Function!
▪
t=0t=0 일 때 Dirac Delta Function 과의 Convolution
f∗δ=∫−∞∞f(τ)δ(t−τ)dτ=∫−∞∞f(τ)δ(−τ)dτ=∫−∞∞f(τ)δ(τ)dτ=∫−∞∞f(0)δ(τ)dτ=f(0)∫−∞∞δ(τ)dτ=f(0)f * \delta = \int_{-\infty}^{\infty}f(\tau)\delta(t-\tau)d\tau=\int_{-\infty}^{\infty}f(\tau)\delta(-\tau)d\tau=\int_{-\infty}^{\infty}f(\tau)\delta(\tau)d\tau=\int_{-\infty}^{\infty}f(0)\delta(\tau)d\tau=f(0)\int_{-\infty}^{\infty}\delta(\tau)d\tau=f(0)
▪
t=Tt=T 일 때의 Dirac Delta Function 과의 Convolution
h(T)=f(T), by Shift Invarianceh(T) = f(T),\ \rm{by\ Shift\ Invariance}

Convolution in Discrete and Finite Image

•
기존 Convolution 은 연속적, 무한까지 값을 가질 수 있었지만 이미지의 픽셀은 이산적이고 유한함.
•
Integral 은 Summation 으로 바뀌고 범위가 제한됨.
•
Filter 를 좌/우 로 한 번 뒤집고, 상/하 로 한 번 뒤집어야 하지만 pixel-wise multiplication 을 수행하여 최종적인 값을 얻어냄. (아래는 M×NM\times N 크기의 filter)
g(i,j)=∑m=1M∑n=1Nh(m,n)f(i−m,j−n)g(i,j) = \sum_{m=1}^M\sum_{n=1}^N h(m,n)f(i-m, j-n)
•
정확한 정의에 의해서는 Filter 를 좌/우 로 한 번 뒤집고, 상/하 로 한 번 뒤집어야 하지만 딥러닝에서는 이러한 과정을 진행하지 않음. 하지만 학습이랑 추론 단에서 모두 하지 않기 떄문에 픽셀 정보해석에는 큰 상관이 없음.
•
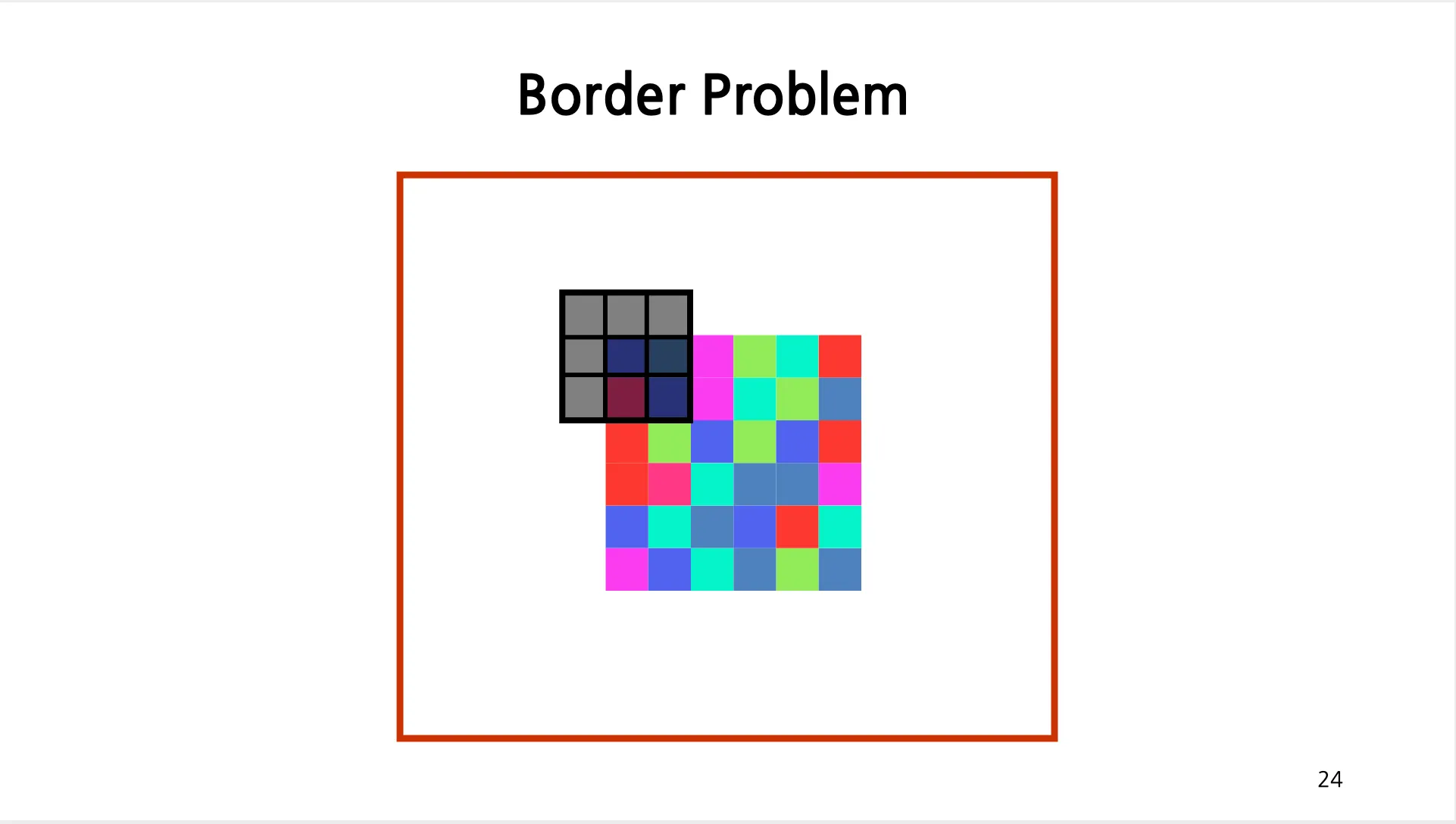
Border Problem
◦
이미지의 경계 부분에서 Filter 를 적용했을 때 경계 밖의 이미지의 픽셀 값이 존재하지 않기 때문에 계산이 불가능한 문제
◦
세 가지 정도의 해결 방법
▪
Ignore - Convolution 이 정의되는 공간의 영역이 줄어들기 때문에 Output Size 가 Input Size 에 비해서 작아지게 됨.
▪
Zero Padding - 0 값으로 이미지의 주변을 padding 하여 계산 가능하도록 변경함. (Standard!)
▪
Reflection Padding - 경계를 중심으로 하여 안쪽의 값을 그대로 reflection 해서 padding 하여 계산 가능하도록 변경함. (잘 쓰이지는 않음)

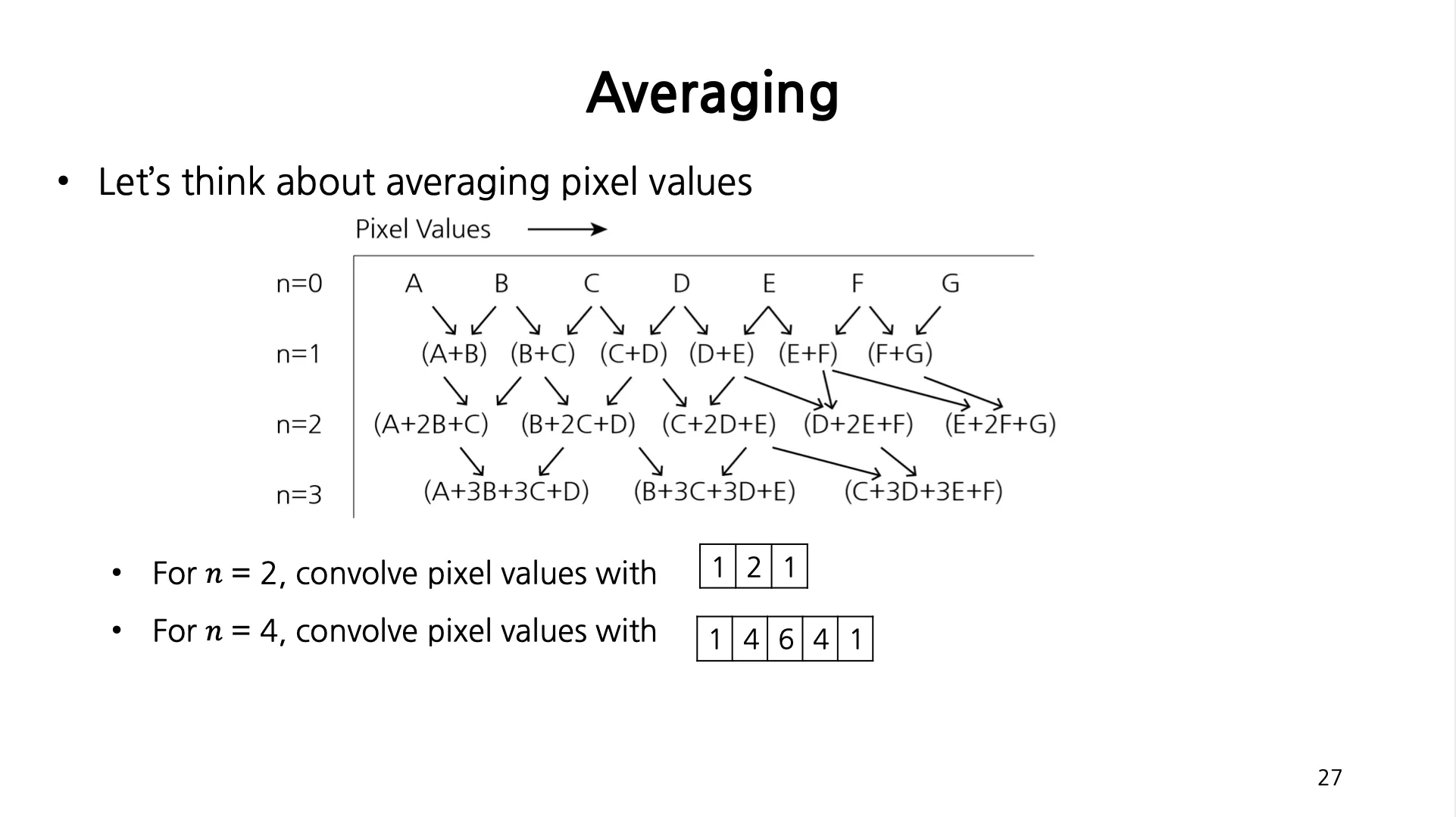
Averaging

•
인접한 픽셀 값을 평균내기 위해서 더한다고 가정해 보았을 때 다음과 같이 [1,2,1][1, 2,1], [1,3,3,1][1,3,3,1], [1,4,6,4,1][1,4,6,4,1] 과 Convolution 한 결과로 볼 수 있음.
•
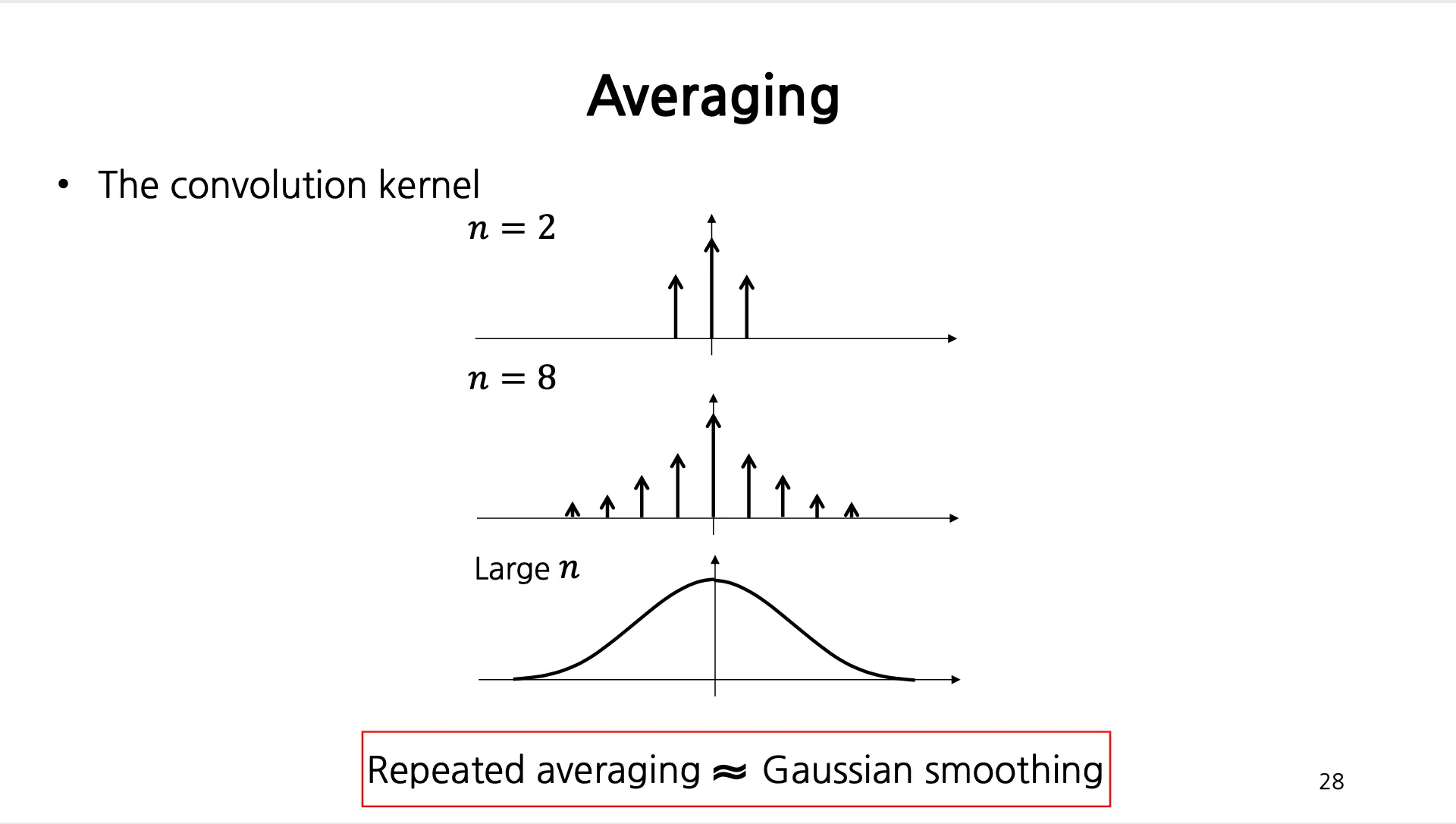
위의 Filter 가 일반적으로 Gaussian Distribution 을 따른다는 것이 밝혀짐. (Gaussian Kernel)
•
Gaussian Kernel
h(i,j)=12πσ2exp⁡(−i2+j22σ2)g(i,j)=12πσ2∑m=1∑n=1exp⁡(−m2+n22σ2)f(i−m,j−m)h(i,j)=\frac{1}{2\pi\sigma^2}\exp(-\frac{i^2+j^2}{2\sigma^2})\\ g(i,j)=\frac{1}{2\pi\sigma^2}\sum_{m=1}\sum_{n=1}\exp(-\frac{m^2+n^2}{2\sigma^2})f(i-m,j-m)
◦
σ\sigma 가 클수록 넓적한 형태가 되고 Filter 의 Size 가 큰 것이 일반적이지만, 잘라서 사용이 가능함.
◦
O(mnpq)O(mnpq) 의 시간 복잡도를 가지기 때문에 필요 이상의 Filter 를 사용하는 것은 좋지 못함. m,nm, n: Image 의 크기, p,qp,q : kernel 의 크기
◦
2D Gaussian 은 1D Gaussian 2개로 나누어서 적용한 것과 완벽히 동일한 연산이기 때문에 (Seperable) 현실에서는 1D Gaussian 2개를 O(n2)O(n^2) 를 O(2n)O(2n) 으로 변경할 수 있기 때문에 효율적임.
g(i,j)=12πσ2∑m=1∑n=1exp⁡(−m2+n22σ2)f(i−m,j−m)=12πσ2∑m=1exp⁡(−m22σ2)∑n=1exp⁡(−n22σ2)f(i−m,j−m)g(i,j)=\frac{1}{2\pi\sigma^2}\sum_{m=1}\sum_{n=1}\exp(-\frac{m^2+n^2}{2\sigma^2})f(i-m,j-m)\\ = \frac{1}{2\pi\sigma^2}\sum_{m=1} \exp(-\frac{m^2}{2\sigma^2}) \sum_{n=1}\exp(-\frac{n^2}{2\sigma^2})f(i-m,j-m)
•
Gaussian Smoothing 의 예시
•
Mean Filtering VS Gaussian Filtering
◦
Mean Filtering 은 3×33\times 3 kernel 의 경우 동일하게 19\frac{1}{9} 의 값을 가진 kernel 을 사용하는 것임.
◦
Mean Filtering 은 Horizontal, Vertical 라인이 보이는 것과 같은 artifact 들을 발생시키는 반면 Gaussian Filtering 은 조금 더 부드러운 결과를 얻을 수 있음.
•
Blur Illusion
•
Median Filter
◦
기존의 Smooting 과정들은 edge 의 구분을 모호하게 만들거나 outlier 에 취약한 경향성을 보여줌.
◦
Median Filter 는 자신의 위치 픽셀을 제외한 N2−1N^2-1 주변 픽셀의 중앙값을 선택하는 방법으로 기존 Smoothing 의 단점을 어느정도 극복할 수 있음.
◦
하지만, Non-linear 한 operation 이기 때문에 convolution 으로 구현할 수 없음.
◦
Salt and Perpper Noise 에서 잘 동작하는 Median Smoothing 과 Gaussian Noise 에서 잘 동작하는 Gaussian Smoothing 의 예시

Cross-Correlation

•
Template Matching 에서 주로 사용되는 방법으로, 두 Image 가 존재할 때 하나의 Image 를 다른 Image 위를 convolution 하면서 각 영역에서의 유사도를 측정하는 방법.
•
수학적으로는 Convolution 은 kernel 의 flipping 이 추가되었을 뿐 Cross-Correlation 과 동일함.
•
Cross-Correlation 의 목적은 다음을 최소화하는 것임.
E(i,j)=∑m=i+1m=i+M∑n=j+1n=j+N[f(m,n)−t(m−i,n−j)]2=∑m=i+1m=i+M∑n=j+1n=j+N=f(m,n)2+t(m−i,n−j)2−2f(m,n)t(m−i,n−j)\begin{align*} E(i,j)&=\sum_{m=i+1}^{m=i+M}\sum_{n=j+1}^{n=j+N}[f(m,n)-t(m-i,n-j)]^2 \\ &= \sum_{m=i+1}^{m=i+M}\sum_{n=j+1}^{n=j+N}=f(m,n)^2 +t(m-i,n-j)^2-2f(m,n)t(m-i,n-j) \end{align*}
Rtf(i,j)=∑m∑nf(m,n)t(m−i,n−j)R_{\rm{tf}}(i,j)=\sum_m\sum_n f(m,n)t(m-i,n-j)
•
위 식에서 고정된 항목을 제외하면 다음과 같은 식을 최대화하는 것과 동일함.
•
하지만, 위 식만을 활용하면 값이 비슷한 영역이 아니라 단순히 곱이 높은 영역이 선택되는 edge case 들이 발생하기 때문에 이를 normalize 하는 시도를 할 수 있음.
Ntf(i,j)=∑m∑nf(m,n)t(m−i,n−j)[∑m∑nf(m,n)2]1/2[∑m∑nt(m−i,n−j)2]1/2N_{\rm{tf}}(i,j)=\frac{\sum_m\sum_n f(m,n)t(m-i,n-j)}{[\sum_m\sum_n f(m,n)^2]^{1/2}[\sum_m\sum_n t(m-i,n-j)^2]^{1/2}}
•
t=ft =f 인 경우를 Auto-Correlation 이라고 함.
•
첨언) Cross-Correlation 의 첫 식에서 f(m,n)2f(m,n)^2 이 영역의 변경에 따라 일정하지 않아서 고정되었다고 볼 수 없지만, 고정을 가정하고 normalize 를 하는 쪽이 연산이 더 간단해서 위와 같이 진행한 것 같음.