Duplicate

Lecture 11 | Homography and Camera Model

형태
Computer Vision
수강 일자
2022/10/10

A Hierararchy of Transformations

•
Translation
◦
Inhomogeneous
x′=x+t\rm x' = x + t
◦
Homogeneous
x′=[I2×2t01×21]x=[I2×2t01×21][x1x21]=[x1+t1x2+t21]\rm x' = \begin{bmatrix} I_{2\times2} & t \\ 0_{1\times 2} & 1 \end{bmatrix}x = \begin{bmatrix} I_{2\times2} & t \\ 0_{1\times 2} & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ 1 \end{bmatrix} = \begin{bmatrix} x_1 + t_1 \\ x_2 + t_2 \\ 1 \end{bmatrix}
▪
2 DoF for translation
▪
Chain 과 inversion 을 적용하기 편리함
•
Euclidean (Rigid) Transform
◦
Inhomogeneous
x′=Rx+t\rm x' = Rx +t
◦
Homogenous
x′=[Rt01×21]x=[Rt01×21][x1x21]=[R[x1x2]+[t1t2]1]\rm x' = \begin{bmatrix} R & t \\ 0_{1\times 2} & 1 \end{bmatrix}x = \begin{bmatrix} R & t \\ 0_{1\times 2} & 1 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \\ 1 \end{bmatrix} = \begin{bmatrix} R\begin{bmatrix}x_1 \\ x_2 \end{bmatrix} + \begin{bmatrix}t_1 \\ t_2 \end{bmatrix} \\ 1 \end{bmatrix}
▪
1 DoF for rotation + 2 DoF for translation → 3 DoF
▪
Disatnce, angle, area, orientation (flipping 이 없다는 뜻임) 을 유지함
▪
Chain of two Euclidean Transforms 은 또다른 Euclidean Transform 임
▪
Rotation 은 원점을 기준으로 일어나기 때문에, 중심의 위치가 중요하고 때문에 rotation 과 translation 의 순서에 따라서 결과도 다름!
→ 보통 컴퓨터비전에서는 rotation 을 먼저, translation 을 다음에 적용함
•
Similarity Transformation
x′=[scos⁡θ−ssin⁡θtxssin⁡θscos⁡θty001]x=[sRt01×21]x\rm x' = \begin{bmatrix} s\cos\theta & -s\sin\theta & t_x \\ s\sin\theta & s\cos\theta & t_y \\ 0 & 0 & 1 \end{bmatrix}x = \begin{bmatrix} sR & t \\ 0_{1\times 2} & 1 \end{bmatrix}x
◦
1 DoF for rotation + 1 DoF for scale + 2 DoF for translation → 4 DoF
◦
Angle 을 유지함
•
Affine Transformation
x′=[a11a12txa21a22ty001]x=[A2×2t01×21]x\rm x' = \begin{bmatrix} a_{11} & a_{12} & t_x\\ a_{21} & a_{22} & t_y \\ 0 & 0 & 1 \end{bmatrix}x = \begin{bmatrix} A_{2\times2} & t \\ 0_{1\times 2} & 1 \end{bmatrix}x
◦
AA 는 non-singular matrix (invertible)
◦
4 DoF for AA + 2 DoF for translation → 6 DoF
◦
Parallelism 은 보존됨
▪
교점이 infinity (ideal points) 인 두 직선을 고려했을 떄, 해당 교점이 tranform 이후에 어떻게 변하는가 → ideal points 로 유지됨 (변환 후에도 평행이라는 뜻!)
▪
Line at infinity 가 line at infinity 로 그대로 대응되는 것도 평행이 그대로 유지된다는 것을 의미함 (Line 의 transform 은 H−TH^{-T})
l∞′=HA−Tl∞=[A−T0−tTA−T1][001]=[001]=l∞l'_{\infty}=H_A^{-T}l_{\infty} =\begin{bmatrix} A^{-T} & 0 \\ -t^TA^{-T} & 1 \end{bmatrix} \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} = l_{\infty}
•
Projective Transformation
x′=[Atv2×1v]x\rm x' = \begin{bmatrix} A & t \\ \rm v_{2\times 1} & v \end{bmatrix}x
◦
Ideal points 가 ideal points 로 매핑되지 않을 수 있기 때문에 parallelism 이 깨짐
◦
4 DoF for AA + 2 DoF for translation + 2 DoF for v\rm v → 8 DoF
◦
v=0v =0 이 가능함!!!
◦
Conlinearity, cross-ratio (ratio of ratio of length) 가 보존됨

Overview: Camera Projections

•
Camera Model 은 Object, Camer, Image Center 로 구성된 체계
•
가장 기본적인 Camera Model 은 Pinhole Camera Model

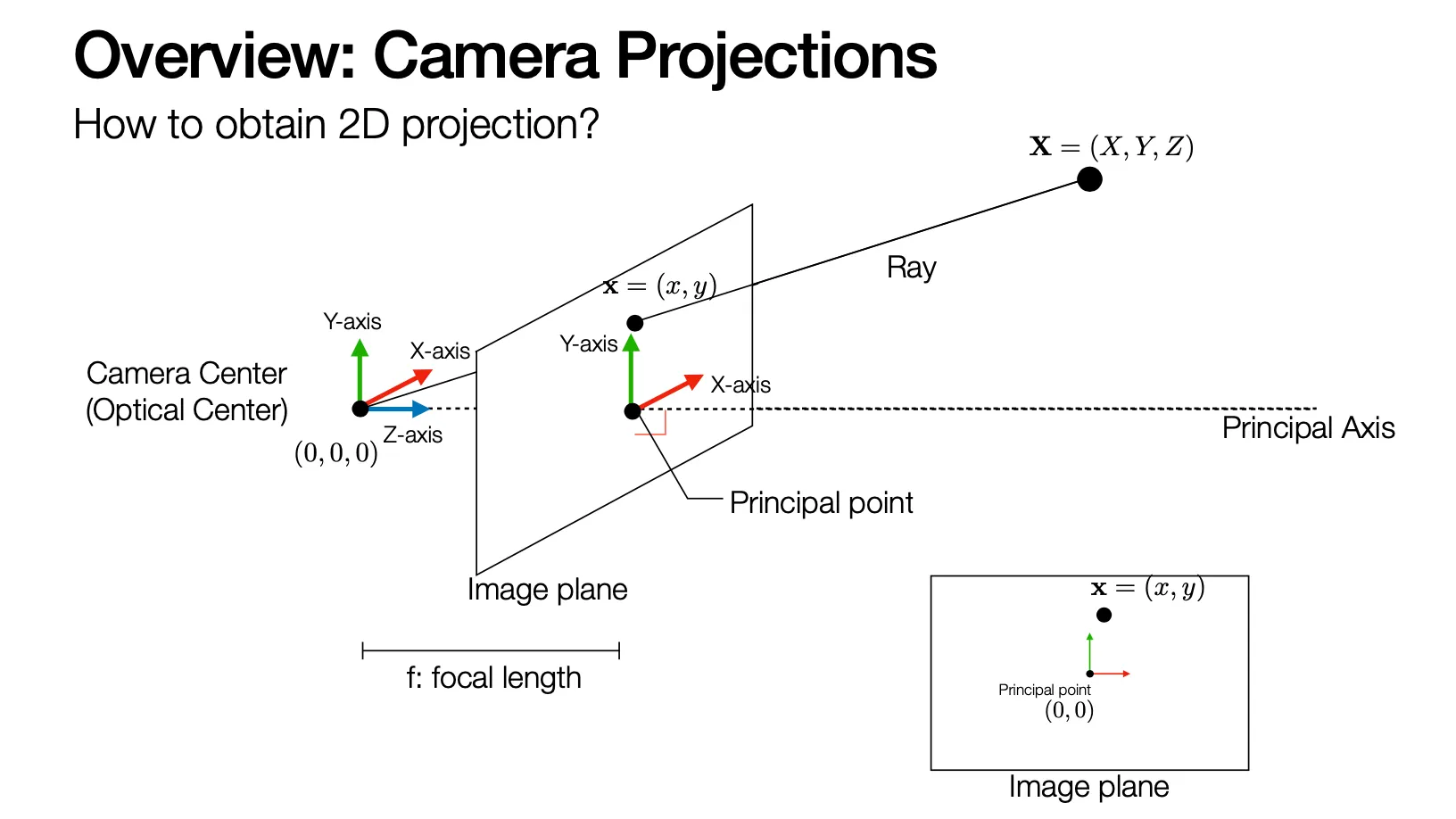
Camera Projections

•
ff (focal length): camera center 부터 image plane 까지의 거리
•
Principal Axis: image plane 과 수직이고 camera center 를 지나는 축
•
Principal Point: principal axis 가 image plane 를 지나는 점
•
Ray: object 로부터 camera center 와 이어지는 선
•
Projection: object 의 각 점을 camera center 와 연결한 ray 와 image plane 이 만나는 점들로 구성된 상
•
상은 실제로 pinhole 뒤쪽에 upside-down 으로 맺히지만 그림의 편의상 pinhole 앞쪽에 image plane 을 그림

Camera Intrinsic Parameters

•
상의 크기는 어떻게 될 것인가?
◦
닭음과 그 비율을 이용해 계산할 수 있음!
(X,Y,Z)T→(fXZ,fYZ)(kX,kY,kZ)T→(fXZ,fYZ)(X,Y,Z)^T \rarr (f\frac{X}{Z}, f\frac{Y}{Z}) \\ (kX,kY,kZ)^T \rarr (f\frac{X}{Z}, f\frac{Y}{Z})
◦
같은 ray 위에 있는 점들은 같은 점으로 projection 되기 때문에 kk 에 관계없이 projection 은 같음!
•
Camera Projection 을 matrix 로 표현?
[f0000f000010](XYZ1)=(fXfYZ)\begin{bmatrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0\\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{pmatrix} X \\ Y\\ Z\\ 1 \end{pmatrix} = \begin{pmatrix} fX \\ fY\\ Z \end{pmatrix}
◦
입력은 3D3D homogenous, 출력은 2D2D homogeneous
◦
3×43\times4 matrix 를 camera matrix 라고 부름
◦
camera matrix 는 실제로 intrinsic matrix 와 extrinsic matrix 로 나누어짐
[f000f0001][100001000010]\begin{bmatrix} f & 0 & 0 \\ 0 & f & 0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0 \end{bmatrix}
▪
앞이 intrinsic (focal length 와 관련), 뒤가 extrinsic (부가적인 transformation)
▪
1 DoF
•
Offset Adding: 이미지 픽셀 coordinate 에서는 보통 origin 을 corner 에 두기 마련이므로, origin 을 옮겨주기 위한 offset adding 과정이 필요할 수 있음
[f0px0fpy001][100001000010](XYZ1)\begin{bmatrix} f & 0 & p_x \\ 0 & f & p_y\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{pmatrix} X \\ Y\\ Z\\ 1 \end{pmatrix}
◦
3 DoF
•
Unit Change: 3D coordinate 의 physical unit 을 2D pixel coordinate 의 pixel unit 으로 변경해주기 위한 scalar factor 를 도입하는 과정이 필요할 수 있음
[mxf(∼αx)0px0myf(∼αy)py001][100001000010](XYZ1)\begin{bmatrix} m_xf(\sim\alpha_x) & 0 & p_x \\ 0 & m_yf(\sim\alpha_y) & p_y\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{pmatrix} X \\ Y\\ Z\\ 1 \end{pmatrix}
◦
위는 4 DoF
◦
Pixel 이 square 이 아니라 tilted (sheared) 된 경우 추가적인 skew parameter ss 를 도입할 수 있음
[mxf(∼αx)spx0myf(∼αy)py001][100001000010](XYZ1)\begin{bmatrix} m_xf(\sim\alpha_x) & s & p_x \\ 0 & m_yf(\sim\alpha_y) & p_y\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{pmatrix} X \\ Y\\ Z\\ 1 \end{pmatrix}
◦
위는 5 DoF
•
최종적인 Intrinsic Parameter matrix 는 다음과 같음
K=[αxsx00αyy0001]K = \begin{bmatrix} \alpha_x & s & x_0 \\ 0 & \alpha_y & y_0\\ 0 & 0 & 1 \end{bmatrix}

Focal Length

•
Focal length 가 크면 장면이 커짐 (zoom-in) → fz\frac{f}{z} 가 크기 때문에 상이 커지는 것임
•
Focal length 가 작으면 큰 object, view 를 볼 수 있음 (Field of View 가 커짐)
•
Zoom 을 하기 위해서는 큰 focal length 를, 큰 object 를 보기 위해서는 작은 focal length 를 사용하면 됨