VGGNet

분야

Network Architecture

리뷰 날짜

2021/05/30

본 포스트에서는 image recognition task 로 유명한 CNN 을 depth 에 대해서 분석한 논문에 대해서 살펴보려고 합니다. 리뷰하려는 논문의 제목은 다음과 같습니다.

“Very Deep Convolutional Networks for Large-Scale Image Recognition”

논문에 대한 내용을 직접 보시고 싶으신 분은 이곳을 참고하시면 좋습니다.

Objective

논문의 배경은 공공 거대 이미지 저장소인 ImageNet 과 고성능 연산기의 발전에 힘입어 Convolutional Network 가 computer vision 의 영역에서 좋은 성능을 보이는 것으로 일반화가 되자, 이것의 시초라고 할 수 있는 Krizhevsky et al. 을 성능적으로 개선하려는 많은 연구가 시도되던 것으로부터 시작합니다.

일례로, Zeiler & Furgus 가 작성한 "Visualizing and understanding convolutional networks" 에서는 첫 번째로 등장하는 convolution layer 의 window size 와 stride 를 작게 설계하는 것이 성능적으로 유의미하다는 것을 알려주었고, Sermanet et al. 에서는 이미지에 multi-scale 을 적용해 train, test 하는 것이 성능을 높일 수 있다는 것을 알려주었습니다.

논문에서는 마찬가지로 Convolutional Network 의 성능 개선에 대한 시도로, 구조가 가질 수 있는 다른 중요한 aspect 인 깊이(depth)에 대해서 중점적으로 분석하는 시도를 합니다. 자세히는, Convolutional Network 의 깊이와 관련 있는 요소가 성능에 미치는 관계에 대해서 알아보는 것을 목적으로 했습니다.

Convolutional Network Configuration

같은 상황에서 구조의 깊이에 따른 공정한 성능 비교를 하기 위해서 논문에서는 Ciresan et al., Krizhevsky et al. 에서 가져온 architecture 구조로 모델의 뼈대를 만듭니다.

Architecture

논문에서 사용한 Convolutional Network 의 기본 세팅에 대한 내용을 전달합니다. 단순한 정보전달이기 때문에 나열식으로 정리해드리려고 합니다. 이 부분은 한 번 훑어만 보셔도 좋을 것 같습니다.

•

224×\times×224 size 의 input image 를 사용했습니다.

•

Input image 의 전처리로 RGB 값의 평균을 각각의 pixel 에서 뺄셈했습니다.

•

Convolution Layer 의 filter 로 3×\times×3 receptive field 를 사용했습니다. 이 때, output vector 의 spatial dimension 을 유지하기 위해 stride 와 padding 모두 1을 사용했습니다. 

•

1×\times×1 filter 를 사용하는 Convolutional Layer 를 구조 일부에 사용했습니다.

•

Spatial Pooling 을 위해서 5 개의 Max-Pooling Layer 를 사용했습니다. 이는 2×\times×2 pixel window 와 stride 2 를 가져 dimension 을 가로, 세로로 1/2 로 줄입니다.

•

구조의 마지막 부분에 3 개의 Fully-Connected Layer 를 사용했고 각각 앞에서부터 4096 channel, 4096 channel, 1000 channel 을 가집니다. 마지막 1000 channel 은 ILSVRC dataset 의 1000 개 class 에 기인한 값입니다.

•

모든 Hidden Layer 는 ReLU 를 사용해 non-linearity 를 부여했습니다.

•

한 가지 구조만 빼고 전부 LRN 을 사용하지 않았습니다.

Configurations

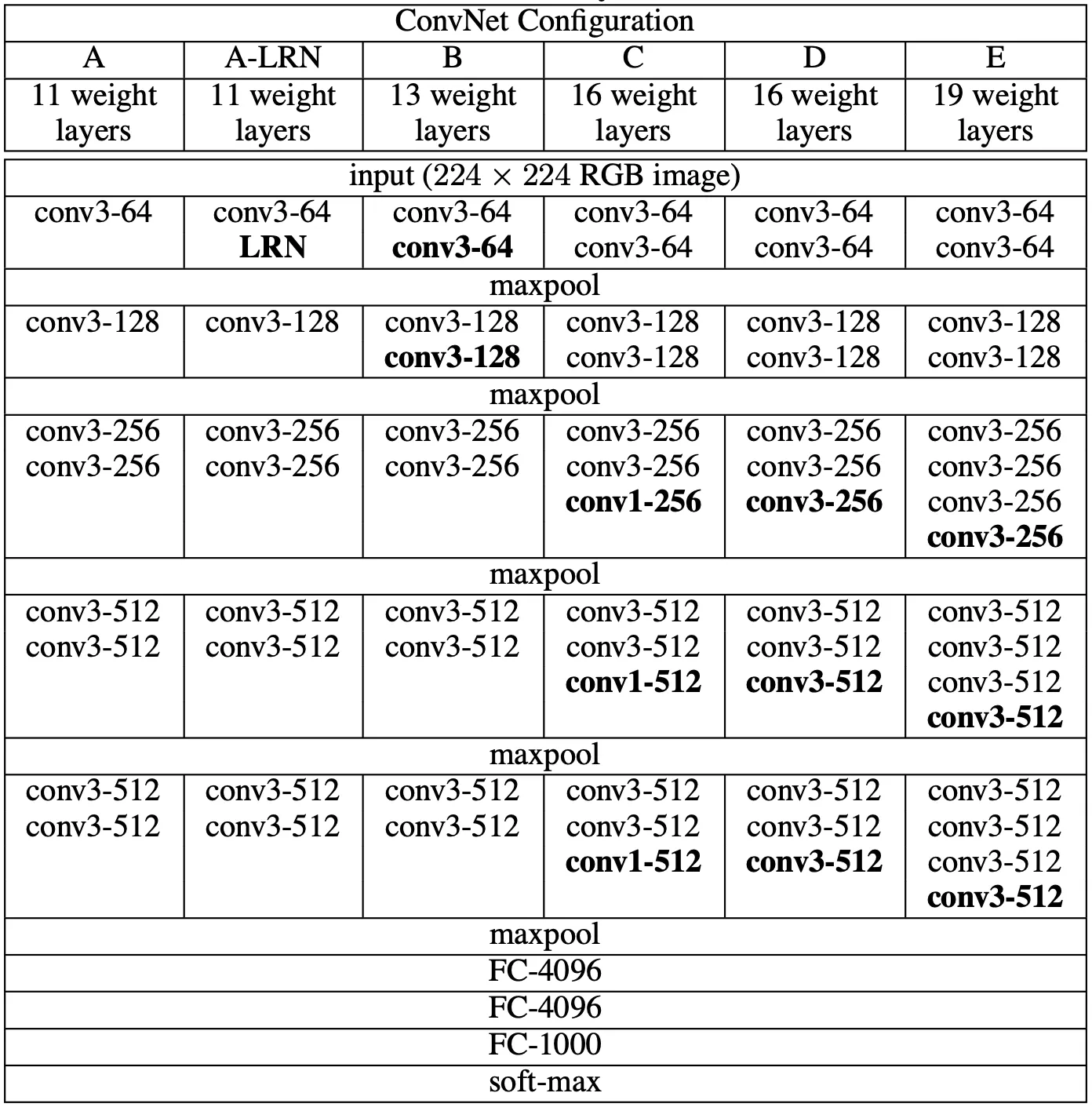
논문에서 사용한 Convolutional Network 의 종류들을 세부적으로 전달합니다. 전체적으로는 위의 Architecture 에 언급한 사항을 따르지만, 세부적으로는 각기 다른 6 개의 Convolution Network 를 사용했습니다. 아래는 그 세부적인 구조를 나타낸 도식표입니다. 각 열이 하나의 Convolution Network 를 의미합니다.

논문에서 사용한 Convolutional Network 의 구조들

위의 도식표를 보시면 아시겠지만, 각각의 A~E 까지의 Convolution Network 의 depth 가 각기 다릅니다. 자세히 들여다 보시면, Convolution Layer 의 channel 수가 64 부터 시작하여 512 가 될 때까지 2배씩 증가하는 것을 보실 수 있습니다. 더욱이, 각각의 Convolutional Network 가 가진 학습 parameter 의 수 또한 상이합니다.

각 Convolution Network 별 parameter 수 (단위: 백만)

위 표에서 보이는 parameter 개수들은 논문에서 제시한 구조보다 깊이가 더 얕은 Sermanet et al. 보다 오히려 적다고 합니다.

Discussion

논문에서 사용한 Convolutional Network 의 Architecture 와 Configuration 은 ILSVRC 2012, 2013 에서 높은 성능을 보였던 network 과는 많이 달랐습니다.

먼저, 상대적으로 큰 receptive field filter 를 사용한 Zeiler & Furgus 의 논문이나 Krizhevsky et al. 등에 비해서 상대적으로 매우 적은 3

\times

3 recpetive field filter 를 사용했습니다. 특히, 7

\times

7 recpetive field filter 를 사용하는 것과 같은 output vector dimension 을 내는 3

\times

3 recpetive field filter 를 3 개 연달아 사용한 구조를 사용했습니다. 논문에서는 이렇게 작은 receptive field filter 를 사용해서 다음과 같은 것들을 얻고자 했습니다.

큰 recpetive field filter 를 적게 사용하는 것보다 작은 receptive field filter 를 많이 사용하는 것이 non-linear rectification layer 를 더 많이 사용하여 activation function 을 상대적으로 많이 적용하게 되고 decision function 을 discriminative 하게 만들 수 있습니다. 

학습에 필요한 parameter 의 수를 줄였습니다. Input, output vector 의 channel 수를 CCC 라고 하면, 7×\times×7 recpetive field filter 1 개는 49C249C^249C2 개의 parameter 를 가지는 반면에  3×\times×3 recpetive field filter 3 개는 3×9C2=27C23\times9C^2=27C^23×9C2=27C2 개의 parameter 를 가집니다.

다음으로, Lin et al. 에서 보인 것과 같이 1

\times

1 recpetive field filter 를 곳곳에 사용했습니다. 논문에서 사용한 1

\times

1 recpetive field filter 는 input 과 output vector 의 channel 수가 같기 때문에 linear projection 이지만, 이 layer 의 추가로 인해 receptive field 의 변화 없이(이 layer 의 존재유무와 관계 없이 뒤에 이어지는 Convolution Layer 의 receptive field 가 동일하다는 뜻입니다) non-linear rectification layer 가 추가되는 효과가 있습니다.

Classification Framework

논문의 Classification Framework 세션에서는 Training, Evaluation 에 대한 디테일을 소개합니다.

Training

논문에서 사용한 Training 의 configuration 에 대한 내용을 전달합니다. 단순한 정보전달이기 때문에 나열식으로 정리해드리려고 합니다. 추가적인 내용은 나열 밑에 디테일하게 설명드리려고 합니다.

•

일반적인 Training configuration 은 Krizhevsky et al. 의 것을 따릅니다.

◦

단, 뒤에서 후술하겠지만, multi-scale training image sampling 은 논문에서 변형하여 사용합니다.

•

학습의 목적은 multinomial logistic regression 입니다. Multi-class classification 으로 보셔도 무방합니다.

•

Mini-batch gradient descent(batch size 256) 를 사용했고, momentum(0.9) 을 적용했습니다.

•

L2 weight regularization(λ=5×10−4\lambda=5\times10^{-4}λ=5×10−4) 을 적용했습니다.

•

Learning rate 는 초기에 10−210^{-2}10−2 로 시작하여 validation set accuracy 가 개선되지 않을 때마다 110\frac{1}{10}101​ 배를 합니다.

◦

논문의 경우에서는 실제로 learning rate 가 3번 감소했으며 370K iterations, 74 epoch 만에 학습이 종료되었다고 합니다.

◦

Krizhevsky et al. 보다 많은 수의 parameter 를 가지고 있었음에도 수렴에 적은 수의 epoch 이 필요했던 이유로

깊은 깊이와, 작은 receptive field filter 를 사용해서 implicit regularization 이 되었기 때문 (7×\times×7 recpetive field filter 1 개를  3×\times×3 recpetive field filter 3 개로 바꾸어 학습에 필요한 parameter 수가 줄어든 것을 의미합니다)

Convolution Network A 를 학습한 뒤 이 parameter 를 사용해 다른 Convolutional Network 의 학습에 Pre-Initialization 을 했기 때문

으로 보고 있습니다.

•

Pre-Initialization 이 적용되지 않는 weight 들에는 normal distribution N(0,0.01)N(0,0.01)N(0,0.01) 에서 랜덤하게 sampling 한 값으로 initialize 했습니다.

•

224×\times×224 의 고정된 input size 를 가지기 위해서 rescaled training image 에서 랜덤하게 crop 한 image 를 사용했습니다. 이 때, data augmentation 을 위해서 랜덤한 좌우 반전, RGB 색상 shift 등을 사용했습니다.

Training Image Rescaling

논문에서는 training 에 사용할 image 를 앞서 말씀드린 data augmentation 의 관점에서 특별한 방법으로 만들어냅니다. 이를 설명하기 위해서 필요한 변수인

S

가 무엇인지부터 설명드리려고 합니다.

S

는 isotropically-rescaled training image 에서 짧은 변의 픽셀 수 입니다. 여기서 isotropically-rescaled 는 "image 의 가로, 세로 비율을 유지하면서 크기를 조절한다" 는 의미를 가지고 있습니다. 만약 원하는 input image 의 size 가 224

\times

224 인데,

S=224

라면 가장 짧은 변을 기준으로 cropping 을 진행하면 되고,

S\geq224

라면 image 의 일부 부분을 기준으로 cropping 을 진행하게 되는 것입니다.

논문에서는 이러한

S

를 가지고 training image 를 생성하는 두 가지의 접근을 사용합니다.

첫 번째로, 고정된

S

를 사용하는 방법입니다. 이는 앞서 언급했던 Krizhevsky et al. 이나 Zeiler & Furgus 의 논문에서 사용한 방법입니다. 논문에서는

S=256

일 때 먼저 학습을 진행하고,

S=384

일 때 앞서 학습을 진행한 결과로 parameter 를 initialize 하고 initial learning rate 를

10^{-3}

으로 설정했습니다.

두 번째로,

[S_{\min},S_{\max}]

의 닫힌 구간에서

S

를 random sampling 하는 방법입니다. 논문에서는

[256, 512]

의 구간을 사용했습니다. 이 방법은 데이터에서 object scale 의 다양성을 부여한다는 측면에서 장점을 가집니다. (같은 사진이라도 이미지를 키운 후 자르면 scale 이 큰 이미지가 나오는 현상을 말하는 것입니다) 이는 data augmentation 의 관점에서 scale jittering 으로 볼 수 있습니다. 논문에서는 training speed 의 이슈로

S=384

일 때 학습된 parameter 를 initialize 에 사용했다고 합니다.

Testing

논문에서는 test 에 사용할 image 를 train 에서 사용할 image 와는 다르게 다양한 크기의 input 에 대해서 사용하면 어떨까에 대한 새로운 제안을 합니다. 개인적으로, 이 부분이 생소하고 낯설으면서도 신기했습니다. 이를 설명하기 위해서 필요한 변수인

Q

가 무엇인지부터 설명드리려고 합니다.

Q

는 isotropically-rescaled training image 에서 짧은 변의 픽셀 수 입니다. 엥?

S

랑 같은 것 아니냐고 여쭤보실 수 있습니다. 네, 그치만

Q

는

S

와 값이 같을 필요는 없습니다.

논문에서는 이러한

Q

를 가지고 evaluation 을 하는 두 가지의 접근을 사용합니다.

첫 번째로, 고정된 Input Size 를 사용하는 방법입니다. 이 방법을 Multi-Crop Evaluation 이라고 합니다. Test image 를 동일한, 공정된 size 로 여러개를 crop 하여 test image 를 형성하고 evaluation 하는 방법입니다. 논문에서는 하나의

Q

당 50 개의 crops 를 사용해 최종적으로 150 crops 로 evaluation 을 진행했습니다.

두 번째로, 유동적인 Input Size 를 사용하는 방법입니다. 이 방법을 Dense Evaluation 이라고 합니다. 이 경우는

Q

를

S

와는 다르게 자르기 위해서 조절하는 것이 아니라 실제로

Q

를 통해 조절된 image 자체를 사용하기 위한 값으로 보는 것입니다. 다양한 크기의 input 에 대해서 testing 를 하기 위해 논문에서는 다양한

Q

를 사용하여 testing image 를 준비합니다. 하지만, 이렇게 된다면 Fully-Connected Layer 에 들어가기 전에 Flatten 한 이후 생성된 vector 의 dimension 이 input 마다 달라 이후에 dimension mismatch 가 날 것입니다. 이를 핸들링하기 위해서 논문에서는 training 할 때 사용했던 network 의 Fully-Connected Layer 를 대응되는 Convolutional Layer 로 변환하여 Fully Convolutional Network 를 만듭니다.

여기서 대응되는 Convolutional Layer 라 함은 앞선 Layer 의 output 의 channel dimension 을 제외한 shape 을 filter 크기로 가지고, 기존의 Fully-Connected Layer 와 같은 크기의 output channel 을 가지는 Convolutional Layer 입니다. 눈치채신분들도 계시겠지만, Flatten 이후에 행렬곱을 하는 기존의 Fully-Connected Layer 와는 달리 Flatten 을 하지 않고 Inner Product 를 하는 것과 동일합니다.

Test image 를 Fully Convolutional Network 에 통과시키고 나온 output 인 class score map 은 학습 데이터와 같은 사이즈라면

1\times1\times1000

의 형태이겠지만, 그것과 다르다면

N\times M \times1000

의 형태가 될 것입니다. 이들을 모두 Softmax 에 넣을 수 있는 형태로 만들어주기 위해서 Sum-Pooling 을 진행합니다. (

N\times M

의 값을 모두 더해 최종적인 score 를 뽑아내는 것입니다.)

Implementaion Detail

논문에서 구현한 training + testing 에 대한 구현은 C++ Caffe toolbox 에 public 하게 공개되어있다고 합니다. 다만, training + evaluation 을 multiple GPU 로 동시에 진행할 수 있도록, multiple sacle evaluation 을 multiple GPU 로 동시에 진행할 수 있도록 하는 modification 이 코드에 포함되어 있다고 합니다. 실제로 training image batch 를 동시에 돌리기 위해 GPU 를 parallel 하게 배정했고, GPU batch gradient 가 계산되면 full batch 의 gradient 를 구하기 위해 더해진 후 평균을 구한다고 합니다. 이러한 gradient computiation 은 GPU 마다 synchronous 되어 있기 때문에 동시에 진행하는 것이 가능하고, 4 GPU 를 사용했을 때 single CPU 를 사용할 때보다 3.75 배 가량 빠르게 학습되었다고 합니다. NVIDIA Titan Black GPU 를 사용했으며, 그 결과 각 Convolutional Network 마다 2~3 주의 시간이 학습에 소요되었다고 합니다.

Classification Experiments

논문에서는 앞서 말씀드린 구조와 training/testing 디테일들을 바탕으로 classification experiment 를 진행합니다. 먼저, 사용한 dataset 에 대한 내용은 다음과 같습니다.

Dataset

논문이 사용한 데이터셋은 ILSVRC-2012 dataset 입니다. 이는 1000 개의 class 를 가지고 있고 training data 1.3M 개, validation data 50K 개, test data 100K 개를 포함하고 있습니다.

논문에서 사용한 evaluation metric 은 top-1 error 와 top-5 error 입니다. 둘 모두 multi-class classification error 로 top-1 error 의 경우에는 전체 trial 중 잘못 classify 한 것의 비율이며, top-5 error 의 경우에는 전체 trial 중 모델이 산출한 softmax 결과의 최대 5 class 안에 옳은 class 가 존재하지 않은 것의 비율입니다.

다음으로, 논문에서 진행한 각 classification experiments 에 대한 내용은 다음과 같습니다.

Single Scale Evaluation

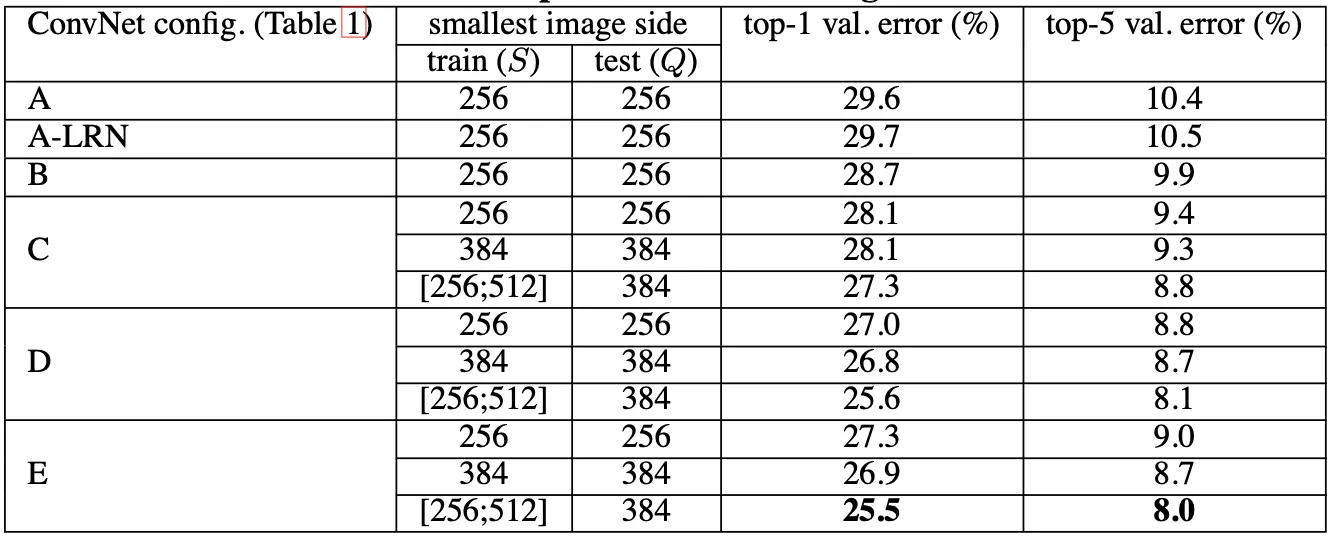
논문에서 가장 먼저 보여주는 것이 고정된

Q

에 대해서 evaluation 한 결과입니다. 고정된

S

를 사용한 경우,

Q=S

로 사용했고, 닫힌 구간의

S

를 사용한 경우

Q=\frac{1}{2}(S_{\min} + S_{\max})

로 사용했습니다. 결과는 아래의 표에 나타난 것과 같습니다.

가장 먼저 보이는 것은 Local Response Network 가 성능을 개선하지 못했다는 점입니다. A 와 A-LRN 의 metric 차이가 거의 없으며, 이 때문에 논문에서는 B~E 에서 LRN Layer 를 넣지 않았다고 합니다.

다음으로 전체적으로 A~E 로 가면서 Convolutional Network 의 depth 가 깊어질 수록 error 가 작아지는 점을 볼 수 있습니다. 여기서 주목할 점은 같은 depth 를 가진 C 와 D 중에는 1

\times

1 recpetive field filter 를 사용한 C 보다 3

\times

3 recpetive field filter 를 사용한 D 가 더 높은 성능을 보였다는 점입니다. 물론 C 가 B 보다 더 높은 성능을 보였다는 점에서 추가적인 non-linearity 의 부여가 높은 성능을 가져다 주었다고 볼 수 있지만, 그것 못지 않게 non-tivial Convolution Layer 를 통한 context capturing 또한 성능에 중요한 역할을 하는 것임을 볼 수 있었습니다.

또한 위 표에는 나와있지 않지만, B 에서 3

\times

3 recpetive field filter 2 개가 연달아 있는 구조를 5

\times

5 recpetive field filter 로 바꾸어 성능을 비교해 보았는데, 바꾼 후에 top-1 error 가 7% 정도 상승했다고 합니다. 이를 통해 깊고 작은 Convolutional Layer 를 쓰는 것이 얕고 큰 Convolutional Layer 를 쓰는 것보다 좋은 성능을 보임을 알 수 있었습니다.

마지막으로 닫힌 구간 내에서의

S

에서 sampling 하여 training 한 방식(scale jittering) 이 성능에 긍정적으로 유의미한 결과를 보여준다는 사실을 알 수 있었습니다. 이는 training set augmentation 이 다양한 scale 의 이미지에 대한 context 를 학습할 수 있었기 때문으로 보고 있습니다.

Multi-Scale Evaluation

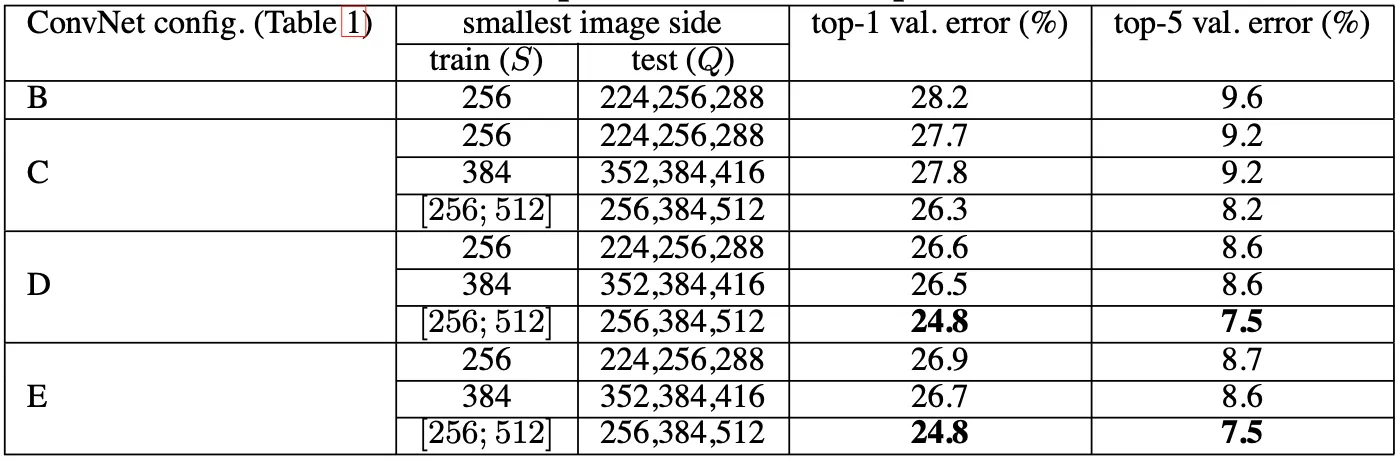
다음으로 보여주는 것이 scale jittering 을 test 에 적용한 결과입니다. 고정된

S

를 사용한 경우

Q=\{S-32, S, S+32\}

의 세 가지 종류를 사용했고, 닫힌 구간의

S

를 사용한 경우

Q=\{S_{\min},\frac{1}{2}(S_{\min}+S_{\max}), S_{\max})\}

의 세 가지 종류를 사용했습니다. 결과는 아래의 표에 나타난 것과 같습니다.

가장 먼저 보이는 것은 scale jittering 을 test 에 적용한 것이 적용하지 않은 것보다 높은 성능을 보여주었다는 점입니다. 이는 위의 Single Scale Evaluation 에서 보여주었던 표와 여기서 제공한 표와의 비교를 통해 알 수 있습니다.

마찬가지로, 깊은 Convolutional Network 였던 D 와 E 에서 가장 낮은 top-1, top-5 error 를 보여주었고, training set 에도 scale jittering 을 사용하는 것이 성능이 좋았다는 것을 다시 한 번 볼 수 있었습니다.

Multi-Crop Evaluation

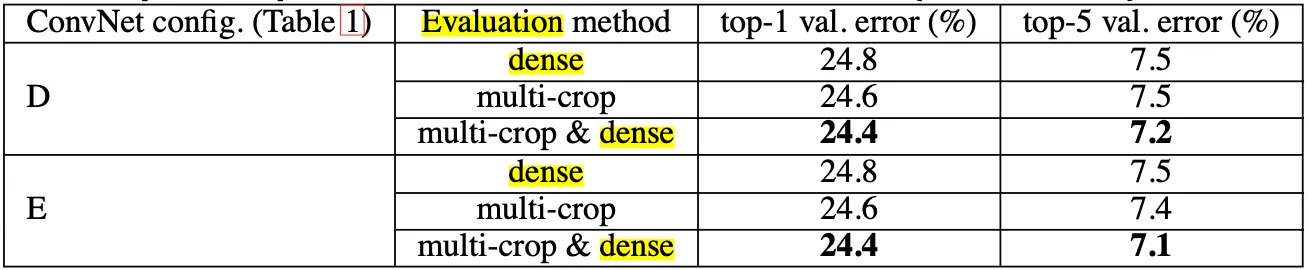
다음으로 보여주는 것이 testing 부분에서 말씀 드렸던 dense evaluation 과 multi-crop evaluation 을 각각 적용해보고 얻은 성능에 대한 내용입니다. 결과는 아래의 표에 나타난 것과 같습니다.

Multi-Crop evaluation 이 약간 더 성능은 좋았지만, sampling 과정이 필요하기 때문에 속도가 느린 단점이 있습니다. 두 방법 모두를 사용해 나온 Softmax output 을 average 하는 방식을 사용한 것이 위 표에 나타난 multi-crop & dense 의 경우이며 이 경우가 가장 성능이 높게 나타났다는 것을 알 수 있습니다.

Convolutional Network Fusion

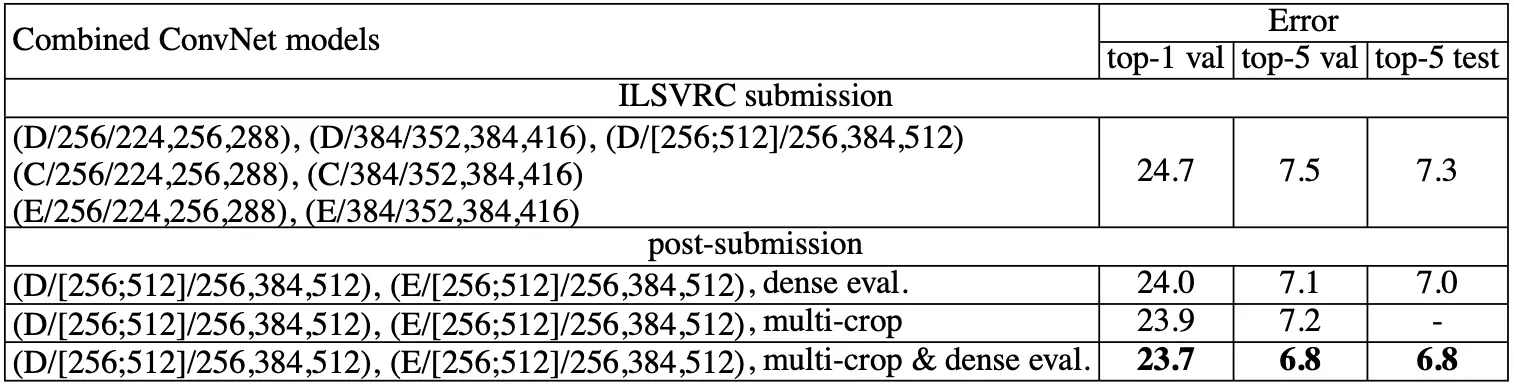
지금까지는 A~E 각각에 대한 Convolutional Network 의 성능을 평가했는데 비해서, 이 부분에서는 각 Convolutional Network 의 Softmax Layer 의 output 을 합치는 형태로 평가를 진행해본 결과를 알려줍니다. 이는 각 Convolutional Network 가 상호 보완적일 것으로 보고 진행한 것이라고 합니다. 결과는 아래의 표에 나타난 것과 같습니다.

위 표의 ILSVRC submission 은 7 개의 Convolutional Network 의 output 을 합친 결과를 바탕으로 평가를 진행한 것입니다. 그 결과 top-5 test 에서 7.3 % 를 얻었다고 합니다. (이 부분은 위의 Convolutional Network 의 top-5 test error 를 나타내 주지 않아서 비교는 불가능하지만, 논문에 제시한 것을 보면 성능이 높아졌다고 예상해봅니다)

이후 ILSVRC submission 이후에 가장 좋았던 D 와 E 를 각각의 evaluation method 에 맞게 두 개씩 합친 결과를 산출해보니 top-5 error 를 6.8% 까지 줄일 수 있었다고 합니다.

Comparison with State of the Art

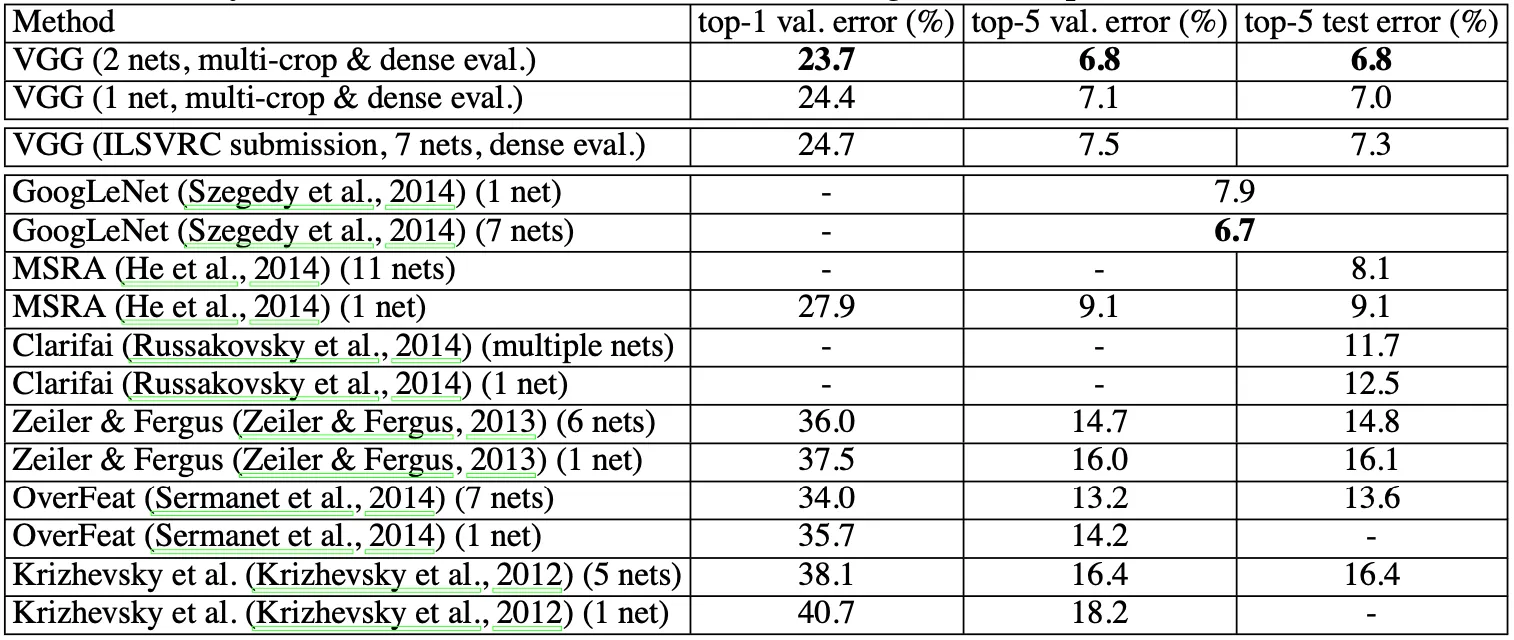
마지막으로, 논문에서는 State of the Art 연구들과 VGGNet 의 성능을 ILSVRC-2014 dataset 에 대해서 비교해줍니다.

그 결과 VGGNet 은 GoogLeNet 의 바로 아래인 2nd place 를 차지했고, ILSVRC-2012, 2013 에서 우승을 차지한 연구들에 비해서 큰 개선을 보여주었습니다. GoogLeNet 과도 0.1% 의 top-5 test error 차이만을 보이면서 경쟁적인 위치에 있다는 것을 보여주었고, 특히 1-Net 만을 따로 보았을 때는 오히려 VGGNet(7.0%) 이 1st place 를 차지하여 GoogLeNet(7.9%) 보다 0.9% 낮은 top-5 test error 를 보여주었습니다. 더욱이, VGGNet 은 고전 Convolutional Network 인 LeCun et al. 에 비해서 크게 다르지 않고 depth 만 증가시켰다는 점에서 의미가 있다고 말합니다.

Conclusion

이것으로 논문 “Very Deep Convolutional Networks for Large-Scale Image Recognition” 의 내용을 간단하게 요약해보았습니다.

최근에 딥러닝 관련 다양한 분야를 알기 위해서 다양한 논문들을 읽어왔는데, 그래도 제일 관심 있었던 Computer Vision 에서 그나마 유명하다고 불리는 친구들조차 읽지 않았어서 이번 기회에 한 번 읽어보았습니다. 논문에서 전달하는 바는 사실 작은 receptive field filter 여러 개를 사용하는 것이 효과적이라는 것인데, 그것에 비해서 testing 부분의 설명이 조금 어려웠던 것 같습니다. (특히 dense evaluation 부분이 저는 설명이 불친절해서 한참을 해맸던 것 같습니다)

생각보다는 간단하면서도 완벽히 이해하기는 어려웠던 논문이었던 것 같습니다. Computer Vision 에 관심이 있는 분은 꼭 읽어보시면 좋을 것 같습니다.