Duplicate

CV_HW4

마감일
2022/11/23
제출자
전기정보공학부 2017-12433 김현우

Question 1: Epipolar Geometry

Consider two images I1I_1 and I2I_2 that have been captured by a system of two cameras, and suppose the fundamental matrix of two images FF is known (note that the matrix FF satisfies the equation x2⊤Fx1=0{\rm \bf x}_2^\top F {\rm \bf x}_1=0 for any correspondence two pixel points (x1,x2)({\rm \bf x_1, x_2}) between images I1I_1 and I2I_2). And the epipoles are e1{\rm \bf e_1}and e2{\rm \bf e_2}. Answer the following questions.
a.
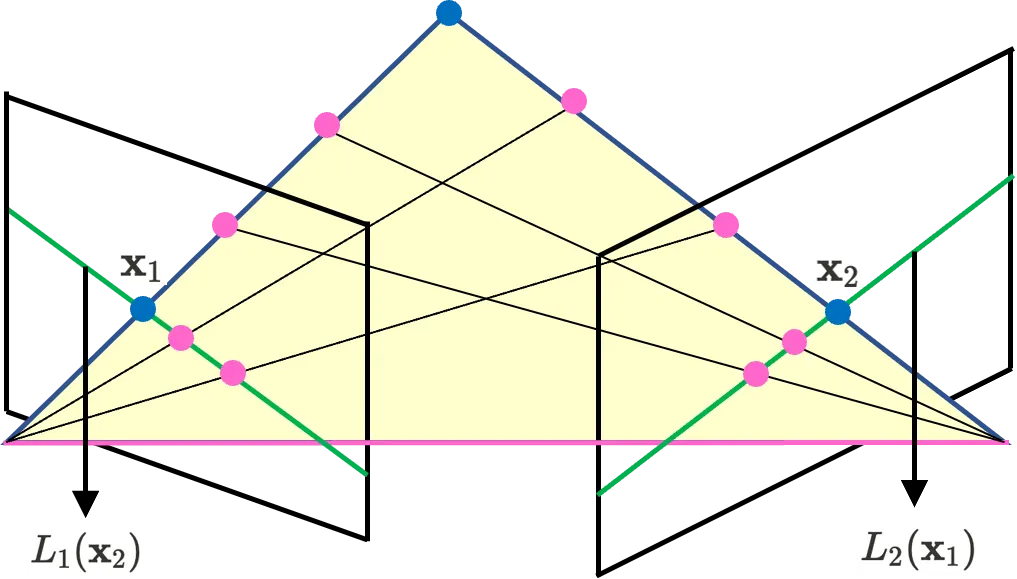
(4 points) Let L1(x2)={x1∣x2⊤Fx1=0}L_1({\rm \bf x}_2) = \{ {\rm \bf x}_1 |{\rm \bf x}_2^\top F {\rm \bf x}_1 = 0\} and L2(x1)={x2∣x2⊤Fx1=0}L_2({\rm \bf x}_1)=\{{\rm \bf x}_2|{\rm \bf x}^\top_2 F {\rm \bf x}_1 = 0\}, what doL1(x2)L_1({\rm \bf x}_2) and L2(x1)L_2({\rm \bf x}_1) look like? Draw the figures.
Without loss of generality, let’s consider only L1(x2)={x1∣x2⊤Fx1=0}L_1({\rm \bf x}_2) = \{ {\rm \bf x}_1 |{\rm \bf x}_2^\top F {\rm \bf x}_1 = 0\}, and set x2⊤F=[αβγ]{\rm \textbf x_2}^\top F = \begin{bmatrix} \alpha & \beta & \gamma \end{bmatrix}. For arbitrary points [xyf]\begin{bmatrix} x \\ y \\ f \end{bmatrix} on image plane I1I_1 which ff is an effective focal length, the equation changes as below.
[αβγ][xyf]=0→αx+βy+γf=0\begin{bmatrix} \alpha & \beta & \gamma \end{bmatrix} \begin{bmatrix} x \\ y \\ f \end{bmatrix} = 0 \rarr \alpha x + \beta y + \gamma f = 0
Since we consider the points on image plane, we can consider ff as constant and the equation becomes the format of line (y=−αβx−γfy=-\frac{\alpha}{\beta}x - \gamma f).
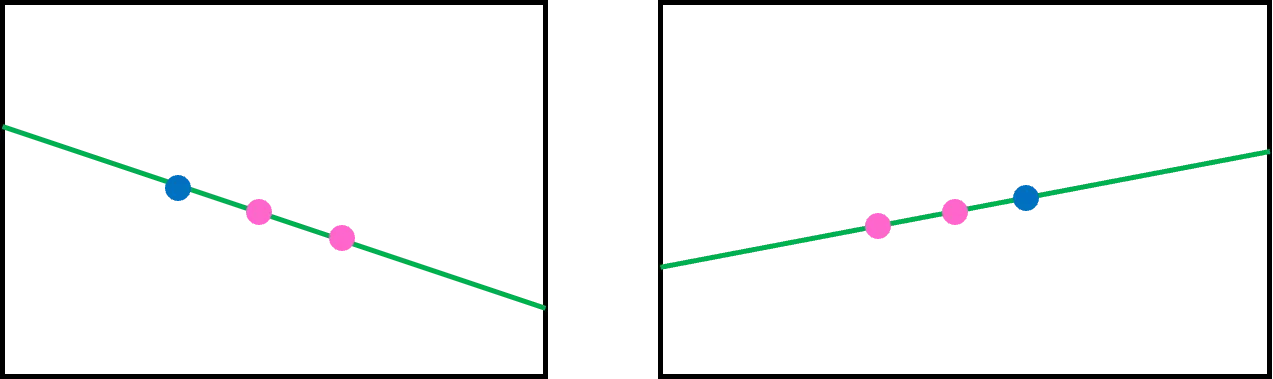
Therefore, both L1(x2)={x1∣x2⊤Fx1=0}L_1({\rm \bf x}_2) = \{ {\rm \bf x}_1 |{\rm \bf x}_2^\top F {\rm \bf x}_1 = 0\} and L2(x1)={x1∣x2⊤Fx1=0}L_2({\rm \bf x}_1)=\{{\rm \bf x}_1|{\rm \bf x}^\top_2 F {\rm \bf x}_1 = 0\} look like a green line on image plane as below.
The blue point on left side is x1{\rm \textbf x_1} on image plane I1I_1 and the blue point on right side is x2{\rm \textbf x_2} on image plane I2I_2. The blue point in middle is the exact 3D position which is corresponding to x1{\rm \textbf x_1} and x2{\rm \textbf x_2}. The green line on left image plane I1I_1 is L1(x2)L_1({\rm \textbf x_2}) and the green line on right image plane I2I_2 is L2(x1)L_2({\rm \textbf x_1}).
The view on each camera is such as below.
b.
(3 points) Derive det(F)=0{\rm det}(F) = 0.
Remind that every epipolar lines pass through epipole.
For all x1∈I1{\rm \textbf x_1} \in I_1, L2(x1)={x2∣x2⊤Fx1=0}L_2({\rm \bf x}_1)=\{{\rm \bf x}_2|{\rm \bf x}^\top_2 F {\rm \bf x}_1 = 0\} is epipolar line on I2I_2 which includes epipole e2{\rm \textbf e_2} (e2∈L2(x1){\rm \textbf e_2} \in L_2({\rm \bf x}_1)). Therefore, the below equation is satisfied.
e2⊤Fx1=0,∀x1∈I1\begin{equation} {\rm \bf e}^\top_2 F {\rm \bf x}_1 = 0, \quad \forall {\rm \textbf x_1} \in I_1 \end{equation}
Then, we can apply transpose on each side of the equation to form the equation as below.
x1⊤F⊤e2=0,∀x1∈I1\begin{equation} {\rm \bf x}^\top_1 F^\top {\rm \bf e}_2 = 0, \quad \forall {\rm \textbf x_1} \in I_1 \end{equation}
Let’s focus on F⊤e2F^\top {\rm \bf e}_2 term and assume F⊤e2≠0∈R3F^\top {\rm \bf e}_2 \ne 0 \in \mathbb R^3.
Then for F⊤e2=[a1a2a3]F^\top {\rm \bf e}_2 = \begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix} and x1⊤=[x1x2x3]{\rm \textbf x_1}^\top = \begin{bmatrix} x_1 & x_2 & x_3 \end{bmatrix}, a1x1=a2x2=a3x3=0a_1x_1 = a_2x_2 = a_3x_3 = 0 should be satsified by equation (2)(2). Since x1{\rm \textbf x_1} is expressed as homogeneous coordinate and on image plane I1I_1, x3≠0x_3 \ne 0 to prevent image plane on infinite. Thus, a3a_3 must be 0. Then there one or more values in a1,a2a_1, a_2 must be nonzero by assumption.
Without loss of generality, let’s consider the case of a1≠0a_1 \ne 0. Then we can consider x′=[x1′x2′x3′]∈I1{\rm \textbf x'} = \begin{bmatrix} x'_1 \\ x'_2 \\ x'_3 \end{bmatrix}\in I_1 which sastisfies a1x1′=a2x2′=a3x3′=0a_1x'_1 = a_2x'_2 = a_3x'_3 = 0. Then we can consider x′′=[x1′+ϵx2′x3′]∈I1{\rm \textbf x''} = \begin{bmatrix} x'_1 + \epsilon \\ x'_2 \\ x'_3 \end{bmatrix} \in I_1, the right side pixel of the x′{\rm \textbf x}' (ϵ≠0\epsilon \ne 0). For x′′{\rm \textbf x''}, we can calculate the first element of x′′⊤F⊤e2{\rm \bf x}''^\top F^\top {\rm \bf e}_2 as a1(x1′+ϵ)=a1x1′+a1=0+a1ϵ=a1ϵ≠0a_1(x_1' +\epsilon) = a_1x_1' + a_1 = 0 + a_1\epsilon = a_1\epsilon \ne 0. This contradicts with equation (2)(2).
Thus the assumption F⊤e2≠0∈R3F^\top {\rm \bf e}_2 \ne 0 \in \mathbb R^3 is wrong and we can safely say that F⊤e2=0F^\top {\rm \bf e}_2 = 0. Since the homogeneous coordinate doesn’t defined on (0,0,0)(0, 0, 0), e2≠[000]{\rm \textbf e_2} \ne \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} and this means that F⊤F^\top has nonzero vector e2{\rm \textbf e_2} which satisfies F⊤e2=0F^\top {\rm \textbf e_2} = 0, has non-zero nullity which means non-invertible and det(F⊤)=0{\rm det}(F^\top) = 0. Thus we can say det(F)=0{\rm det}(F) = 0 since determinant of transpose matrix is same as the determinant of original matrix.
c.
(3 points) In general, FF is unknown. Explain the 8-points algorithm to obtain FF with some
correspondence two pixel points
The 8-points algorithm is method for finding unkown fundamental matrix. For one pair of points pi=(ui,vi,1), pi′=(ui′,vi′,1)p_i = (u_i, v_i, 1),\ p_i'= (u_i', v_i' , 1), we can apply epipolar constarint as below.
pi′Fpi=0p_i'Fp_i = 0
If we set F=[F11F12F13F21F22F23F31F32F33]F = \begin{bmatrix} F_{11} & F_{12} & F_{13} \\ F_{21} & F_{22} & F_{23} \\ F_{31} & F_{32} & F_{33} \\ \end{bmatrix}, we can simplify the constraint as below.
[ui′vi′1][F11F12F13F21F22F23F31F32F33][uivi1]=0\begin{bmatrix} u_i' & v_i' & 1 \end{bmatrix} \begin{bmatrix} F_{11} & F_{12} & F_{13} \\ F_{21} & F_{22} & F_{23} \\ F_{31} & F_{32} & F_{33} \\ \end{bmatrix} \begin{bmatrix} u_i \\ v_i \\ 1 \end{bmatrix} = 0
We can expand the above equation as below.
F11ui′ui+F21vi′ui+F31ui+F12ui′vi+F22vi′vi+F32vi+F13ui′+F23vi′+F33=0\begin{align*} F_{11}u_i'u_i + F_{21}v_i'u_i + F_{31}u_i + F_{12}u_i'v_i + F_{22}v_i'v_i + F_{32}v_i + F_{13}u_i' + F_{23}v_i' + F_{33} = 0 \end{align*}
Finally, we can modify the equation as matrix multiplication of known terms with unknown FijF_{ij} term as one column vector.
[ui′uiui′viui′vi′uivi′vivi′uivi1][F11F12F13F21F22F23F31F32F33]=0\begin{bmatrix} u_i'u_i & u_i'v_i & u_i' & v_i'u_i & v_i'v_i & v_i' & u_i & v_i & 1 \end{bmatrix} \begin{bmatrix} F_{11} \\ F_{12} \\ F_{13} \\ F_{21} \\ F_{22} \\ F_{23} \\ F_{31} \\ F_{32} \\ F_{33} \\ \end{bmatrix} = 0
Since the column vector which consisted of the element of FF has 9 DoF and it is up to scale, we need 8 corresponding point pairs to construct Uf=0Uf = 0 (UU is 8×98\times 9 maxtrix, ff is above column vector consisted of FF terms) form to find ff.
As we’ve done in homography, we can solve above problem by setting the objective as below.
arg min⁡f∥Uf∥2  subject  to  ∥f∥2=1\argmin_f \|Uf \|^2 \thickspace \rm subject\thickspace to \thickspace\|f\|^2 =1
We can apply lagrange multiplier to find the minimum as below.
L(f)=∥Uf∥2−λ′(f⊤f−1)=f⊤U⊤Uf−λ′(f⊤f−1)L(f) =\|Uf\|^2 - \lambda'(f^\top f-1) = f^\top U^\top Uf - \lambda'(f^\top f-1)
If we differentiate above equation by ff to find minimum,
2U⊤Uf−λ′f=0→U⊤Uf=12λ′f2U^\top Uf-\lambda' f =0 \rarr U^\top Uf = \frac{1}{2}\lambda' f
we can figure out the minimum value occurs when ff is an eigenvector of U⊤UU^\top U. Then the corresponding value of our objective changes as below.
∥Uf∥2=f⊤(U⊤Uf)=f⊤λf=λ(f⊤f)=λ∥f∥2\|Uf\|^2 = f^\top (U^\top Uf) = f^\top \lambda f = \lambda (f^\top f) = \lambda\|f\|^2
To minimize above equation, we have to set λ\lambda as minimum value, thus we have to take ff as an eigenvector of U⊤UU^\top U which has minimum corresponding eigenvalue (including zero). By this way we can find out ff which consisted of the element of fundamental matrix FF, and we can reconstruct FF using ff.

Question 2: Depth Estimation from Stereo

In the lectures, we discussed depth estimation from stereo images. We can estimate the depth from the disparity of the corresponding points on two rectified images. We will explore one of the simple algorithms, window-based corresponding stereo matching by Sum-of-Squared Differences measures (SSD). In this question, there are both theory and programming problems. You should answer the all problems and implement the functions in disparity_ssd.py{\rm disparity\_ssd.py}.
a.
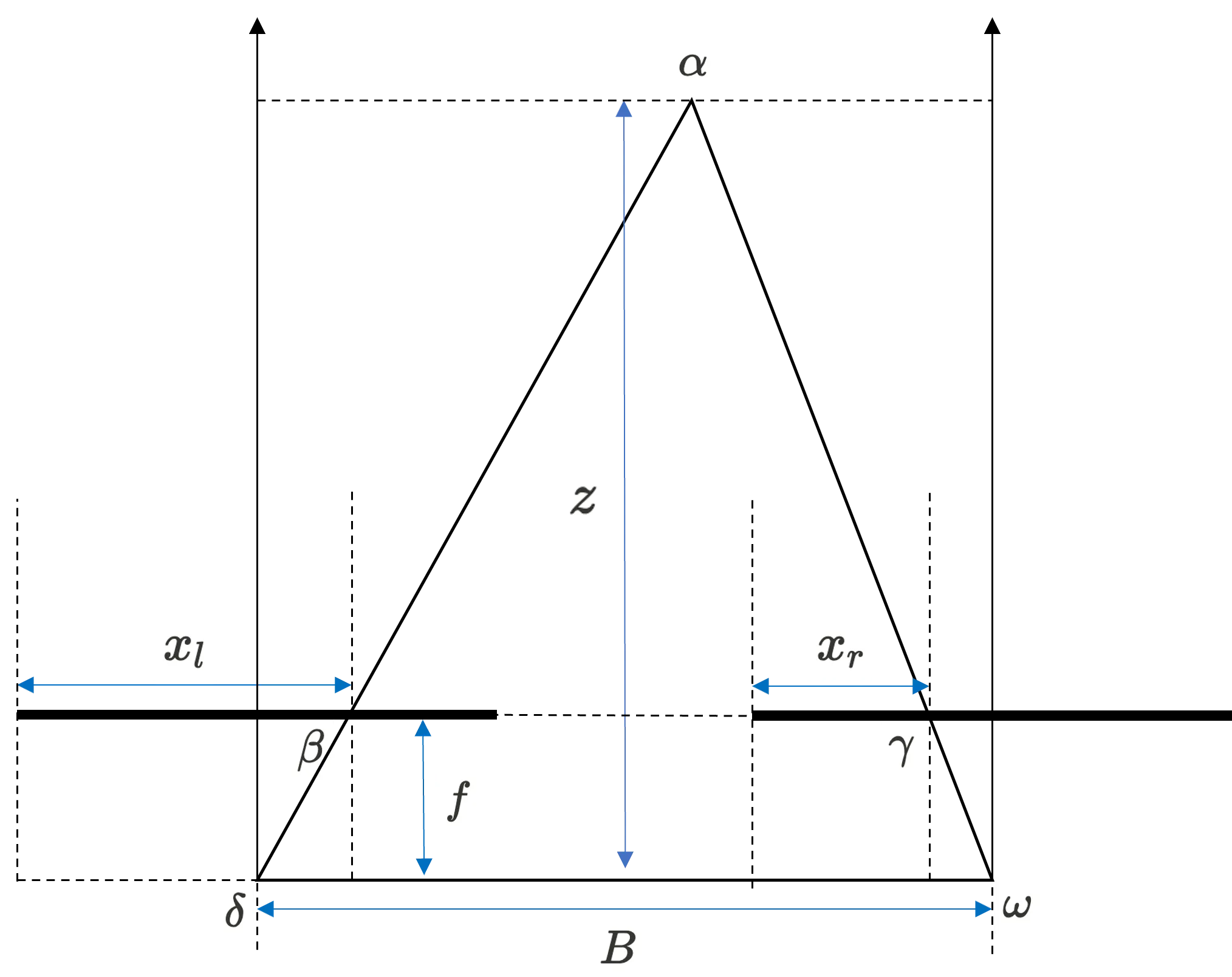
(3 points) Derive the depth zz of the point, which is defined by the distance from baseline, in terms of BB, dlrd_{lr}, ff (where BB is the distance between two optical centers, dlrd_{lr} is the disparity of two corresponding points, and ff is the effective focal length). Let’s consider the system with two cameras which have parallel opical axis as below.
Then, we can find triangle △αβγ\triangle \alpha\beta\gamma and △αδω\triangle\alpha\delta\omega is similar. Thus, we can say the height bootom line ratio of two triangle is same as below. (let aa as half width of image plane)
zB=z−fB+2a−xl−(2a−xr)=z−fB−(xl−xr)=z−fB−dlr\frac{z}{B} = \frac{z-f}{B + 2a - x_l - (2a-x_r)} = \frac{z-f}{B-(x_l-x_r)} = \frac{z-f}{B-d_{lr}}
Thus, we can compute depth zz as below.
z=fBdlrz = f\frac{B}{d_{lr}}
Let the rectified images be ILI_L and IRI_R, and the window size be ω\omega (practically set to odd number). The naive SSD matching algorithm is defined by Algorithm 1.
b.
(4 points) The above naive SSD matching algorithm has some problems. Explain why it is wrong in terms of epipolar geometry, and also explain how to fix it. According to epipolar geometry, we can find the corresponding points on the epipolar line. Then, we have to calculate SSD for all point patches whose center is on the line and this is time-consuming. To deal with this problem, we can set the set the system’s baseline relatively small enough to ensure the corresponding points on I2I_2 exists quite near to the original pixel on I1I_1 we want to find the pair. By applying this setting, we can assume there exists corresponding points near the original pixel.
c.
(12 points) Now, we’re going to implement your fixed SSD matching algorithm discussed on (b). Complete following functions, and then apply them to the given image pair L1.png and R1.png.
ssd=SSD(t,x,r,c,w),D=disparity_SSD_c(img1,img2){\rm ssd = SSD(t, x, r,c,w)}, \quad {\rm D=disparity\_SSD\_c(img1, img2)}
And also, display the disparity map using save_disparity_map(D){\rm save\_disparity\_map(D)} function (already implemented), and save it as results/disparity_c_L1R1.png{\rm results/disparity\_c\_L1R1.png}. Discuss the results in your writeup.
I firstly implement the function ssd=SSD(t,x,r,c,w){\rm ssd = SSD(t, x, r,c,w)} which outputs the sum of the square errors of patch t\rm t and patch around (r,c)\rm (r,c) of image xx with patch size of (w×w)\rm (w\times w).
Then, for implementing the function D=disparity_SSD_c(img1,img2){\rm D=disparity\_SSD\_c(img1, img2)}, I firstly padded two images to safely compute SSD\rm SSD by w0=w//2\rm w_0 =w //2 for top, bottom, left, and right.
Then, I assume that L1L1 is the image obtained from right-shifted camera compared to the camera which took L2L2. Thus, when I iterate over L1L1 pixels and try to find the corresponding matches on the same horizontal line on L2L2, I only focused on left pixels to find the match. Also I used max_disparity{\rm max\_disparity} parameter to simplify the problem to only find matches inside the range of [−max_disparity,0][-{\rm max\_disparity},0] difference between original pixel.
While iterating over pixels on L1L1, I save the pixel displacement between original focusing pixel (which I iterating over) and the maximum SSD{\rm SSD} showing pixel on L2L2 to construct matrix DD and return it
Visualization of image L1L1 and matrix DD is as below.
Image L1
disparity_SSD_c(L1, R1)
We can figure out that the bright pixels are nearer (in perspective of zz direction, depth) than dark pixel which is
d.
(6 points) Apply the algorithm you implemented on (c)(c) to L1.png{\rm L1.png} and R2.png{\rm R2.png}. and save it as results/disparity_c_L1R2.png{\rm results/disparity\_c\_L1R2.png}. Also, compare the result and explain why it fails. Can you improve your SSD algorithm to mitigate this issue? Complete the function
D=disparity_SSD_d(img1,img2){\rm D = disparity\_SSD\_d(img1, img2)}
Apply this to two pairs (L1,R1)({\rm L1, R1}) and (L1,R2)({\rm L1, R2}) again, and save each of them as 3
results/disparity_d_L1R1.png{\rm results/disparity\_d\_L1R1.png} and results/disparity_d_L1R2.png{\rm results/disparity\_d\_L1R2.png}
If there isn’t brightness consistancy on two images, I could check the SSD{\rm SSD}-based implementation failes to estimate depth as below.
disparity_SSD_c(L1, R2)
Thus, I implement new algorithm disparity_SSD_d{\rm disparity\_SSD\_d} intuited by normalized cross correlation. Since there might be wrong match when the image scale is different in general matching problem, we could use normalized cross correlation. In this case, I used normalized SSD, which normalize two patch region with L2 norm, and then compute SSD.
disparity_SSD_d(L1, R1)
disparity_SSD_d(L1, R2)
As shown in above images, I could successfully find the depth map using normalized SSD.

Question 3: Motion and Optical Flow (20 points)

a.
(4 points) Give an example of a sequence of images from which you could not recover either horizontal or vertical components of motion. Explain in terms of number of knowns and unknowns of the optical flow equation.
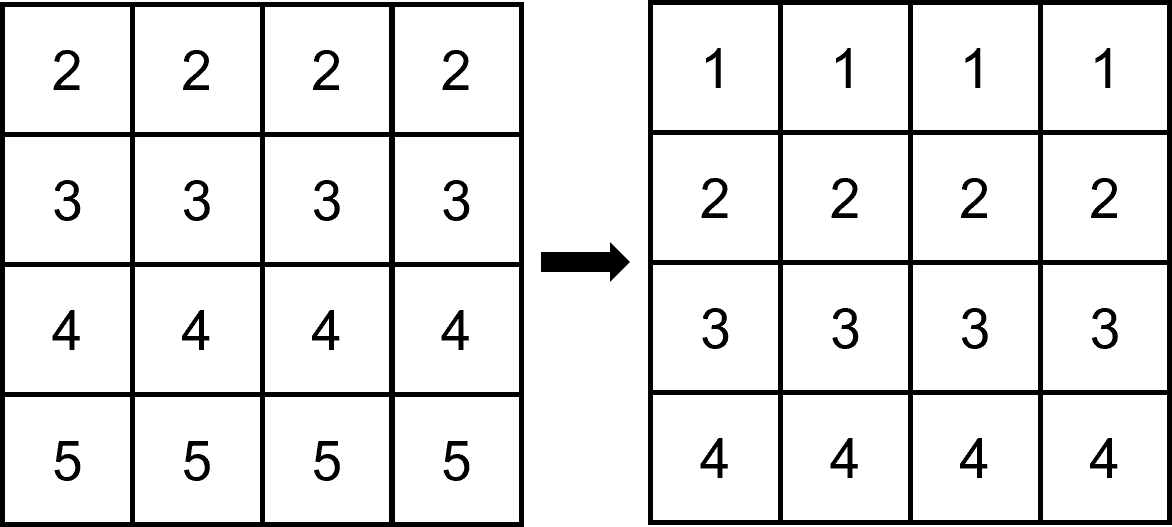
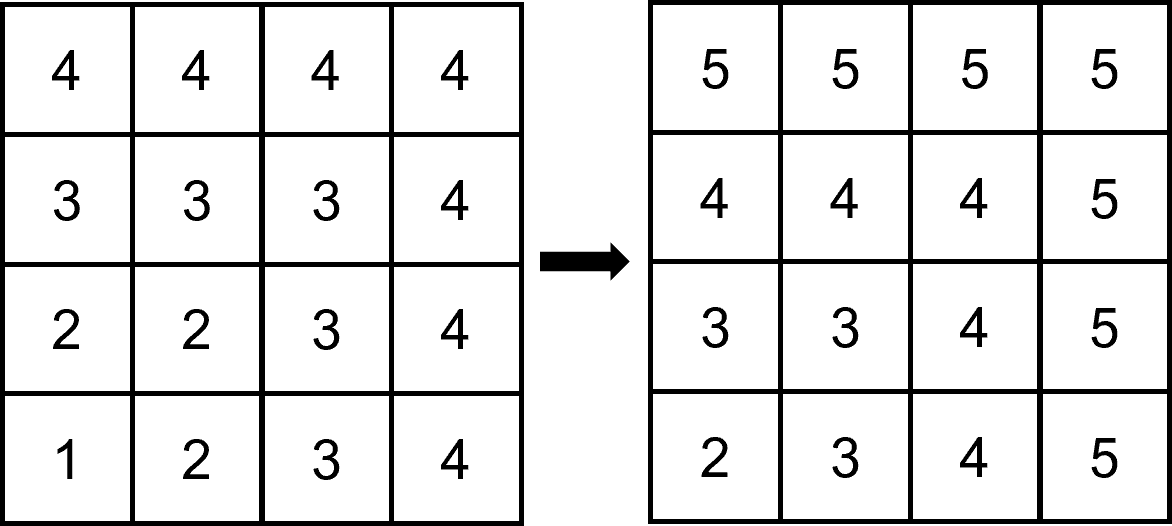
Below figure is an example of sequences of images we could not recover horizontal component of motion. (Each number is pixel intensity)
Consider optical flow eqation Ixu+Iyv+It=0I_xu+I_yv +I_t = 0.
For point (3,3)(3,3), we can figure out Ix(3,3)=0I_x(3,3) =0, Iy(3,3)=1I_y(3,3)=1, It(3,3)=−1I_t(3,3)=-1. Thus, we can construct optical flow equation as below. (We define left, up most pixel is (1,1)(1,1) and right, down direction increases each x,yx, y coordinates)
v−1=0v - 1 = 0
Thus, we can figure out v=1v=1.
However, for other points, we can only construct same optical flow equation as above. Therefore we cannot know about the information of uu. (For two unknowns uu and vv, we cannot figure out one unknown uu)
b.
(4 points) Give an example of a sequence of images from which you could always recover horizontal or vertical components of motion. As in (a)(a), explain with regards to knowns and unknowns.
Below figure is an example of sequences of images we could always recover vertical component of motion. (Each number is pixel intensity)
Consider optical flow eqation Ixu+Iyv+It=0I_xu+I_yv +I_t = 0.
For point (3,3)(3,3), we can figure out Ix(3,3)=1I_x(3,3) =1, Iy(3,3)=0I_y(3,3) = 0, It(3,3)=1I_t(3,3) = 1. Then we can construct optical flow equation as below. (We define left, up most pixel is (1,1)(1,1) and right, down direction increases each x,yx, y coordinates)
u+1=0u + 1 = 0
For point (2,2)(2,2), we can figure out Ix(2,2)=0I_x(2,2) =0, Iy(3,3)=−1I_y(3,3) = -1, It(3,3)=1I_t(3,3) = 1. Then we can construct optical flow equation as below. (We define left, up most pixel is (1,1)(1,1) and right, down direction increases each x,yx, y coordinates)
−v+1=0-v+1 = 0
Thus, we can figure out both uu and vv as u=−1u = -1 and v=1v = 1. (left & down direction) (For two unknowns uu and vv, we can figure out both of them.)
c.
(6 points) Consider a situation where the motion of the camera is in the forward direction. Does the optical flow equation still hold? Find a simple way to figure out which scene point the object is moving towards.
While the key assumptions of optical flow equation (brightness consistency & small motion) is holded, the optical flow equation can be still applied on the situation since it is pixel-based method.
However, when camera is moving in the forward direction, the object displayed on image get’s larger and the corresponding region are also expanded. This means that it is hard to easily match the exact region (or pixel) of correspondence. In this situation the brightness consistency cannot be fully applied.
Also, the mapping of 3D point to 2D image plane (x,y,z)→(x′,y′)(x,y,z) \rarr (x',y') has the relationship of x′=fxz,y′=fyzx' = f\frac{x}{z}, y' = f\frac{y}{z} and if depth zz becomes smaller (close to the camera), the same amount of the zz changes Δz\Delta z makes more and more large amount of changes of Δx′\Delta x' and Δy′\Delta y'. This means, after the particular timing when object is close enough to camera, the small motion assumption can be not fully applied since Δz\Delta z occured by small Δt\Delta t can make large pixel difference.
Thus in general, we cannot say the optical flow equation hold in the situation given.
To figure out which scene point the object is moving towards, we can use depth information and prior knowledge of still objects (such as trees, buildings). By using the still objects (prior knowledge) depth changes in sequence of images, we can compute the camera velocity. Also, we can compute the zz direction velocity of scene point using depth changes. If the scene point velocity towards camera direction is larger than camera velocity, we can say the scene point is moving towards camera. If it is similar with camera velocity, we can say the scene point is still. (We can also use camera velocity directly if it is given, instead of prior knowledge of still objects.)
d.
(6 points) Consider a camera observing a 3D scene in which each point has the same translation motion. This means the velocity at each point has the same components. Show that all the optical flow vectors originate from the same point on the image plane. This point is called the focus of expansion. Consider random scene point (xt,yt,zt)(x_t,y_t,z_t) in time tt which showing constant translation motion vx=dxdtv_x = \frac{dx}{dt}, vy=dydtv_y = \frac{dy}{dt}, vz=dzdtv_z = \frac{dz}{dt}. Then we know the corresponding points on image plane is shown as below.
xt′=fxtzt,yt′=fytztx_t' = f\frac{x_t}{z_t}, \quad y_t' = f\frac{y_t}{z_t}
Let’s consider Δt\Delta t time after situation. Then, the scene point changed to be (xt+vxΔt,yt+vyΔt,zt+vzΔt)(x_t+v_x\Delta t, y_t+v_y\Delta t, z_t+v_z\Delta t). We can also know the corresponding points on image plane as below.
xt+Δt′=fxt+vxΔtzt+vzΔt,yt+Δt′=fyt+vyΔtzt+vzΔtx_{t+\Delta t}' = f\frac{x_t + v_x \Delta t}{z_t + v_z \Delta t}, \quad y_{t+\Delta t}' = f\frac{y_t + v_y \Delta t}{z_t + v_z \Delta t}
Consider the original position of the scene point displayed on image plane. We can compute the position by considering Δx→−∞\Delta x \rarr -\infty.
x−∞′=fvxvz,y−∞′=fvyvzx_{-\infty}' = f\frac{v_x}{v_z }, \quad y_{-\infty}' = f\frac{v_y}{ v_z}
The above position is the original rendered position of random 3D scene point having constant translation motion. We can know that the position is unrelated to the specific position of 3D scene point. Thus we can show that all the optical flow vectors originate from the same point on the image plane.

Question 4: Lucas-Kanade Method (45 points)

In this section, you will implement a tracker for estimating dominant affine motion in a sequence of images, and subsequently identify pixels corresponding to moving objects in the scene. You will be using the images in the directory data/motion{\rm data/motion}, which consists aerial views of moving objects from a non-stationary camera.
4.1. Dominant Motion Estimation
To estimate dominant motion, the entire image I(t)I(t) will serve as the template to be tracked in image I(t+1)I(t+1), i.e.{\rm i.e.} I(t)I(t) is assumed to be approximately an affine warped version of I(t+1)I(t+1). This approach is reasonable under the assumption that a majority of the pixels correspond to stationary objects in the scene whose depth variation is small relative to their distance from the camera. Using the affine flow equations, you can recover the 6-vector p=[p1 p2 p3 p4 p5 p6]Tp= [ p_1\ p_2\ p_3\ p_4\ p_5\ p_6 ]^T of affine flow parameters. They relate to the equivalent affine transformation matrix as:
M=[1+p1p3p5p21+p4p6001] M= \begin{bmatrix} 1+p_1 & p_3 & p_5 \\ p_2 & 1+p_4 & p_6 \\ 0 & 0 & 1 \end{bmatrix}
relating the homogenous image coordinates of I(t)I(t) to I(t+1)I(t+1) according to xt=Mxt+1{\rm x_t}=M{\rm x_{t+1}} (where x=[x y 1]T{\rm x} = [x\ y\ 1]^T). For the next pair of consecutive images in the sequence, image I(t+2)I(t+2) will serve as the template to be tracked in image I(t+1)I(t+1), and so on through the rest of the sequence. Note that M will differ between successive image pairs.
Each update of the affine parameter vector, Δp\Delta p is computed via a least squares method using the pseudo-inverse as described in class. Note{\rm Note}: Image I(t)I(t) will almost always not be contained fully in the warped version of I(t+1)I(t+1). Hence the matrix of image derivatives and the temporal derivatives must be computed only on the pixels lying in the region common to I(t)I(t) and the warped version of I(t+1)I(t+1) to be meaningful.
For better results, Sobel opterators may be used for computing image gradients. So, we have provided a code for them.
a.
(35 points) Lucas-Kanade Method Complete the following function and explain your code in your writeup:
p=lucas_kanade_affine(T,I)p = {\rm lucas\_kanade\_affine(T, I)}
where T,I{\rm T, I} indicate I(t)I(t) and I(t+1)I(t+1), and p{\rm p} is the estimated affine parameter vector.
A naive implementation may not work well. Then, refer to the following tips:
•
This function will probably take too long. Then, try to subsample pixels when you compute the Hessian matrix HH and Δp\Delta p. Or, use numpy.einsum{\rm numpy.einsum} to calculate the sum-of-product two matrices efficiently.
In this implementation, I totally followed Lucas-Kanadde Algorithm.
First, I normalize my sobel operator result by dividing the gradient values by the sum of the sobel operator elements. This process ensure to keep the pixel scale same as before.
Then, I warp image I(t)I(t) to match on I(t+1)I(t+1) by applying WW on warped image’s coordinate and get corresponding pixel value of I(t)I(t). To access floating point pixel values in I(t)I(t), I use RectBivariateSpline(){\rm RectBivariateSpline}() rather than naive bilinear interpolation. By this process, I can get error image.
Then, I have to compute hessian, thus I first compute the term ∇I∂W∂p\nabla I \frac{\partial W}{\partial p} for all position (by using appropriate einsum{\rm einsum}) which has dimension of 6×(h×w)6\times (h\times w) where hh and ww is height and width of image I(t)I(t). To calculate hessian from this vector, I used matrix multiplication of the previous vector and transpose of it, to get 6×66\times 6 hessian matrix.
Finally, to compute Δp\Delta p, I have to multiply ∇I∂W∂p\nabla I \frac{\partial W}{\partial p} term with error image elemenwisely (in the term of position) and sum up the result to compute final 6×16\times 1 vector. Then I matrix multiply inverse hessian with the previous vector to finally get Δp\Delta p and add it to original pp and return the result.
4.2. Moving Object Detection
Once you are able to compute the transformation matrix MM relating an image pair I(t)I(t) and I(t+1)I(t+1), a naive way of determining pixels lying on moving objects is as follows. Warp the image I(t+1)I(t+1) using MM so that it is registered to I(t)I(t), and subtract it from I(t)I(t). The locations where the absolute difference exceeds a threshold can then be regarded as moving objects.
For better results, hysteresis thresholding may be used. So we have provided a code for hysteresis thresholding.
b.
(10 points) Dominant Motion Subtraction Complete the following function and explain your code in your writeup:
mask=subtract_dominant_motion(It,It1){\rm mask = subtract\_dominant\_motion(It,It1)}
where It{\rm It} and It1{\rm It1} indicate I(t)I(t) and I(t+1)I(t+1), and mask{\rm mask} is a binary 2D array of the same size that dictates which pixels are considered to be corresponding to moving objects. You should invoke lucas_kanade_affine{\rm lucas\_kanade\_affine} in this function to derive p{\rm p}, and produce the aforementioned binary mask accordingly.
To compute the motion image, I have to get appropriate warp defined by pp which can be computed by previous function lucas_kanade_affine(T,I){\rm lucas\_kanade\_affine(T, I)}. I call the function to get pp and defined warp function WW which maps coordinate xt+1{\rm x}_{t+1} to xt{\rm x}_{t}.
In the same way I discussed in 4.1, I can get warped image of I(t)I(t) to match I(t+1)I(t+1) using WW by using interpolation function RectBivariateSpline(){\rm RectBivariateSpline}(). Then, I can safely compute the motion of image by simply subtract the warped image of I(t)I(t) and I(t+1)I(t+1).