Duplicate

Lecture 13 | Triangulation + TK Factorization

수강 일자
2023/03/03

Triangulation

•
Calibration Parameters 를 아는 cameras 들을 이용해 3D Points 를 reconstuction 하는 과정.
◦
Calibration 은 Corresponding Point 들로 F{\rm F} 를 구한다음에 decomposition 하는 것이 일반적임.
◦
두 개 초과의 camera 를 사용하면 더 정확한 reconstruction 이 가능함.
•
정확하지 않은 대응점들에 기반한 Ray 는 서로 만나지 않을 수 있고, 이 경우 3D Point 를 정의하기 위해서는 2D 에 projection 한 점과 실제 점의 오차를 기반으로 정의되는 reprojection error 를 사용하여 최적화된 점을 찾을 수 있음.

Triangulation: Computing 3D Point (Algebraic)

x1=P1X=[p11Tp12Tp13T]X=[p11TXp12TXp13TX]{\rm x}_1 = {\rm P}_1{\rm X} = \begin{bmatrix} {{\rm p}_1^1}^T \\ {{\rm p}_1^2}^T \\ {{\rm p}_1^3}^T \\ \end{bmatrix}{\rm X} = \begin{bmatrix} {{\rm p}_1^1}^T{\rm X} \\ {{\rm p}_1^2}^T{\rm X} \\ {{\rm p}_1^3}^T{\rm X} \\ \end{bmatrix} \\
•
Multiview 로부터 3D Point 를 계산하는 Algebraic Solution
•
일반적인 3D → 2D projection 의 식은 위와 같음.
•
위 식은 Up-to-Scale 을 포함한 식이기 때문에 이를 제거한 Cross Product 형태로 바꿀 수 있음.
[x1y11]=x1≡P1X→[x1y11]×P1X=0\begin{bmatrix} x_1 \\ y_1 \\ 1 \end{bmatrix} ={\rm x}_1 \equiv {\rm P}_1{\rm X} \to \begin{bmatrix} x_1 \\ y_1 \\ 1 \end{bmatrix}\times {\rm P}_1{\rm X} = 0
•
DLT 를 사용하게 위해 풀어서 쓰면 다음과 같은 식들로 나눌 수 있음.
x1(p13TX)−p11TX=0y1(p13TX)−p12TX=0x1(p12TX)−y1p11TX=0x_1({p_1^3}^T{\rm X})-{p_1^1}^T{\rm X} = 0 \\ y_1({p_1^3}^T{\rm X})-{p_1^2}^T{\rm X} = 0 \\ x_1({p_1^2}^T{\rm X})-y_1{p_1^1}^T{\rm X} = 0 \\
•
위 세 번째 식은 사실 첫 번째 식과 두 번째 식으로 만들 수 있어서 (redundant) 사용하지 못하고, 다음과 같은 형태로 DLT 를 구축할 수 있음.
[x1(p13T)−p11Ty1(p13T)−p12T]X=0\begin{bmatrix} x_1({p_1^3}^T)-{p_1^1}^T \\ y_1({p_1^3}^T)-{p_1^2}^T \end{bmatrix}{\rm X} = 0
•
NN 개의 view 가 있다면 DLT 의 좌항에 총 2N2N 개의 row 가 추가되어 좌항은 2N×42N\times 4 matrix 가 됨.
•
이후 ∥AX∥\| A{\rm X} \| 의 최솟값을 구해 X{\rm X} 를 optimize 할 수 있음.

Triangulation: Computing 3D Point (Geometric)

X∗=arg min⁡x∑i∥πi(X)−xi∥22(Pi1XPi3X−xi)2−(Pi2XPi3X−yi)2{\rm X}^* = \argmin_{\rm x} \sum_i \| \pi_i({\rm X})-{\rm x}_i \|_2^2 \\ (\frac{{\rm P}_i^1{\rm X}}{{\rm P}_i^3{\rm X}}-x_i)^2 - (\frac{{\rm P}_i^2{\rm X}}{{\rm P}_i^3{\rm X}}-y_i)^2
•
Multiview 로부터 3D Point 를 계산하는 Geometric Solution
•
예측한 X{\rm X} 에서 다시 각 Camera 및 Image Plane 에 projection 하여 맺힌 점의 위치와 측정한 점의 위치의 차이를 최소화하는 방법임.
◦
πi\pi_i: Reprojected Point
◦
xi{\rm x}_i: Measured (Corresponding) Point
•
DLT 로 initialize 하고 optimization based method (e.g. gradient descent) 를 사용하여 최종적으로 해결함.

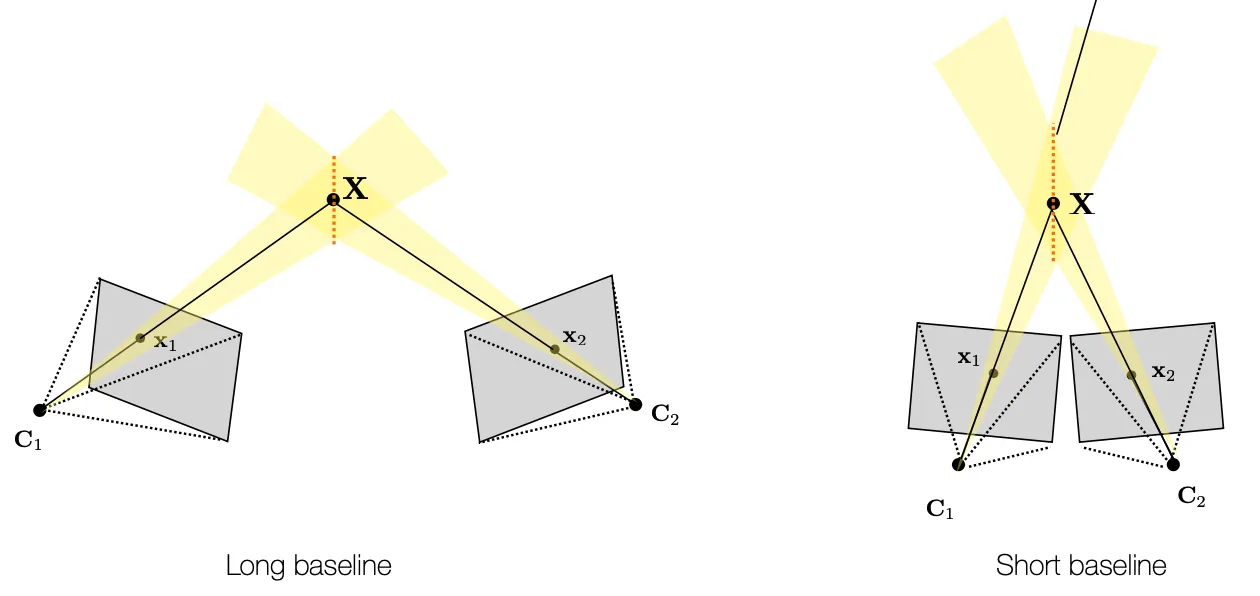
Traingulation Uncertainty

•
Long Baseline 을 가진 경우 Depth 방향 Uncertainty 가 작지만, Feature Matching (Finding Corresponding Points) 이 어려움.
•
Short Baseline 을 가진 경우 Depth 방향 Uncertainty 가 크지만, Feature Matching (Finding Corresponding Points) 이 쉬움.
•
선택에 대한 정답은 없고, camera 를 여러 개 쓰면 좋음. 다다익카

Structure-from-Motion: Tomasi-Kanade Factorization

•
Casual Video 나 Image 를 입력으로 받아 3D Scene Points 와 Camera Pose 를 출력하는 것
◦
Input: (xif,yif)(x_{if}, y_{if}), ii 는 feature point 의 index, ff 는 view 의 index
◦
Output: 3D Scene Point Xi{\rm X}_i
◦
Unknown: Camera Position Cf{\rm C}_f, Camera Orientation (uf,vf)({\rm u}_f, {\rm v}_f)
•
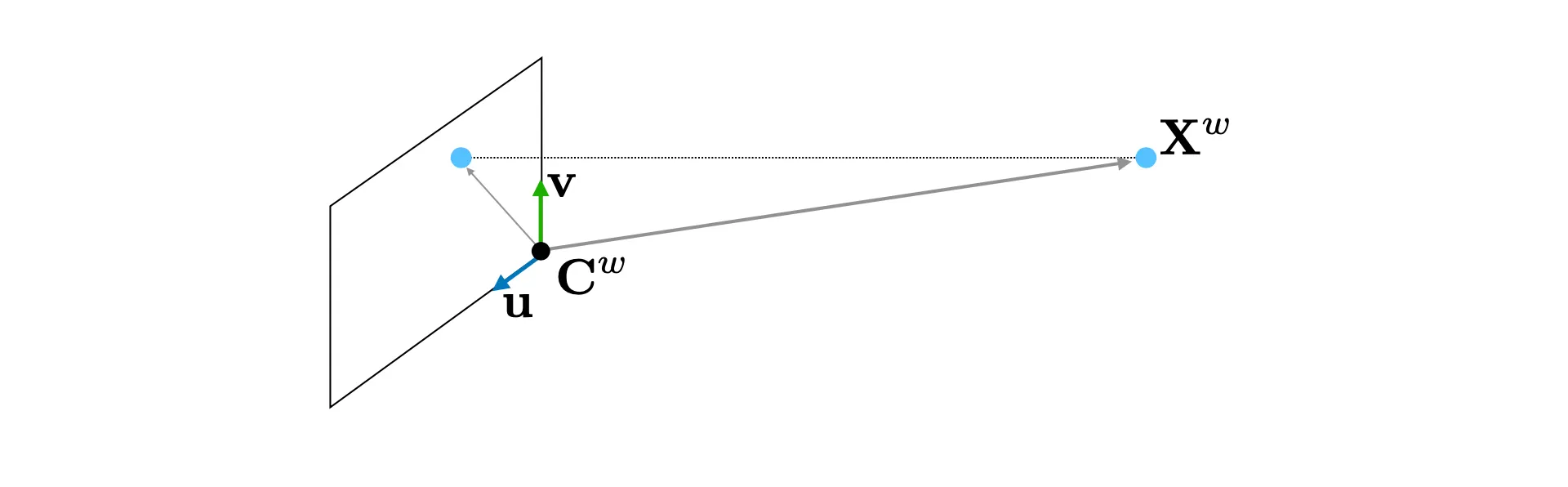
Orthographc Projection 을 가정으로 함.
x=uTXc=uT(Xw−Cw)y=vTXc=vT(Xw−Cw)x = {\rm u}^T{\rm X}^c = {\rm u}^T({\rm X}^w - {\rm C}^w) \\ y = {\rm v}^T{\rm X}^c = {\rm v}^T({\rm X}^w - {\rm C}^w) \\
◦
Xw{\rm X}^w: Real World 3D Point
◦
Cw{\rm C}^w: Camera Coordinate
◦
u,v\rm u, v: Image Plane x,yx, y direction
◦
Xc=Xw−Cw{\rm X}^c = {\rm X}^w - {\rm C}^w: Displacement from Camera Coordinate to Real World 3D Point
◦
더불어 World Coordinate 의 origin 을 3D point 의 중심점으로 두어, 모든 3D Point 를 더하면 0 이 되도록 가정할 수 있음.
1N∑iNXi=0\frac{1}{N}\sum_i^N X_i = 0
•
Centering Trick
x^if=xif−1N∑j=1Nxjf=xif−xˉfy^if=yif−1N∑j=1Nyjf=yif−yˉf\hat{x}_{if} = x_{if} - \frac{1}{N}\sum_{j=1}^Nx_{jf} = x_{if}-\bar{x}_f \\ \hat{y}_{if} = y_{if} - \frac{1}{N}\sum_{j=1}^Ny_{jf} = y_{if}-\bar{y}_f \\
◦
기본적인 이미지의 기준점은 Corner Point 이지만, 이 기준점을 Feature Point 의 중심점으로 옮겨 각 Feature Point 들을 모두 더하면 0 이 되도록 함.
◦
이렇게 하면, 2D Image 의 Projection Point 는 다음과 같이 간략화할 수 있음.
x^if=xif−1N∑j=1Nxjf=uT(Xi−Cf)−1N∑j=1Nxjf=uT(Xi−Cf)−1N∑j=1NuT(Xj−Cf)=uT(Xi−Cf)−uT1N∑j=1NXj+uTCf=uTXii.s.wy^if=vTXi\begin{align*} \hat{x}_{if} &= x_{if} - \frac{1}{N}\sum_{j=1}^Nx_{jf} \\ &= {\rm u}^T({\rm X}_i - {\rm C}_f) - \frac{1}{N}\sum_{j=1}^Nx_{jf} \\ &= {\rm u}^T({\rm X}_i - {\rm C}_f) - \frac{1}{N}\sum_{j=1}^N{\rm u}^T({\rm X}_j - {\rm C}_f) \\ &= {\rm u}^T({\rm X}_i - {\rm C}_f) - {\rm u}^T\frac{1}{N}\sum_{j=1}^N{\rm X}_j + {\rm u}^T{\rm C}_f \\ &= {\rm u}^T{\rm X}_i \\ {\rm i.s.w}\quad \hat{y}_{if} &= {\rm v}^T{\rm X}_i \end{align*}
▪
가운데 항은 가정에 의해서 0 이고 제일 끝항은 앞 항의 두 번쨰 항목과 상쇄되어 사라짐.
▪
이렇게 하면, Camera 항목이 Projection 에서 사라져버림.
•
결국 Corresponding Points 를 decompose 만 할 수 있다면 Camera Motion 과 3D Scene Point 를 찾을 수 있음.
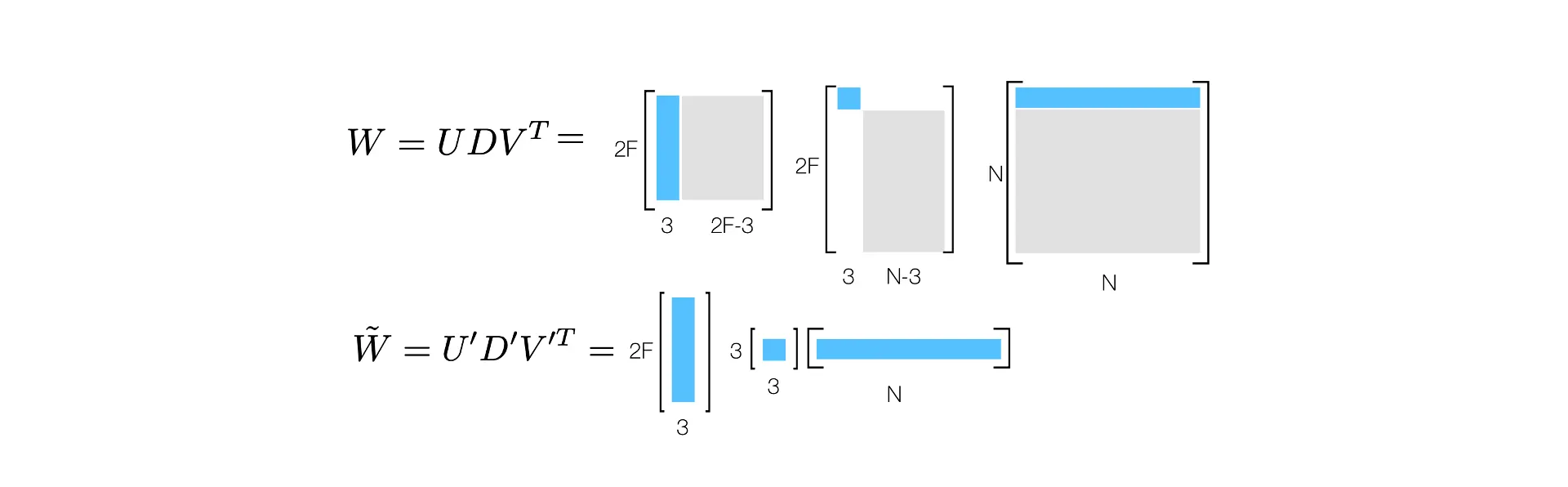
x^if=uTXiy^if=vTXi→[x^11x^21⋯x^N1x^11x^21⋯x^N1⋯⋯⋯⋯x^1Fx^2F⋯x^NFy^11y^21⋯y^N1y^11y^21⋯y^N1⋯⋯⋯⋯y^1Fy^2F⋯y^NF]=[u1Tu2T⋯uFTv1Tv2T⋯vFT][X1X2⋯XN]↔W2F×N=M2F×3S3×N\hat{x}_{if} = {\rm u}^T{\rm X}_i \\ \hat{y}_{if} = {\rm v}^T{\rm X}_i \\ \quad \\ \begin{align*} &\to \begin{bmatrix} \hat{x}_{11} & \hat{x}_{21} & \cdots & \hat{x}_{N1} \\ \hat{x}_{11} & \hat{x}_{21} & \cdots & \hat{x}_{N1} \\ \cdots & \cdots & \cdots & \cdots \\ \hat{x}_{1F} & \hat{x}_{2F} & \cdots & \hat{x}_{NF} \\ \hat{y}_{11} & \hat{y}_{21} & \cdots & \hat{y}_{N1} \\ \hat{y}_{11} & \hat{y}_{21} & \cdots & \hat{y}_{N1} \\ \cdots & \cdots & \cdots & \cdots \\ \hat{y}_{1F} & \hat{y}_{2F} & \cdots & \hat{y}_{NF} \\ \end{bmatrix} = \begin{bmatrix} {\rm u}_1^T \\ {\rm u}_2^T \\ \cdots \\ {\rm u}_F^T \\ {\rm v}_1^T \\ {\rm v}_2^T \\ \cdots \\ {\rm v}_F^T \\ \end{bmatrix} \begin{bmatrix} {\rm X}_1 & {\rm X}_2 & \cdots & {\rm X}_N \end{bmatrix} \\ &\lrarr W_{2F\times N} = M_{2F\times 3} S_{3\times N} \end{align*}
◦
WW 를 Observation Matrix 라고 부름.
◦
Rank(W)≤min⁡(Rank(M),Rank(S))=3{\rm Rank}(W) \le \min({\rm Rank}(M), {\rm Rank}(S))=3
•
WW 의 Rank 를 맞추기 위해 WW 에 SVD 를 적용하고 3개의 행, 열을 제외하고 다 0으로 바꾸어버릴 수 있음.
◦
이렇게 Rank 를 줄인 W~=U′D′V′T\tilde W = U'D'V'^T 로 정의할 수 있음.
•
Decomposition 을 위해서 다음과 같이 가운데 DD 를 반씩 쪼개서 나눌 수 있음.
U′D′V′T=(U′D′12)(D′12V′T)≃M2F×NS3×NU'D'V'^T = (U'D'^{\frac{1}{2}})(D'^{\frac{1}{2}}V'^T) \simeq M_{2F\times N}S_{3\times N}
◦
M2F×N=U′D′12M_{2F\times N} = U'D'^{\frac{1}{2}} 로, S3×N=D′12V′TS_{3\times N = }D'^{\frac{1}{2}}V'^T 로 단순하게 지정할 수 있음.
◦
하지만, 3×33\times 3 invertible matrix QQ 에 대해 M2F×N=U′D′12Q,S3×N=Q−1D′12V′TM_{2F\times N}= U'D'^{\frac{1}{2}}Q, S_{3\times N } = Q^{-1}D'^{\frac{1}{2}}V'^T 도 또 다른 해가 됨.
•
여러 가능성 중 하나를 선택하기 위해서 기존에 Camera Motion 의 Orthonormality Constraint 를 활용할 수 있음.
ufTuf=1vfTvf=1ufTvf=0{\rm u}_f^T{\rm u}_f =1 \\ {\rm v}_f^T{\rm v}_f =1 \\ {\rm u}_f^T{\rm v}_f =0 \\
◦
기존 M2F×N=U′D′12QM_{2F\times N} = U'D'^{\frac{1}{2}}Q 를 다음과 같이 나타낼 수 있음.
U′D′12Q=[u~1Tu~2T⋯u~FTv~1Tv~2T⋯v~FT]QU'D'^{\frac{1}{2}} Q = \begin{bmatrix} \tilde {\rm u}_1^T\\ \tilde {\rm u}_2^T \\ \cdots \\ \tilde {\rm u}_F^T \\ \tilde {\rm v}_1^T \\ \tilde {\rm v}_2^T \\ \cdots \\ \tilde {\rm v}_F^T \\ \end{bmatrix}Q
◦
위와 같은 세팅에서 기존의 Orthonormality Constraint 는 다음과 같이 변환할 수 있음.
u~fTQQTu~f=1v~fTQQTv~f=1u~fTQQTv~f=0\tilde{\rm u}_f^T QQ^T \tilde{\rm u}_f = 1 \\ \tilde{\rm v}_f^T QQ^T \tilde{\rm v}_f = 1 \\ \tilde{\rm u}_f^T QQ^T \tilde{\rm v}_f = 0 \\
◦
위 식에서 QQTQQ^T 는 DLT 로, 이후에 QQ 는 Cholesky Decomposition 을 통해 구할 수 있음.