Duplicate

Lecture 7 | Active Contours

수강 일자
2022/09/27

Deformable Contours

•
a.k.a Active Contours, Snakes
•
initial countour 를 준 뒤, 해당 알고리즘을 반복하게 되면 원하는 boundary 에 fitting 됨.
◦
High gradient 영역 근처에 fitting.
◦
형태가 사각형이면 좋겠다- smooth 하면 좋겠다- 등의 prior 를 반영할 수 있음.
•
Rigid 하지 않고 deformable 한 object (ex. 입술, 손) 에 대해서 shape 을 트래킹할 때 잘 활용됨.
•
바나나 같이 어느정도의 일정한 shape 은 있지만 각각의 물체마다 variety 가 있는 경우에 잘 활용됨.

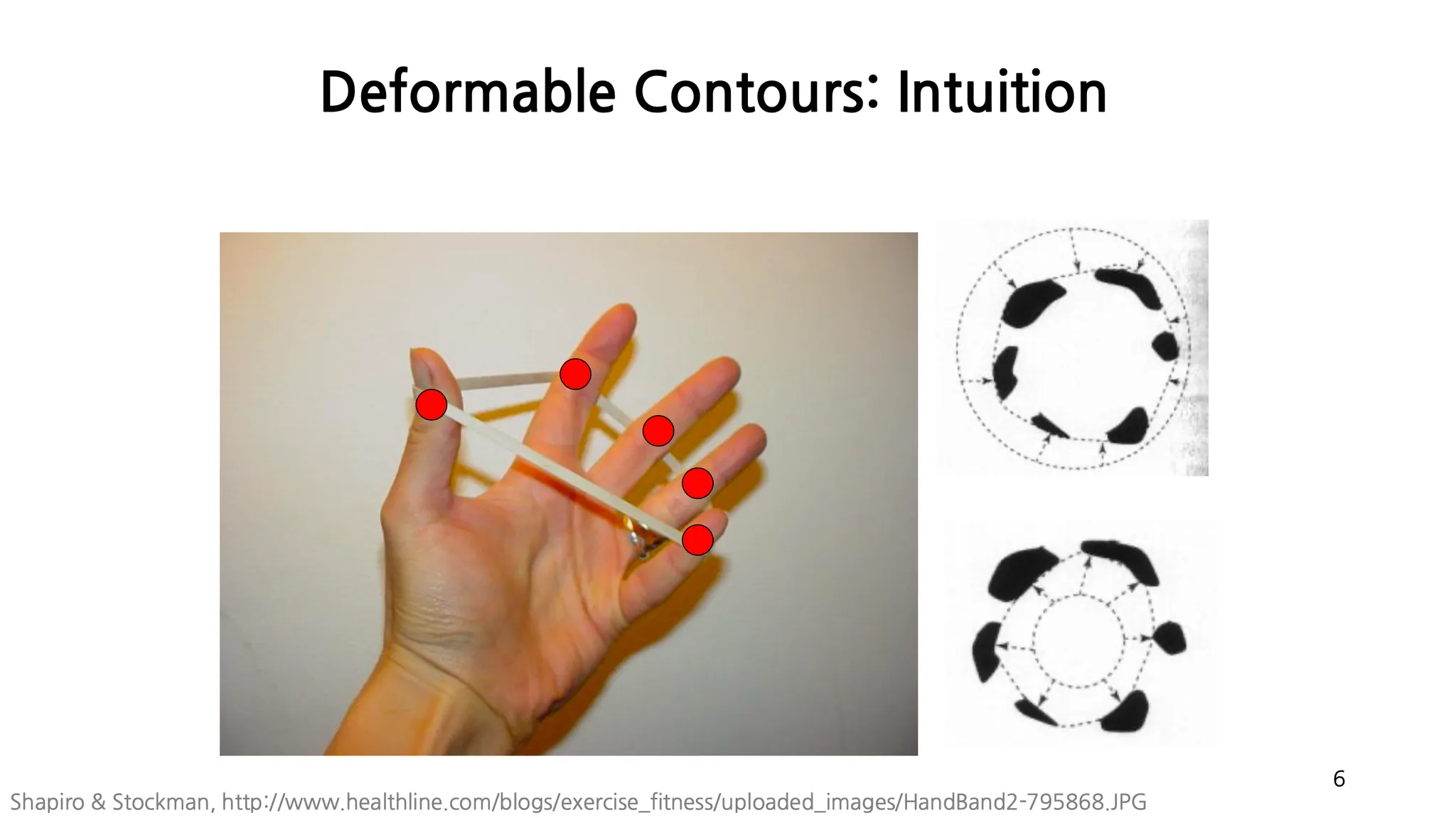
Deformable Contours: Intuition

•
Initial Contour 가 edge 보다 큰 경우 고무밴드처럼 Shape 에 딱 맞도록 축소되어 fitting.
•
Initial Contour 가 edge 보다 작은 경우 고무밴드에서는 그렇지 않지만, edge 에 맞도록 확장되어 fitting.

Snake Energy Function

•
좋은 fitting 이 되었을 때 값이 작아지는 Cost Function 을 설정하면 minimizing problem 으로 변형할 수 있음.
•
Total Energy
Etotal=Einternal+EexternalE_{\rm{total}} = E_{\rm{internal}} + E_{\rm{external}}
◦
Internal energy 는 사전에 존재하는 shape 에 대한 선호도를 반영한 energy 로 선호도를 만족하면 할 수록 작은 값을 가짐. (ex. smoothness, elasticity, particular known shape)
◦
External energy 는 이미지의 구조 (ex. edge) 에 잘 fitting 될 수록 작은 값을 가짐.
◦
좋은 fitting 은 선호도에도 잘 맞고 이미지의 구조를 잘 반영하는 fitting 임.

Parametric Curve Representation

•
연속적인 curve 는 아래와 같이 parameteric 하게 표현할 수 있음.
v(s)=(x(s),y(s)) where 0≤s≤1v(s)=(x(s),y(s)) \ \rm{where}\ 0\le s \le1
◦
선: x(s)=a0+a1sx(s)=a_0+a_1s, y(s)=b0+b1sy(s)=b_0+b_1s 로 지정하면 표현할 수 있음.
◦
원: x(s)=a+rcos⁡sx(s)=a+r\cos s, y(s)=b+rsin⁡sy(s)=b+r\sin s 로 지정하면 표현할 수 있음.

External Energy

•
Edge 위에 curve 가 있을 때 external energy 가 낮아지도록 cost function 을 설정해야 함.
•
Edge 영역에서는 gradient 값이 크므로, contour 를 움직이는 원동력으로 gradient 의 크기에 - 를 붙인 것을 사용해볼 수 있음. 결국 gradient 에 - 를 붙인 cost function 을 설정하면 gradient 가 큰 edge 영역이 해로 나타날 것임.
Eextermal(v(s))=−(∣Gx(v(s))∣2+∣Gy(v(s))∣2)E_{\rm{extermal}}(v(s)) = -(|G_x(v(s))|^2 + |G_y(v(s))|^2)
◦
Gx(x,y)G_x(x,y) 는 I(x,y)I(x,y) 의 xx 방향 gradient 이미지
◦
Gy(x,y)G_y(x,y) 는 I(x,y)I(x,y) 의 yy 방향 gradient 이미지

Internal Energy: Intuition

•
Smooth 한 형태를 원하거나 사전지식을 주려고 할 때 사용할 수 있음.
•
External Energy 만 있다면 edge detection 결과로만 fitting 이 되어 개 앞다리가 울퉁불퉁하게 fitting 되나 사전지식은 그렇게 생기지는 않다- 이기 때문에 보정해줄 수 있음.
•
연속적인 curve 에 대해서는 Bending Energy 를 일반적으로 internal energy 로 사용함.
Einternal(v(s))=α∣dvds∣2+β∣d2vds2∣2E_{\rm{internal}}(v(s))=\alpha|\frac{dv}{ds}|^2 +\beta |\frac{d^2v}{ds^2}|^2
◦
Tension 과 Curvature 가 너무 크지 않도록 함.
◦
Curve 가 parameter ss 에 따라서 너무 심하게 변하는 것은 penalize 함.
◦
Hyperparameter α\alpha, β\beta 는 중요도를 조절할 수 있음. → 첫 번째 Tension term 만 사용하는 경우도 있음.
•
전체 curve 에 대한 internal energy 는 다음과 같음.
Einternal=∫01Einternal(v(s))dsE_{\rm{internal}}=\int_0^1 E_{\rm{internal}}(v(s))ds

Dealing with Missing Data

•
비어 있는 부분들도 Smoothness 때문에 포함되어 fitting 이 됨.

Total Energy

Etotal=Einternal+γEexternalE_{\rm{total}} = E_{\rm{internal}} + \gamma E_{\rm{external}}
•
Eextrenal=∫01Eexternal(v(s))dsE_{\rm{extrenal}} = \int_0^1 E_{\rm{external}}(v(s))ds → Total edge strength under curve
•
Einternal=∫01Einternal(v(s))dsE_{\rm{internal}} = \int_0^1 E_{\rm{internal}}(v(s))ds → Bending Energy

Parameteric Curve Representation

•
때로는 curve 를 연속적이지 않은, discrete 하게 표현하고 싶을 수도 있음.
•
이는 vi=(xi,yi)v_i=(x_i,y_i), i=1,...,ni=1,...,n 인 nn 개의 점으로 표현할 수 있음.
•
External Term
Eexternal=∑i=0n−1∣Gx(vi)∣2+∣Gy(vi)∣2,where vi=(xi,yi)E_{\rm{external}}=\sum_{i=0}^{n-1} |G_x(v_i)|^2 + |G_y(v_i)|^2, {\rm{where}}\ v_i=(x_i,y_i)
•
Internal Term
Einternal=∑i=0n−1α∣vi+1−vi∣2+β∣vi+1−2vi+vi−1∣2,where vi=(xi,yi)E_{\rm{internal}}=\sum_{i=0}^{n-1}\alpha|v_{i+1}-v_i|^2 + \beta|v_{i+1}-2v_i +v_{i-1}|^2, {\rm{where}}\ v_i=(x_i,y_i)
◦
vi=(xi,yi)v_i=(x_i,y_i) 이므로 첫 번째 항목인 Elasticity 만 고려하면 다음과 같이 쓸 수도 있음.
Einternal=α∑i=0n−1(xi+1−xi)2+(yi+1−yi)2E_{\rm{internal}} = \alpha\sum_{i=0}^{n-1}(x_{i+1}-x_i)^2 + (y_{i+1}-y_i)^2
▪
이와 같은 cost function 은 모든 점이 같아질 때 최소가 되어 오류가 발생할 수 있음.
▪
때문에 penalizing term 을 주어 다음과 같이 변경함.
Einternal=α∑i=0n−1∣(xi+1−xi)2+(yi+1−yi)2−dˉ2∣E_{\rm{internal}} = \alpha\sum_{i=0}^{n-1}|(x_{i+1}-x_i)^2 + (y_{i+1}-y_i)^2-\bar{d}^2|
•
dˉ\bar d : 각 점 사이의 거리의 평균 값 (각 iteration 마다 갱신)
•
평균 거리가 어느정도 유지되어야 값이 0 에 가까워짐.
•
α\alpha 에 대한 고찰?
◦
α\alpha 가 크면 internal energy 가 강조 (edge shape 보다는 smoothness, elasticity 가 더 강조된 형태로 fitting)
◦
α\alpha 가 작으면 external energy 가 강조 (smoothness, elasticity 보다는 edge shape 에 더 fitting)

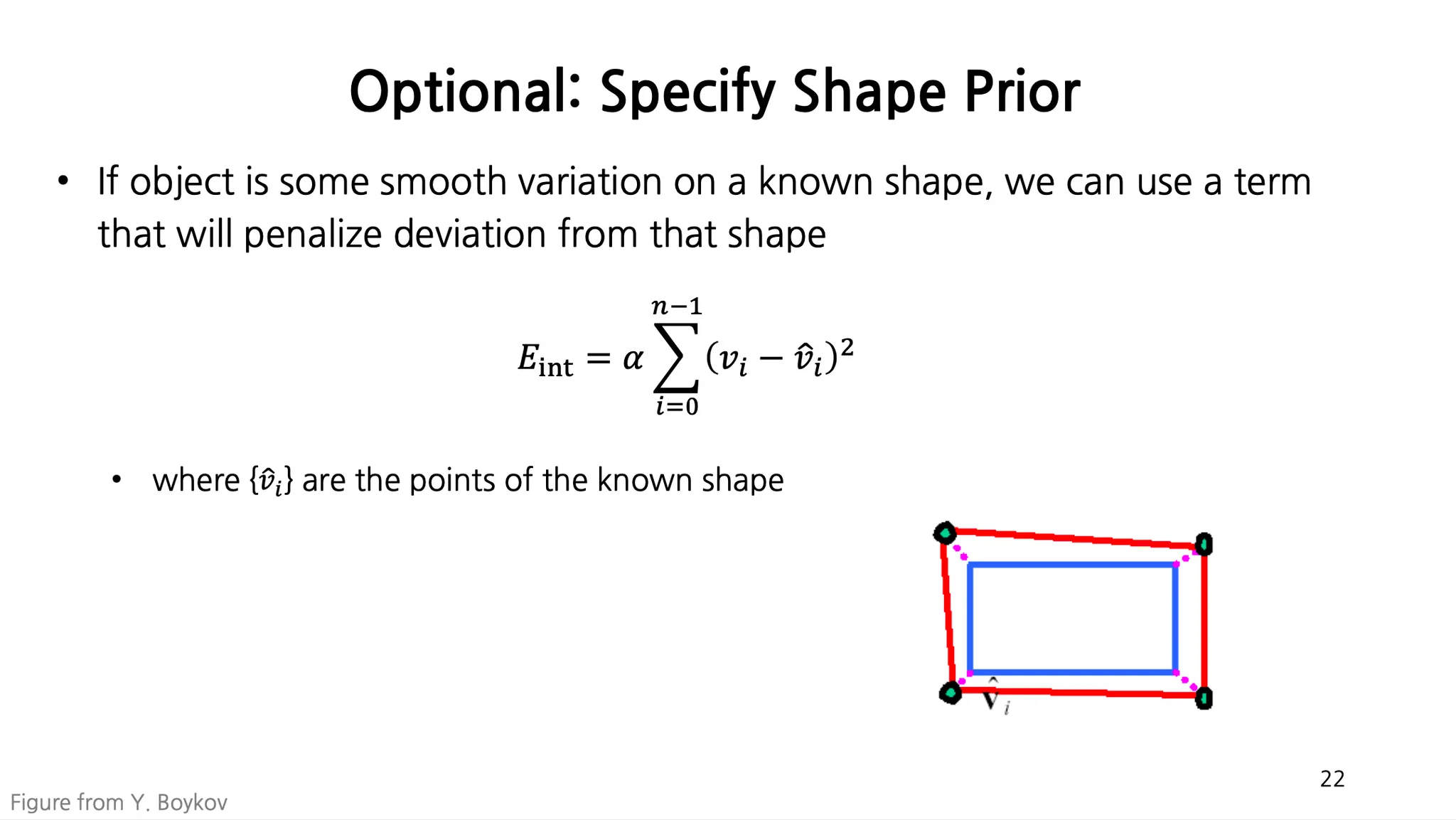
Optional: Specify Shape Prior

•
특정한 형태를 유지하면서 fitting 을 하고 싶을 때 해당 점들의 좌표를 이용해 internal energy 를 정의할 수 있음.
Einternal=α∑i=0n−1(vi−vi^)2E_{\rm{internal}} = \alpha\sum_{i=0}^{n-1} (v_i-\hat{v_i})^2
◦
명시한 점과 멀어질 수록 internal energy 가 커지기 때문에 가깝도록 fitting 이 됨.

Summary: Elastic Snake

•
nn 개의 point 로 정의
•
Internal elastic energy term, external edge-based energy term 이 존재하여 iterative 하게 fitting 됨.
•
물체 근처에서 초기에 정의한 뒤 total energy 를 최소화하는 방향으로 편집함.

Energy Minimization

•
Optimization 은 Computer Vision 영역에서 일반적인 문제이고 다양한 접근으로 해결함.
•
Energy Minimiaztaion: Greedy
1.
각 contour 점들마다 그 점을 중심으로 하는 grid 를 선언함.
2.
격자 내부에 있는 점들 중 energy 가 작은 점들을 선택하여 점을 옮기는 형태로 갱신함.
3.
Stopping Condition 에 도달하면 멈춤.
•
ex. 저번 iteration 혹은 최근 몇 iteration 에서 정한 threshold 이상의 점들이 갱신되지 않았다면 멈춤.
◦
Greedy Algorithm 은 수렴성이 보장되지 않고 좋은 initialization 이 필요함.
•
Energy Minimization: Dynamic Programming
◦
Dynamic Programming 은 optimal solution 을 빠르게 찾아줌.
◦
여러개의 작은 문제로 나누어지고 각각의 작은 문제의 solution 을 구할 수 있으며 원 문제의 solution 을 구하는데 작은 문제의 solution 을 활용할 수 있는 경우에 dynamic programming 을 사용함.
◦
전체 energy 는 pair 점들로 정의할 수 있는 energy 의 sum 형태임.
Etotal(v0,...,vn−1)=∑i=0n−1Ei(vi,vi+1)=−∑i=0n−1∣G(vi)∣2+α∑i=0n−1(vi−vi+1)2E_{\rm{total}}(v_0,...,v_{n-1})=\sum_{i=0}^{n-1}E_i(v_i,v_{i+1}) = -\sum_{i=0}^{n-1}|G(v_i)|^2 + \alpha \sum_{i=0}^{n-1}(v_i - v_{i+1})^2
◦
Ei(vi,vi+1)=∣G(vi)∣2+α(vi−vi+1)2E_i(v_i,v_{i+1})=|G(v_i)|^2 + \alpha(v_i-v_{i+1})^2
◦
Pairwise potential 의 합으로 표현되면 dynamic programming 으로 효과적으로 optimal solution 을 찾을 수 있음!
◦
DP 는 open-ended snake 에 대해서는 잘 동작함.
◦
Closed snake 에 대해서는 v1v_1 에 대해서 고정하고 나머지 open-ended snake 에 대해서 풀고, 고정하는 점들을 바꿔가면서 반복하게 되면 DP 가 수렴하는 solution 을 얻을 수 있음.
◦
위의 open-ended, closed snake 에 대해서는 Message Passing, Belief Propagation 알고리즘과 동일함.
•
Energy Minimization: Gradient Descent
◦
initial point 를 잡고 지속적으로 업데이트하는 방법론.
vi′=vi−t∂E∂viv_i' =v_i-t\frac{\partial E}{\partial v_i}
◦
vi=(xi,yi)v_i=(x_i,y_i) 이므로, ∂E∂vi=[∂E∂xi,∂E∂yi]\frac{\partial E}{\partial v_i} = [\frac{\partial E}{\partial x_i}, \frac{\partial E}{\partial y_i}]
◦
E=−∑i=0n−1∣Gx(xi,yi)∣2+∣Gy(xi,yi)∣2+α∑i=0n−1(xi+1−xi)2+(yi+1−yi)2E = -\sum_{i=0}^{n-1} |G_x(x_i,y_i)|^2 + |G_y(x_i,y_i)|^2 + \alpha\sum_{i=0}^{n-1}(x_{i+1}-x_i)^2 + (y_{i+1}-y_i)^2
◦
Learning rate tt 를 조절하는 것이 어려울 수 있음.
◦
gradient 의 미분을 계산해야 하고 이는 image intensity 에 대해서 이차 미분 항이 포함됨.

Deformable Contours

•
짧은 동영상에 대해서 관심 있는 부분을 트래킹하는데에 많이 사용됨.
1.
첫 번째 frame 에서는 point 를 initialize 한 뒤에 active contour 알고리즘을 이용해 수렴을 시킴.
2.
두 번째 frame 에서는 첫 번째 frame 에서 fitting 된 친구를 initial 로 하여 다시 active contour 알고리즘을 이용해 수렴을 시킴.
3.
이를 반복함.

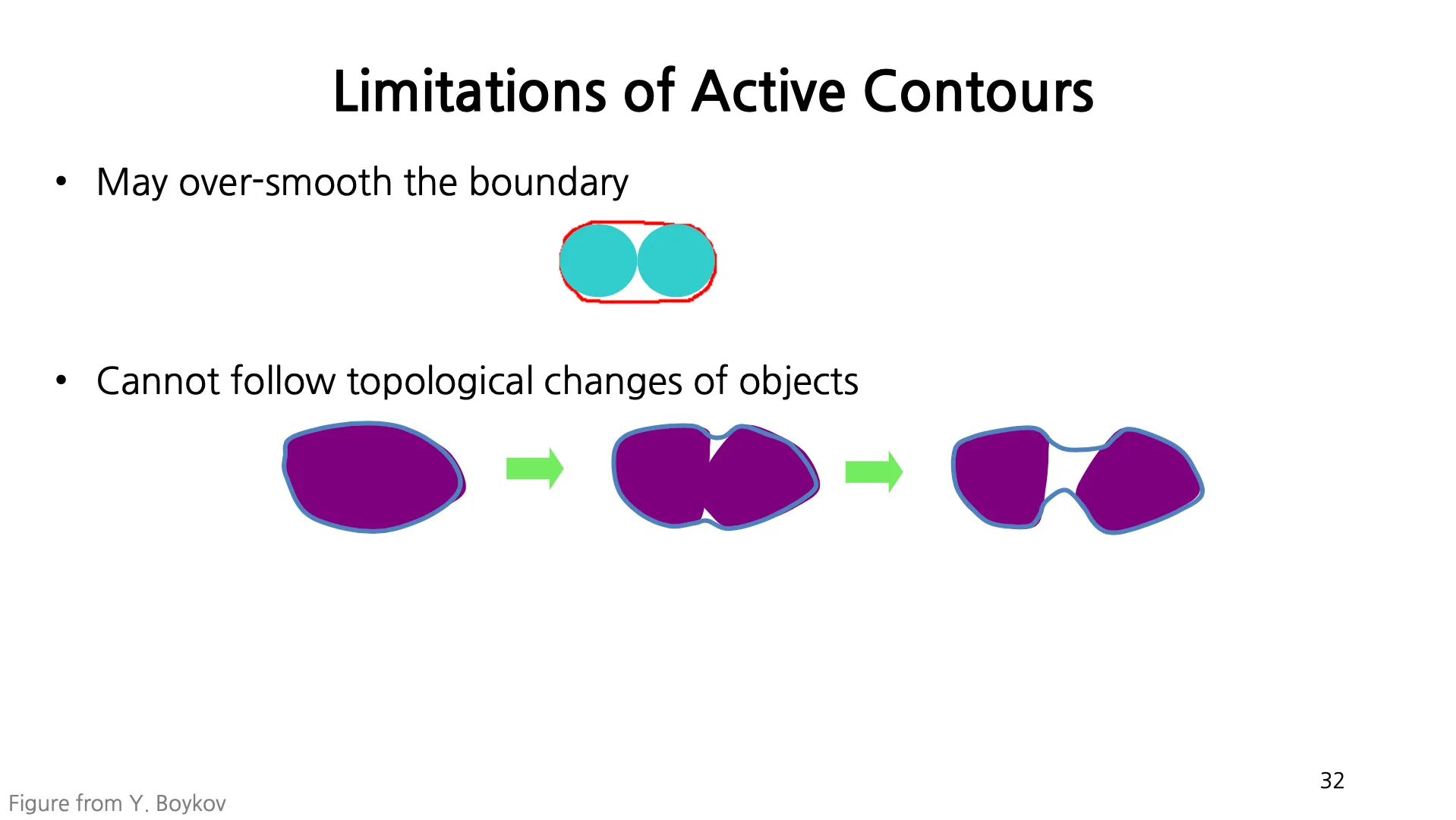
Limitations of Active Contours

•
경우에 따라서 너무 smoothness 가 강하게 주어진 경우에 필요 이상으로 smoothing 이 될 수 있음.
•
구조적인 변화가 생기는 경우에 대한 트래킹이 불가능함. (ex. 세포분열 같이 붙어있다가 떨어진 경우)
•
Edge 가 너무 멀리 떨어져 있는 경우 수렴이 안되는 상황이 생길 수 있음.

Snakes: Pros and Cons

•
Pros
◦
Non-rigid 형태에 대해서 tracking 하거나 fitting 하기에 용이함.
◦
Contour 를 연결된 상태로 유지할 수 있음.
◦
Prior 를 주어서 다양한, 주관적인 contour 를 만들 수 있음.
◦
Energy Function 을 어떻게 정의하고 weighting 을 할 수 있는 flexibility 가 있음.
•
Cons
◦
실제 fitting 하고싶어하는 boundary 에서 너무 멀리 떨어지지 않은 initialization 이 필요함.
◦
Local minima 에 빠져서 원하는 지점까지 수렴하지 않을 수 있음.
◦
Hyperparameter 가 flexibility 를 주기도 하지만 잘 주어야만 원하는 결과를 얻을 수 있고, 이는 쉽지 않은 과정임.

Summary: Main Points

•
Deformable shape (Active Contour) 는 segmentation (boundary 에 fitting)과 tracking (이전의 frame 의 fitting 결과가 다음 frame 의 initial 로 사용)에 효과적임.
•
Cost/Energy optimization 을 하는 일반적인 아이디어를 사용해서 snake 를 opimzation 할 수 있음.
•
Edge 나 Optima 에 있는 지점들이 가진 gradient 가 결과적으로 contour 를 fitting 할 수 있는 attraction force 가 되는 형태의 방법론임. Segmentation 을 위한 input 을 주면 알고리즘이 알아서 fitting 하는 형태.