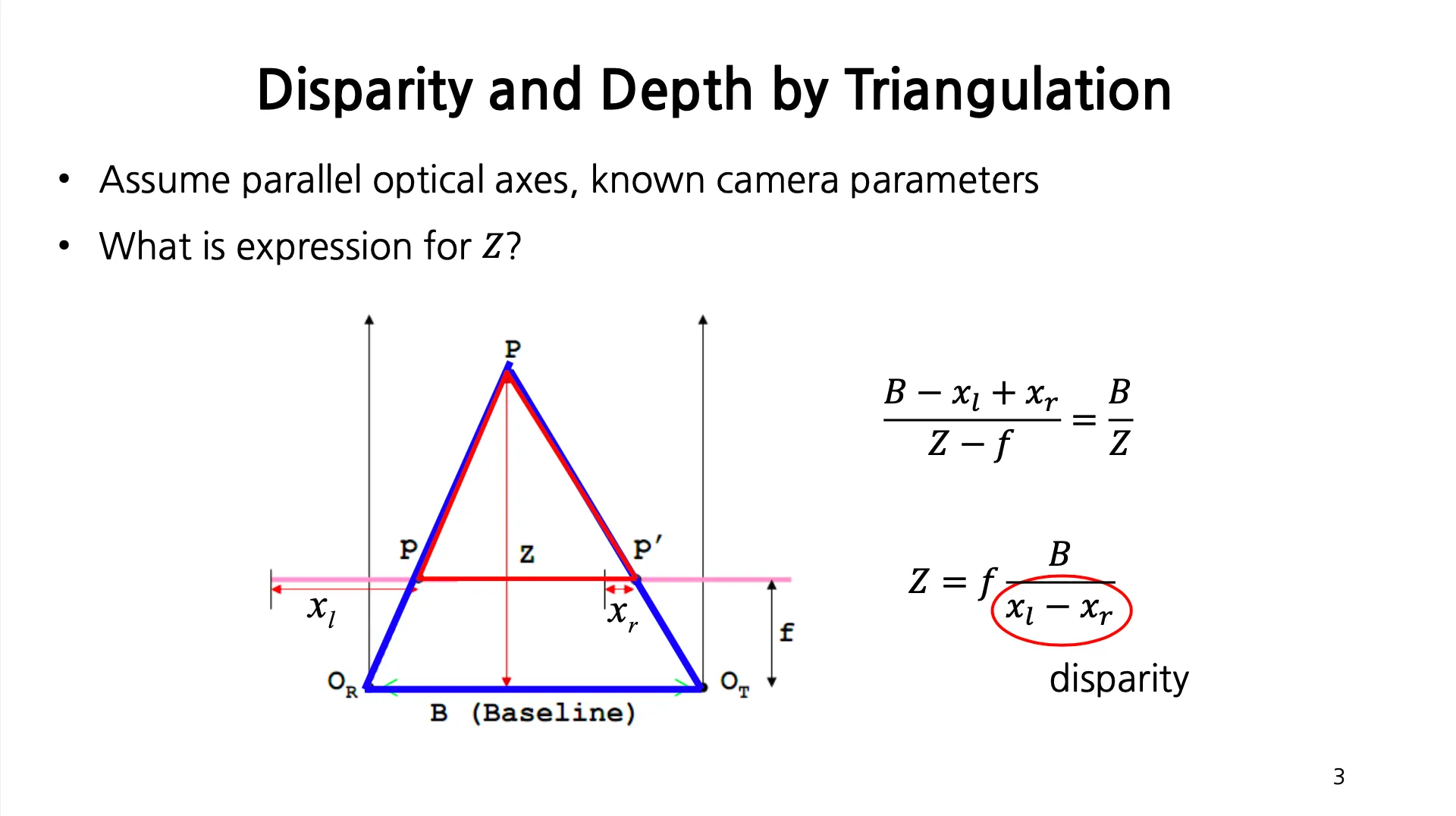
Disparity and Depth (by Triangulation)
•
World Point 의 depth 는 해당 점과 basline 과의 거리
•
Parallel Optical Axes, Known Camera Parameter 조건에서 depth?
◦
: disparity
•
두 이미지에서 corresponding point 의 위치 차이인 disparity 를 나타낸 map 인 Disparity Map 을 활용하고 camera parameter 를 완벽히 안다고 하면, 카메라로부터의 거리 를 구할 수 있음!
The Correspondence Problem
•
Depth Estimation 은 결국 corresponding points 를 찾는 문제가 됨.
•
Epipolar Geometry 는 이러한 corresponding points 를 찾는 문제를 2D → 1D 로 바꾸어줌.
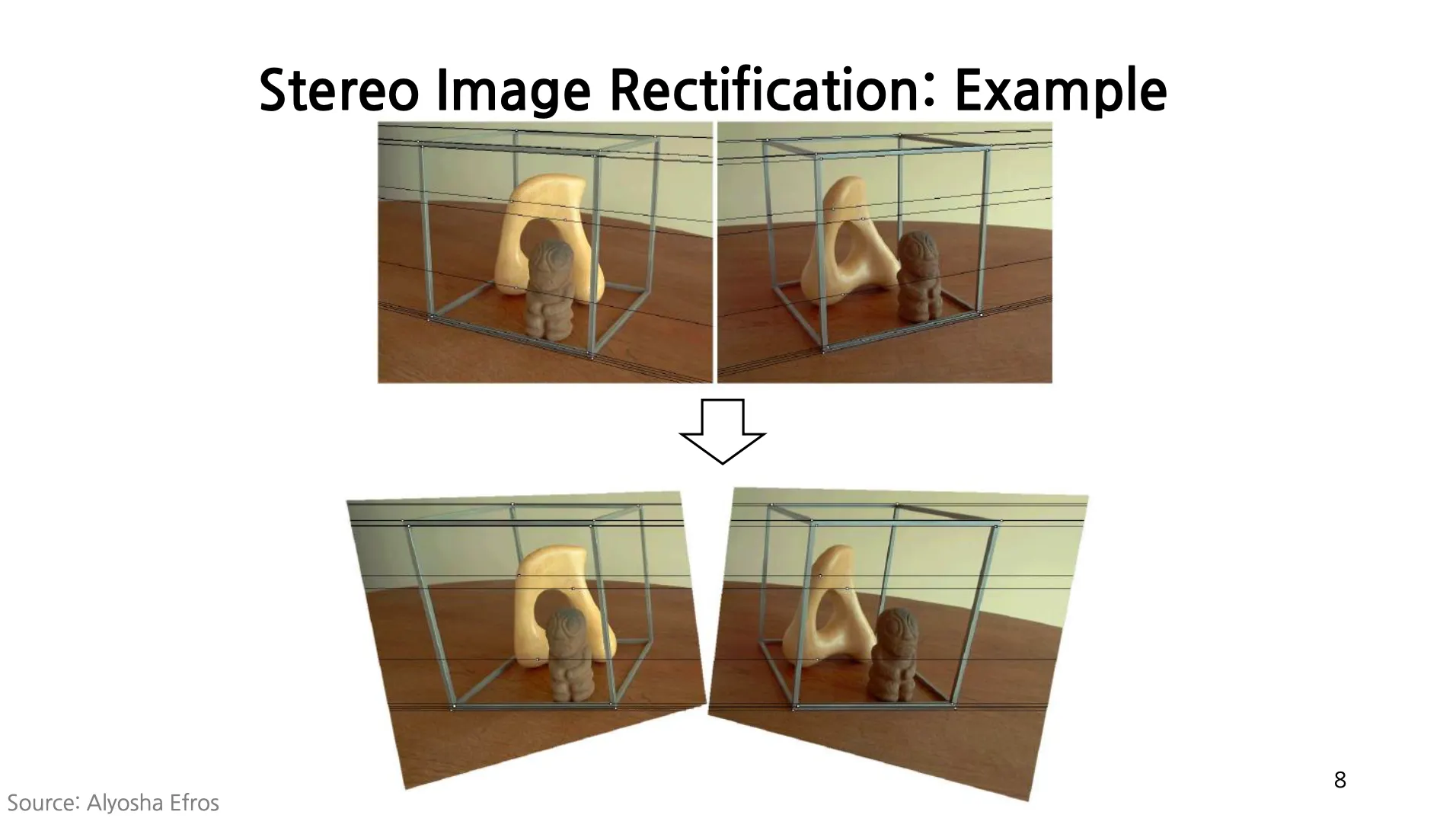
Stereo Image Rectification
•
Image Scanline 을 Epipolar Line 으로 변경하는 것이 편리함.
◦
Epipolar Line 이 동일한 y 값을 가지는 직선이 되도록 homography 를 활용하여 변환
◦
비스듬한 직선 상에서 correspondence 를 찾는 것보다 훨씬 쉬움
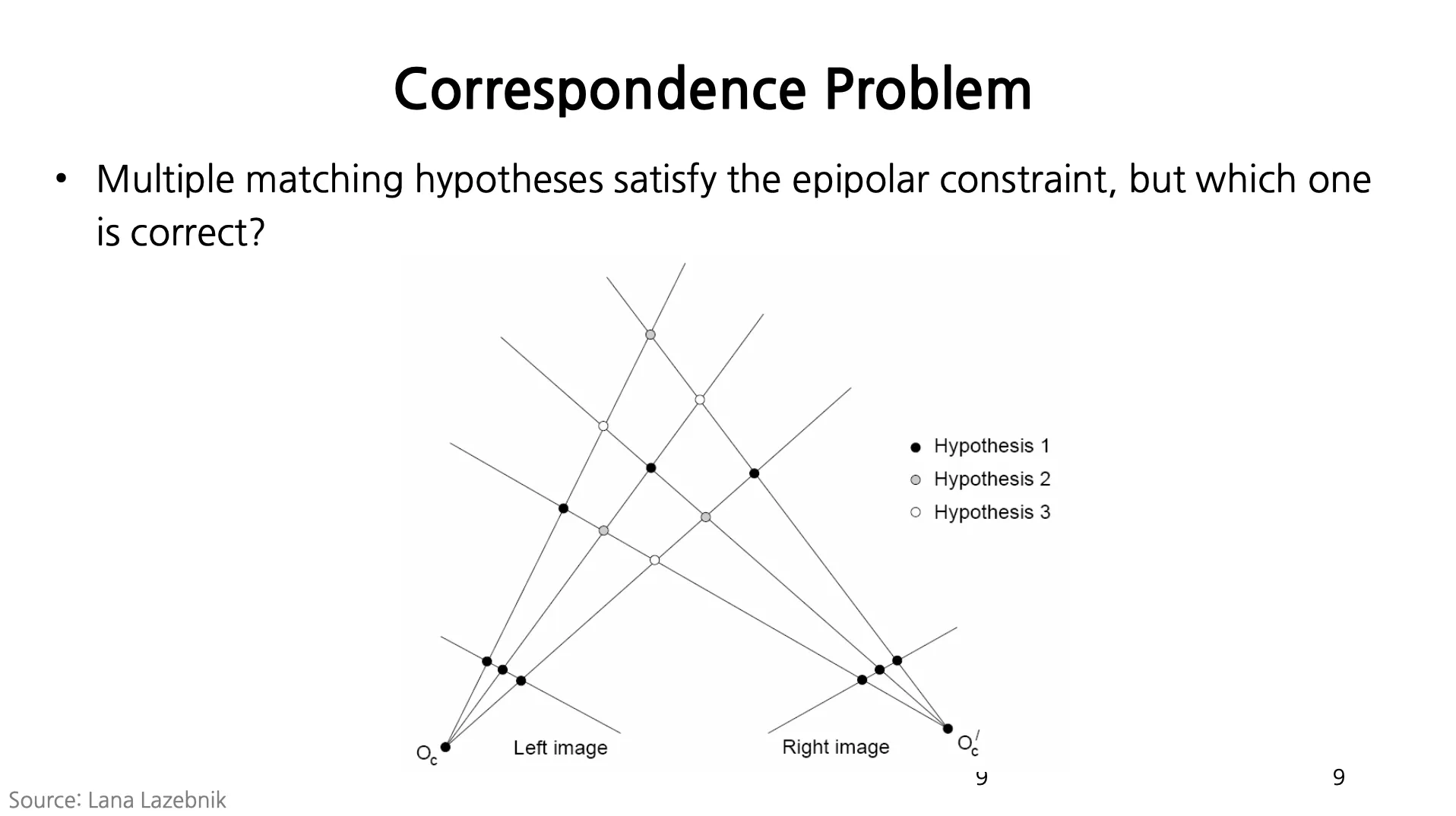
Correspondence Problem
•
Epipolar Geometry 는 2D Search 를 1D Search 로 바꾸어주긴 하지만, 정확한 corresponding point 을 찾아주지는 않음.
◦
Multiple Matching Hypotheses 들 모두가 Epipolar constraint 를 만족하지만, 어느 것이 옳은지는 알 수 없음
Basic Stereo Matching Algorithm
•
Match Windows
1.
Correspondence 를 찾고 싶은 점 주변에 작은 영역(window) 을 정의
2.
정의된 영역을 Epipolar Line 을 따라서 이동시키면서 픽셀값들을 비교
3.
가장 작은 matching cost 를 보이는 영역에 해당되는 점을 corresponding point 로 선언
•
Correspondence Problem 을 간소화하기 위해 Baseline 이 상대적으로 작다는 가정을 넣을 수 있음.
◦
Corresponding point 가 축 상으로 멀지 않은 곳에 있음.
◦
많은 scene point 가 두 view 에서 동시에 볼 수 있음.
◦
Matching region 의 appearance 가 비슷함.
•
Effect of Window Size
◦
Homography 는 Feature Based Corresponding Point 를 찾는 것
◦
Depth Estimation 은 Pixel Based Corresponding Point 를 찾는 것
◦
Window Size 가 작은 경우
▪
얇은 구조체들을 다 detect 하여 얇은 구조체 사이사이의 depth 를 다르게 잘 estimate 함.
▪
작은 영역만을 비교하기 때문에 False Match 가 나올 가능성이 높음.
◦
Window Size 가 큰 경우
▪
얇은 구조체들 사이사이가 뭉개져서 하나의 depth 로 estimate 함.
▪
False Match 가 잘 안나옴.
Limitations of Similarity Constraint
•
Similarity Constraint 의 한계
1.
Background 같은 Textureless Surfaces 경우에는 굉장히 비슷한 영역이 많기 때문에 False Match 가 많이 나옴.
2.
한 쪽 이미지에서는 보이지만, 다른 이미지에서는 보이지 않는 occlusion 이 있을 때는 근원적으로 corresponding point 를 찾을 수 없음.
3.
Non-Lambertian Surface (ex. 금속같은 부분) 의 highlighting 이 다른 위치에서 나타날 수 있고, 다른 부분임에도 matching 이 되버릴 수 있음
How to Improve Window-based Matching?
•
Similarity Constraint 는 local 한 영역의 matching 만을 사용함.
•
Non-local correspondence constraint 도 활용할 필요가 있음.
•
Epipolar Geometry 와 같은 Hard Constraint 외에도, 도움을 줄 수는 있지만 모든 경우에 만족하진 않아도 되는 Soft Constraint 도 있음.
◦
Similarity Constraint
◦
Uniqueness Constraint
▪
한 이미지의 한 점은 다른 이미지의 여러 후보들 중 한 점과만 대응됨.
◦
Disparity Gradient Constraint
▪
Piecewise Continuous Surface 를 가정하고 그 위의 점들의 대응을 찾을 때, 이전 대응점들의 거리를 기반으로 다음 대응 점의 위치로 더욱 타당한 것이 무엇인지 찾을 수 있음.
◦
Ordering Constraint
▪
투명하지 않은 (Opaque) 물체에 대해서는 같은 Surface 위의 점들과 그 대응점들은 동일한 순서로 나열되어 있음.
▪
Transparent Object 와 Occluding Surface 에 대해서는 성립하지 않음.
Better Methods Exist
•
Markov Random Field 라는 apporach 를 사용함
◦
Structured prediction 을 지원하는 framework
◦
Structured prediction 은 어떤 pixel 에 대한 depth 를 예측할 때 그 한 pixel 뿐만 아니라, 주변의 여러 pixel point 에 대한 estimation 을 동시에 하는 방법론
•
Markov Random Field 를 optimization 을 하는 apporach 중 하나가 Graph Cut 임. (자세히 다루지는 않음!)
Vergence
•
두 개의 view 가 어느 정도의 각도를 가지고 바라볼 것인가 를 나타낸 척도
•
Field of view of stereo (두 카메라에 모두 보이는 영역 범위) 는 vergence 가 증가할수록 따라서 증가함.
•
Accuracy 도 vergence 가 증가할수록 따라서 증가함
◦
한 pixel 에 해당되는 영역의 범위가 vergence 가 증가함에 따라서 감소하기 때문임.
◦
Uncertainty of scene point 가 줄어듬.
Role of the Baseline
•
Small Baseline
◦
Large depth error
◦
Easy search problem
•
Large Baseline
◦
Difficult search problem (baseline 이 커지면 뷰에 겹치는 부분이 적기 때문임)
◦
Baseline 이 증가함에 따라서 FOV 가 작고, depth error 가 적고 accuracy 가 증가함/
◦
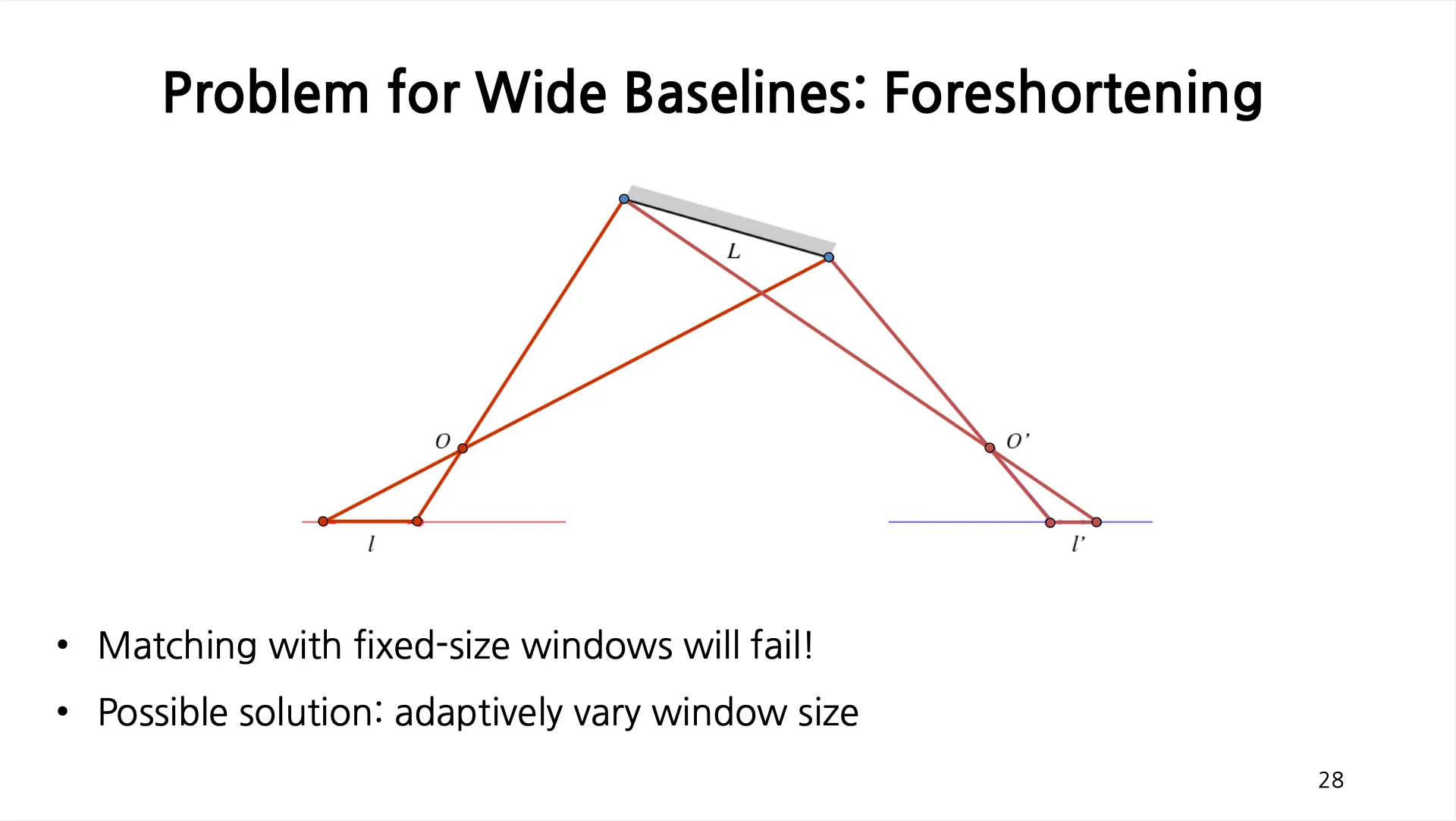
Problem for Wide Baseline: Foreshortening
▪
같은 영역이라도 이미지 상의 길이가 달라짐.
▪
고정된 크기의 windows 는 corresponding point 를 찾기 어려움. → Adaptive 하게 window size 를 변경할 수는 있긴 한데, 대게 많은 경우에 이 과정이 어려움.
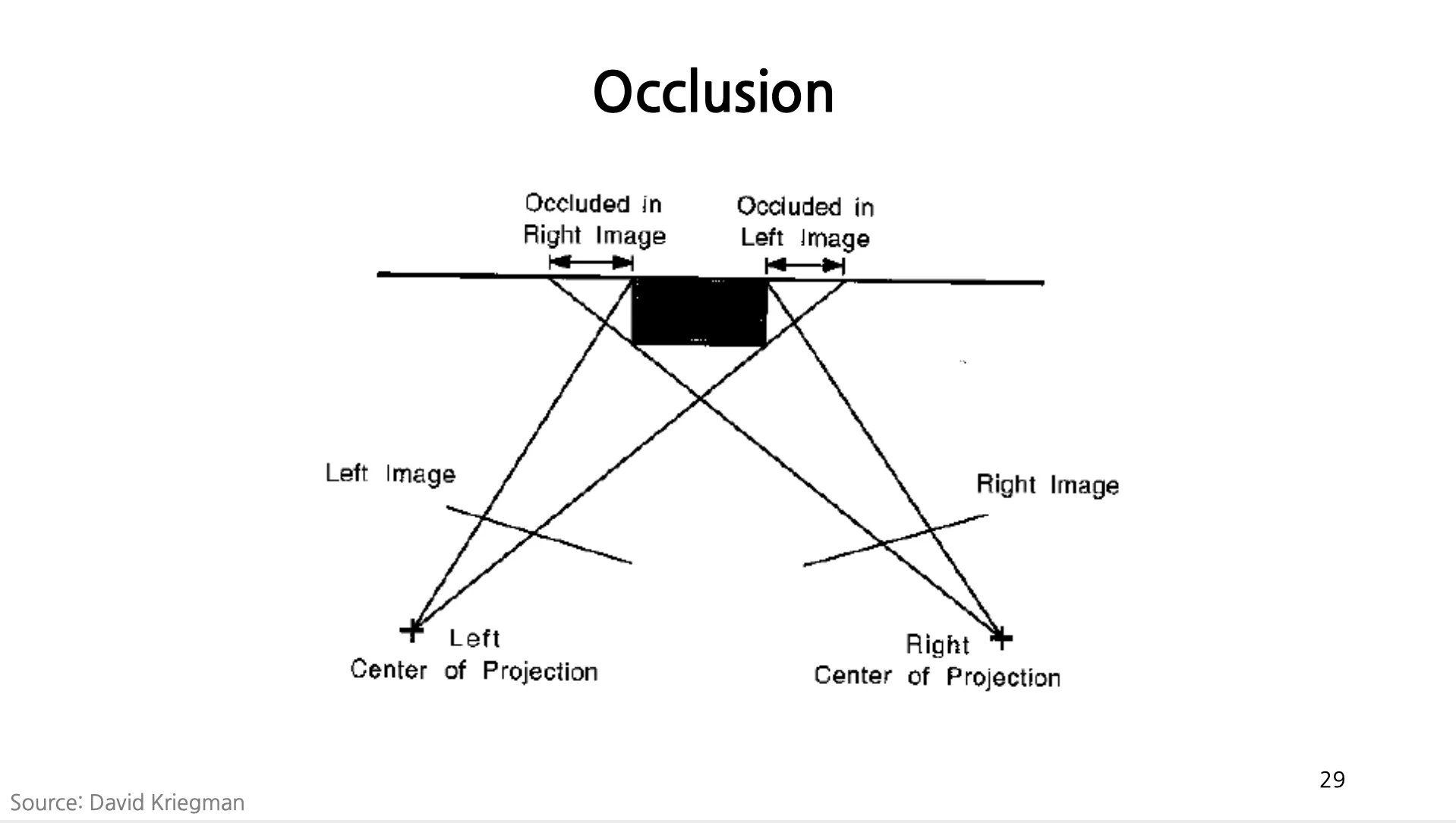
Occlusion
•
가려진 부분에 대해서는 corresponding point 를 찾을 수 없고 depth estimation 이 실패함.
Recap: Stereo with Calibrated Cameras
1.
Baseline 이 아주 크지는 않은 두 이미지가 존재함.
2.
Camera 의 Calibration 을 가정하면 Essential Matrix 를 계산할 수 있음.
•
Canonical camera 가 아닌 경우에는 internal parameter 를 이용한 Fundamental Matrix 를 사용
3.
Epipolar Geometry 를 통해서 rectification 을 함.
4.
Window-based approach + Constraint 들로 Corresponding Point 를 찾음.
5.
구해낸 Corresponding Point 와 Triangulation 으로 depth 를 estimate 할 수 있음.
Error Sources
•
Low-contrast; Textureless 영역에 대한 Corresponding Point 를 찾기 어려움.
•
Occlusion 영역 또한 Corresponding Point 를 찾기 어려움.
•
Essential Matrix 는 External Parameters 를, Fundamental Matrix 는 추가로 Internal Parameters 가 필요한데, 이들에 대한 오차가 있을 수 있음.
•
Corresponding Point 는 동일하게 보여야 하는데 금속과 같은 부분의 Specular Reflection 이 있으면 brightness constancy 가 유지되지 않고 Corresponding Point 를 찾는데 어려움이 있음.
•
Baseline 이 큰 경우 양쪽 이미지에서 보이는 영역이 적고 Corresponding Point 를 찾기 어려움. (Large Motions)
Active Stereo with Structured Light
•
알고 있는 패턴 (”Structured” Light Pattern) 을 물체에 쏘아주고, 그 패턴이 사진기의 상에서 어떻게 보이는지를 바탕으로 3D 형태를 알아내는 방법론
◦
사람 손과 같은 복잡한 3D 구조에서도 Depth Estimation 을 잘 할 수 있음.
•
Laser Scanning (Digital Michelangelo Project)
◦
레이저 슬릿이 카메라에서 어떻게 보이는지를 바탕으로 다비드 상의 3D 구조를 알아냄.
◦
한 번 스캔할 때마다 10초 이상이 걸려 느린 것이 단점이긴 함.
•
Triangulation
◦
Light Pattern 을 쏘는 Laser 가 평면으로 쏘아질 때의 equation 은 다음과 같이 정의함.
◦
Camera 와 그 Image Plane 상의 점 과 대응되는 3차원 지점을 라고 함.
◦
Projection 에 의해 , 는 다음과 같이 표현됨.
◦
가 Light Plane 위에 있어야 하므로 나머지 는 다음과 같음.
Microsoft Kinect
•
알고 있는 패턴의 빛을 쏴줘서 3D 구조를 알아내는 것을 Active Sensing 이라고 함.
•
Commercial 하게 성공했다고 볼 수는 없지만, Computer Vision 영역에 큰 영향을 준 Kinect 가 있음.
◦
Infrared (IR) projector 와 그 패턴을 인지하는 카메라와 일반 RGB 카메라가 있음.
◦
이런 식의 구성의 카메라를 RGB-D 카메라라고 함.
•
IR projector 가 쏴주는 패턴은 눈으로 보았을 때 랜덤한 패턴으로 보이지만, 특허를 받은 패턴이며 해당 패턴으로부터 depth estimation 을 하는 자세한 알고리즘은 미공개임.
RGB-D Datasets
•
3D Vision 은 AR/VR 에 밀접한 관련이 있음.
•
Robotics application 에서도 robot 이 interaction 하려는 주변 환경에 대한 이해가 필요한데, 이를 위해서는 RGB-D 카메라가 필요하기 마련임.
•
RGB-D 카메라로 찍은 데이터셋들이 많음.