Duplicate

Lecture 25 | Classification I - KNN and Naive Bayes

수강 일자
2022/11/28

Classification and Computer Vision

•
컴퓨터비전에서는 수많은, 다양한 종류의 Categorization 을 수행하게 되고, 이는 기계학습의 Classifier 로 구현됨.
◦
ex. Face 인지 아닌지 구분, Handwritten Characters 구분, Scene Classification, Object Recognition
•
Object Detection 을 수행함에 있어서 이미지로부터 작은 patch 를 만들고 patch 영역 내부가 우리가 관심 있는 물체인지 판단하는 Classification 으로 볼 수 있음.

One Simple Method: Skin Detection

•
이미지에서 피부에 해당하는 영역을 구하고 싶은 상황을 가정
•
Skin Classifier 는 특정 pixel 의 R, G, B 값이 피부에 해당하는지 판별하는 Classifier 여야 함.
◦
피부에 대한 학습 데이터와 피부가 아닌 학습 데이터를 직접 labeling 하는 과정이 필요함.

Skin Classification Techniques

•
Nearest Neighbor
◦
가장 가까운 Training Data 를 찾고 해당 Training Data 의 Label 을 예측값으로 산출할 수 있음. (First Nearest Neighbor)
◦
여러 개의 nearest neighbor 를 찾고 voting 하는 형태로 할 수도 있음.
•
Data Modeling
◦
Model the Distribution that generates the data (Generative, 데이터의 분포 자체를 모델링)
◦
Model the boundary (Discriminative, 데이터의 boundary 를 모델링)

Q. What Are Good Feature for…

•
어떤 feature 가 classification 에 좋을까?
◦
Recognizing a beach → Color
◦
Cloth Fabric → Textrue
◦
A mug → Shape
◦
어떤 Classification 을 하느냐에 따라서 중요한 feature 가 달라짐.

What Are the Right Features?

•
Object: Shape (Local Shape Info, Shading, Shadows, Texture …)
•
Scene: Geometric Layout (Linear Perspective, Gradients, Line Segments)
•
Material Properties: Albedo, Feel, Hardness
•
Action: Motion

Image Representations

•
이미지를 벡터공간으로 representation 을 할 때 크게 두 가지 방법이 있음.
◦
Templates (Intensity, Gradients)
◦
Histograms
▪
Feature 들의 distribution 을 나타냄.
▪
Color, Texture, SIFT Descriptors 등

Classifier

•
Feature Space 가 정의역이고 Label 이 공역인 함수
•
많은 경우에는 주어진 학습 데이터를 잘 구분할 수 있는 함수 중에 가장 간단한 것을 선택하는 것이 overfitting 을 예방하는 관점에서 유리함.

Generative vs. Discriminative Classifiers

•
Generative Models
◦
Data 와 Class 사이의 Joint Distribution P(X,Y)P(X,Y) 를 모델링
▪
XX: Feature Space, YY: Label
▪
ex. Naive Bayes, BNs, MRFs, HMM
•
Discriminative Models
◦
Class 들 사이의 Decision Boundary P(Y∣X)P(Y|X) 를 모델링
▪
XX 가 주어졌을 때 YY 를 구하는 것
▪
ex. Logistic Regression, SVMs, Neural Networks, KNN, CRFs
•
Goal: f:X→Yf: X \rarr Y 를 배우는 것
◦
Generative Classifiers
▪
P(X,Y)=P(Y)P(X∣Y)P(X,Y) = P(Y)P(X|Y) 를 구해야 함.
•
Label 이 coarse 가 되고, Data 가 effect 가 됨.
▪
Inference 때는 Bayes Rule 을 사용해 구해낸 P(Y∣X=x)P(Y|X=x) 를 구하게 됨.
◦
Discriminative Classifiers
▪
P(Y∣X)P(Y|X) 를 직접적으로 구함.
▪
Inference 때는 P(Y∣X=x)P(Y|X=x) 를 구하게 됨.
•
Advantages of Generative Models
◦
XX 와 YY 의 상관관계를 모델링할 때 prior 를 적극적으로 활용하기 때문에 적은 데이터셋을 다루거나 Latent Variable, Partially-Labeled Data, Unlabeled Data 를 다루는데 있어서 좋음. (Semi-Supervised, Unsupervised Learning 에서 강점을 가짐.)
◦
데이터 분포 (구조) 의 assumption 을 만들고 사용할 수 있음.
◦
분포로부터 멀리 떨어져 있는 Outlier Detection 을 쉽게 진행할 수 있음.
•
Advantages of Discriminative Models
◦
직접적으로 풀고자하는 문제인 P(Y∣X)P(Y|X) 를 모델링하기 때문에 일반적으로 Classification 성능이 더 좋음.
◦
복잡한 Decision Boundary 도 잘 표현할 수 있음.
•
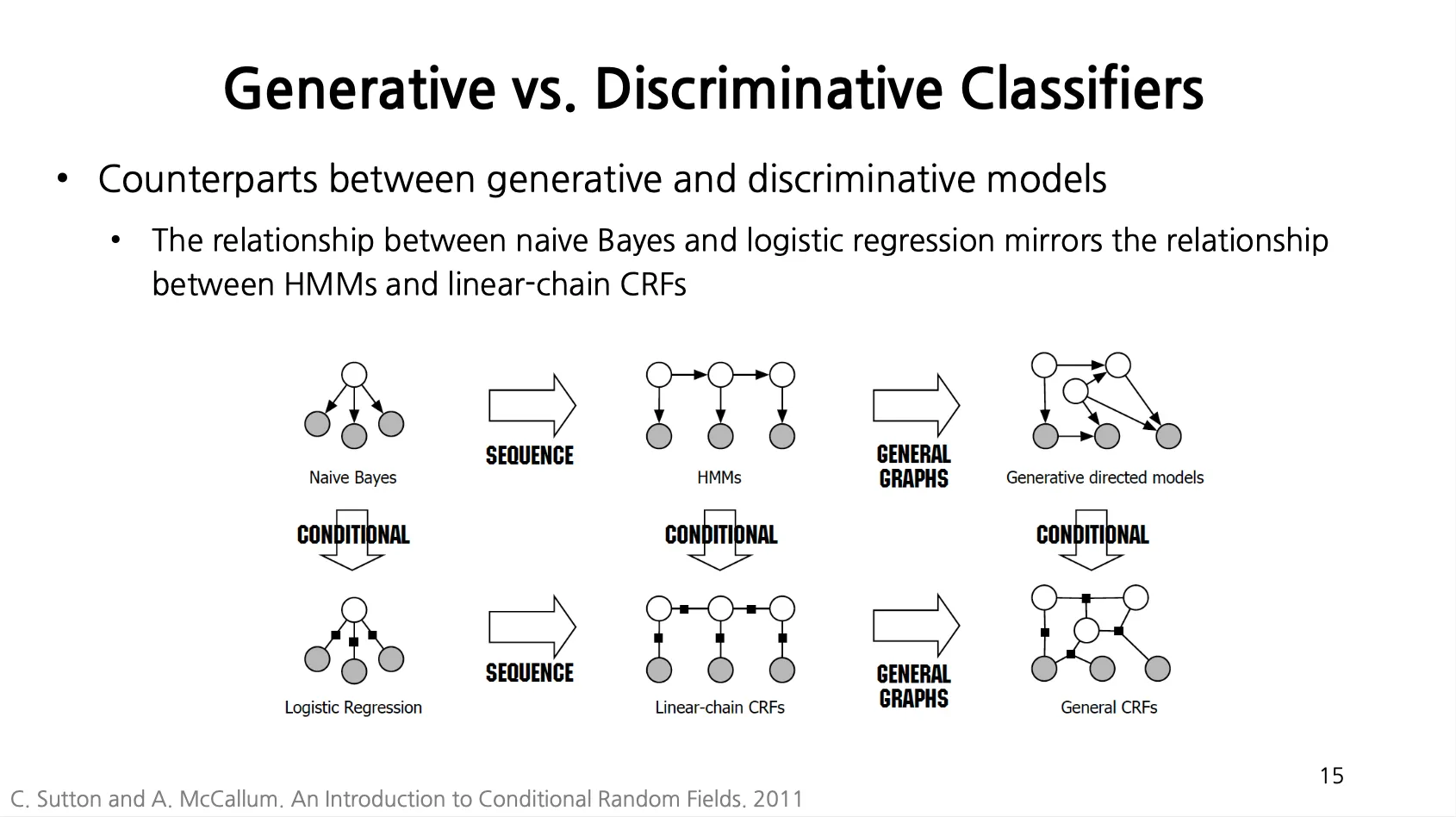
Counterparts between Generative and Discriminative Models
◦
Naive Bayes 와 Logistic Regression 은 동일한 모델인데 각각 Generative, Discriminative Model 임.
◦
Naive Bayes, Logistic Regression 을 각각 sequence 모델로 변형한게 HMMs, Linear-Chain CRFs 임.
◦
HMMs, Linear-Chain CRFs 를 각각 General Graph 모델로 변형한게 Generative Directed Models, General CRFs 임.

Practical Tips

•
Preparing Features for SImple Classifiers
◦
좋은 feature 를 찾기 위해 간단한 Classifiers 를 적용해보는 것이 좋음.
◦
Feature 를 선택하면 Classifier 를 개선하는 과정을 진행하면 됨.
•
Selecting Hyperparameters
◦
ex. Regularization Weights, Cross-Validation
•
Test Multiple Types of Classifiers
•
Imbalanced Classes
◦
현실에서 positive example 을 얻는 경우는 제한되어 있는데 negative example 을 얻는 경우는 쉬움. ex. 암 환자의 X-ray 사진보다 암이 없는 환자의 X-ray 사진이 훨씬 많을 것이고 이에 대한 고려도 필요함.
•
Most Popular Classifiers in Vision
◦
Nearest Neighbor
▪
학습데이터가 많으면 이것만으로도 높은 accuracy 를 얻어낼 수 있음.
◦
Logistic Regression
▪
가장 간단한 Discriminiative Classifier
◦
SVM
▪
DIscriminative Model 중에 가장 많이 쓰이는 Classifier
▪
일반적인 목적으로 Classification 을 하려고 할 때 가장 많이 선택할 만한 Classifier
◦
Ensemble Methos
▪
Classifier 가 주어졌을 때, 여러 개를 써서 서로 도와서 높은 성능을 거둘 수 있게 만드는 접근
▪
ex. Boosted Decision Trees, Random Forest
◦
Deep Networks / CNNs
▪
Representational Learning 을 잘함. (내 목적에 맞는 이미지의 표현 방식을 아주 잘 배울 수 있음.)
▪
기본적으로 복잡하기 때문에 데이터가 많고 계산자원이 많을 때만 동작할 수 있음.

Many Classifiers to Choose from

Exemplar-based Models

•
1-Nearest Neighbor Classifier
◦
Test Example 이 오면 그것과 가장 가까운 Training Example 을 찾고 해당 Label 을 그냥 지정함.
◦
Instance Learning, Memory-based Learning, Lazy Learning 이라고도 부름.
•
K-Nearest Neighbor Classifier
◦
Test Example 이 오면 그것과 가장 가까운 K 개의 nearest neighbor Training Example 을 찾고 해당 Label 중 가장 많은 Label 로 지정함.
◦
Training Data 에 noise 나 outlier 가 있을 때 조금 더 안정적으로 label 을 예측할 수 있음.
◦
Design Choices
▪
Number of Neighbors K
•
Large K: Noise Sensitivity 가 낮음
•
Small K: 공간의 detail, finer 한 구조를 capturing 할 수 있음.
▪
A Distance Metric (거리에 대한 metric)
•
Euclidean Distance 가 가장 대중적임.
•
Cosine Similarity (Angular Similarity) 를 사용하기도 함. (벡터의 방향이 비슷하면 cosine 값이 큼)
cos⁡(θ)=A⋅B∥A∥∥B∥\cos(\theta) = \frac{A \cdot B}{\|A\| \|B\|}
•
Discrete, Biniary 데이터에 대해서는 Hamming Distance 를 구할 수 있음. (다른 dimension 의 개수가 거리가 됨.)
Ham=∑i=1p1(A(i)≠B(i)){\rm Ham} = \sum_{i=1}^p 1(A(i) \ne B(i))
◦
Curse of Dimensionality
▪
예측 정확도가 dimension 이 커지면 커질수록 안좋아짐.
▪
Dimension 이 매우 크면 구별에 몇몇 dimension 은 상관이 없을텐데 이것들도 거리 계산에 사용되게 됨.
▪
Task 에 관련 없는 dimension 은 지우던가, 낮은 차원으로의 mapping 을 하는 것이 중요함.
▪
K 를 증가시키는 것도 하나의 방법이긴 한데, 너무 증가를 시키면 또 효과가 안좋아짐.

Pros and Cons of KNN

◦
Advantages
▪
간단하고, 가장 먼저 테스트해볼만 함. (Feature 가 얼마나 좋은지 테스팅하는데 적합함.)
▪
Tuning 이 적게 필요함.
▪
Training Time 이 필요없음. (Metric Learning 이라고 하여, Distance Function 을 학습을 통해서 배우지 않는 이상)
▪
무한개의 example 을 가지고 있다고 하면, 1-NN 의 error 는 Bayes Optimal Error 의 2배보다 작거나 같음.
•
Bayes Optimal Error 는 도달할 수 있는 가장 작은 Error
◦
Disadvantages
▪
Curse of Dimensionality 를 겪을 수 있음.
▪
Computationally Expensive 할 수 있음.(KD Tree 를 구성하여 NN search 를 빠르게 할 수도 있긴 함.)
▪
Outlier 에 sensitve 함. 피하기 위해서는 K 를 큰 값으로 줄 수 있음.

Generative Classifiers

•
Feature 와 Label 사이의 Joint Distribution 을 모델링하여 분류하는 Classifier
◦
Prior 를 포함할 수 있음.
◦
Semi-Supervised / Unsupervised Learning 을 핸들링할 수 있음.
◦
ex. Naive Bayes, Mixture of Gaussians for each calss
•
Using Naive Bayes
◦
Generative Classifier 중에 가장 기초가 되는 Classifier
◦
Train / Test 가 빠름

Bayes Classifier

•
Goal: 주어진 features x1,x2,…,xnx_1, x_2, \dots, x_n 을 사용해 label yy 를 예측하는 것
•
다음과 같은 Digit Recognition 의 상황을 가정
◦
x1,x2,…,xn∈{0,1}x_1, x_2, \dots, x_n \in \{ 0,1\}
◦
y∈{5,6}y \in \{5,6 \}
•
다음의 방법론으로 XX에 적합한 yy 에 대한 예측을 할 수 있음.
arg max⁡yP(y∣x1,…,xn)\argmax_y P(y |x_1,\dots,x_n)
•
이를 Bayes Rule 을 이용해 다음과 같이 변형할 수 있음.
P(y∣x1,…,xn)=P(x1,…,xn∣y)P(y)P(x1,…,xn)P(y |x_1,\dots,x_n) = \frac{P(x_1,\dots, x_n|y)P(y)}{P(x_1,\dots, x_n)}
◦
Posterior 는 xx 가 주어졌을 때 yy 를 알아내는 것, Likelihood 는 yy 가 주어졌을 때 xx 를 알아내는 것
◦
분자의 첫 항은 Likelihood, 분자의 두 번째 항은 Prior
◦
분모 항은 Normalization Constant

Naive Bayes Classifier

P(y=5∣x1,…,xn)=P(x1,…,xn∣y=5)P(y=5)P(x1,…,xn∣y=5)P(y=5)+P(x1,…,xn∣y=6)P(y=6)P(y=5|x_1,\dots,x_n) = \frac{P(x_1,\dots,x_n| y=5)P(y=5)}{ P(x_1,\dots,x_n| y=5)P(y=5) + P(x_1,\dots,x_n| y=6)P(y=6)}
P(y=6∣x1,…,xn)=P(x1,…,xn∣y=6)P(y=6)P(x1,…,xn∣y=5)P(y=5)+P(x1,…,xn∣y=6)P(y=6)P(y=6|x_1,\dots,x_n) = \frac{P(x_1,\dots,x_n| y=6)P(y=6)}{ P(x_1,\dots,x_n| y=5)P(y=5) + P(x_1,\dots,x_n| y=6)P(y=6)}
•
분모 항은 Marginalization 을 활용해 변형함.
◦
모든 조건부에 대한 합으로 무조건부 확률을 구해냄.
•
분자의 네 개의 항목을 알면 다 구할 수 있음. → 이를 학습과정을 통해서 얻어냄.
•
Naive Bayes Assumption 을 가져옴.
◦
Naive Bayes Assumption: yy 가 주어지면 xix_i 들 끼리는 독립이다 (Conditional Independence)
P(x1,…,xn∣y)=∏i=1nP(xi∣y)P(x_1,\dots,x_n|y) = \prod_{i=1}^n P(x_i|y)
◦
이러한 assumption 을 적용하면 학습해야 할 parameters 수가 줄어듬.
▪
기존에는 P(x1,…,xn∣y)P(x_1,\dots,x_n|y) 를 학습하기 위해 2n−12^n -1 개의 paramter 가 필요했음.
▪
적용 후에는 P(x1∣y),⋯ ,P(xn∣y)P(x_1|y), \cdots, P(x_n|y) 만 구하면 되서 nn 개의 paramter 가 필요함.

Naive Bayes Training

1.
First, Collect Data
2.
Training in Naive Bayes (easy!)
•
Maximum Likelihood Esimtation (MLE) 을 활용함.
•
P(y=v)P(y=v) 를 데이터셋에서의 records fraction 으로 예측함.
P(y=v)=count(y=v)# dataP(y=v)=\frac{{\rm{count}}(y=v)}{{\rm \#\ data}}
◦
5 와 6 데이터가 동일한 개수면 0.5 씩을 가져감.
•
P(xi=u∣y=v)P(x_i=u|y=v) 를 데이터셋에서의 records fraction 으로 마찬가지로 예측함.
P(xi=u∣y=v)=count(xi=u∧y=v)count(y=v)P(x_i=u|y=v)=\frac{{\rm{count}}(x_i=u \land y=v)}{{\rm count}(y=v)}
◦
하지만, 몇몇 counts 가 0이 될 수도 있는데 (P(x1,…,xn∣y)P(x_1,\dots,x_n|y) 를 구할 때 0 을 곱하면 0 이 되어버리므로)Training Data 가 적어서 생긴 이슈일 수도 있어서 smoothing 차원에서 virtual counts 를 넣어주기도 함.
P(xi=u∣y=v)=count(xi=u∧y=v)+1count(y=v)+2P(x_i=u|y=v)=\frac{{\rm{count}}(x_i=u \land y=v)+1}{{\rm count}(y=v)+2}
•
이와 같은 paramter estimation 을 MAP estimation 이라고 함.

Summary of Naive Bayes

•
가장 간단한 Bayes Classifier 중 하나
◦
P(x1,…,xn∣y)P(x_1,\dots, x_n|y) 를 구하는 것이 intractable 함. (복잡도가 지수형태이므로)
◦
Naive Bayes Assumption 을 가정하여 위를 해결함. (yy 가 주어지면 xix_i 끼리는 conditionally independent 하다는 가정) → 사실 맞는 경우는 별로 없는데 이 가정을 넣어도 잘 동작함.
•
Remarks
◦
구현이 쉽고 잘 동작함.
◦
처음 시도하기에 굉장히 좋음.
◦
Logistic Regression 이 Discriminative Alterative 임.