Duplicate

Lecture 3 | Frequency Domain Analysis

수강 일자
2022/09/13

Why Fourier Transform

•
Image Processing 은 2D Signal 의 Filtration 임.
•
Spatial Domain 에서의 Filtration 은 Convolution 을 사용하는 것과 다르게, Frequency Domain 에서의 Filtration 은 Fourier Transfrom 이후 Multiplication 을 사용.
•
Input Image 를 Frequency Domain 으로 변경하여 Frequency Filter 인 Fourier Transform 을 적용하고 다시 Spatial Domain 으로 변경하는 과정을 진행할 수도 있음.

Basics of Sine/Cosine

•
Asin⁡(wx+φ),Bcos⁡(wx+φ)A\sin(wx+\varphi), B\cos(wx+\varphi)
•
ω\omega: angular frequency 로, 2π2\pi 안에 얼마나 oscillation 이 존재하는지를 나타냄.
•
ff: common frequency 로, unit time 안에 얼마나 oscillation 이 존재하는지를 나타냄.
•
f=1T=ω2πf=\frac{1}{T}=\frac{\omega}{2\pi}
•
phase 는 cosine function 을 xx 축 기준으로 얼마나 shifting 해서 얻어냈는지를 의미함.
◦
sin⁡(ωx)→cos⁡(ωx−π2)\sin(\omega x) \rarr \cos(\omega x-\frac{\pi}{2}) 이므로 π2\frac{\pi}{2} 의 phase 를 가짐

How to Represent Signals?

•
Option 1: Taylor Series
f(x)=f(a)+f′(a)(x−a)+f′′(a)2!(x−a)2+f(3)(a)3!(x−a)3+...+f(n)(a)n!(x−a)n+...f(x)=f(a) + f'(a)(x-a)+\frac{f''(a)}{2!}(x-a)^2 + \frac{f^{(3)}(a)}{3!}(x-a)^3+...+\frac{f^{(n)}(a)}{n!}(x-a)^n+...
◦
주어진 signal 을 다항식으로 표현
◦
Frequency 기반으로 표현이 가능하기 때문에 얼마나 빠르게, 자주 signal 이 바뀌는지를 이야기하기 편함.
◦
Polynomial 은 치역이 −∞-\infty 와 ∞\infty 의 범위 안에서 정의되기 때문에 어떤 signal 이 특정 영역에만 존재한다면 polynomial 을 더해서 나머지 범위를 cancel 시켜주어야 하기 때문에 unstable 함.
◦
3차항, 4차항이 어떻게 되었는지가 물리적으로 의미하는 바가 따로 없음. (Physically Unmeaningful)
•
Option 2: Fourier Series
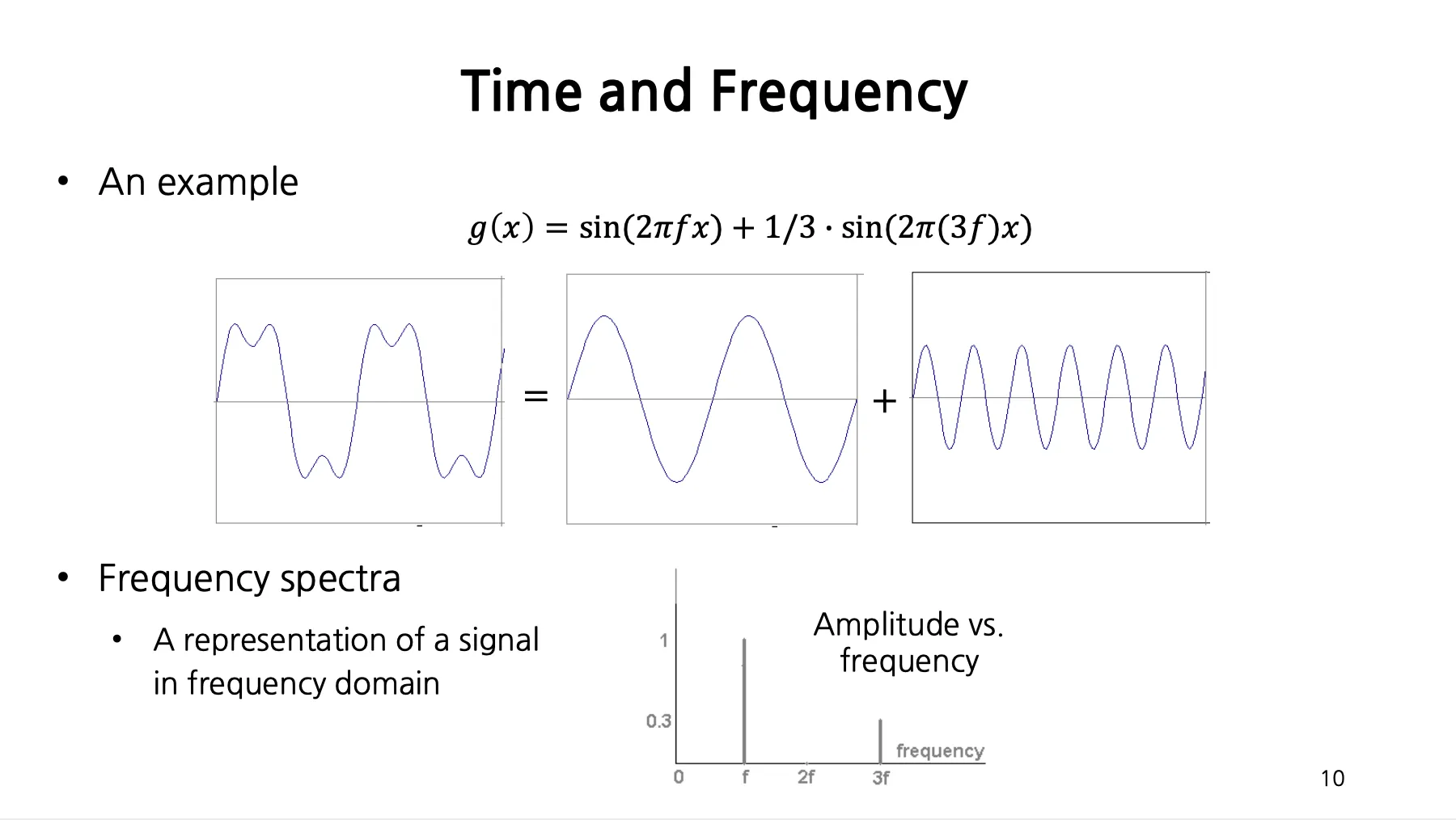
f(x)=A02+∑n=1NAncos⁡(2πLnx−φn)f(x)= \frac{A_0}{2} + \sum_{n=1}^N A_n \cos(\frac{2\pi}{L}nx - \varphi_n)
◦
모든 주기함수는 sine/cosine 의 합으로 표현할 수 있음.
◦
주기가 LL 인 주어진 signal 을 Magnitude 와 Phase 를 coefficient 로 가지는 주기가 12\frac{1}{2} 배씩 감소하는 sinusoidal 의 합으로 나타냄.
◦
Magnitude 와 Phase 를 복소수를 사용해 Magnitude 를 복소평면에서 원점과 좌표 사이의 거리로, Phase 를 복소평면에서 실수축과 이루는 각도로 생각해서 정의할 수 있음.
◦
Frequency Spectra
▪
어떤 Amplitude (Magnitude) 와 Frequency 를 가지는 component 로 구성되어 있는지를 나타내주는 도표

Fourier Transform

F(ω)=∫−∞∞f(x)exp⁡(−iωx)dx=∫−∞∞f(x)cos⁡ωxdx−i∫−∞∞f(x)sin⁡ωxdx\begin{align*} F(\omega)&=\int_{-\infty}^\infty f(x)\exp(-i\omega x)dx \\ &= \int_{-\infty}^\infty f(x)\cos \omega x dx - i\int_{-\infty}^\infty f(x)\sin \omega x dx \end{align*}
◦
Time/Spatial Domain 의 representation 인 f(x)f(x) 를 Frequency Domain 의 representation 인 F(ω)F(\omega) 로 변경하는 과정.
◦
Periodic Signal 에 적합한 변환 과정이며, 그렇지 않은 경우에는 Windowed Fourier Transform, Wavelet, Gabor Filter 등을 사용해야 함.
◦
F(ω):R→CF(\omega): \mathbb{R}\rarr \mathbb{C}
◦
Inverse Fourier Transform (IFT)
f(x)=12π∫−∞∞F(ω)exp⁡(iωx)dωf(x)=\frac{1}{2\pi}\int_{-\infty}^\infty F(\omega)\exp(i\omega x)d\omega
▪
Dirac-Delta Impulse 의 FT 와 Constant Function 1 의 IFT
f(x)=δ(x)→F(ω)=∫−∞∞δ(x)exp⁡(−iωx)dx=1F(ω)=1→f(x)=12π∫−∞∞1⋅exp⁡(iωx)dω=δ(x)f(x)=\delta(x) \rarr F(\omega)=\int_{-\infty}^\infty \delta(x)\exp(-i \omega x )dx=1\\ F(\omega)=1 \rarr f(x)=\frac{1}{2\pi}\int_{-\infty}^\infty 1\cdot\exp(i \omega x )d\omega=\delta(x)\\

Fourier Transform Pairs

•
Fourier Transform of Cosine Function
f(x)=cos⁡(ω0x)=12(exp⁡(iω0x)+exp⁡(−iω0x))→F(ω)=∫−∞∞12(exp⁡(iω0x)+exp⁡(−iω0x))exp⁡(−iωx)dx=12∫−∞∞(exp⁡(−i(ω−ω0)x)+exp⁡(−i(ω+ω0)x))dx=πδ(ω−ω0)+πδ(ω+ω0)f(x) = \cos(\omega_0x)=\frac{1}{2}(\exp(i\omega_0 x) + \exp(-i\omega_0 x)) \rarr \\ \begin{align*} F(\omega) &= \int_{-\infty}^\infty \frac{1}{2}(\exp(i\omega_0 x) + \exp(-i\omega_0 x))\exp(-i\omega x) dx \\ &= \frac{1}{2}\int_{-\infty}^\infty (\exp(-i(\omega-\omega_0) x) + \exp(-i(\omega+\omega_0) x))dx \\ &= \pi\delta(\omega-\omega_0) + \pi\delta(\omega+\omega_0) \end{align*}
•
Fourier Transform of Sine Function
f(x)=sin⁡(ω0x)=12i(exp⁡(iω0x)−exp⁡(−iω0x))→F(ω)=∫−∞∞12i(exp⁡(iω0x)−exp⁡(−iω0x))exp⁡(−iωx)dx=12i∫−∞∞(exp⁡(−i(ω−ω0)x)−exp⁡(−i(ω+ω0)x))dx=−iπδ(ω−ω0)+iπδ(ω+ω0)f(x)=\sin(\omega_0 x) = \frac{1}{2i}(\exp(i\omega_0 x )-\exp(-i\omega_0 x) ) \rarr \begin{align*} F(\omega) &= \int_{-\infty}^\infty \frac{1}{2i}(\exp(i\omega_0 x) - \exp(-i\omega_0 x))\exp(-i\omega x) dx \\ &= \frac{1}{2i}\int_{-\infty}^\infty (\exp(-i(\omega-\omega_0) x) - \exp(-i(\omega+\omega_0) x))dx \\ &= -i\pi\delta(\omega-\omega_0) + i \pi\delta(\omega+\omega_0) \end{align*}
•
Fourier Transform of Gaussian Function
f(x)=12πσexp⁡(−x22σ2)→F(ω)=exp⁡(−σ2ω22)f(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{x^2}{2\sigma^2}) \rarr F(\omega)=\exp(-\frac{\sigma^2\omega^2}{2})
◦
Gaussian 을 FT 하면 Gaussian 과 유사한 형태가 나옴.

Properties of Fourier Transform

f(x)→F(ω)g(x)→G(ω)f(x) \rarr F(\omega) \\ g(x) \rarr G(\omega)
•
Linearity
c1f(x)+c2g(x)→c1F(ω)+c2G(ω)c_1f(x)+c_2g(x) \rarr c_1F(\omega) + c_2G(\omega)
•
Scaling
f(ax)→1∣a∣F(ωa)f(ax) \rarr \frac{1}{|a|}F(\frac{\omega}{a})
•
Shifting
f(x−T)→exp⁡(−iωT)F(ω)f(x-T) \rarr \exp(-i\omega T)F(\omega)
•
Symmetry
F(x)→f(−ω)F(x) \rarr f(-\omega)
•
Conjugation
f∗(x)→F∗(−ω)f^*(x) \rarr F^*(-\omega)
•
Convolution
f(x)∗g(x)→F(ω)G(ω)f(x)*g(x) \rarr F(\omega)G(\omega)
•
Differentiation
dnf(x)dxn→(iω)nF(ω)\frac{d^nf(x)}{dx^n} \rarr (i\omega)^nF(\omega)

Fourier Transform and Convolution

•
g(x)=f(x)∗h(x)g(x) = f(x) * h(x) 일 때 G(ω)G(\omega) 을 구해보자!
G(ω)=∫−∞∞g(x)exp⁡(−iωx)dx=∫−∞∞∫−∞∞f(τ)h(x−τ)dτexp⁡(−iωx)dx=∫−∞∞f(τ)∫−∞∞h(x−τ)exp⁡(−iωx)dxdτ=∫−∞∞f(τ)∫−∞∞h(v)exp⁡(−iω(v+τ))dvdτ=∫−∞∞f(τ)exp⁡(−iωτ)dτ∫−∞∞h(v)exp⁡(−iωv)dv=F(ω)H(ω)\begin{align*} G(\omega) &= \int_{-\infty}^\infty g(x)\exp(-i\omega x)dx \\ &= \int_{-\infty}^\infty \int_{-\infty}^\infty f(\tau)h(x-\tau)d\tau \exp(-i\omega x)dx \\ &= \int_{-\infty}^\infty f(\tau) \int_{-\infty}^\infty h(x-\tau) \exp(-i\omega x)dxd\tau\\ &= \int_{-\infty}^\infty f(\tau) \int_{-\infty}^\infty h(v) \exp(-i\omega (v+\tau))dvd\tau\\ &= \int_{-\infty}^\infty f(\tau)\exp(-i \omega\tau)d\tau \int_{-\infty}^\infty h(v) \exp(-i\omega v)dv\\ &= F(\omega)H(\omega) \end{align*}
•
Spatial Domain 에서의 convolution 은 Frequency Domain 에서의 곱셈과 같음!
•
즉 Spatial Domain 에서의 convolution 을 구하기 위해서 두 함수를 Fourier Transform 하여 곱셈을 한 뒤 나온 값을 IFT 를 거칠 수 있음.

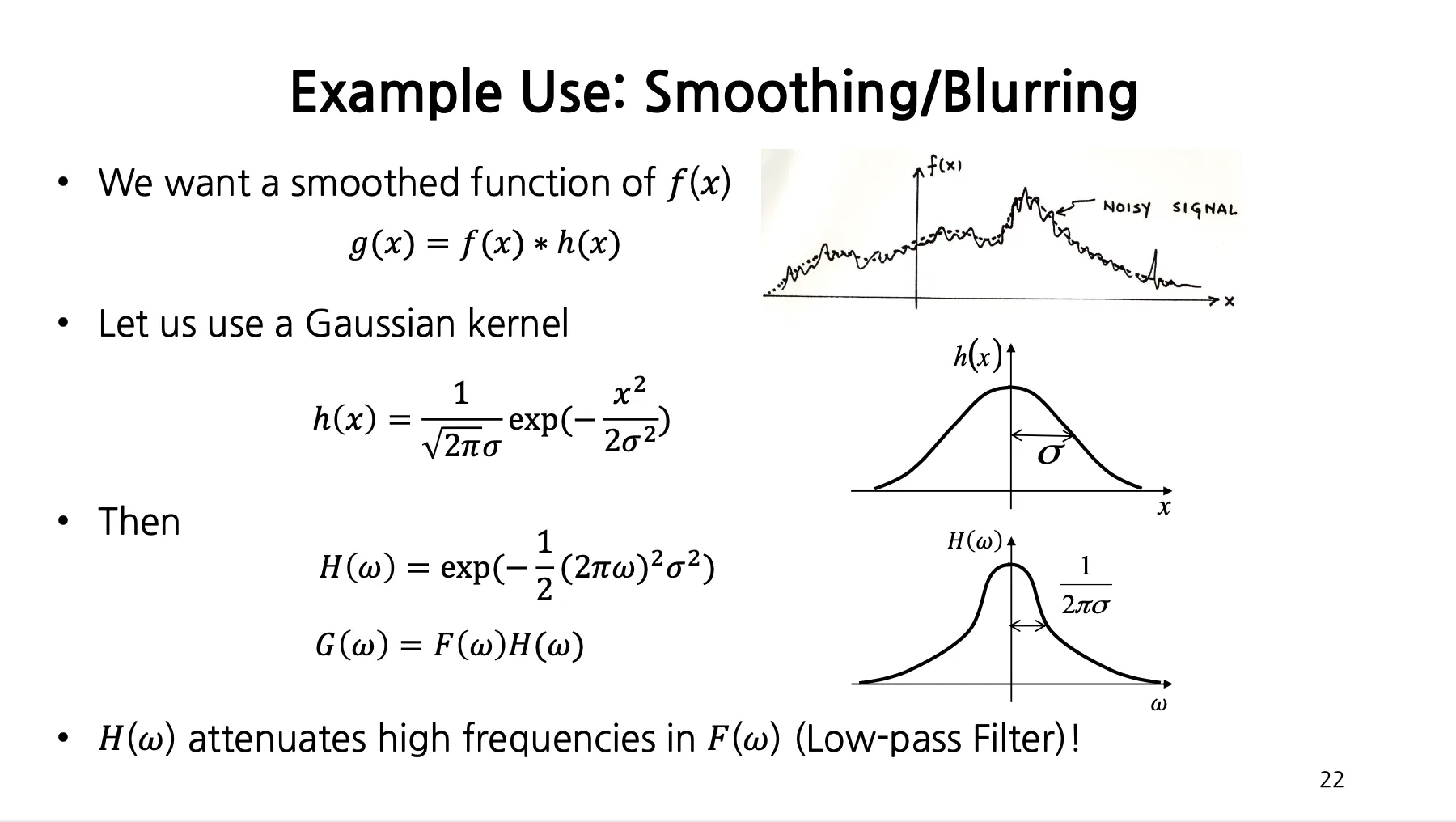
Example Use: Smoothing/Blurring

•
f(x)f(x) 의 smoothed function 이 필요할 때 Gaussian Kernel 을 사용.
•
h(x)=12πσexp⁡(−x22σ2)h(x) = \frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{x^2}{2\sigma^2})
•
H(ω)=exp⁡(−12(2πω)2σ2)H(\omega) = \exp(-\frac{1}{2}(2\pi\omega)^2\sigma^2)
•
Gaussian Kernel 은 Frequency Domain 에서 Low-Pass Filter 로 적용. → Smoothing 효과

2-D Fourier Transform

•
1-D Fourier Trasnsform, Inverse Fourier Transform
F(ω)=∫−∞∞f(x)exp⁡(−iωx)dxF(\omega)=\int_{-\infty}^{\infty}f(x)\exp(-i\omega x)dx
f(x)=12π∫−∞∞F(ω)exp⁡(iωx)dωf(x) = \frac{1}{2\pi}\int_{-\infty}^\infty F(\omega)\exp(i\omega x)d\omega
•
2-D Fourier Transform, Inverse Fourier Transform
F(u,v)=∫−∞∞∫−∞∞f(x,y)exp⁡(−i(xu+yv))dxdyF(u,v)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x,y)\exp(-i(xu+yv))dxdy
f(x,y)=12π∫−∞∞∫−∞∞F(u,v)exp⁡(i(xu+yv))dudvf(x,y) = \frac{1}{2\pi}\int_{-\infty}^\infty\int_{-\infty}^\infty F(u,v)\exp(i(xu+yv))dudv
•
2-D Discrete Fourier Transform, Inverse Fourier Transform
F(u,v)=1MN∑m=0M−1∑n=0N−1f(m,n)exp⁡(−i(muM+nvN))F(u,v)=\frac{1}{MN}\sum_{m=0}^{M-1}\sum_{n=0}^{N-1}f(m,n)\exp(-i(\frac{mu}{M}+\frac{nv}{N}))
f(m,n)=1MN∑m=0M−1∑n=0N−1f(u,v)exp⁡(i(muM+nvN))f(m,n)=\frac{1}{MN}\sum_{m=0}^{M-1}\sum_{n=0}^{N-1}f(u,v)\exp(i(\frac{mu}{M}+\frac{nv}{N}))

Frequency Spectrum

•
2-D Fourier Transform 을 진행하고 나온 F(u,v)F(u,v) 는 Complex 형태.
•
F(u,v)F(u,v) 를 시각화하는 4 가지 방법이 있음.
◦
Complex Spectrum
F(u,v)=R(u,v)+iI(u,v)F(u,v) = R(u,v) +iI(u,v)
◦
Magnitude Spectrum
∣F(u,v)∣=R(u,v)2+I(u,v)2|F(u,v)|=\sqrt{R(u,v)^2 + I(u,v)^2}
◦
Phase Spectrum
ϕ(u,v)=tan⁡−1(I(u,v)/R(u,v))\phi(u,v)=\tan^{-1}(I(u,v)/R(u,v))
◦
Power Spectrum
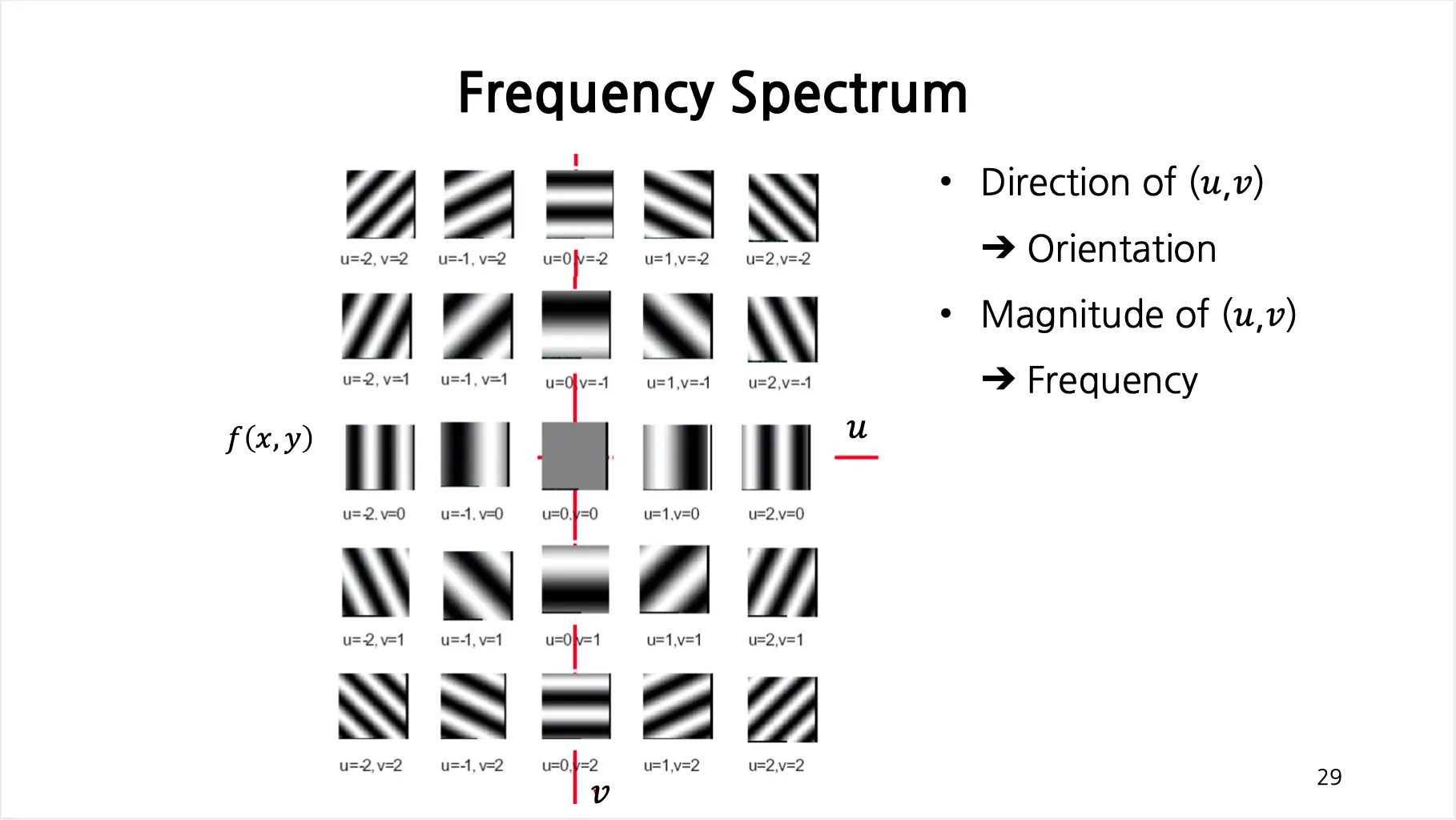
P(u,v)=∣F(u,v)∣2=R(u,v)2+I(u,v)2P(u,v) = |F(u,v)|^2 = R(u,v)^2 + I(u,v)^2
•
시각화 예시
◦
(u,v)(u,v) 의 방향 → 무늬의 방향
◦
(u,v)(u,v) 의 크기 → 무늬의 빈도

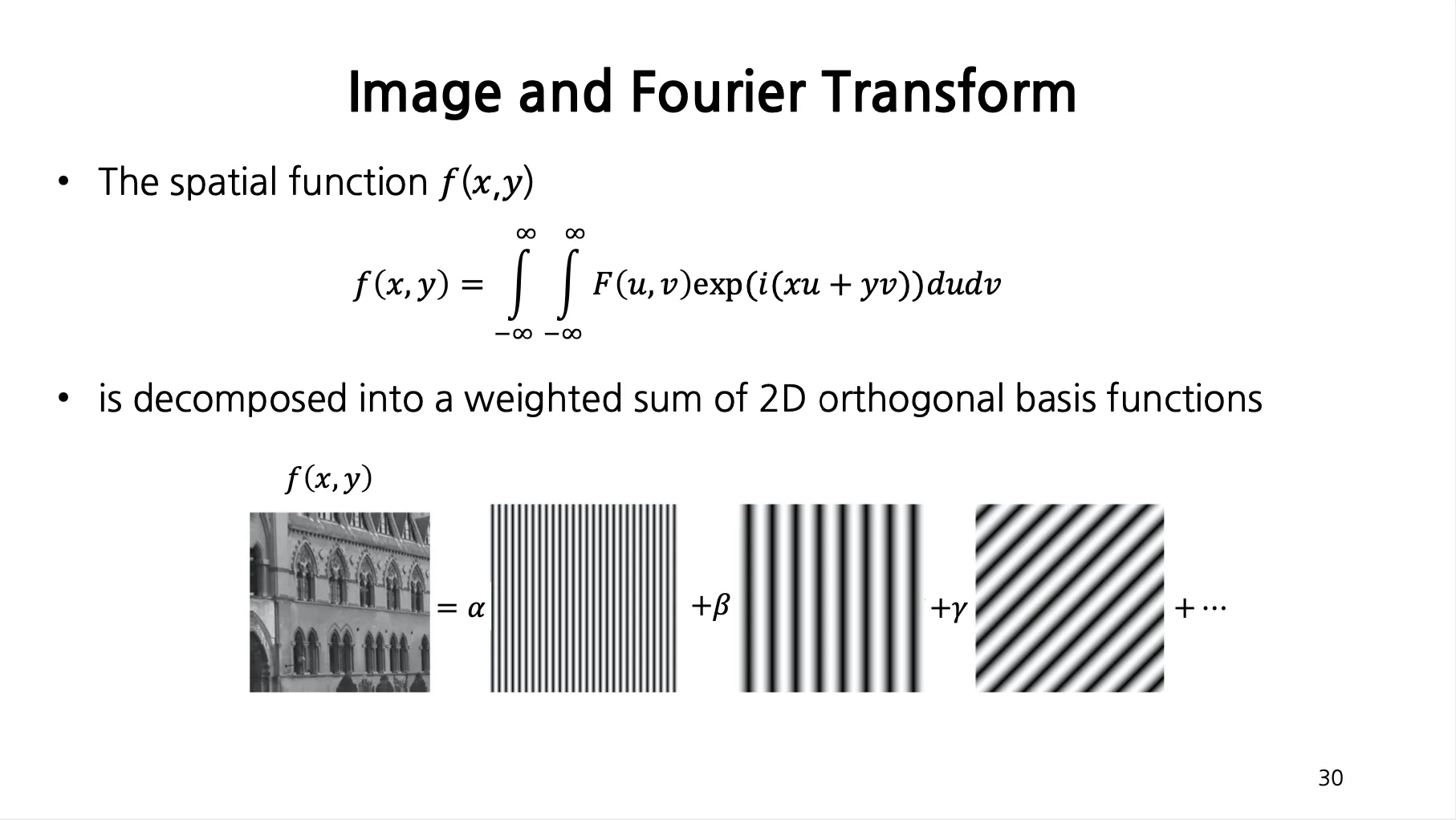
Image and Fourier Transform

•
Spatial Function 인 이미지 f(x,y)f(x,y) 에 2-D Fourier Transform 을 적용하면 다양한 종류의 frequency component 의 weighted sum 으로 나타낼 수 있음.

Image Processing in the Fourier Domain

•
이미지를 Fourier Transform 으로 변환하여 얻어낸 F(u,v)F(u,v) 의 크기를 (u,v)(u,v) 좌표에 표현.
•
인간이 만들어낸 반복된 구조물에 특정 방향성의 패턴이 검출되기도 함.
•
Gaussian Filter Convolution 의 시각화
•
Low-Pass Filtering & High-Pass Filtering
◦
Low-Pass Filtering 은 low frequency term 만 남기는 필터링이며 전체적으로 흐릿한 이미지를, High-Pass Filtering 은 high frequency term 만 남기는 필터링이며 Edge 가 강조된 이미지만을 남김.
•
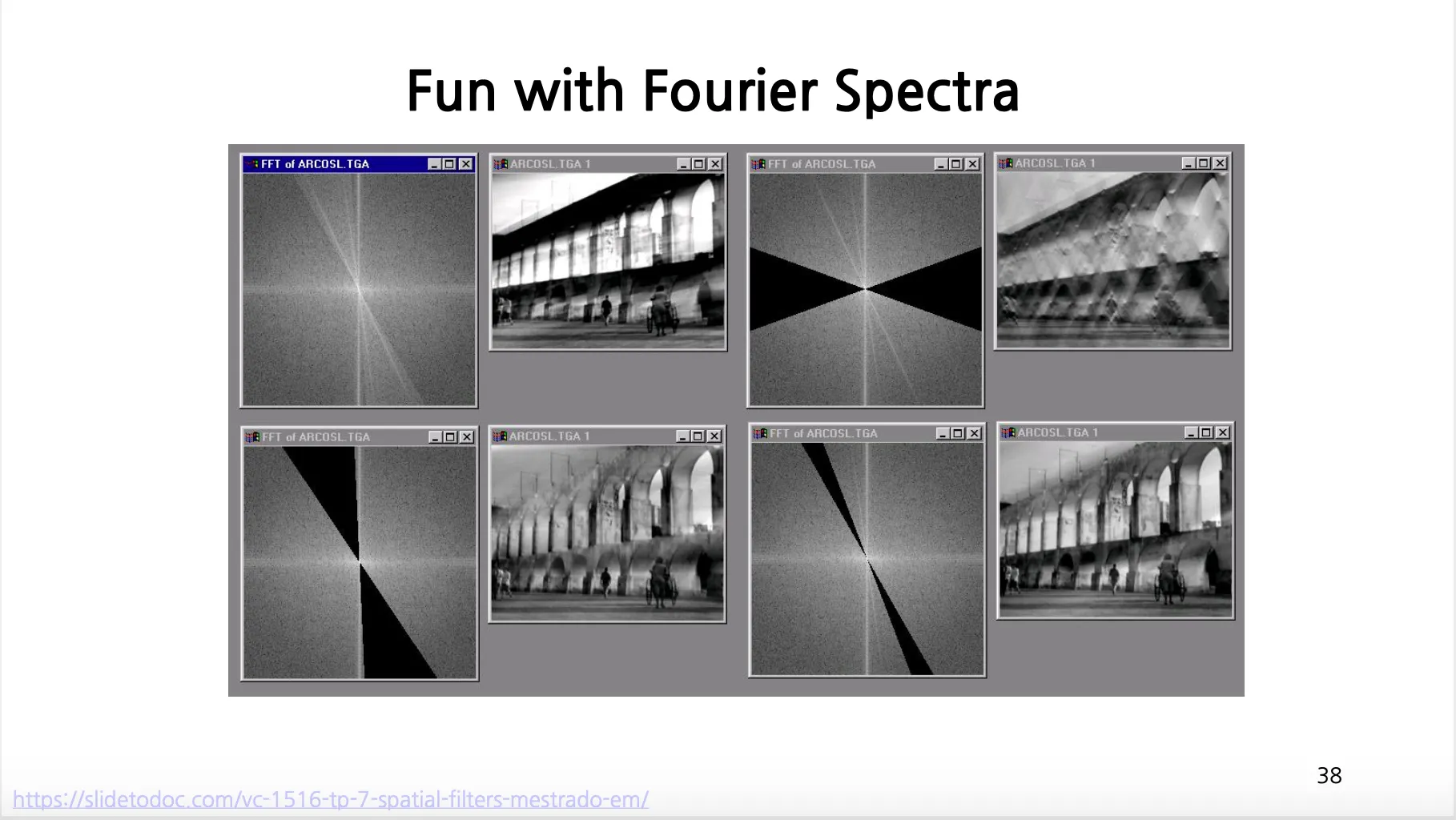
Frequency Domain 에서 여러 조작을 통해 다양한 이미지를 얻을 수 있음.
◦
특정 컴포넌트를 없애보면서 해당 컴포넌트들이 이미지의 어느 부분에 어떤 작용을 하는지 알 수 있음.