Duplicate

Lecture 17 | Stereo I - Epipolar Geometry

수강 일자
2022/11/01

Recovering 3D from Images

•
이미지로부터 3차원 정보를 알아내는 것
•
한 장의 이미지만으로는 공간상의 어느 지점을 보는 것인지 불확실하기 때문에 (structure and depth 관점에서) multi-veiw geometry 가 필요함.

Visual Cues for 3D

•
다양한 정보들의 도움으로 2차원 정보만으로 3차원 정보를 예측할 수 있음
•
Shading
◦
그림자 정보를 통해 어느 것이 더 뒤에있는지 알 수 있음
•
Texture
◦
동일한 패턴의 사이즈같은 것을 통해서 depth 정보를 알 수 있음
•
Focus
◦
선명하고 흐릿한 부분의 차이를 통해서 depth 의 다름을 알 수 있음 → 일부러 강조하여 3차원첢 보이게 하기도 함
•
Motion
◦
움직이는 물체를 찍은 연속적인 사진을 통해서 각 부분에 대한 정보를 얻을 수 있음
•
Others
◦
Highlights
◦
Shadows
◦
Silhouettes
◦
Inter-reflections
◦
Symmetry
◦
Light Polarization
◦
…
•
Shape from X
◦
X = shading, texture, focus, motion …
◦
3차원 정보를 다른 visual cues 로부터 알아내는 컴퓨터비전의 연구분야

Stereo Reconstruction

•
두 개의 이미지로부터 Shape 을 만들어내는 문제
•
이미지 두 개는 눈이 2개인 것이서 착안함
◦
눈이 하나 있는 것보다는 두 개 있는 것이 나음 (하나가 fail 되었을 떄도 대응 가능)
◦
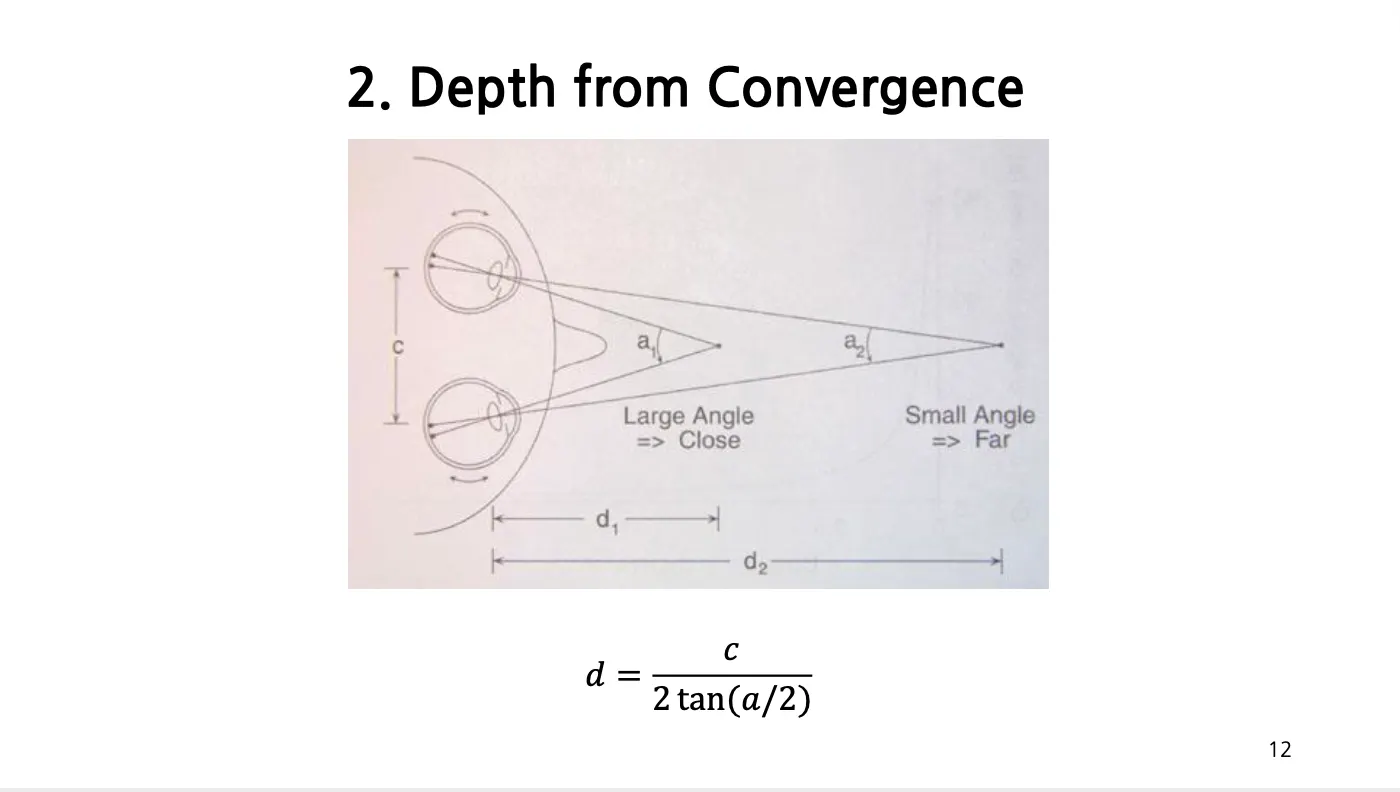
두 눈에서 얻은 정보를 바탕으로 거리 정보를 연산해낼 수 있음
▪
cc 는 두 눈 사이의 거리
▪
aa 는 물체를 볼 때 두 눈이 바라보는 방향의 각도
d=c2tan⁡(a/2)d= \frac{c}{2\tan(a/2)}
◦
두 눈을 이용해 disparity 를 계산할 수 있음
▪
DIsparity 는 오른쪽 눈에 맺힌 초점이 평소상태의 초점보다 이동한 거리 - 왼쪽 눈에 맺힌 초점이 평소상태의 초점보다 이동한 거리 를 나타냄 (거리의 + 는 우측, 거리의 - 는 좌측으로의 이동을 의미함)
▪
PP 는 근육을 쓰지 않고 자유롭게 두었을 때 눈이 바라보는 지점
▪
PP 보다 가까운 지점 CC 를 바라보았을 때 좌측 눈은 상이 기존보다 왼쪽에, 우측 눈은 상이 기존보다 우측에 맺히게 됨. → disparity 는 양수
▪
PP 보다 먼 지점 FF 를 바라보았을 때 좌측 눈은 상이 기존보다 왼쪽에, 우측 눈은 상이 기존보다 우측에 맺히게 됨. → disparity 는 음수

Stereo Photography and Stereo Viewers

•
초기에는 눈 좌측에 붉은색 필터, 우측에 푸른색 필터를 적용한 안경을 쓰고 영화를 보면 좌측 눈에는 붉은색 부분만, 우측 눈에는 푸른색 부분만 보여서 좌우측 눈의 정보에 약간의 괴리가 생기고 3D 정보로 인식하게 하는 방법론을 사용함
•
최근에는 편광으로 된 안경을 사용해 좌우측 이미지에 괴리를 줌 (disparity 에 따라 거리감을 느끼는 인간의 눈의 성질을 이용함)
•
Additional) Disparity 로부터 3차원 정보를 구성하는 방법론은 다음시간에 배움

Estimating Depth with Stereo

•
Stereo: Shape from motion between two views
◦
카메라의 motion (다른 viewpoint) 을 통해서 3차원 정보를 복원하는 문제
•
Camera pose 에 대한 정보와 Corresponding point 에 대한 정보를 고려해야 함.
•
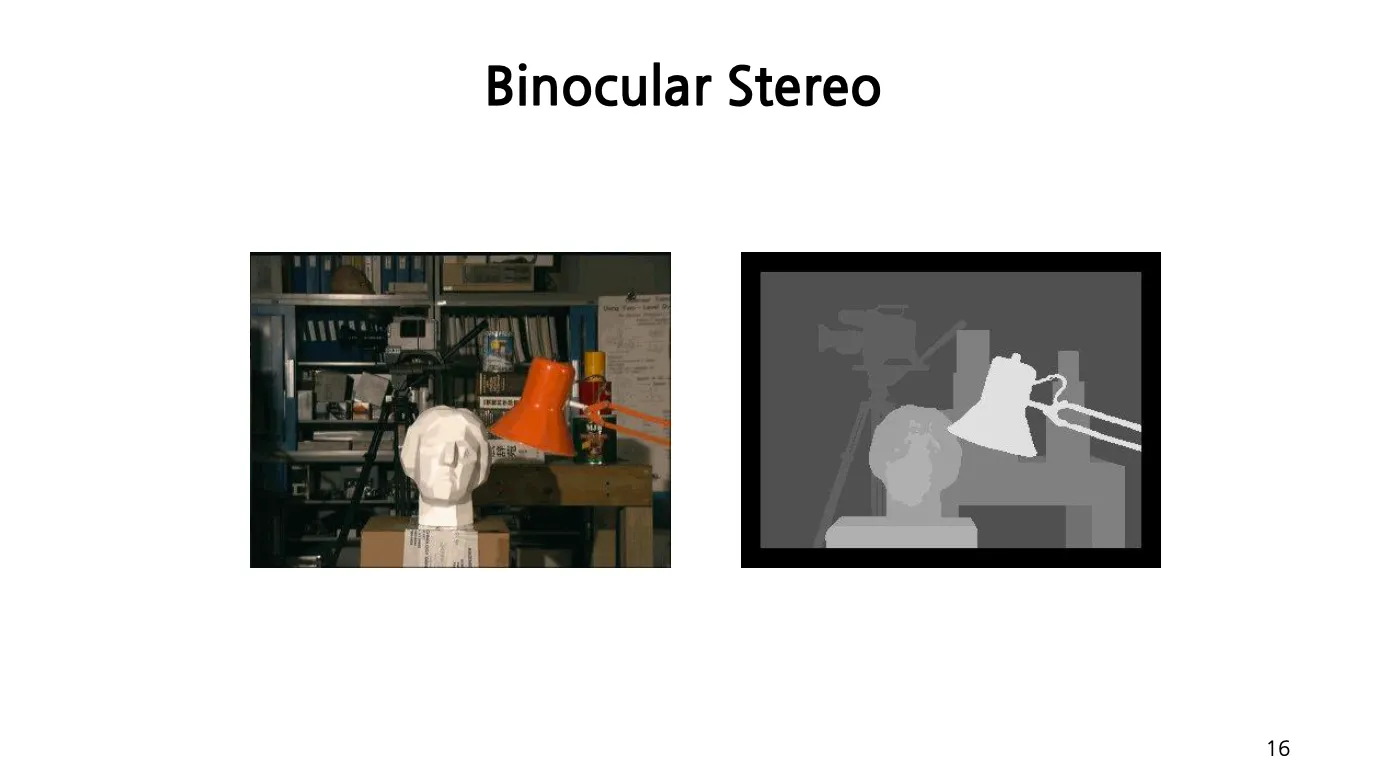
가까이 있을 수록 많이 움직인다는 정보를 통해서 depth map 을 얻을 수 있음.

Depth from Binocular Stereo

•
어떤 scene point 가 두 장의 이미지 속에서 어느 지점에 해당하는지를 알면, 그것을 통해 depth 정보를 알아낼 수 있는데 기본적인 방법이 triangulation 임
•
Scene point 와 두 optical center 사이에 삼각형을 정의할 수 있음

Epipolar Geometry: Notation

•
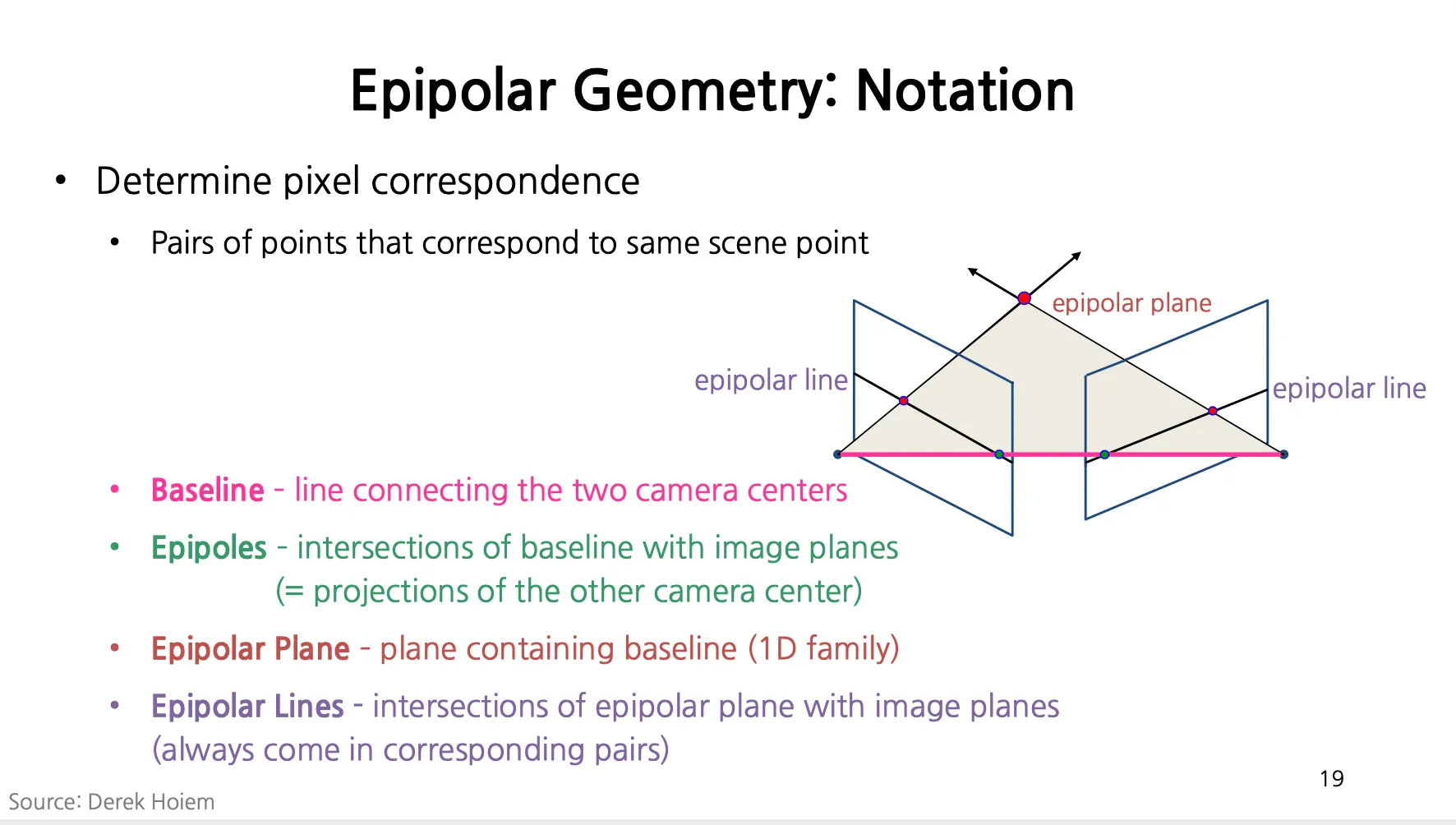
Baseline: 두 카메라의 center 를 연결한 선
•
Epipoles: Image plane 과 basline 이 만나는 점들 (projection of the other camera center)
•
Epipolar Plane: Scene point 와 camera center 들로 정의되는 plane
•
Epipolar Lines: Epipolar Plane 과 Image Plane 사이의 intersection line

Epipolar Constraint

•
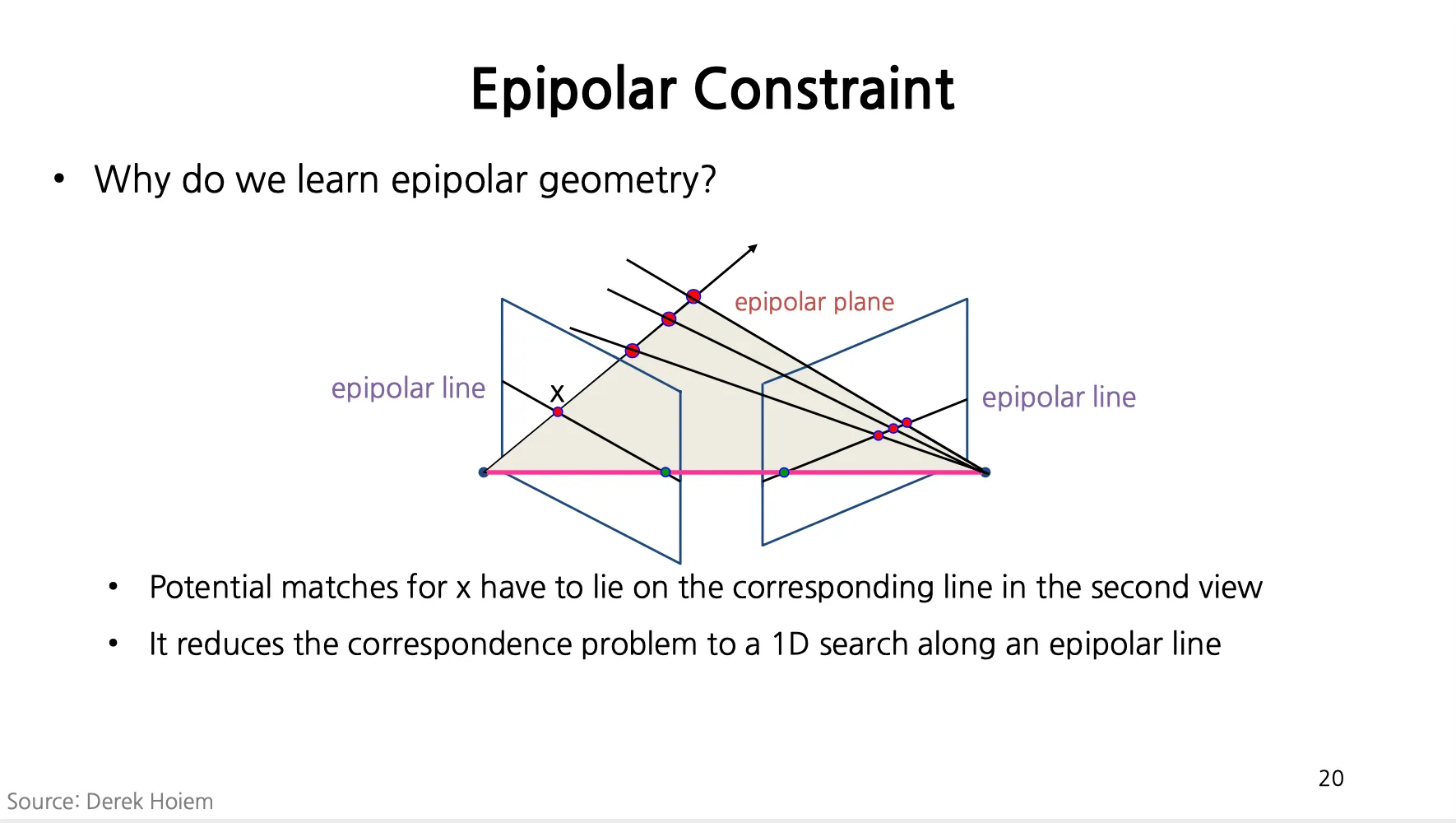
특정 이미지에 맺힌 점의 corresponding point 는 다른 이미지 위의 epipolar line 위에 있음
◦
첫 번째 이미지와 해당 이미지의 camera center 다른 이미지와 다른 이미지의 camera center 가 주어지면 첫 번째 이미지의 특정 점에 대한 epipolar line 을 찾을 수 있음!
•
Search 문제를 2D (Image Plane) 에서 1D (Epipolar Line) 로 낮춤

What do the Epipolar Lines Look Like?

•
Converging Cameras
◦
모든 Epipolar line 은 Epipole 을 지나기 때문에, Epipolar line 들은 epipole 로 수렴하게 됨.
◦
Converging Camera 는 Epipole 이 이미지 상 (Image Plane) 에 존재함 (이미지 내에 있다는 이야기는 아님)
•
Parallel Cameras
◦
Baseline 과 Image Plane 이 평행하여 만낮 않기 때문에, 그 교점인 Epipole 은 무한대 지점에 있음.

Stereo Geometry, with Calibrated Cameras

•
Calibration 이 된 camera → Intrinsic, Extrinsic Parameter 를 다 아는 camera
•
한 camera reference frame 에서 에서 다른 camera reference frame 으로 변환
X′=RX+TX' =RX +T \\
•
Epopolar Plane 에 대한 normal (T,X′T, X' 가 Epipolar Plane 위에 있으므로)
T×X′=T×RX+T×T=T×RXT\times X' = T\times RX + T \times T = T \times RX
•
양쪽에 X′X' 에 대한 dot product 를 하면,
X′⋅(T×X′)=X′⋅(T×RX)=0X' \cdot (T\times X')=X' \cdot (T\times RX) = 0
◦
X′X', RXRX, TT 는 같은 평면 (Epipolar Plane) 위에 존재함
•
위 식을 skew-symmetric matrix 와 substitution 을 이용해 다음과 같이 변형할 수 있음.
◦
E=[Tx]RE = [T_x]R 는 Essential Matrix
X′⋅(T×RX)=0X′⋅([Tx]RX)=0X′TEX=0X'\cdot (T\times RX) = 0 \\ X' \cdot ([T_x]RX) = 0 \\ X'^TEX = 0

Essential Matrix Example: Parallel Camera

•
Parallel 한 camera 의 경우 한 이미지의 특정 점과 대응되는 점은 다른 이미지와 같은 horizontal line 위에 놓여 있음을 알 수 있음.
•
Essential Matrix 를 이용하면 Corresponding Point 가 어디 있는지를 찾는데 추가적인 정보를 얻을 수 있음.

Fundamental Matrix

•
Camera 가 더 이상 canonical (Intrinsic Parameter Matrix 가 Identity)하지 않을 때의 일반적인 표현
•
KK 와 K′K' 가 두 camera 의 Intrinsic Parameter
pc=K−1ppc′=K′−1p′p_c = K^{-1}p\\ p_c' = K'^{-1}p'
•
Essential Matrix formula 는 다음과 같이 변형됨
pc′TEpc=0→p′TK′−TEK−1p=0F=K′−TEK−1=K′−T[Tx]RK−1p_c'^T Ep_c = 0 \rarr p'^TK'^{-T}EK^{-1}p = 0 \\ F = K'^{-T}EK^{-1} = K'^{-T}[T_x]RK^{-1}
◦
FF 를 Fundamental Matrix 라고 함.
•
FF 는 기본적으로 Essential Matrix EE 와 유사함.
◦
Corresponding Points 와 Epipolar Line 간의 관계를 나타내줌.
◦
Essential Matrix 는 camera coordinate 기준이라면, Fundamental Matrix 는 pixel coordinate 기준임.
•
Fundamental Matrix FF 를 알고 있다면, Corresponding Point 끼리의 관계를 p′TFp=0p'^TFp =0 이라는 식으로 정의했기 떄문에, 하나의 point 와 FF 를 알고 있다면 그에 대응되는 point 에 대한 constraint 로 사용할 수 있음. (실제로 FF 는 pp 라는 point 가 어디에 위치하는지를 몰라도 Extrinsic, Intrinsic Parameter 만 알면 구할 수 있음.)

Eight-Point Algorithm

•
Essential, 혹은 Fundamental Matrix 를 구하는 알고리즘
•
8 개 쌍의 Corresponding Points 를 찾고 Least Square Solution 을 적용할 수 있음.
•
pi′TFpi=0p_i'^T Fp_i =0 이기 때문에 pi′p_i' 와 pip_i 의 각 쌍당 식을 1개 만들 수 있고 FF 의 DOF 인 8 개의 쌍이 필요함
[uiui′,vi′ui,ui,ui′vi,vivi′,vi,ui′,ui′,vi′,1][F11F12F13F21F22F23F31F32F33]=0\begin{bmatrix} u_iu_i', v_i'u_i, u_i,u_i'v_i,v_iv_i',v_i,u_i',u_i',v_i',1 \end{bmatrix} \begin{bmatrix} F_{11} \\ F_{12} \\ F_{13} \\ F_{21} \\ F_{22} \\ F_{23} \\ F_{31} \\ F_{32} \\ F_{33} \\ \end{bmatrix} = 0
•
At=0At=0 문제이므로 AA 에 SVD 를 적용한다음에 smallest eigenvalue 를 가진 eigenvector 를 뽑는 형태로 풀 수 있음.

Basics - Cross Product

c=a×b=[a2b3−a3b2a3b1−a1b3a1b2−a2b1]=[0−a3a2a30−a1−a2a10][b1b2b3]=[a]×b\begin{align*} c &= a\times b = \begin{bmatrix} a_2b_3 - a_3b_2 \\ a_3b_1 - a_1b_3 \\ a_1b_2 - a_2b_1 \\ \end{bmatrix} \\ &= \begin{bmatrix} 0 & -a_3 & a_2\\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \\ \end{bmatrix} \begin{bmatrix} b_1 \\ b_2 \\ b_3 \\ \end{bmatrix} \\ &= [a]_{\times}b \end{align*}
•
[a]×[a]_{\times} 는 skew-symmetric matrix