Incremental Structure-from-Motion
•
Input: Images, Output: 3D Points, Camera Poses
•
기존의 TK Factorization 방법과는 다르게 Orthogonal Camera Assumption 이 없어도 됨.
◦
Camera Parameters 를 이용함.
•
온전한 Point Trajectory 가 없어도 됨.
•
Occlusion 이 있어도 무관함.
•
Large-Scale 에 대해서도 잘 동작함.
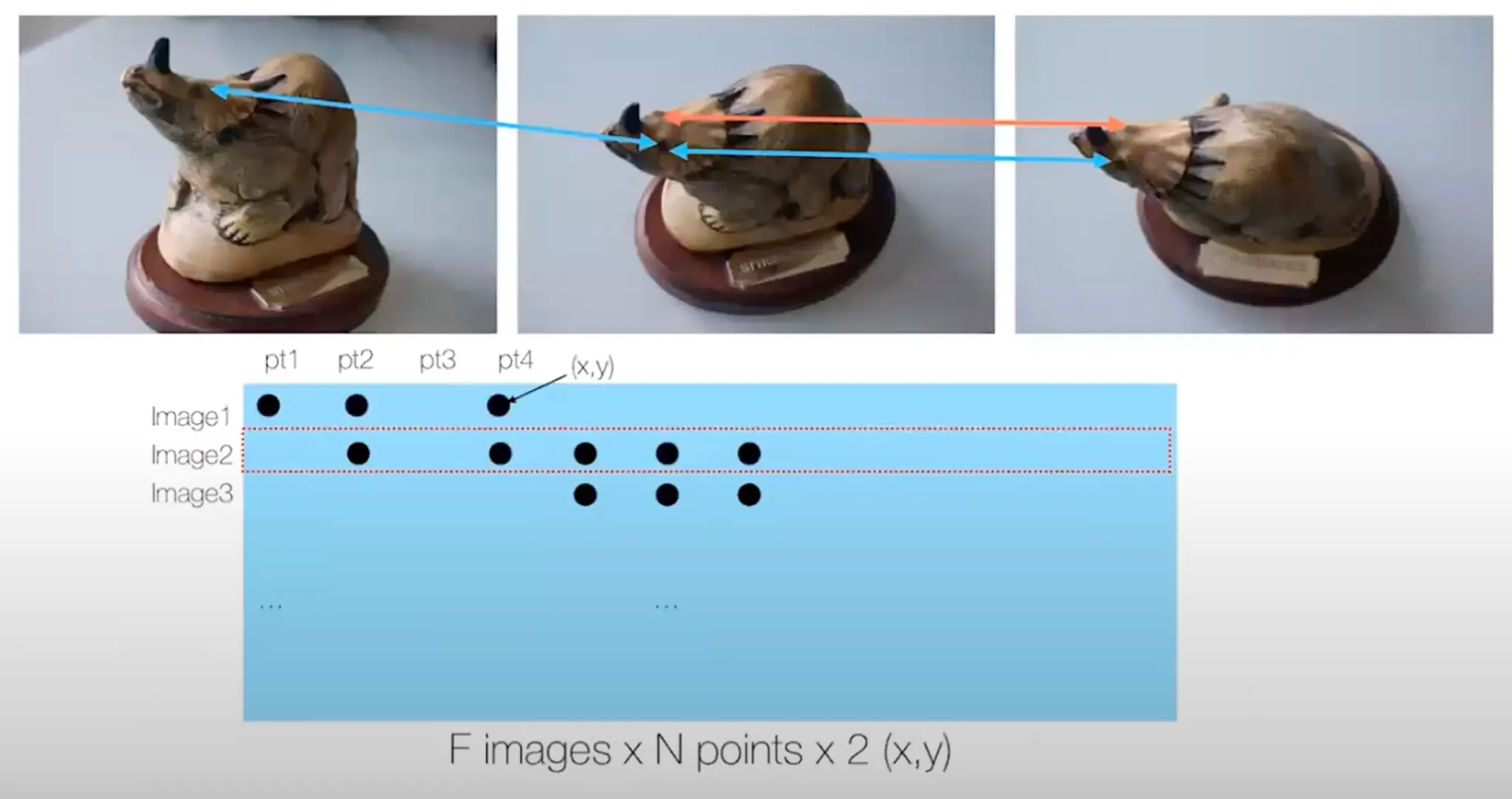
Step 1: Find Correspondences Across All Views
•
RANSAC with Essential (Fundamental) Matrix 을 거쳐 Corresponding Points 의 outlier 를 제거함.
◦
Homography 를 사용할 수 있는 경우는 Pure Rotation Camera 와 Planar Scene 일 때 뿐이라서, 이 경우에는 일반적인 경우에 적용 가능한 Essential (Known ) 및 Fundamental Matrix 를 사용해 Mapping 을 구해야 함.
◦
임의의 5 Points (for Essential Matrix) Algorithm 을 이용해 를 유추할 수 있고, 5 Points 의 선택을 반복하면서 inlier 수가 많은 5 Points 를 찾아 해당 세팅을 기준으로 나머지 outlier 를 버림.
•
이후, 각 이미지에서 Corresponding Points 를 찾은 뒤, 동일한 점을 나타내는 이미지의 픽셀값들을 같은 열이 되도록 위와 같이 구성할 수 있음.
Step 2: Choose the First Two (good) Images
•
Multiview 중 좋은 두 개의 view 를 찾는 과정
•
좋은 view 는 다음과 같은 특징들을 의미함.
◦
충분한 Corresponding Points 의 존재
◦
충분한 거리가 있는 Baseline (Camera Center 의 거리) → Depth Variation 을 적게하기 위함.
•
위 조건을 만족해보이는 두 쌍의 view 에 대해서 correspondence 로 를 구하고 decompose 하여 camera pose 를 구한 다음에, triangulation 을 사용해 3D point 의 위치를 찾고 reprojection error 를 구해 이 값이 작은 것을 추가적으로 찾음.
◦
에서 camera pose 로 가능한 4 가지 중 선택하기 위해서 triangulation 으로 Point Cloud 를 만들어보고 valid 한 points (points in front of camera) 의 수 (Cheriality) 가 가장 많은 것을 선택함.
•
이 과정까지 하면 두 개의 view 와 해당 view 들로 생성한 Point Cloud 를 얻은 상태임.
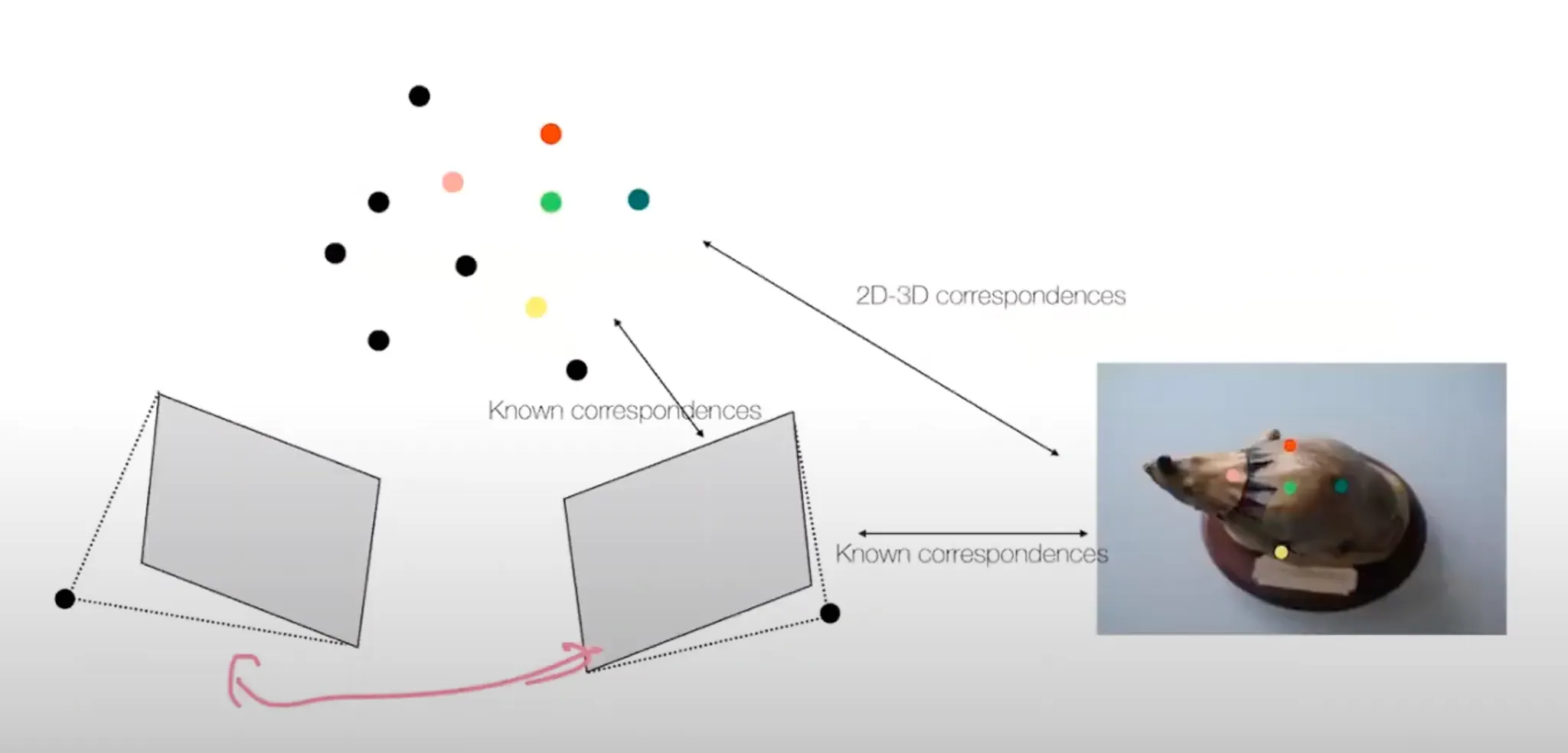
Step 3: Register the Next Image
•
세 번째 view 가 추가될 때, 두 번째 Image 위의 point 와 세 번째 Image 위의 point 사이의 correspondence 와 두 번째 Image 와 3D Point 와의 correspondence 를 알고 있기 때문에 3D Point 와 세 번째 Image 사이의 correspondence 를 알 수 있음.
•
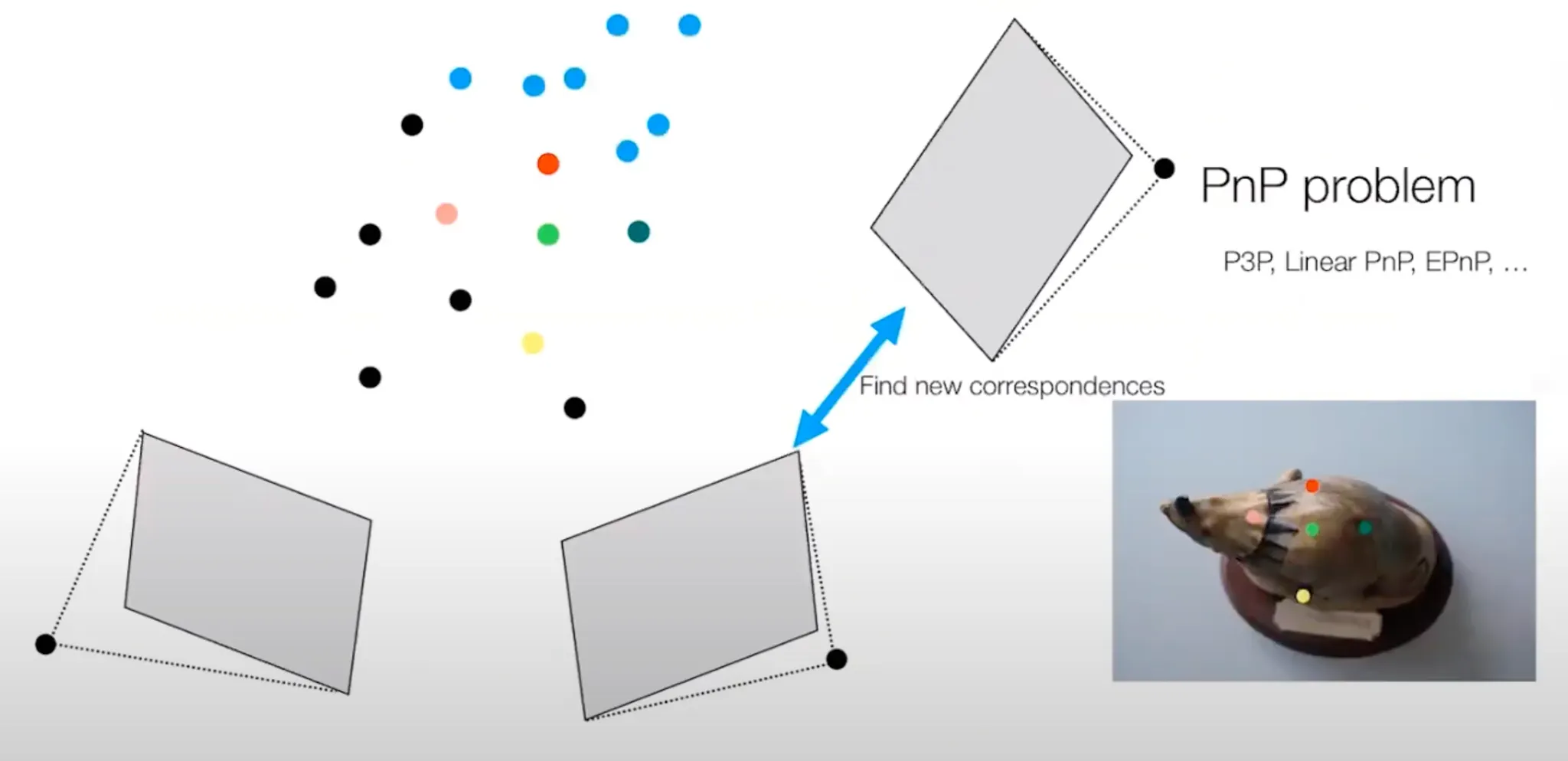
3D - 2D correspondence 를 바탕으로 PnP 방법론을 적용하면 세 번째 Image 의 Camera Pose 를 얻어낼 수 있음. 이 때, P3P 를 사용한다고 하면 임의의 세 점을 선택하여 Camera Matrix 를 구해보고 reprojection error 를 구하는 것을 반복하여 outlier 가 가장 적은 세 점의 세팅을 찾고 해당 세팅에서 outlier 를 제거한 채 남은 점들로 PnP 를 사용해 최종 를 구하게 됨.
•
PnP 이후 Non-Linear Optimization 으로 를 한 번 더 optimize 할 수도 있고, 최종 로부터 를 decompose 해냄.
•
이 과정을 보통 Registering Camera, Stitching View 등으로 부름.
•
이 과정까지 하면 세 번째 view 의 camera pose 까지 얻어낼 수 있음.
Step 4: Triangulate Additional 3D Points
•
앞선 두 개의 view 에서 occlusion 으로 연결되지 않았던 correspondence 가 세 번째 view 가 추가되면서 생겼을 수도 있기 때문에 다시 또 3D points 들을 triangulate 해야 함.
•
View 가 추가될 때, 그 이전에 추가된 모든 view 와의 pair correspondence 를 기반으로 새로운 point 들을 찾음. → 점점 view 를 추가하는 과정 때문에 Incremental SfM 이라고 불림.
Step 5: Bundle Adjustment
•
새로운 view 를 추가하는 것은 point 의 위치를 바꿀 수도 있는데, 이 과정은 다시 또 (PnP 로 인해) 기존에 존재했던 view 에 대응되는 camera pose 를 바꾸게 되고 camera pose 가 바뀌게 되면 또 (triangulation 에 의해) 3D point 가 또 바뀔 수가 있음. (서로 엮여있음…)
•
이 모든 것을 한 번에 optimize 하는 과정이 Bundle Adjustment 임.
•
이 과정은 위의 식에서 처럼 camera pose matrix 와 point cloud 를 기반으로 projection 된 point 와 measure 한 point 와의 reprojection error 에 대한 항목을 Non-Linear Optimization 을 사용해 최소화하는 방향으로 진행할 수 있음.
◦
다만, 이 과정은 굉장히 computation cost 가 큼… (적어도 GPU 등이 없던 과거에는…)
◦
다행인 점은, Jacobian Matrix 가 생각보다 sparse 하다는 점임.
▪
특정 점을 움직일 때 특정 camera pose 에서 보이지 않아서 영향이 없는 경우나, 특정 카메라를 움직일 때 특정 점은 아예 안보여서 영향이 없는 경우가 있음.
▪
실제로는 거의 Jacobian Matrix 는 diagonal matrix 처럼 등장함.
•
때문에 또한 diagonal 에 가깝고, optimization 에 가 쓰이는데 이 계산이 굉장히 빠름.
•
놀라운 점은 나 Camera Distortion 또한 모르더라도 같이 Bundle Adjustment 최적화 식에 포함되어 있기 때문에 estimate 할 수도 있음.