EfficientNet

분야
Scaling Up Methodology
리뷰 날짜
2021/08/01
본 포스트에서는 Model Scaling 을 새로운 방법으로 해석하여 성능에 큰 향상을 불러온 논문에 대해서 알아보려고 합니다. 리뷰하려는 논문의 제목은 다음과 같습니다.
“EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks”
논문에 대한 내용을 직접 보시고 싶으신 분은 이곳을 참고하시면 좋습니다.

Objective

논문의 배경은 Convolutional Neural Network 가 좋은 성능을 얻기 위한 접근으로 Scaling-Up 이 자주 사용되던 트렌드로부터 시작합니다. 실제로 2016 년에 등장한 ResNet 은 ResNet-18 에서 ResNet-200 으로 네트워크의 깊이를 늘림으로써 scaling-up 을 진행했고, 2018 년에 등장한 Gpipe 는 baseline 모델을 4배 정도 키워서 ImageNet top-1 accuracy 84.3% 를 달성했습니다.
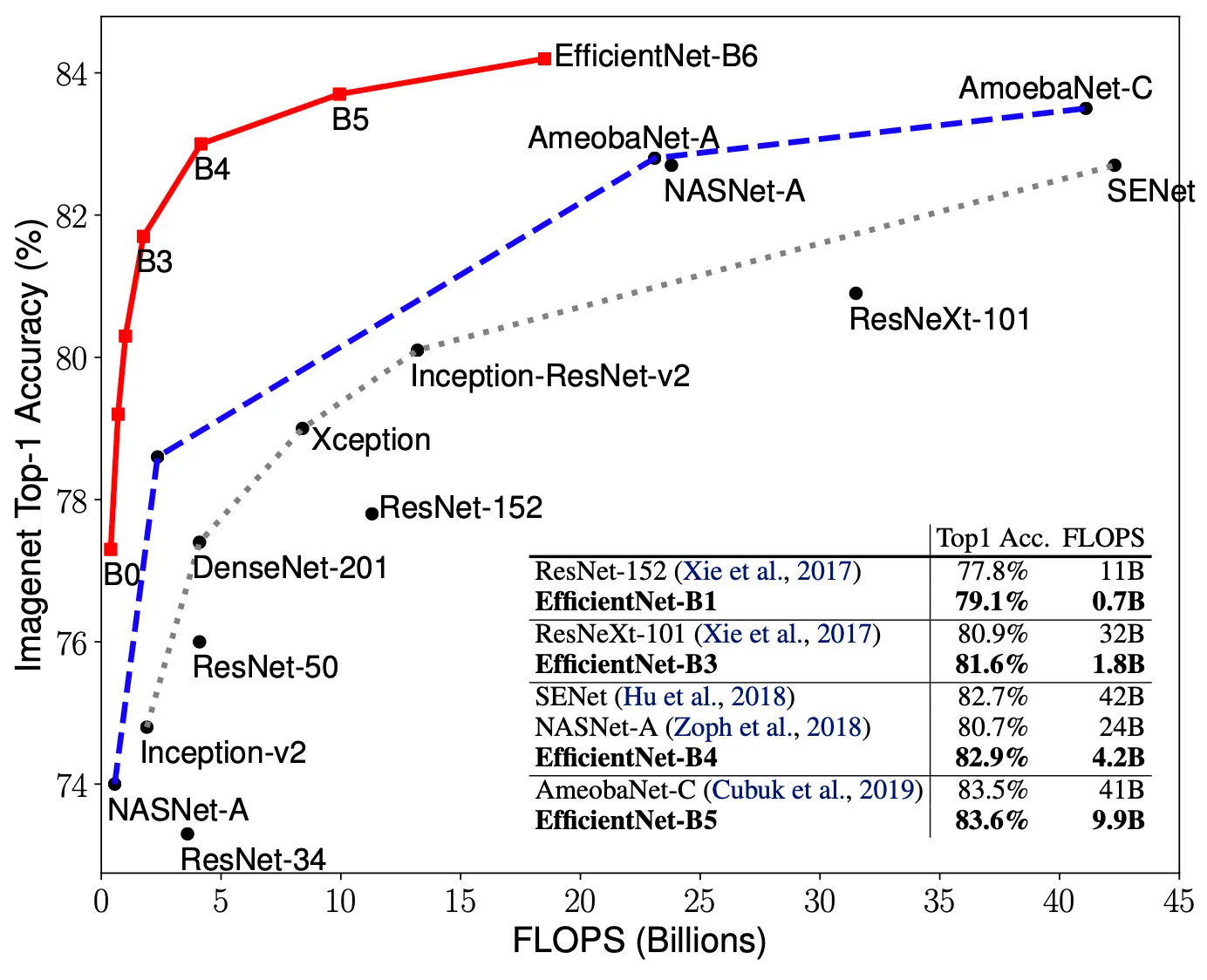
Scaling-Up 이 네트워크의 성능을 향상시킨다는 것은 기존의 많은 연구들에 의해서도 잘 알려져 있는 사실입니다. 위 그 그래프처럼 네트워크의 parameter 수가 증가함에 따라서 ImageNet top-1 accurcay 가 증가하는 양상도 이런 일반적인 사실을 뒷받침합니다.
하지만, Scaling-Up 을 통해 네트워크의 성능을 향상시키는 방법론의 문제점은 Scaling-Up 을 했을 때 성능이 향상될 것이라는, 통계적으로 뒷받침되는 일반적인 관점을 제외하면 얼마나, 어떻게, 무엇을 Scaling-Up 해야 최적의 네트워크 구조가 형성될지에 대한 정보가 전혀 없다는 것입니다. 이러한 점은 기존의 논문들이 단순히 깊이(depth), 너비(width), 이미지 크기(resolution) 중 한 가지에만 집중하여 Scaling-Up 을 했던 이유이기도 합니다. 두 가지 이상의 요소를 동시에 조절하여 최적의 값을 찾아내는 것은 사실상 불가능하다는 것입니다.
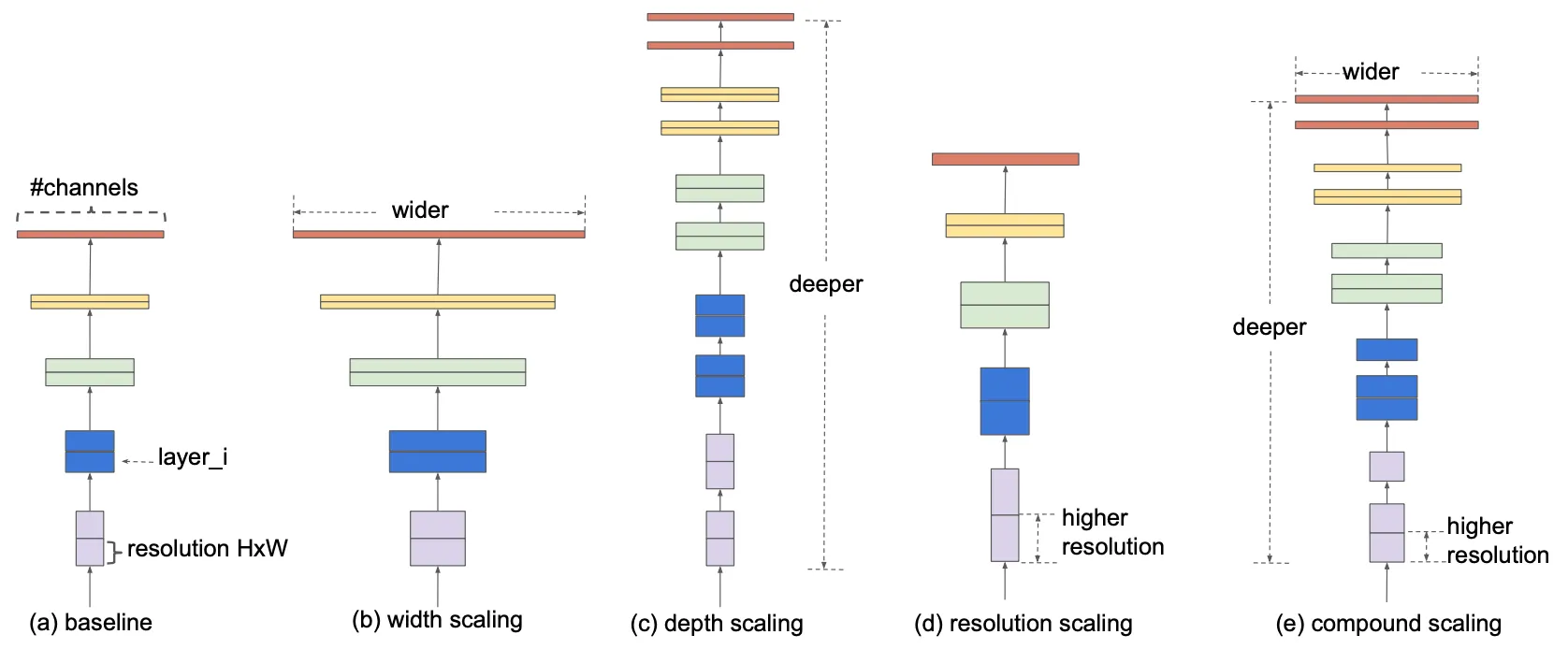
위 그림의 (b), (c), (d) 는 각각 너비, 깊이, 이미지 크기를 Scaling-Up 하는 형태로 성능을 향상해온 기존 네트워크들의 방법론을 시각화한 것입니다. 반면 논문에서는 위에서 언급한, 기존에 Scaling-Up 을 할 때 사용하던 방법을 개선하려는 시도를 합니다. 단순히 한 가지 요소만을 Scaling-Up 하여 제한적으로 성능을 향상시켰던 것에서 벗어나 세 가지 요소(네트워크의 깊이, 너비, 그리고 이미지 크기)를 포함한 어떠한 원칙을 찾아서 적절하게 Scaling-Up 을 할 수 있지 않을까에 대한 물음을 던진 것입니다. 그것이 (e) 에서 시각화된 것이며, 그 방법론을 정형화하려는 것이 논문의 목적입니다.

Compound Model Scaling

논문에서 정의한 문제를 이해하기 위해서는 먼저 간단한 개념인 FLOPS 에 대한 이해가 필요합니다.
FLOPS (FLoating point OPerationS) 란? 글자에서 찾아볼 수 있는 것처럼 네트워크가 가지는 부동소수점 연산의 수입니다. 보통 CPU 의 성능을 나타내는데 사용하나, 논문에서는 한정된 자원에서의 성능 최적화를 목적으로 했기 때문에 한정된 연산 수를 기반으로 최대 FLOPS 를 설정하여 구성했습니다. 단, 보통의 경우에는 FLOPs 와 FLOPS 를 구별하여 사용하는데, 전자는 네트워크가 가지는 부동소수점 연산 수로, 후자를 초당 행할 수 있는 부동소수점의 연산 수로 정의하지만 논문의 내용 상 FLOPS 라고 표기했지만 FLOPs 의 의미를 가지는 것을 알 수 있습니다.
지금부터 논문에서 정의한 문제에 대해서 알아보려고 합니다.

Problem Formulation

먼저, 하나의 layer 연산을 다음과 같이 정의할 수 있습니다.
Yi=Fi(Xi)Y_i=\cal{F_i}\it({X_i} )
여기서 Fi\cal{F_i} 가 layer 의 연산이자 operator 이고 XiX_i 는 입력 텐서로 ⟨Hi,Wi,Ci⟩\left\langle H_i, W_i, C_i \right\rangle 의 dimension 을 가지며, HiH_i 와 WiW_i 는 텐서의 spatial dimension 을, CiC_i 는 텐서의 channel dimension 을 의미합니다. 이러한 기본적인 layer 연산의 수학적인 표현을 사용해, Convolutional Neural Network 의 연산 전체를 나타내면 다음과 같습니다.
N=Fk⊙...⊙F2⊙F1(X1)\cal{N}=F_k\odot...\odot F_2\odot F_1(\it{X_1})
여기서, ⊙\odot 은 합성함수 연산으로 보시면 됩니다. 이에 따라서 위 식을 일반화하여 간단히 나타내면,
⨀i=1...sFiLi(X⟨Hi,Wi,Ci⟩)\bigodot_{i=1...s}\cal{F_i^{\it{L_i}}}(\it{X_{\left\langle H_i, W_i, C_i \right\rangle}})
위와 같은 식으로 표현할 수 있습니다.
LiL_i 는 일반적으로 Convolutional Neural Network 에서 반복되는 stage 를 나타내는 요소입니다. 정확히 말씀드리자면, stage ii 에서 layer FiF_i 가 LiL_i 번 반복되는 것을 나타냅니다.
기존의 식에서 stage number 로 인덱싱했던 입력 텐서(XiX_i) 또한 그 dimension 을 직접적으로 명시해주는 형태(X⟨Hi,Wi,Ci⟩X_{\left\langle H_i, W_i, C_i \right\rangle})로 변환하여 적어놓은 것입니다.
위에서 수학적으로 표현한 네트워크의 연산을 사용해 논문에서는 앞서 말씀드렸던 것처럼 깊이, 너비, 그리고 이미지 크기에 따른 최적화를 진행합니다.
이 때, 깊이는 LiL_i, 너비는 CiC_i, 이미지 크기는 Hi,WiH_i, W_i 에 관련 있는 항목임을 알 수 있습니다. LiL_i 가 늘어남은 곳 반복되는 layer 의 수가 많아짐을 의미하고, CiC_i 가 늘어남은 계산에 사용될 kernel 의 channel 수가 많아져야 함을(너비의 증가) 의미하고, Hi,WiH_i, W_i 가 늘어남은 입력텐서의 spatial dimension 인 이미지의 크기가 늘어남을 의미하기 때문입니다.
즉, 논문에서는 기존의 연구들이 특정 기능을 가장 잘 수행하는 네트워크 구조 (및 연산) 인 Fi\cal{F_i} 를 찾으려고 했던 것과는 달리 고정된 baseline Fi\cal{F_i} 에 대해서 최적화된 Li,Ci,Hi,WiL_i,C_i,H_i,W_i 를 찾으려는 시도를 합니다. 다만, 모든 stage 및 layer 에 대해서 Li,Ci,Hi,WiL_i,C_i,H_i,W_i 를 하나하나 최적화하는 것은 최적화 작업이 고려해야 할 범위를 매우 넓히기 때문에 논문에서는 모든 layer 가 같은 비율로 scaling 된다는 가정하에 최적화를 진행하게 됩니다.
이러한 논문의 생각을 다음과 같은 optimization problem 으로 정의할 수 있습니다.
max⁡d,w,r Accuracy(N(d,w,r))s.t N(d,w,r)=⨀i=1...sFi^d⋅Li^(X⟨r⋅Hi^,r⋅Wi^,w⋅Ci^⟩)Memory(N)≤target_memoryFLOPS(N)≤target_flops\begin{align*} \max_{d,w,r}\ &\rm{Accuracy}(\cal{N}(d,w,r))\\ s.t\ & \cal{N}(d,w,r) = \bigodot_{i=1...s}\cal{\hat{F_i}^{\it{d\cdot\hat{L_i}}}}(\it{X_{\left\langle r\cdot \hat{H_i}, r\cdot \hat{W_i}, w\cdot \hat{C_i} \right\rangle}}) \\ & \rm{Memory}(\cal{N})\le \rm{target\_memory} \\ & \rm{FLOPS}(\cal{N})\le \rm{target\_flops} \end{align*}

Scaling Dimensions

지금까지 논문에서 정의한 문제에 대해서 알아보았습니다. 하지만, 정의한 문제에서 어려운 점은 높이, 너비, 이미지 크기 각각이 다르게 가지는 리소스의 제약 아래에서 서로가 서로에게 의존적일 수 있는 d,w,rd, w, r 을 찾아내는 것입니다. 앞서도 언급했지만 이러한 어려움 떄문에 기존의 많은 Convolutional Neural Network 의 연구들은 이 중 한 가지만을 scaling 하는 형태로 연구를 진행했습니다.

Depth(d)

네트워크의 깊이(depth) 를 Scaling-Up 하는 것은 많은 Convolutional Neural Network 에서 사용했던 방법입니다. 이러한 시도들은 깊은 네트워크가 풍부하고 복잡한 특성들을 추출할 수 있으며 새로운 작업에 대해서 일반화가 잘된다는 직관에 기반한 것들입니다. 하지만, 자연스럽게도 네트워크의 깊이가 깊어지면서 gradient vanishing 문제가 나타났고, ResNet 과 Batch Normalization 에서 해당 문제들을 해결하는 방법론을 적용해 해당 문제점을 완화했었습니다. 그럼에도 ResNet-1000 은 ResNet-101 에 비해서 비슷한 성능을 보였습니다.
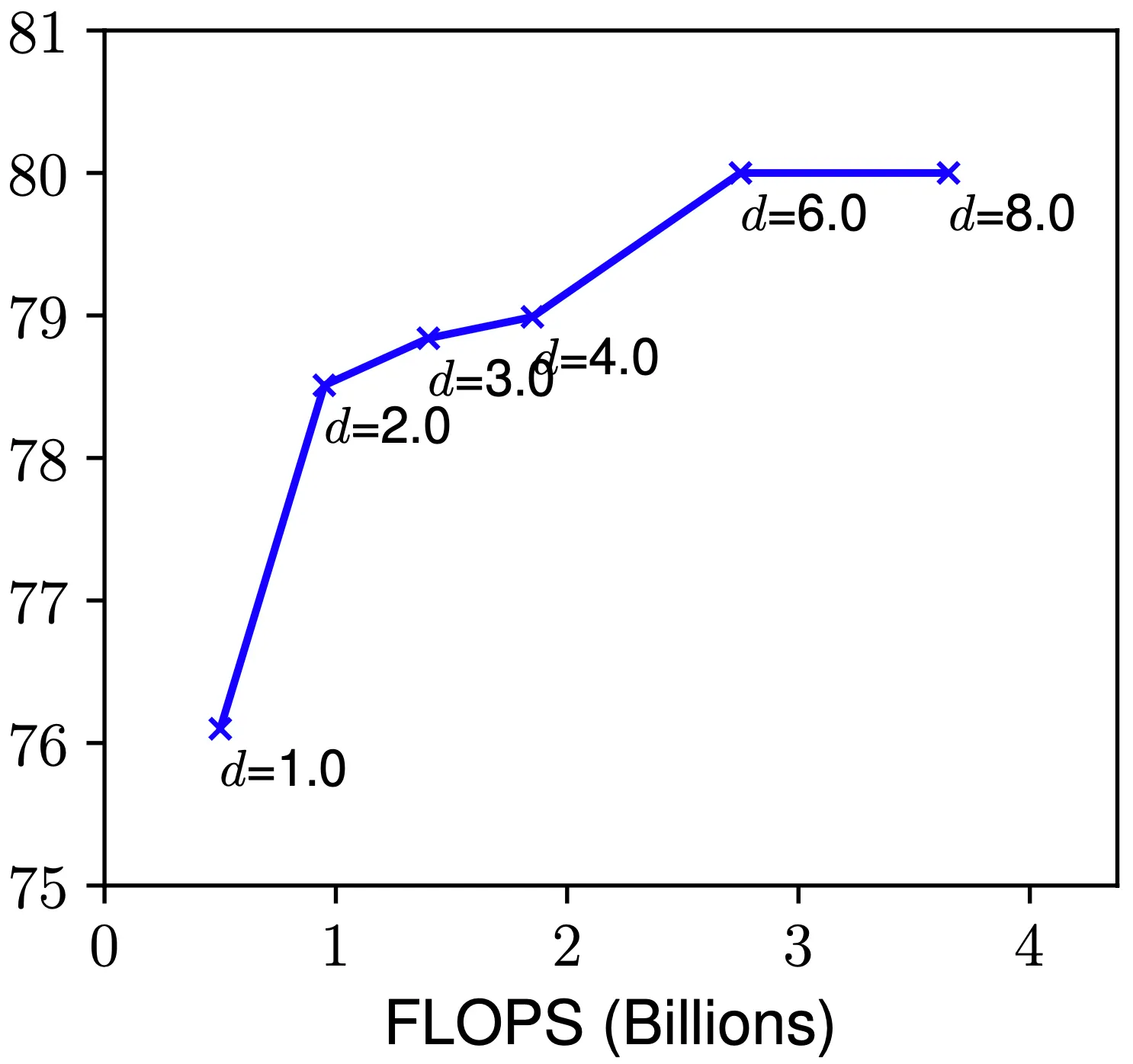
실제로 논문에서는 baseline 네트워크의 dd 값을 변화시켜 가면서 네트워크의 성능을 측정해보았습니다. 그 결과 위의 그림과 같이 일반적으로는 dd 값이 증가함에 따라 네트워크의 성능도 증가했지만, 어느 시점 이후부터는 미비한 성능 향상, 혹은 오히려 성능이 감소하는 시점이 온다는 것을 알 수 있었습니다.

Width(w)

네트워크의 너비(depth) 를 Scaling-Up 하는 것은 비교적으로 작은 크기의 네트워크들에서 사용했던 방법입니다. 실제로, Wide Residual Networks 에서는 넓은 네트워크가 상대적으로 이미지의 세밀한 특성을 추출할 수 있고 학습이 용이했다는 결과를 보인 적이 있습니다. 하지만, 매우 넓고 깊이가 얕은 네트워크의 경우에는 high-level features(복잡한 특성) 를 학습하기 어렵습니다.
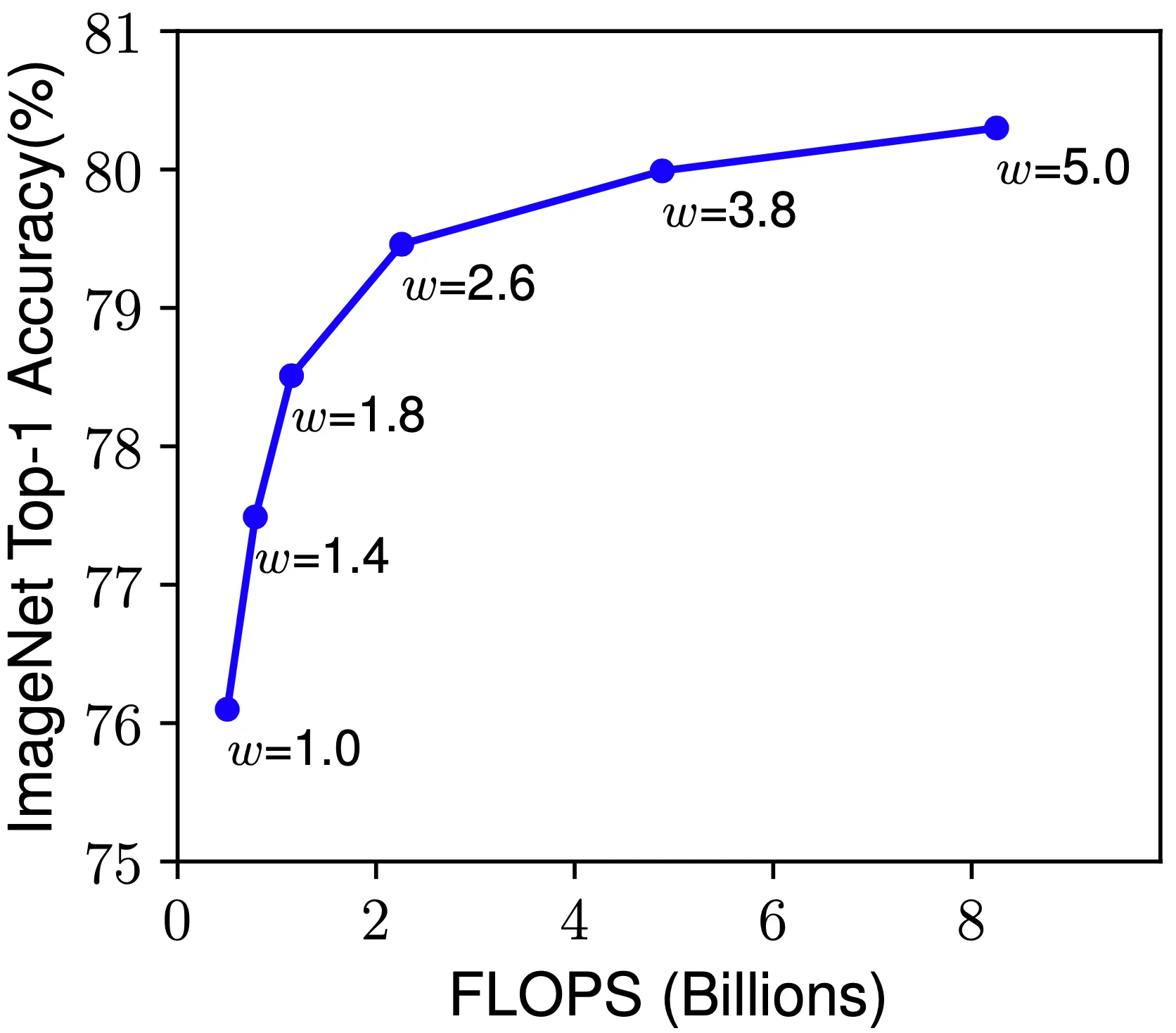
마찬가지로 논문에서는 baseline 네트워크의 ww 값을 변화시켜 가면서 네트워크의 성능을 측정해보았습니다. 그 결과 위의 그림과 같이 일반적으로는 ww 값이 증가함에 따라 네트워크의 성능도 증가했지만, 어느 시점 이후부터는 성능향상이 포화되는 것을 확인할 수 있었습니다.

Resolution(r)

네트워크의 이미지 크기(resolution) 를 Scaling-Up 하는 것은 잠재적으로 네트워크가 이미지의 세밀한 패턴을 추출할 수 있게 했습니다. 초기 224×224224\times224 형태의 이미지 크기를 가지던 Convolutional Neural Network 부터, Inception-v4 에서는 229×229229\times229 형태의 이미지를, Zoph et al. 에서는 331×331331\times331 형태의 이미지를 사용했습니다. 최근 들어서는 Gpipe 가 480×480480\times480 형태의 이미지를 사용하여 ImageNet 을 사용한 SOTA 를 달성했고, object detection 분야에서는 600×600600\times600 형태의 이미지도 종종 사용되고 있습니다.
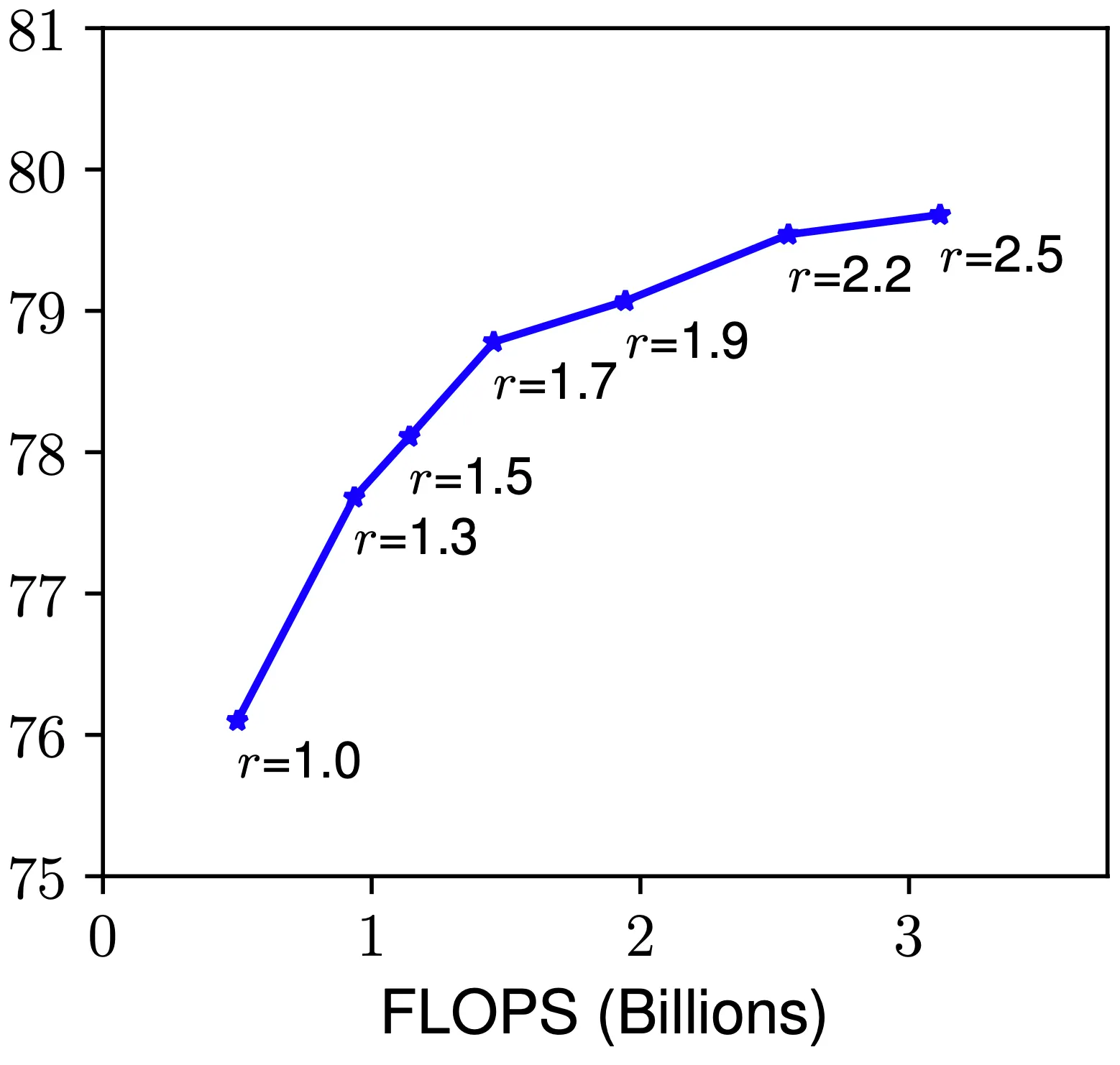
하지만, 마찬가지로 논문에서는 baseline 네트워크의 rr 값을 변화시켜 가면서 네트워크의 성능을 측정해보았습니다. 그 결과 위의 그림과 같이 일반적으로는 rr 값이 증가함에 따라 네트워크의 성능도 증가했지만, rr 값의 증가로 얻는 성능 증가량이 점점 적어지는 모습을 볼 수 있었습니다.
여기서 논문의 첫 번째 관찰을 제시합니다.
네트워크의 dimension 의 어떤 요소라도 Scaling-Up 을 하면 성능을 증가시킬 수 있지만, 이러한 방식으로 얻는 성능 증가는 네트워크가 커질수록 사라져간다는 사실을 실험적으로 확인합니다.

Compound Scaling

위에서 네트워크의 dimension scale 각각이 독립적이지 않다는 사실을 실험적으로 알 수 있었습니다.
직관적으로, 큰 이미지 크기를 사용하는 네트워크에 대해서는
1.
비슷한 특성을 가지는 특성들끼리 잘 모아줄 수 있는 큰 receptive field 를 가지는 것이 유리하기 때문에 depth 가 깊어야 함
2.
커진 이미지 속에서 세밀한 패턴을 찾기 어려워졌기 때문에 그에 도움이 되는 width 가 넓어야 함
을 알 수 있습니다.
이러한 직관은 기존의 single-dimension scaling 에서 벗어나 균형있게 각 dimension 요소들을 Scaling-Up 해야할 필요성을 제안해줍니다.
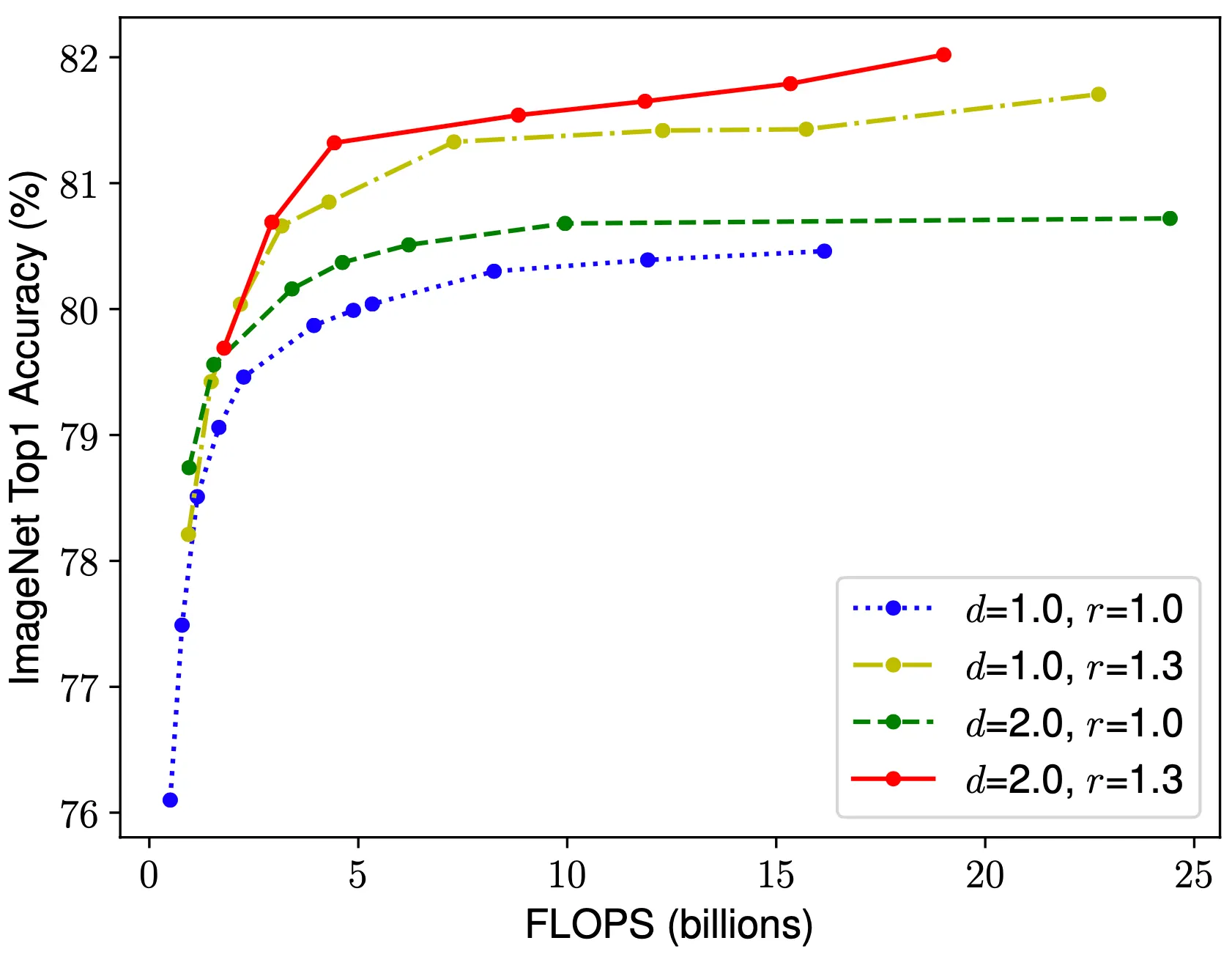
이러한 직관을 실험적으로 증명해보이기 위해서 논문에서는 d,rd, r 을 고정시킨 채 ww 를 변화시켜가면서 측정한ImageNet top-1 accuracy 의 변화를 제시합니다. 그 결과 고정시킨 d,rd, r 값이 모두 큰 경우에 대해서 전체적으로 성능이 좋았음을 볼 수 있었습니다. 이 결과가 시사하는 바는 하나의 dimension scale 에 대해서 최적의 값을 찾았더라도, 다른 dimension 의 조절을 통해서 충분히 더 좋은 값을 찾을 수 있다는 것입니다.
여기서 논문의 두 번째 관찰을 제시합니다.
더 높은 성능 향상을 위해서는 네트워크의 모든dimension (깊이, 너비, 이미지 크기) 의 균형 맞춘 Scale-Up 이 중요하다는 사실을 실험적으로 확인합니다.
실제로, Zoph et al. 과 Real et al. 에서 이미 임의로 네트워크의 너비와 깊이를 balancing 하는 작업을 진행했지만, 이는 수동으로 튜닝해야하는 지루하고 어려운 과정이 필요했습니다.
논문에서는 이를 개선할 수 있는 새로운 compound scaling method 를 제시합니다.
depth:d=αϕwidth:w=βϕresolution:r=γϕs.t. α⋅β2⋅γ2≈2α≥1,β≥1,γ≥1\begin{align*} \rm{depth:} &\it{d=\alpha^\phi}\\ \rm{width:} &\it{w=\beta^\phi}\\ \rm{resolution:} &\it{r=\gamma^\phi}\\ \rm{s.t.\ } &{\alpha\cdot\beta^2\cdot{\gamma}^2\approx2}\\ &{\alpha\ge1, \beta\ge1, \gamma\ge1}\\ \end{align*}
위 식에서 드러난 것 처럼, d,w,rd,w,r 을 compound coefficient 인 ϕ\phi 를 기반으로 동일한 비율로 scaling 하는 방법을 제시한 것입니다. 이 때 α,β,γ\alpha, \beta, \gamma 는 small grid search 를 사용해서 얻어내는 상수이고, ϕ\phi 는 리소스의 여유에 따라서 depth, width, resolution 에 분배하는 추가적인 리소스의 활용으로 해석할 수 있습니다.
Grid Search 란? Grid Search 는 말 그대로 격자 모양의 공간에서 값을 뽑아내서 해당 값으로 시도해보는 방법입니다. 흔히 deep learning 분야에서는 hyperparameter tuning 에 자주 사용하는 방법인데, 이 경우에는 α,β,γ\alpha, \beta, \gamma 의 3 개의 값이 존재하므로 3 차원 공간의 격자에서 점을 선택하여 그 값을 시도해보는 방법으로 볼 수 있습니다. 논문에서 small grid search 라고 한 것을 보아 대략 1 ~ 1.2 사이를 쪼개서 격자를 만든 이후에 시도해본 것으로 예상할 수 있을 것 같습니다. 뒤에서 나오겠지만, ϕ\phi 를 모르는데 어떻게 최적화된 값을 선택하는지에 대해서 궁금하실 분들을 위해 미리 알려드리자면, ϕ\phi 는 처음에 1로 고정 시켜둔 뒤에 small grid search 를 진행합니다.
왜 α⋅β2⋅γ2≈2{\alpha\cdot\beta^2\cdot{\gamma}^2\approx2} 라고 설정한 constraint 에서 α,β,γ\alpha, \beta, \gamma 의 승수가 다를까? 이는 d,w,rd, w,r 이 FLOPS 에 미치는 영향의 정도가 다르기 때문입니다. dd 의 경우에는 2 배의 증가가 단순히 같은 네트워크 연산의 한 번 더 반복이라서 FLOPS 의 2 배 증가로 이어지지만, w,rw, r 같은 경우에는 2 배의 증가가 convolution 연산에서 가로와 세로로 탐색해야 할 영역이 각각 2 배가 되기 때문에 FLOPS 의 4 배 증가로 이어지게 됩니다.
정리하자면, 위와 같은 방법론과 제약조건을 통해서 α,β,γ\alpha, \beta, \gamma 그리고 ϕ\phi 를 찾아 주어진 리소스 내의 최적의 네트워크 구성을 찾아내려는 시도를 합니다.

EfficientNet Architecture

네트워크의 dimension scaling 은 layer operation Fi^\cal{\hat{F_i}} 를 바꾸어 주지는 않기 때문에 논문에서는 좋은 baseline 네트워크를 설정하는 것이 중요했습니다. 특히, 논문에서는 그들이 제시한 scaling method 의 효율성을 잘 보여줄 수 있는 baseline 네트워크 설정에 목적을 두었고, 그렇게 만들어진 baseline 네트워크가 EfficientNet 입니다.
Tan et al. 의 네트워크 구조에 영감을 받아 구성한 EfficientNet 은 Tan et al. 과는 달리 optimization goal 을 설정할 때 latency 대신에 FLOPS 를 사용합니다. 이는 논문에서 목표로 했던 것이 특정한 하드웨어 구조에 기반한 것이 아니기 때문입니다. 논문에서 설정한 optimization goal 은 다음과 같습니다.
max⁡m(Accuracy(m)×[Flops(m)Target Flops]w)\max_m(\rm{Accuracy(m)}\times\rm{[\frac{Flops(m)}{Target\ Flops}]^{\it{w}}})
Accuracy 를 최대한 높이면서, Target Flops 에 대해서 실제 사용한 네트워크의 Flops 의 비율을 최소화하는 형태의 목적함수를 설계한 것입니다. 실제로 Accuracy 늘리기와 Flops 줄이기는 서로 trade off 관계에 있는 두 요소이기 때문에 이를 묶어서 하나의 지표로 만들었다고 보시면 됩니다. 이러한 설계의 바탕에는 ww 가 음수임이 포함되어 있고 실제로 -0.07 의 값을 사용했다고 합니다.
논문에서 사용한 baseline 네트워크는 특별히 EfficientNet-B0 으로 불립니다. 그 구조는 위와 같습니다. 기본적인 형태는 네트워크 설계에 참고한 Tan et al. 의 것과 비슷하지만, Target Flops 가 400M 으로 더 컸기 때문에 조금 더 큰 네트워크 구조를 설계했다고 합니다. 더불어 SENet 에서 사용한 squeeze-and-excitation optimization 을 적용했다고 합니다. 이는 다음 논문리뷰 때 자세히 알아보도록 하겠습니다.
MBConv block 이란? MBConv block 은 MobileNet-v2 에서 소개된 block 으로 흔히 알고 있는 ResNet 에서 사용하는 residual block 의 convolutional layer 의 너비를 변경해준 block 입니다. Residual block 에서 사용하는 1×11\times1 Conv → 3×33\times3 Conv → 1×11\times1 Conv 은 텐서가 각각 넓고, 얇고, 넓은 (Wide → Narrow → Wide) 의 구조로 변화하는데 비해 MBConv block 텐서가 각각 얇고, 넓고, 얇은 (Narrow → Wide → Narrow) 구조로 변화합니다. 이렇게 설계한 것은 skip connection 으로 narrow 한 tensor 를 전달해 주어 메모리 효율성을 높이기 위해서라고 합니다. 더불어, 중간단계의 넓은 텐서에 적용하는 Conv 가 depthwise convolution 연산입니다. Depthwise convolution 연산은 기존의 covolution 연산과는 다르게 kernel 의 channel 이 존재하지 않습니다. 즉, 채널 방향으로의 convolution 이 없고, 입력 텐서의 각각의 channel 별 결과를 단순히 쌓는 형태로 출력 텐서가 나타나게 됩니다. 때문에 채널 방향으로의 convolution 을 입력 텐서의 각각의 channel 에 대해서 수행한 것을 다 더하는 연산 자체가 삭제되어 압도적으로 연산 수를 줄일 수 있는 것입니다.
제시한 baseline EfficientNet-B0 를 가지고 논문에서는 scaling method 를 두 단계를 거쳐 시행합니다.
1.
ϕ=1\phi=1 로 고정시키고 resource 를 기존보다 두 배 사용 가능하게 설정한 뒤, α,β,γ\alpha, \beta, \gamma 를 small grid search 를 통해서 최적의 값을 찾아냅니다. EfficientNet-B0 에서는 α⋅β2⋅γ2≈2{\alpha\cdot\beta^2\cdot{\gamma}^2\approx2} 조건 아래에서 α=1.2,β=1.1,γ=1.15\alpha=1.2, \beta=1.1, \gamma=1.15 를 최적으로 값으로 찾아냈습니다.
2.
α,β,γ\alpha, \beta, \gamma 값을 고정시킨 뒤, ϕ\phi 값을 변화시켜 가면서 서로 다른 EfficientNet-B1 부터 B7 까지를 얻어냅니다. 이렇게 얻어낸
실제로 큰 네트워크에서 직접적으로 α,β,γ\alpha, \beta, \gamma 값을 직접적으로 찾아내는 방법이 더 좋은 성능을 낼 가능성도 있지만 이렇게 되면 더 넓은 범위에서 최적의 값을 찾아야 하고 이는 불가능하다싶이 비용이 많이 들기 때문에 위와 같이 두 개의 단계로 나누는 방법을 사용했다고 합니다.

Experiments

Scaling Up MobileNets and ResNets

논문에서는 가장 먼저 제시한 Scaling Method 에 대한 검증을 진행합니다. 그 방법으로 EfficientNet 이 아닌, 기존의 널리 사용되고 있는 MobileNet 과 ResNet 에 대해서 ImageNet dataset 에 대해 논문의 방법론을 적용해 Scaling 한 결과를 제시합니다.
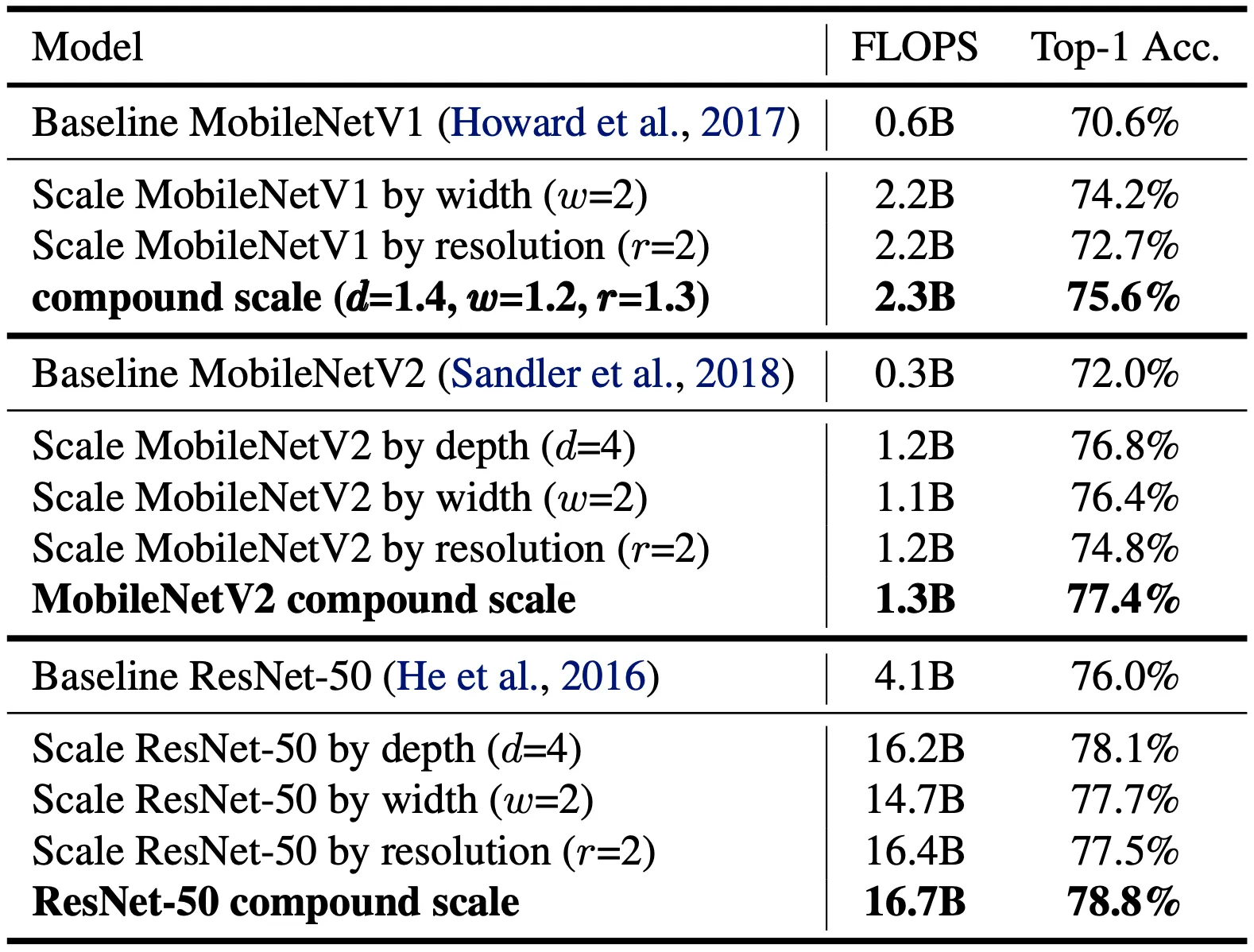
Howard et al. 의 MobileNet-v1, Sandler et al. 의 MobileNet-v2, He et al. 의 ResNet 이 실제로 baseline 네트워크로 사용되었고 세 baseline 네트워크 모두 하나의 dimension 을 사용해서 scaling 한 결과보다 유의미하게 증가한 top-1 accuracy 를 확인할 수 있었습니다. 이 결과가 논문의 방법론이 실제로 효과가 있음을 뒷받침한다고 주장합니다.

ImageNet Results for EfficientNet

다음으로, 논문에서는 앞서 설명했던, Tan et al. 을 기반으로 설계한 EfficientNet 을 이용해서 학습한 결과를 제시합니다. 그 전에, 논문에서는 학습에 사용한 네트워크의 구성에 대한 설명을 진행합니다. 이는 나열식으로 설명을 드리겠습니다.
1.
Optimization method 로 RMSProp 를 사용했습니다. decay factor 로 0.9 를, momentum 으로 0.9 를 사용했습니다.
2.
Batch Normalzation 을 사용했습니다. momentum 으로 0.99 를 사용했습니다.
3.
Weight decay(L2 Regularization) 로 1e−51e-5 를 사용했습니다.
4.
초기 learning rate 로 0.256 을 설정했고 2.4 epoch 마다 0.97 배만큼으로 감소시켰습니다.
5.
SiLU(Swish-1) activation function 을 사용했습니다. ReLU 를 대체할 activation function 으로 제안된 것으로 ReLU 의 결과에 입력을 한 번 더 곱한 형태입니다. 2차원 feature map 을 확인할 때 ReLU 보다 더 부드러운 형태를 가지는 것으로 알려져 있습니다. 수식으로 표현하면 f(x)=x1+e−x=x⋅σ(x)f(x)=\frac{x}{1+e^{-x}}=x\cdot\sigma(x) 로 나타낼 수 있습니다.
6.
Cubuk et al. 에서 제시한 AutoAugment 를 사용해 최적의 augmentation 기법을 찾아냈습니다.
7.
Huang et al. 에서 제시한 Stochastic depth 를 사용해 residual module 을 0.2 의 확률로 drop 시켰습니다. 이는 dropout 과 비슷한 효과를 가진다고 합니다.
8.
큰 네트워크가 더 큰 regularization 이 필요함에 따라, EfficientNet-B0 에서 0.2 를 가졌던 dropout ratio 가 EfficientNet-B7 에서 0.5 를 가지도록 설계했습니다.
9.
Training dataset 에서 25K 의 이미지를 먼저 임의로 선택하여 Minival dataset 으로 명시하고, 이 Minival dataset 에 대해서 early stopping(epoch 마다 validation error 를 측정하고 validation error 가 증가하는 시점에서 미리 학습 중지) 을 구현했습니다. Validation set 의 accuracy 는 early stopped checkpoint 에서 평가하게 됩니다.
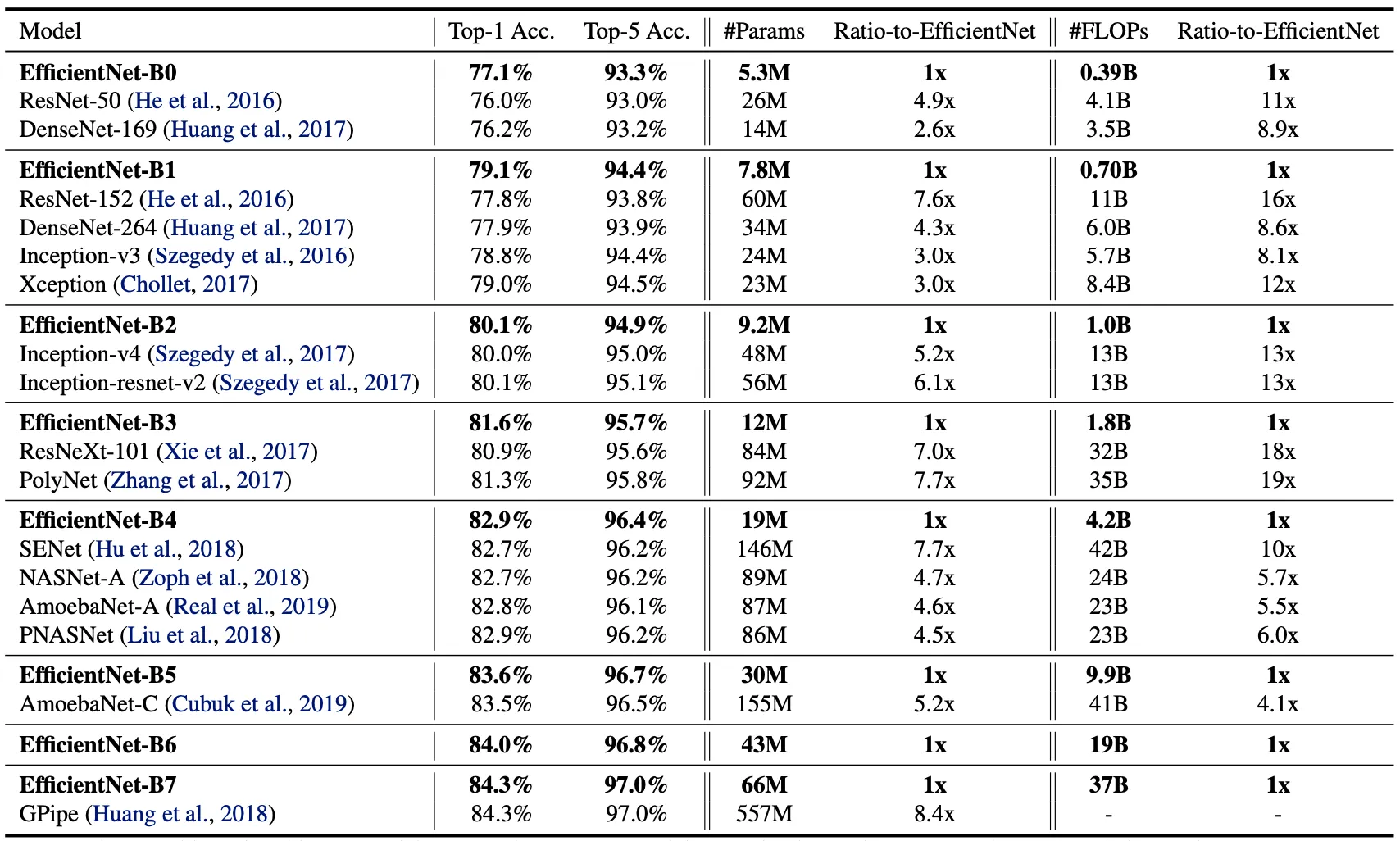
위의 구성을 사용해 학습을 진행한 결과는 아래의 표의 내용과 같습니다.
전체적으로 비슷한 성능을 내는 Convolutional Neural Network 에 비해서 논문의 EfficientNet 들이 더 적은 parameter 수와 FLOPs 를 가짐을 볼 수 있습니다. 특히 EfficientNet-B7 의 경우에는 66M 의 parameter 와 37B 의 FLOPs 를 가지고 top-1 accuracy 를 84.3% 를 달성했는데, 이는 기존에 존재하던 가장 좋은 네트워크인 GPipe 보다 더 정확한데 비해서 크기는 8.4 배 작습니다. 이러한 결과는 기존보다 더 좋은 baseline architecture, scaling method, 그리고 training settings 에 기반한 것으로 보고 있습니다.
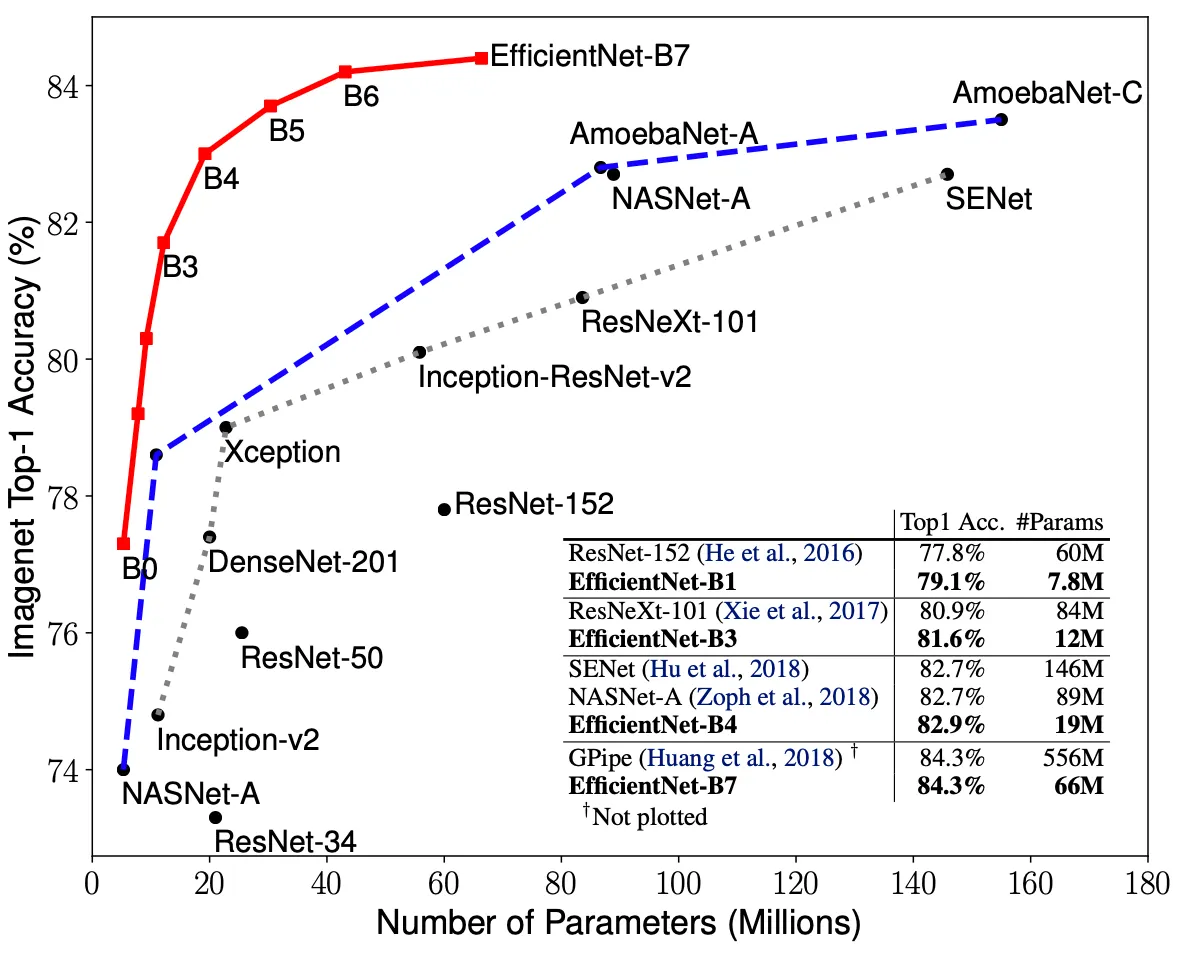
위 그림은 각각 EfficientNet 과 다른 Convolutional Neural Network 들을 Parameters-Accuracy 와 FLOPS-Accuracy 그래프 위에 나타낸 것입니다. 위의 표에서 살펴보았던 것과 같이 EfficientNet 이 다른 네트워크들에 비해서 더 적은 parameter 나 FLOPS 임에도 더 높은 accuracy 를 가짐을 시각적으로 볼 수 있습니다. 이는 단순히 네트워크가 작은 것 뿐만이 아니라 연산 자체가 비싸지 않다는 것까지 포함하는 결과입니다.
위의 결과가 실제로 inference latency 의 감소를 가져오는지를 검증하기 위해 논문에서는 EfficientNet 의 실제 latency 를 측정하여 그것과 Accuracy 가 비슷한 네트워크의 실제 latency 와 비교하는 작업을 진행합니다. 그 결과는 다음과 같습니다.
EfficientNet-B1 과 ResNet-152 는 accuracy 가 비슷한 두 네트워크인 반면 Latency 는 5.7 배 가량 EfficientNet 이 빠른 것으로 나타났습니다. 더불어 EfficientNet-B7 은 accuracy 가 비슷한 네트워크인 GPipe 에 비해서 6.1 배 가량 빠른 것으로 나타났습니다. 이러한 결과는 EfficientNet 가 실제 하드웨어 상에서도 빠르다는 것을 보여주는 결과로 해석할 수 있습니다.

Transfer Learning Results for EfficientNet

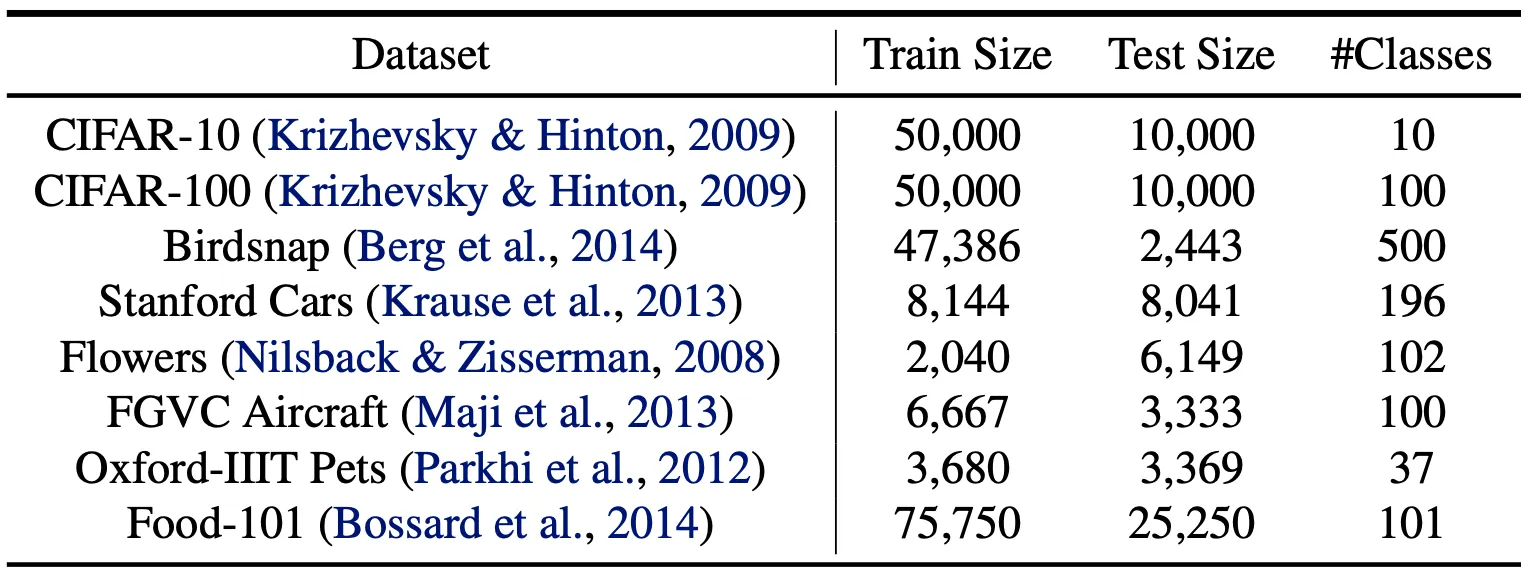
논문에서는 ImageNet 에서 벗어나 일반적으로 transfer learning 에 쓰이는 dataset 으로도 평가를 진행했습니다. 사용한 dataset 들의 정보는 아래의 표에 열거되어 있습니다.
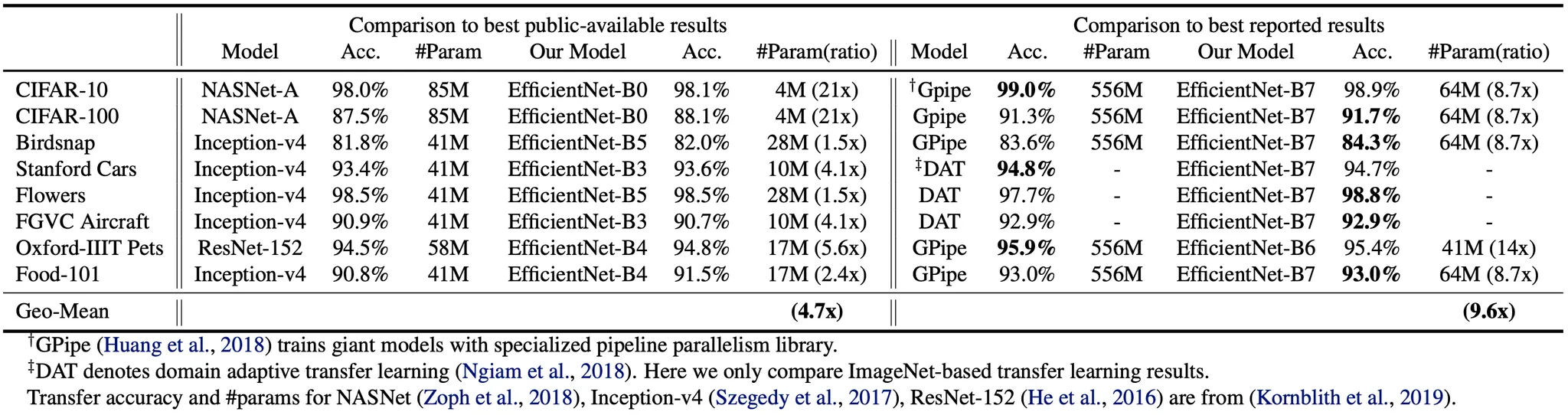
위 표의 구성으로 진행한 transfer learning performance 는 아래의 표에 나타납니다.
NASNet-A 와 Inception-v4 와 같은 public available model 과의 비슷한 accuracy 를 낸 EfficientNet 의 parameter 수를 각각 비교하면 EfficientNet 이 평균적으로 4.7 배 정도 적은 paramter 를 사용했고, 최대 21 배 적은 경우도 존재했습니다.
자체적으로 training data 를 동적으로 생성해내는 DAT 와 특별한 병렬 pipeline 을 활용하는 GPipe 등 SOTA model 과의 비슷한 accuracy 를 낸 EfficientNet 를 비교해보면 여전히 8 개의 비교 중 5 개의 경우에 대해서 더 좋은 accuracy 를 가짐을 확인할 수 있었고, EfficientNet 이 대략 9.6 배 정도 적은 parameter 수를 가지고 있음을 확인할 수 있었습니다.
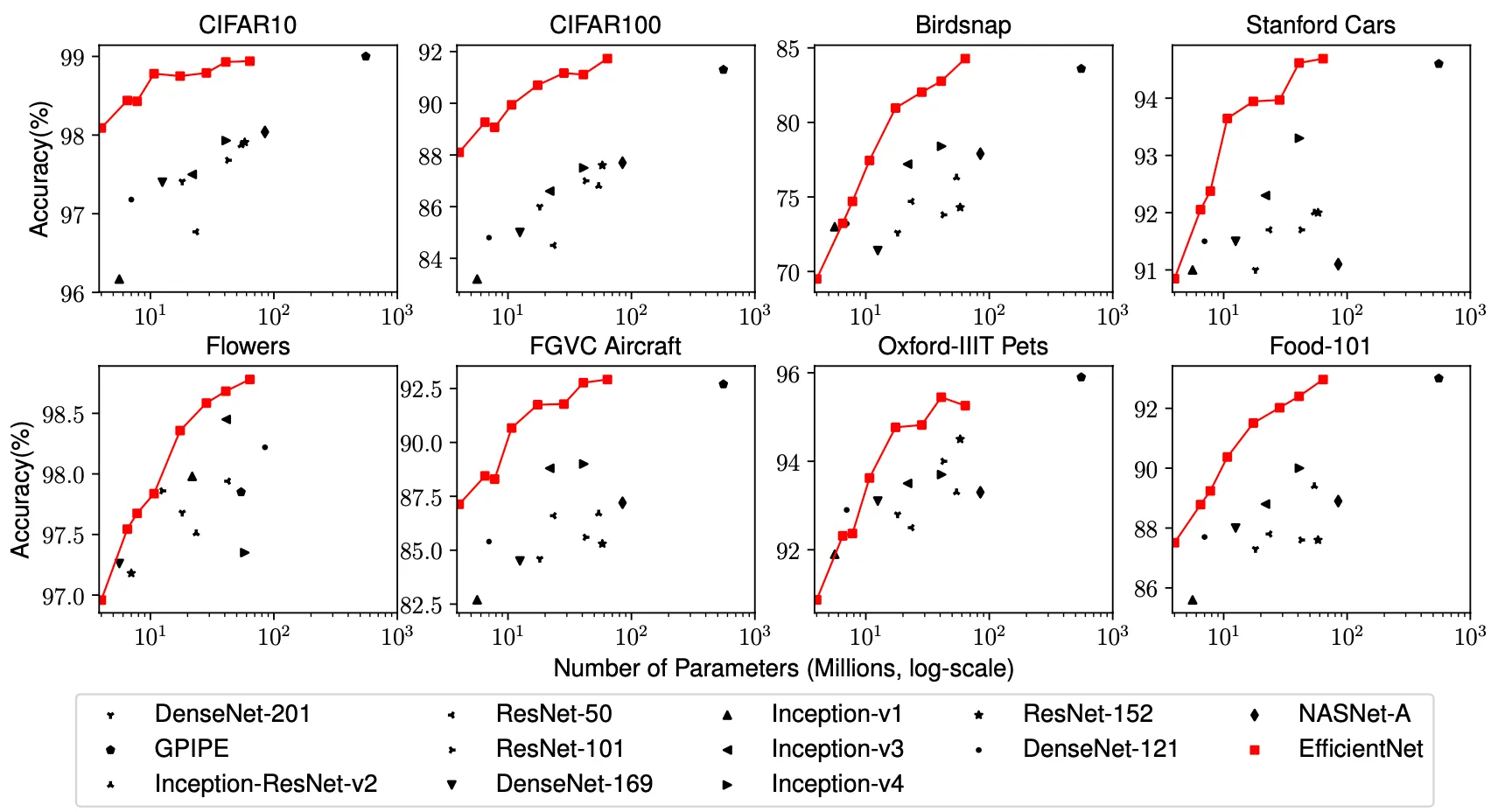
위의 그래프는 accuracy-parameter 의 그래프로 EfficientNet 이 일반적으로 다른 Convolutional Neural Network 에 비해서 적은 수의 parameter 를 가지고도 더 높은 accuracy 를 가짐을 시각적으로 알 수 있습니다.

Discussion

논문에서는 이어서 제시한 scaling method 가 얼마나 scaling methodology 측면에서 기여를 했는지를 보여주기 위해서 EfficientNet-B0 에서 서로 다른 scaling method 를 써서 나타난 accuracy 를 제시합니다.
위 그래프 & 표가 그 결과이며, 깊이, 너비, 그리고 이미지 크기를 사용한 single-dimension scaling 모두 compound scaling 과 비교하여 FLOPS 의 차이는 미비하지만 accuracy 측면에서 compound scaling 이 대략 2.5% 정도 우세한 것을 볼 수 있습니다.
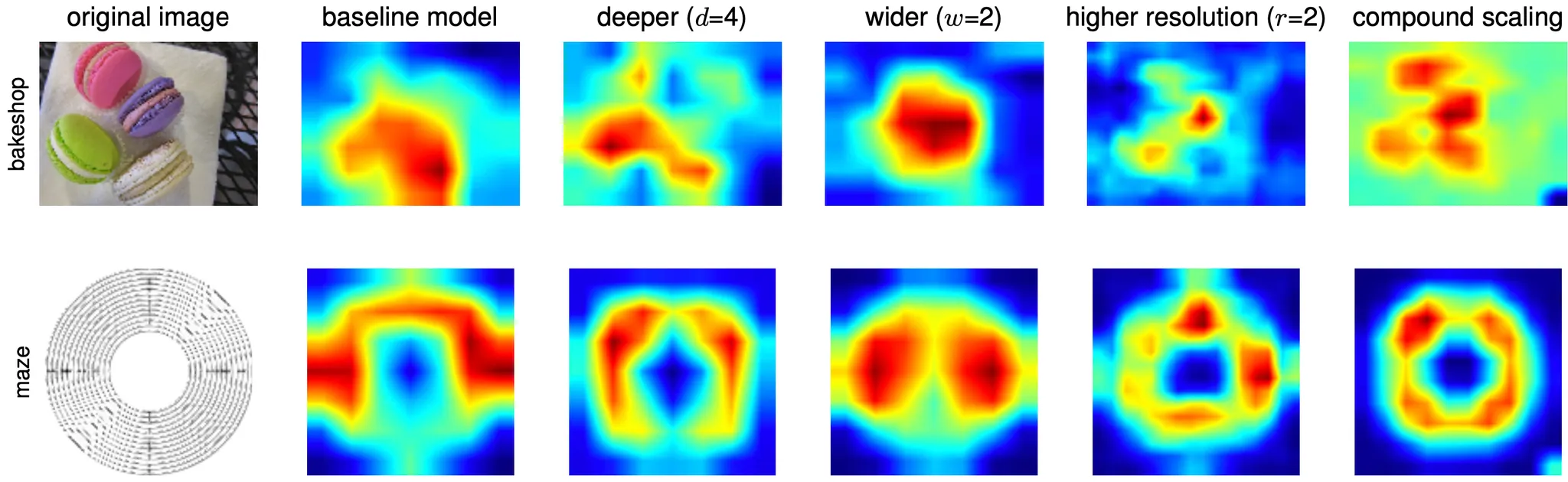
더불어 논문에서는 위의 5 가지 구성의 class activation map 의 그림을 제시하면서 compound scaling 이 이미지가 표현하는 물체의 관련 구역에 더 집중된 활성도를 가짐을 보여주었습니다. 그에 비해서 다른 single-dimension scaling 은 물체의 세부적인 디테일이 부족하거나 물체를 아예 인식하지 못하는 듯한 활성도를 보여주었습니다.

Conclusion

이것으로 논문 “EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks” 의 내용을 간단하게 요약해보았습니다.
컴퓨터 비전 관련 프로젝트를 진행할 때 baseline 으로 무엇을 사용하면 좋을까? 에 대한 질문에 EfficientNet 이 자주 등장하길래 눈여겨보고 있다가 이번 기회에 한 번 읽어보았습니다. 전반적으로 신박한 주제에 많은 사람들이 긍정적인 평가를 주고 있는 논문인 것 같은데 생각보다 이론적으로 잘 구성된 느낌은 아니었습니다. (특히 optimal 에 대한 증명이 없다는 부분이... 저는 그렇게 느껴졌습니다.) GoogLeNet 처럼 생각보다 논문을 설명하는데 기반이 되는 레퍼런스 논문들이 많지만, GoogLeNet 보다는 주요 내용을 이해하기에 편했던 것 같습니다. 더불어 SENet, MobileNet 등에 대한 제 관심도도 커진 것 같습니다.
이 논문도 Computer Vision 에 관심이 있으신 분들은 꼭 읽어보시는 것을 추천드립니다. 물론, 지금 읽기를 고민 중이시라면 MobileNet 을 먼저 읽는 것을 추천드리고 싶습니다.