Duplicate

Lecture 8 | Calibration

수강 일자
2023/02/26

Camera Calibration

•
Camera Projection Matrx P\rm P, 혹은 그것을 구성하는 요소인 K,R,tK,R, {\rm t} 를 얻는 방법임.
•
크게 DLT 와 Zhang’s Method, 두 가지 방법이 있음.

DLT

•
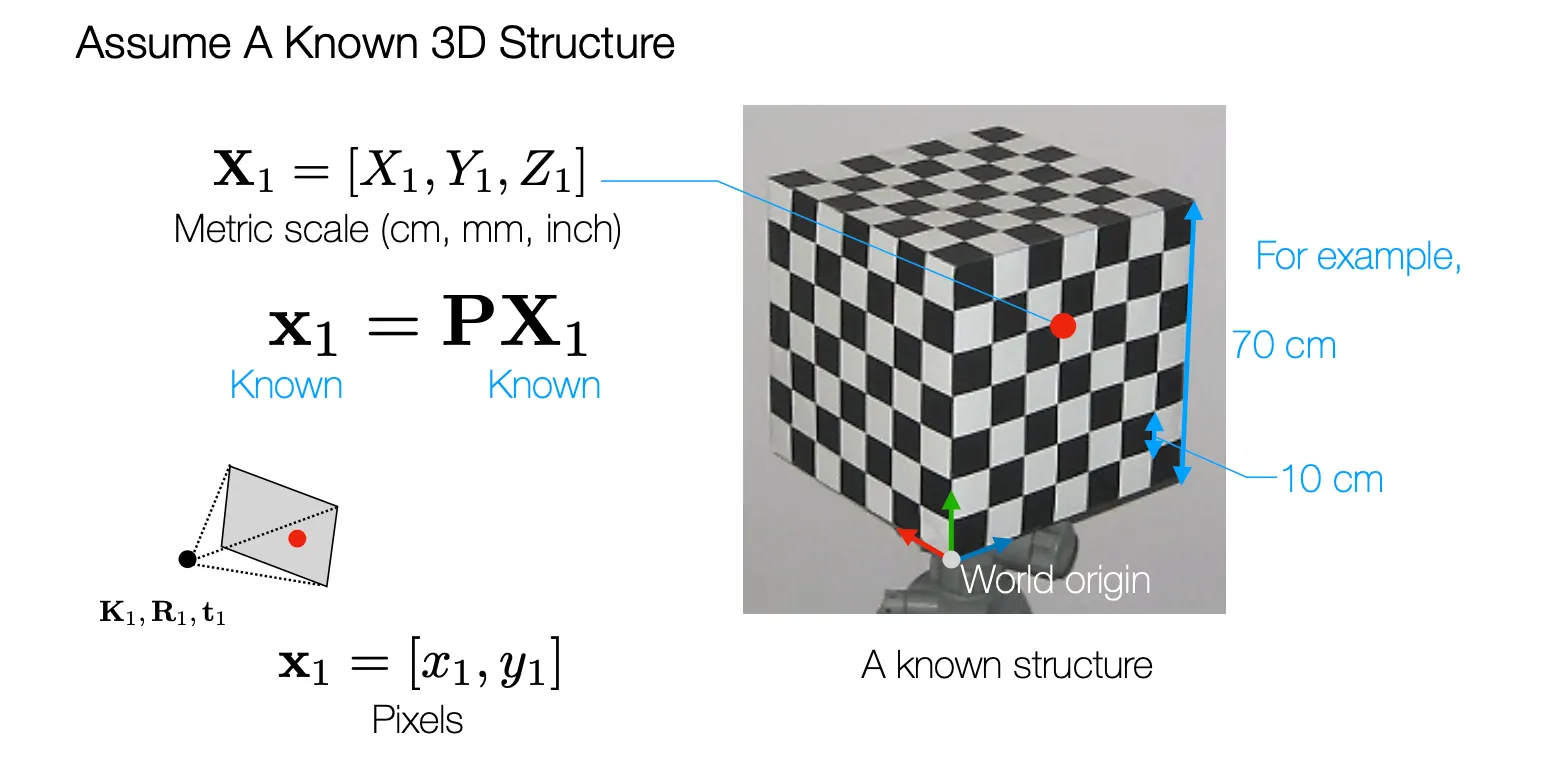
이미 알고 있는 3D Structure 에 기반한 방법임.
•
이미 알고 있는 3D Structure 이기 때문에 World Coordinate 에서의 위치 X1{\rm X_1} 와, 이미지에서의 위치 x1{\rm x_1}모두 알고 있음.
x1=PX1{\rm x_1} = {\rm PX_1}
•
P{\rm P} 를 구하기 위해 다음과 같이 DLT 방법론을 구성할 수 있음.
xi=[P11P12P13P14P21P22P23P24P31P32P33P34]Xixi=P11Xi+P12Yi+P13Zi+P14P31Xi+P32Yi+P33Zi+P34yi=P21Xi+P22Yi+P23Zi+P24P31Xi+P32Yi+P33Zi+P34{\rm x_i} = \begin{bmatrix} P_{11} & P_{12} & P_{13} & P_{14} \\ P_{21} & P_{22} & P_{23} & P_{24} \\ P_{31} & P_{32} & P_{33} & P_{34} \\ \end{bmatrix} {\rm X_i} \\ \quad \\ x_i = \frac{P_{11}X_i + P_{12}Y_i + P_{13}Z_i + P_{14}}{P_{31}X_i + P_{32}Y_i + P_{33}Z_i + P_{34}} \quad y_i = \frac{P_{21}X_i + P_{22}Y_i + P_{23}Z_i + P_{24}}{P_{31}X_i + P_{32}Y_i + P_{33}Z_i + P_{34}}
•
이는 Matrix Form 으로 나타내면 다음과 같음.
[XiYiZi1−xiXi−xiYi−xiZi−xiXiYiZi1−yiXi−yiYi−yiZi−yi][P11P12P13P14P21P22P23P24P31P32P33P34]=02×1\begin{bmatrix} X_i & Y_i & Z_i & 1 &&&&& -x_iX_i & -x_iY_i & -x_iZ_i & -x_i \\ &&&& X_i & Y_i & Z_i & 1 & -y_iX_i & -y_iY_i & -y_iZ_i & -y_i \end{bmatrix} \begin{bmatrix} P_{11} \\ P_{12} \\ P_{13} \\ P_{14} \\ P_{21} \\ P_{22} \\ P_{23} \\ P_{24} \\ P_{31} \\ P_{32} \\ P_{33} \\ P_{34} \\ \end{bmatrix} = 0_{2\times 1}
◦
11DoF System 이 구성되고 6 Corresponding Points 를 가지고 있으면 P{\rm P} 를 계산할 수 있음.

Summary: DLT for Computing P{\rm P}

•
P{\rm P} 계산에 DLT 를 사용하는 방법론의 프로세스는 다음과 같음.
◦
이미 알고 있는 3D Structure 를 준비함.
◦
이미지를 준비함.
◦
6 개의 Corresponding Points 를 찾음.
◦
DLT 문제를 풀어 최종적으로 P{\rm P} 를 계산함.
•
P{\rm P} 계산에 DLT 를 사용하는 방법론의 단점은 다음과 같음.
◦
이미 알고 있는 3D Structure 를 준비하는 것이 어려움. (
◦
Degenerate 한 경우가 존재함.
1.
모든 point 가 동일한 plane 에 있는 경우
2.
모든 point 가 quadric 위에 있는 경우

Decomposition of the Camera Matrix

P=K[R∣t]=K[R∣−RCworld]=[KR∣−KRCworld]{\rm P} = K[R | {\rm t}] = K[R| -R{\rm C_{world}}] = [KR | -KR{\rm C_{world}}]
•
PCworld=0{\rm PC_{world}} = 0 이므로, P{\rm P} 를 알고 있다면 P{\rm P} 의 Null Space 를 통해 Cworld{\rm C_{world}} 를 구할 수 있음.
•
K,RK, R 은 P{\rm P} 의 좌측 3×33\times 3 matrix 를 RQ Decomposition 을 하여 구해낼 수 있음.

Uniqueness of K and R (RQ Decomposition)

D=[±1000±10001]→P1:3=KR=KDDRD= \begin{bmatrix} \pm1 & 0 & 0 \\ 0 & \pm1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \\ \to {\rm P}_{1:3} = KR = KDDR
•
KDKD 는 Upper Triangle Matrix 가 됨.
•
DRDR 은 Rotation Matrix 가 됨.
◦
(DR)(DR)T=(DR)(RTDT)=DDT=I(DR)(DR)^T = (DR)(R^TD^T) = DD^T = I → Orthogonal !
◦
det(DR)=det(D)det(R)=1det(DR) = det(D)det(R) = 1
•
즉, RQ Decomposition 으로 구한 K,RK, R 에 적어도 4 개의 variation 이 존재하기 때문에 엄밀히 말하면 unique 하지는 않음.

Zhang’s Method

•
Camera Calibration 을 할 때 가장 일반적으로 사용되는 방법론임.
•
Zhang’s Method 의 프로세스는 다음과 같음.
1.
알려진 사이즈의, Checkerboard Pattern 판을 준비함.
2.
하나의 viewpoint 에서 해당 Checkerboard 를 캡처한 이미지를 준비함.
3.
캡처한 이미지에서 보이는 Checkerboard Plane 상의 축을 x,yx, y 로, 그것과 수직인 방향을 zz 로 설정하고, Camera System 식을 구성함.
[xy1]≡K[R∣t][XY01]→λ[xy1]=K[r1 r2 r3 t][XY01]→λ[xy1]=K[r1 r2 t][XY1]\begin{align*} &\begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \equiv K[R|{\rm t}] \begin{bmatrix} X \\ Y \\ 0 \\ 1 \end{bmatrix} \\ \to &\lambda \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = K [r_1\ r_2\ r_3\ {\rm t}]\begin{bmatrix} X \\ Y \\ 0 \\ 1 \end{bmatrix} \\ \to &\lambda \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = K [r_1\ r_2\ {\rm t}]\begin{bmatrix} X \\ Y \\ 1 \end{bmatrix} \\ \end{align*}
•
3D Coordinate 에서 Z=0Z =0 임을 알 수 있음.
•
r1,r2,r3r_1, r_2,r_3 는 RR 의 column vector 들임.
4.
4 개의 점을 뽑아서 식을 구성할 수 있기 때문에 Homography 를 구할 수 있음.
H=K[r1 r2 t]→λ[h1 h2 h3]=K[r1 r2 t]{\rm H} = K[r_1\ r_2\ {\rm t}] \to \lambda[{{\rm h}_1\ {\rm h}_2\ {\rm h}_3}] = K[r_1\ r_2\ {\rm t}]
이는 다음과 같이 적을 수 있음.
λK−1h1=r1λK−1h2=r2\lambda K^{-1}{\rm h_1} = r_1 \quad \lambda K^{-1}{\rm h_2} = r_2
5.
r1,r2r_1, r_2 는 rotation matrix 의 column 이므로 orthonormal 하기 때문에 다음이 성립함.
r1Tr2=0→h1TK−TK−1h2=0∥r1∥=∥r2∥=0→h1TK−TK−1h1=h2TK−TK−1h2=0r_1^T r_2 = 0\quad \to \quad {\rm h_1}^TK^{-T}K^{-1}{\rm h}_2 = 0 \\ \|r_1\| = \|r_2\| = 0 \quad \to \quad {\rm h_1}^TK^{-T}K^{-1}{\rm h}_1 = {\rm h_2}^TK^{-T}K^{-1}{\rm h}_2 =0
이 때 B=K−TK−1{\rm B} = K^{-T}K^{-1} 로 지정할 수 있음.
6.
이렇게 구한 B\rm B 에 대해서 다시 또 DLT 를 사용할 수 있음.
BT=B→DoF=6B^T=B \to {\rm DoF} = 6
앞선 식 h1TK−TK−1h2=0{\rm h_1}^TK^{-T}K^{-1}{\rm h}_2 = 0, h1TK−TK−1h1=h2TK−TK−1h2=0{\rm h_1}^TK^{-T}K^{-1}{\rm h}_1 = {\rm h_2}^TK^{-T}K^{-1}{\rm h}_2 =0 로 두 개의 식을 구성할 수 있고 (왜 3 개가 아닐까…?), 총 3 개의 이미지를 통해 다른 Homography 를 구해낸다면, B\rm B 를 구할 수 있음.
7.
B\rm B 를 구하면, Cholesky Decomposition 을 통해 KK 를 구할 수 있음.
8.
KK 를 구하면, Extrinsic Parameters 인 RR 의 각 요소 r1,r2,r3r_1, r_2, r_3 는 다음과 같이 구할 수 있음.
λK−1h1=r1λK−1h2=r2→r1=K−1h1∥K−1h1∥r2=K−1h2∥K−1h2∥r3=r1×r2\lambda K^{-1}{\rm h}_1 = r_1 \quad \lambda K^{-1}{\rm h}_2 = r_2 \\ \to r_1 = \frac{K^{-1}{\rm h}_1}{\|K^{-1}{\rm h}_1\|} \quad r_2 = \frac{K^{-1}{\rm h}_2}{\|K^{-1}{\rm h}_2\|} \quad r_3 = r_1 \times r_2
9.
t{\rm t} 는 다음과 같이 구할 수 있음.
t=K−1h3λ=K−1h3∥K−1h1∥{\rm t} = \frac{K^{-1}{\rm h}_3}{\lambda} = \frac{K^{-1}{\rm h}_3}{\|K^{-1}{\rm h}_1\|}

The Image of the Absolute Conic

B=K−TK−1{\rm B}=K^{-T}K^{-1}
•
사실 앞선 Zhang’s Method 에서 사용한 B\rm B 는 Absolute Conic 의 이미지와 동일함.
•
구체적으로 다루지는 않음.

Lens Distortion

•
이미지 중심으로부터 멀 수록 Lens Distortion 이 심한 것을 알 수 있음.
•
Lens Distortion 을 없애는 과정이 필요함.
◦
Straight Line 은 이미지로 보았을 때도 Straight Line 이어야 함.

Lens Distortion Model

[xdistydist]=(1+k1r2+k2r4+k3r6)[xy]+[2p1xy+p2(r2+2x2)p1(r2+2y2)+2p2xy]\begin{bmatrix} x_{\rm dist} \\ y_{\rm dist} \end{bmatrix} = (1 +k_1r^2 +k_2r^4 + k_3r^6) \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} 2p_1xy+p_2(r^2 + 2x^2) \\ p_1(r^2 + 2y^2) + 2p_2xy \end{bmatrix}
•
Distortion Parameters: k1,k2,k3,p1,p2k_1, k_2, k_3, p_1,p_2
•
rr 은 Camera Center (이미지 중심) 으로부터의 거리를 의미함.
•
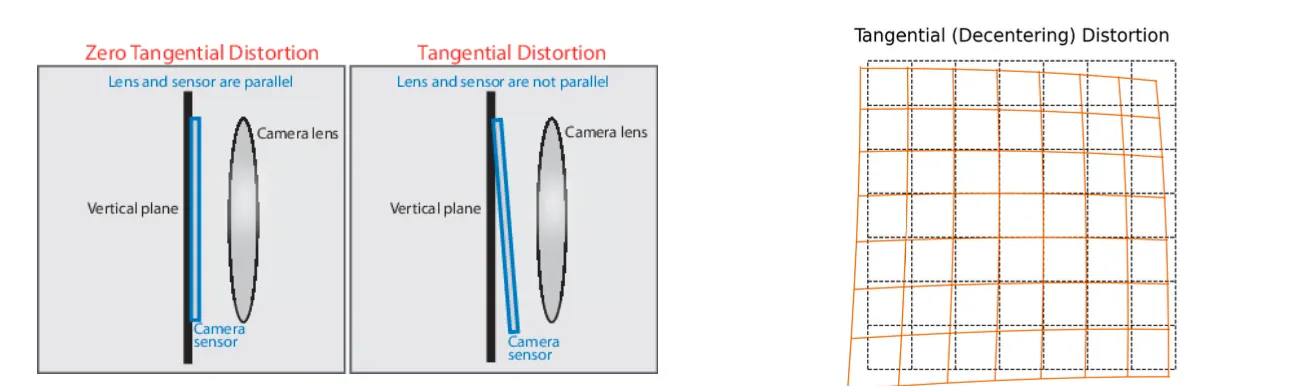
앞 부분 항목을 Radial Distortion, 뒷 부분 항목을 Tangential Distortion 이라고 함.
◦
보통 Tangential Distortion 은 무시할 수 있어 앞 부분만을 다룸.
•
일반적으로 k>0k>0 이면 distorted pixel 값이 기존보다 커지기 때문에 Positive Radial Distortion 이 나타나고 k<0k <0 이면 distorted pixel 값이 기존보다 작아지기 때문에 Negative Radial Distortion 이 나타남.
•
Radial Distortion 을 없애기 위해서 사용할 원본의 coordinate 는 Intrinsic Parameter 를 제거하고 (remove 2D projection, change to principle point offset) normalize 를 해야함.
[xcyczc]=K−1[xpyp1]x=xczcy=yczcr2=x2+y2\begin{bmatrix} x_c \\ y_c \\ z_c \end{bmatrix} = K^{-1} \begin{bmatrix} x_p \\ y_p \\ 1 \end{bmatrix} \\ x = \frac{x_c}{z_c} \quad y = \frac{y_c}{z_c} \quad r^2 = x^2 + y^2
•
Tangential Distortion 은 Lens 와 Image Plane 과 평행을 이루지 않는 경우에 한해서 나타나는 특이한 distortion 인데, 현대의 camera 에서는 많이 발생하지는 않음.
•
이러한 모델이 어떻게 유도되었는지는 구체적으로 다루지 않음. (Optics Course 를 수강하기를…)

Removing Lens Distortion

•
Original Image 로부터 Ideal Image 를 만들고 싶은 경우 Target (Ideal Image) 의 pixel 위치에서부터 시작하여 해당 픽셀과 대응되는 Original Image 의 픽셀 값을 찾고 (일반적으로 floating point) 그 값을 Bilinear Interpolation 을 통해서 계산해 가져와 만듬.
•
일반적으로 Homography 를 적용할 때도 마찬가지로 Target → Source 방향으로 값을 가져옴.