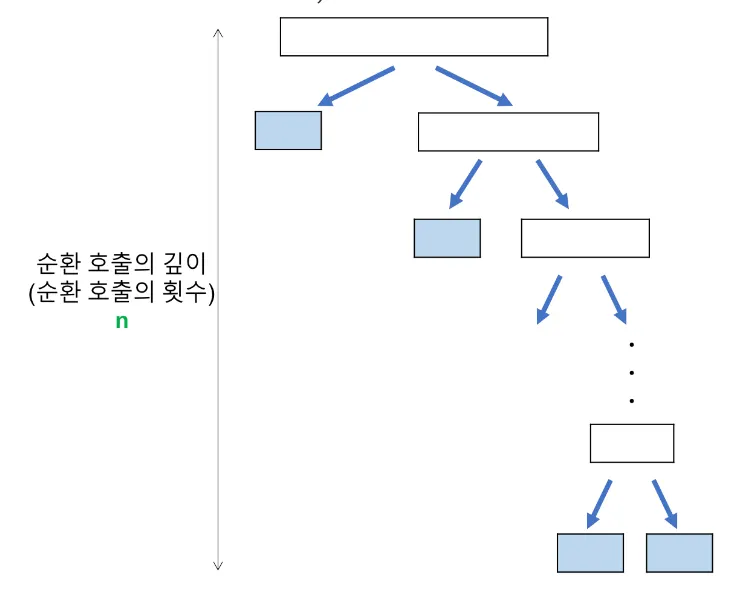
Sorting Methods
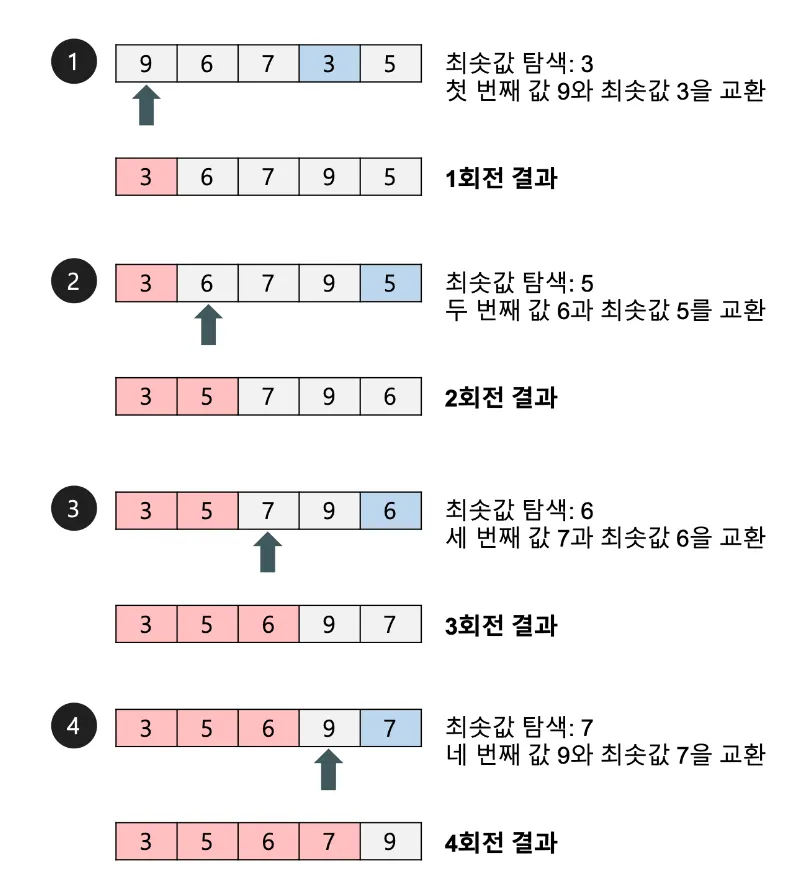
Selection Sort
1.
전체를 순회하여 최솟값을 찾아 처음에 둠
2.
첫 값을 제외하고 반복, 1 ~ 2 값을 제외하고 반복 …
시간 복잡도:
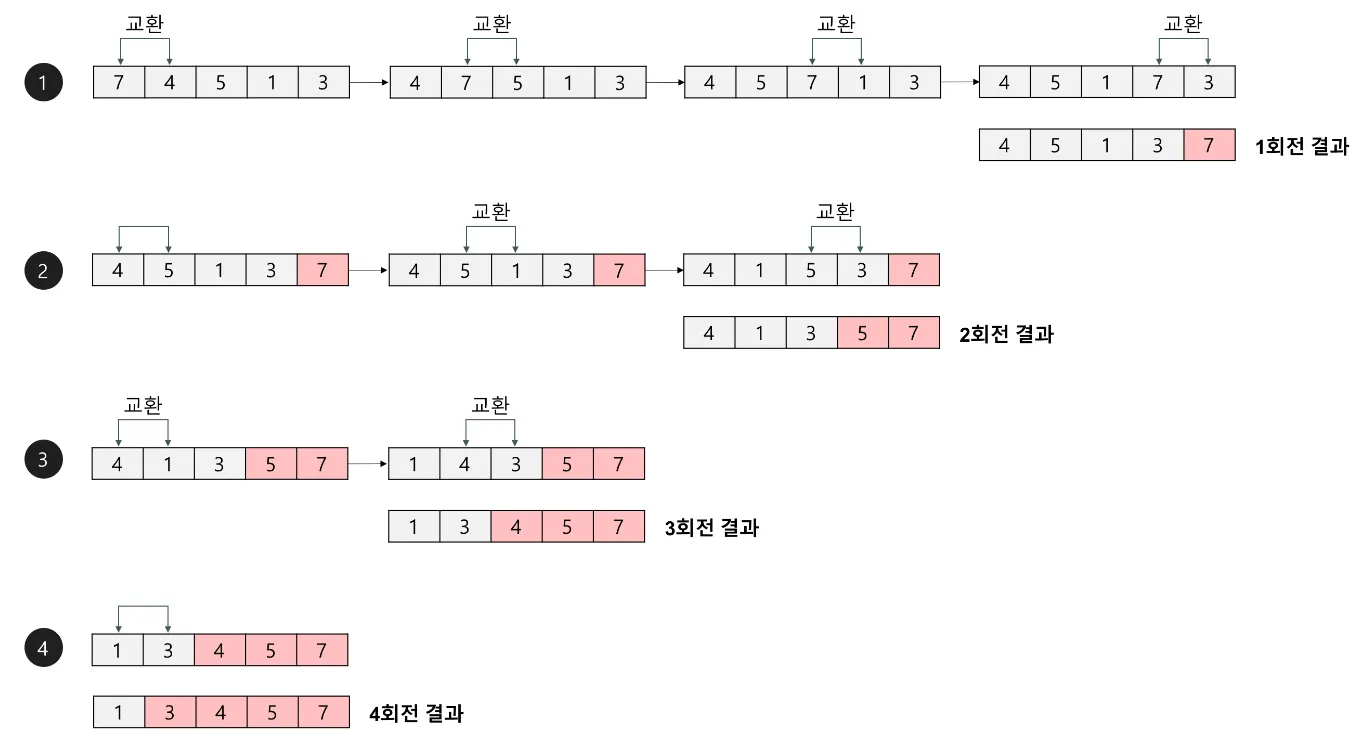
Bubble Sort
1.
1항과 2항을 비교해 1항이 2항보다 작으면 교체
2.
2항과 3항, 3항과 4항 … 을 반복하여 제일 끝에 결국 마지막 항이 가장 크게 변화함
3.
마지막 항을 제외하고 반복, 마지막 두 항을 제외하고 반복 …
시간 복잡도:
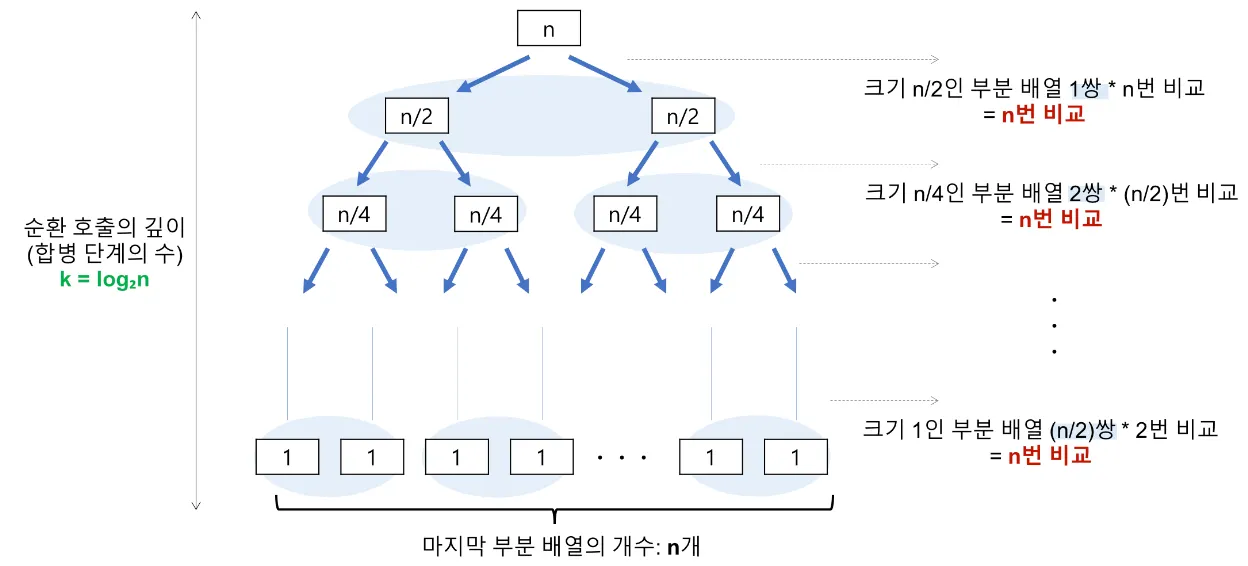
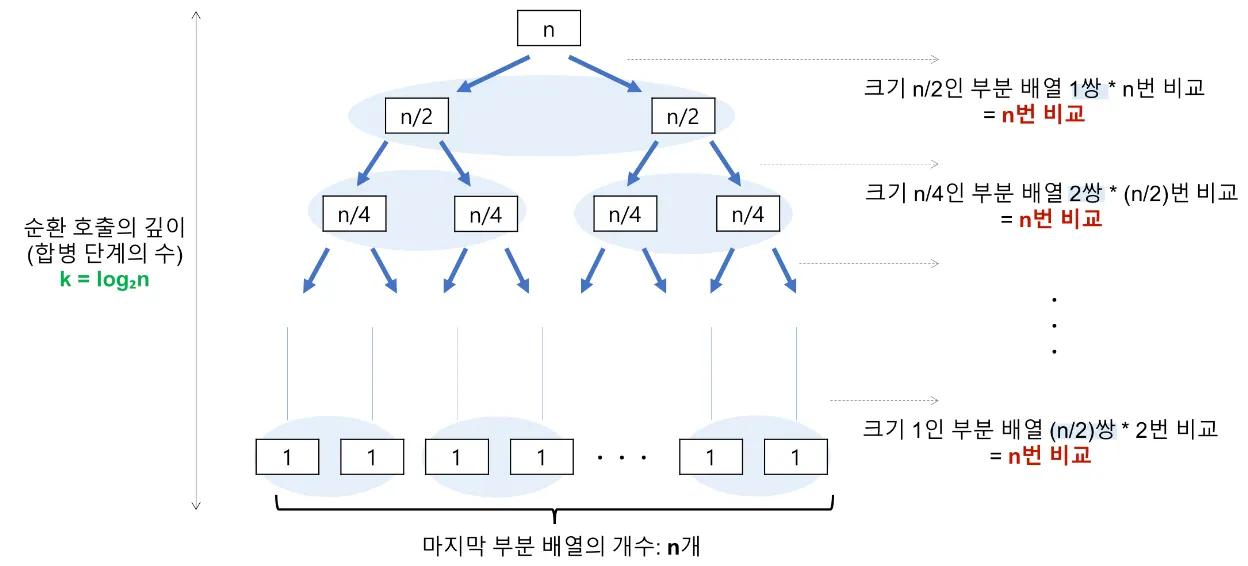
Merge Sort
1.
리스트를 절반의 길이를 가지는 두 개의 리스트로 쪼갠다 (Divide)
2.
쪼갠 리스트 각각을 정렬한다 (Conquer) → 길이가 절반인 동일한 문제를 해결
3.
정렬된 각각의 리스트의 앞 값끼리 비교해나가며 새로운 리스트를 완성한다 (Combine)
시간 복잡도:
Quick Sort
1.
Pivot 을 정하고 남은 리스트 양 끝점에서 인덱스를 지정
2.
좌측 인덱스는 pivot 보다 큰 값이 올 때까지 이동하고, 우측 인덱스는 pivot 보다 작은 값이 올 때까지 이동하여 둘을 교체하는 과정을 반복
3.
두 인덱스가 교차할 때 좌측 인덱스를 pivot 과 교체
4.
pivot 을 기준으로 좌측은 pivot 보다 작은 값들이, 우측은 pivot 보다 큰 값들이 모이게 되고 pivot 기준으로 나누어진 두 리스트를 다시 recursive 하게 정렬
평균 시간 복잡도:
Worst Case
Reference: https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html
최강 시간 복잡도:
Binary Search
정렬된 자료 구조에서 원하는 값을 찾는 방법
1.
절반의 위치의 값과 비교해서 찾으려는 것이 그것보다 크면 우측에서, 찾으려는 것이 그것보다 작으면 좌측에서 찾음.
2.
1을 반복
시간 복잡도:
Binary Tree Traversal
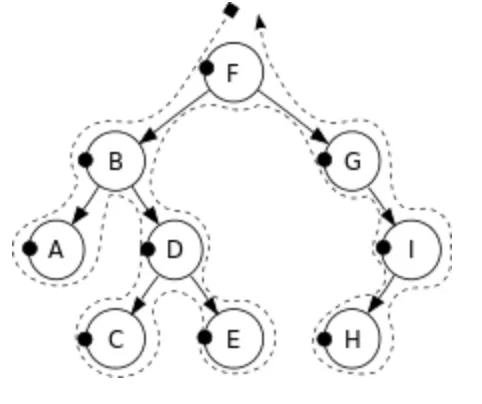
Preorder Traversal
모든 분기점에서 중 → 왼 → 오 순서로 traversal
노드를 처음에 방문에서 Preorder Traversal 이라고 명칭
F → B → A → D → C → E → G → I → H
void traversal(node){
if(node){
visit(node); // inorder
traversal(node->left);
traversal(node->right);
}
}
Shell
복사
DFS 의 좌측 기준 버전 느낌으로 해석 가능
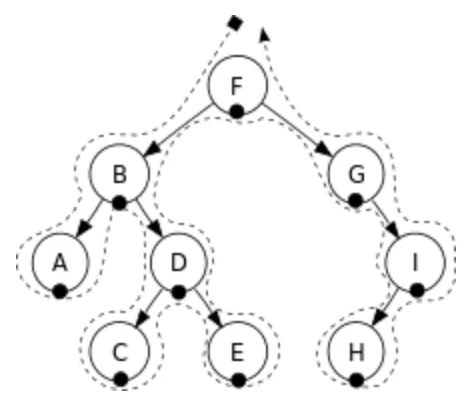
Inorder Traversal
모든 분기점에서 왼 → 중 → 오 순서로 traversal
노드를 중간에 방문해서 Inorder Traversal 이라고 명칭
A → B → C → D → E → F → G → H → I
void traversal(node){
if(node){
traversal(node->left);
visit(node); // inorder
traversal(node->right);
}
}
Shell
복사
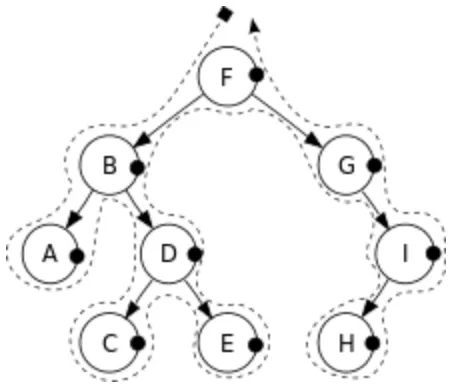
Postorder Traversal
모든 분기점에서 왼 → 오 → 중 순서로 traversal
노드를 끝에 방문해서 Postorder Traversal 이라고 명칭
A → C → E → D → B → H → I → G → F
void traversal(node){
if(node){
traversal(node->left);
traversal(node->right);
visit(node); //postorder
}
}
Shell
복사
Binary Search Tree
Find → Preorder Traversal:
Insert → Always on Leaf Node:
Delete
•
자식 노드가 없다면? → 그냥 삭제
•
자식 노드가 하나라면? → 그냥 부모랑 이어버림
•
자식 노드가 두 개라면? → Predecessor 와 Successor 중 하나를 그 위치로 끌고 옴
◦
Predecessor 는 좌측 트리 중 가장 큰 값
◦
Successor 는 우측 트리 중 가장 작은 값
◦
Inorder Traversal 시에 오름차순이 되어야 하기 때문에 이 두 값을 끌어올리는 것이고, 이 둘은 항상 자식 노드가 하나 또는 없기 때문에 그냥 삭제하거나 부모랑 이어버릴 수 있음
•
찾아서 지워야 하기 때문에
다만 위 은 균형이 잡힌 AVL Tree 에서만 성립하는 이야기이며 균형이 망가지면 트리의 높이가 달라져 까지 가능함
AVL Tree
Balance Factor (BF): 좌측 트리의 높이 - 우측 트리의 높이
BF 의 절댓값이 2이하가 될 때 이를 조정하여 1 이하로 만들어주기 위해 Tree Rotation 을 진행
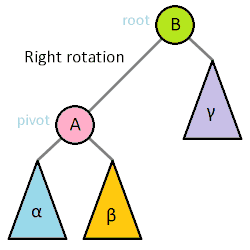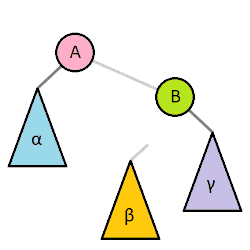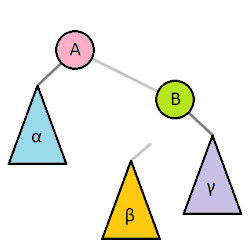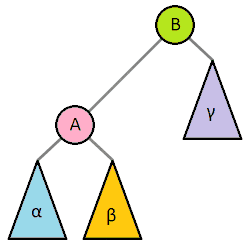
Right Rotation: 좌측 자식의 우측 트리를 본인의 좌측 트리로 만들어버리고, 좌측 자식을 루트로, 본인은 바뀐 루트의 우측 트리 루트가 되어버림
Left Rotation: 우측 자식의 좌측 트리를 본인의 우측 트리로 만들어버리고, 우측 자식을 루트로, 본인은 바뀐 루트의 좌측 트리 루트가 되어버림
Double Rotation (LR): 좌측 트리의 BF 가 -1 본인은 2 일 때 좌측 트리를 Left Rotation 후 다시 바뀐 트리에서 좌측 트리를 Right Rotation
Double Rotation (RL): 우측 트리의 BF 가 1 본인은 -2 일 때 우측 트리를 Right Rotation 후 다시 바뀐 트리에서 우측 트리를 Left Rotation
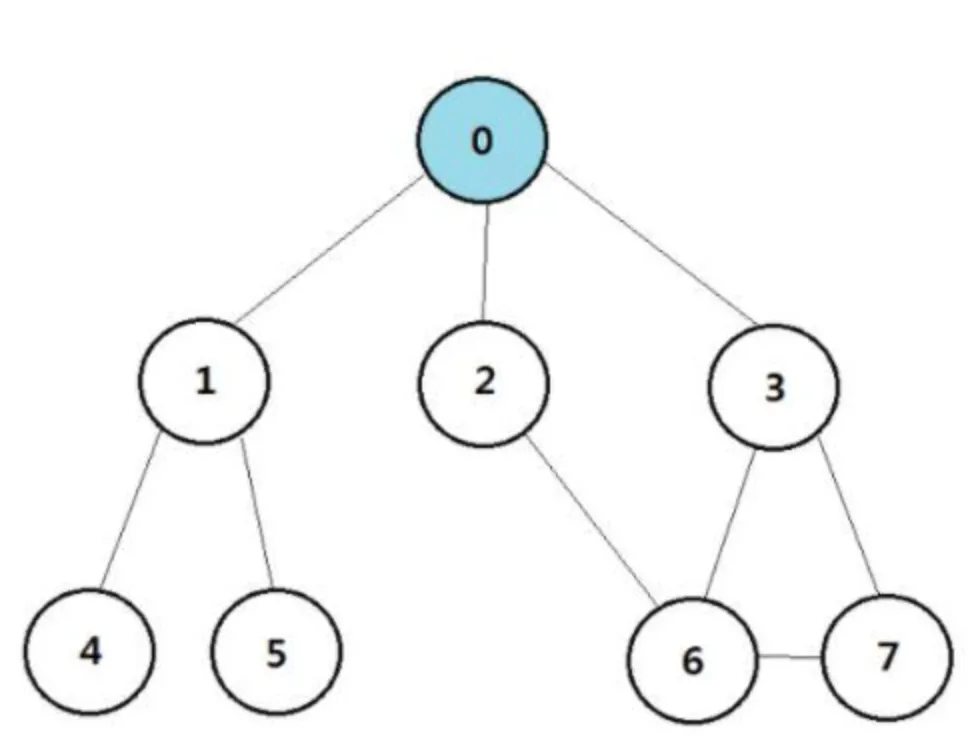
DFS
Graph Traversal 방법 중 하나. Preorder Traversal 과 방법이 유사
구현에는 순환호출을 사용할 수도, Stack 을 사용할 수도 있음
Reference:
https://sorjfkrh5078.tistory.com/26
Stack 사용 시
→ 처음에 시작 노드를 넣고 매 번 스택에서 하나를 꺼내 방문하지 않은 주변 노드를 모두 넣는 것을 반복
→ 스택에 넣는 순간에 방문처리를 함
Stack
0 → 3, 2, 1 → 3, 2, 4, 5 → 3, 2, 4 → 3, 2 → 3, 6 → 3, 7 → 3 → End
void search(Node root) {
if (root == null) return;
// 1. root 노드 방문
visit(root);
root.visited = true; // 1-1. 방문한 노드를 표시
// 2. root 노드와 인접한 정점을 모두 방문
for each (Node n in root.adjacent) {
if (n.visited == false) { // 4. 방문하지 않은 정점을 찾는다.
search(n); // 3. root 노드와 인접한 정점 정점을 시작 정점으로 DFS를 시작
}
}
}
Shell
복사
Reference: https://gmlwjd9405.github.io/2018/08/14/algorithm-dfs.html
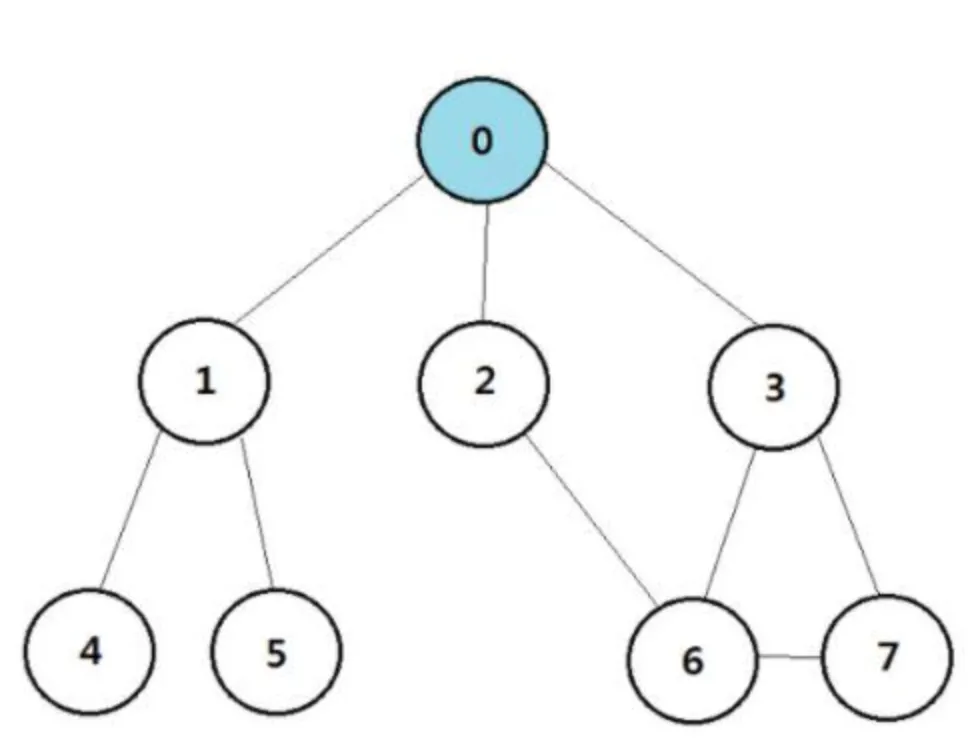
BFS
Graph Traversal 방법 중 하나. 거리가 짧은 지점부터 탐색하는 방법
구현에는 Queue 를 사용
Reference:
https://sorjfkrh5078.tistory.com/26
Queue 사용 시
→ 처음에 시작 노드를 넣고 매 번 큐에서 하나를 꺼내 방문하지 않은 주변 노드를 모두 넣는 것을 반복
→ 큐에 넣는 순간에 방문처리를 함
Queue
0 → 1, 2, 3 → 2, 3, 4, 5 → 3, 4, 5, 6 → 4, 5, 6, 7 → 5, 6, 7 → 6, 7 → 7 → End
void search(Node root) {
Queue queue = new Queue();
root.marked = true; // (방문한 노드 체크)
queue.enqueue(root); // 1-1. 큐의 끝에 추가
// 3. 큐가 소진될 때까지 계속한다.
while (!queue.isEmpty()) {
Node r = queue.dequeue(); // 큐의 앞에서 노드 추출
visit(r); // 2-1. 큐에서 추출한 노드 방문
// 2-2. 큐에서 꺼낸 노드와 인접한 노드들을 모두 차례로 방문한다.
foreach (Node n in r.adjacent) {
if (n.marked == false) {
n.marked = true; // (방문한 노드 체크)
queue.enqueue(n); // 2-3. 큐의 끝에 추가
}
}
}
}
Shell
복사
Reference: https://gmlwjd9405.github.io/2018/08/15/algorithm-bfs.html
Dijkstra Algorithm
특정 노드로부터 다른 모든 노드로 갈 수 있는 최소 거리를 구하는 알고리즘
아직 방문하지 않은 노드 중 가장 거리가 가까운 노드를 다음 방문 노드로 선택하여 거리를 갱신하는 과정을 반복하는 알고리즘
순차 탐색 시 →
우선순위 큐 활용 시 →
Minimum Spanning Tree
Spanning Tree: 모든 노드를 연결하는, 최소 연결 부분 트리 (간선의 수가 가장 적은 연결 트리)
Minimum Spanning Tree: Spanning Tree 들 중에서 간선들의 가중치 합이 최소인 트리
Kruskal MST Algorithm
1.
모든 간선들의 가중치를 오름차순으로 정렬한 뒤, 작은 것 부터 선택
2.
선택할 간선을 추가했을 때 루프가 만들어진다면 생략하고 다음 것을 선택
간설들의 가중치를 정렬하는 시간 복잡도 →
루프 검증에 Union-Find 를 사용할 경우 위의 시간 복잡도가 최종 시간 복잡도
Prim MST Algorithm
1.
시작 노드를 MST 에 포함
2.
현재 MST 에서 MST 가 아닌 점들과 연결되는 인접 간선들 중 최소 가중치 간선을 더해 그 노드를 MST 에 포함시키는 과정을 반복
포함시키는 과정을 총 노드의 수만큼 반복해야 하고, 각 과정마다 노드를 순회하며 연결된 것들 중 최소를 찾아야 해서
적은 간선일 시 Kruskal, 간선이 많으면 Prim 이 적합함!
1. Devide & conquer
- binary search
- merge sort
- Quick sort
- Strassen's Matrix Multiplication
2.Dyramic programming
- Binomial coefficient
- Floydis algorithm
- Optimization problem
- TSP
3.The Greedy Approach
- MST
- Dijkstra's
- Scheduling
- Huffmun Code
- Knapsack problem
4.Back Tracking
- n-Queen Problem
- Monte Carlo
- Cdoriny numitonian ciruit
Plain Text
복사