Duplicate

Lecture 17 | Radiometry / Photometric Stereo

수강 일자
2023/03/05

Understanding Image Intensity

•
3D information 과 Intensity, Lighting, Normal 의 관계가 무엇일까?
◦
Shape from Shading
▪
Input: An Image
▪
Output: Suface Normals
◦
Photometric Stereo
▪
Input: Multiple Images with different Light Conditions
▪
Output: Surface Normals → 이미지와 그 픽셀 색상으로 normal 을 표현할 수 있음.

How Image Intensity is Determined

Image Intensity=f(Illumination, Surface Orientation, Surface Reflectance){\rm Image\ Intensity} ={\rm f}(\rm Illumination,\ Surface\ Orientation,\ Surface\ Reflectance)
•
Image Intensity (pixel value) 로부터 Surface Orientation (Normal Direction) 이 목표임.
•
Surface Orientation 을 얻으면 3D Shape 을 계산할 수 있음.

3D Polar Angle

•
Zenith: 법선으로부터 Ray 와의 각도
•
Azimuth: 평면 위의 고정된 north 에서부터 ray 의 projection 위치까지의 각도

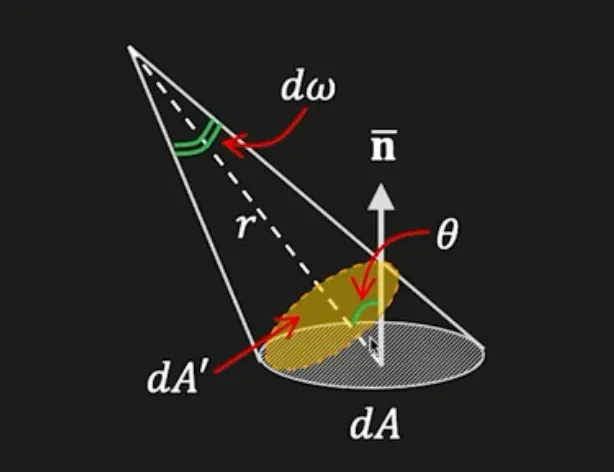
Concept: Angle (2D) & Solid Angle (3D)

dθ=dlrdω=dA′r2=dAcos⁡θr2d\theta = \frac{dl}{r}\quad d\omega = \frac{dA'}{r^2}=\frac{dA\cos\theta}{r^2}
•
Angle
◦
Radian 각은 반지름과 호의 비율로 정의할 수 있음.
◦
원은 2π2\pi radian 을 가짐.
•
Solid Angle
◦
Steradian 각은 평면과의 거리와 사영된 면적으로 정의할 수 있음.
◦
High AA, High Solid Angle ω\omega
◦
Low rr, High Solid Angle ω\omega
◦
Low θ\theta, High Solid Angle ω\omega
◦
Sphere 는 4π4\pi steradian 을 가짐.

Concept: Light Flux & Surface Irradiance / Radiance

dΦE=dΦdAL=d2Φ(dAcos⁡θγ)dωd\Phi\quad E=\frac{d\Phi}{dA}\quad L = \frac{d^2\Phi}{(dA\cos\theta_{\gamma})d\omega}
•
Light Flux (Φ\Phi)
◦
Solid Angle 을 통해 방출되는 Power (단위: WW)
•
Surface Irradiance (EE)
◦
단위 면적 당 받는 Light Flux (단위: W/m2W/m^2)
◦
JJ 가 단위 Solid Angle 당 Flux 이면, Light Flux Φ=Jdω\Phi = Jd\omega
E=dΦdA=JdωdA=JdAcos⁡θr2dA=Jcos⁡θr2E=\frac{d\Phi}{dA}=\frac{Jd{\omega}}{dA} = \frac{J\frac{dA\cos\theta}{r^2}}{dA} = \frac{J\cos\theta}{r^2}
◦
High JJ, High EE
◦
Low θ\theta, High EE
◦
Low rr, High EE
•
Surface Radiance (LL)
◦
단위 면적, 단위 Solid Angle 당 방출되는 Light Flux (단위: W/m2⋅sr−1W/m^2\cdot sr^{-1})
◦
High Φ\Phi, High LL
◦
Low θ\theta, High LL
◦
Low AA, High LL
◦
Low dωd\omega, High LL

BRDF: Bidirectional Reflectance Distribution Function

f(θi,ϕi,θr,ϕr)=L(θr,ϕr)E(θi,ϕi)f(\theta_i, \phi_i, \theta_r, \phi_r) = \frac{L(\theta_r, \phi_r)}{E(\theta_i, \phi_i)}
•
BRDF 는 Surface Radiance 와 Surface Irradiance 의 비율
◦
Viewing, Illumination Angle 모두에 의존한 값임.
◦
θ\theta: Zenith, ϕ\phi: Azimuth
•
단위는 1/sr1/sr다
•
Surface 에 따라서 다음과 같은 다양한 형태의 BRDF 가 존재함.
◦
Surface Normal 을 얻기 위해서는 2D pixel value 와 관련이 있는 Illumination 을 이용하는데, 이 값은 BRDF 에 영향을 받는 값이고, 이 BRDF 를 결정짓는 물체의 property 를 아는 것이 중요함.
◦
보통은 Lambertian (Diffuse) 을 가정하고 문제를 해결하는 경우가 많음.

Diffuse & Specular Reflections

•
Diffuse Reflection: 모든 방향으로 동일하게 Light 를 분산시킴.
•
Specular Reflection: 특정 방향으로만 Light 를 반사시킴.
•
Combined: Diffuse Reflection 과 Specular Reflection 이 적당히 섞임.

Lambertian Reflectance Model for Body Reflection

f(θi,ϕi,θr,ϕr)=LE=ρ (Albedo)L=ρE=ρJr2(nˉ⋅sˉ)f(\theta_i,\phi_i,\theta_r,\phi_r)=\frac{L}{E}= \rho\ ({\rm Albedo}) \\ L=\rho E = \rho\frac{J}{r^2}(\bar{n}\cdot \bar{s})
•
Viewpoint 에 관계없이 같은 부분이면 같은 Illumination 으로 보이는 BRDF.
•
강한 assumption 이지만 동시에 대중적인 assumption 임.
•
ρ\rho 는 Albedo 로, 빛의 반사율이라고 볼 수 있음.
◦
검은색일수록 낮고, 흰색일수록 높음.
•
nˉ⋅sˉ\bar n \cdot \bar s 는 각각이 unit vector 라는 가정 하에 cos⁡θi\cos\theta_i 를 나타냄.
•
sˉ\bar s 의 방향과 Illumination LL, Light Power, Distance from the light, Albedo 등을 알면 Surface Normal 을 구할 수 있음.

Diffuse Reflection and Lambertian BRDF

L=ρE=ρJr2(nˉ⋅sˉ)L=\rho E = \rho \frac{J}{r^2}(\bar n \cdot \bar s)
•
동일한 광원과 동일한 거리를 가정하면, 오직 광원의 각도가 특정 부분에서 이미지의 픽셀값을 결정함.

Example of Lambertian Model

•
가장 밝은 지점 pp 는 광원의 방향과 동일한 곳임. (θi=0\theta_i = 0)
•
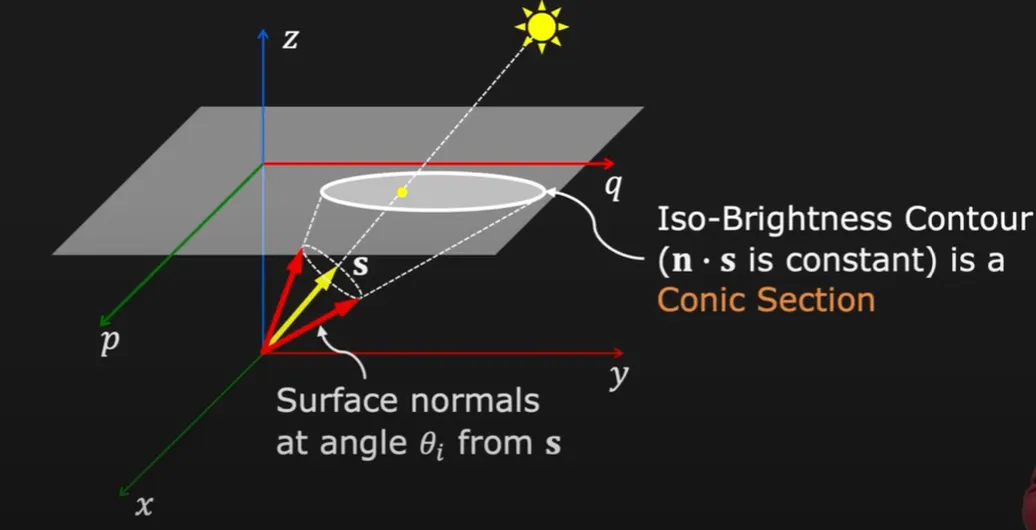
pp 근처로 동일한 거리의 원형 contour 는 밝기가 같음.
◦
cos⁡θi\cos\theta_i 값이 모두 동일한 점들이기 때문임.
◦
이러한 contour 를 Iso-Brightness Contour 라고 함.
◦
이 점들은 Brightness 가 같은데 Surface Normal 이 다르기 때문에 2D Image Pixel 정보만으로 Surface Normal 을 구하는데 ambiguity 를 부여하는 요소임.

Reflectance Map

•
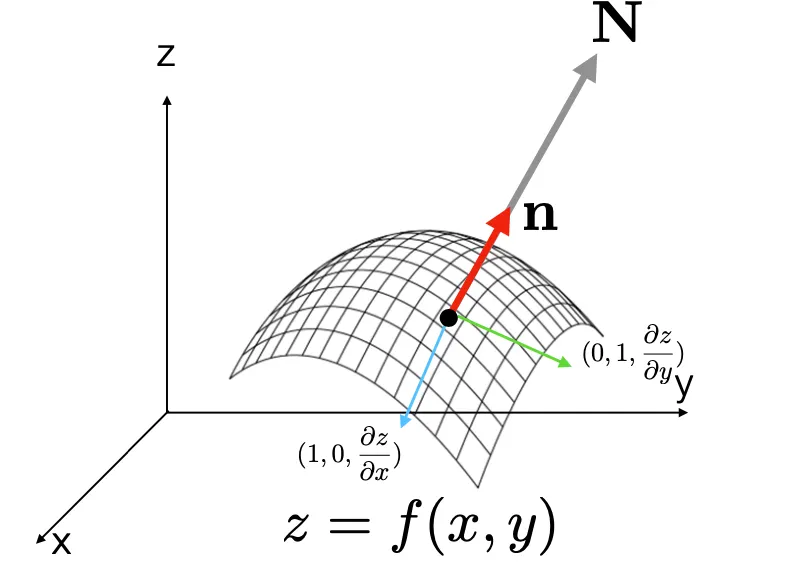
3D Shape 을 다음과 같이 z=f(x,y)z= f(x,y) 로 나타낼 수 있음.
•
xx 방향의 gradient 와 yy 방향의 gradient 는 다음과 같음.
p=−∂z∂xq=−∂z∂yp = -\frac{\partial z}{\partial x} \quad q = -\frac{\partial z}{\partial y}\\
•
Surface Normal Vector 는 다음과 같이 xx 방향의 tangential vector 와 yy 방향의 tangential vector 의 cross product 를 통해 구할 수 있음.
(1,0,∂z∂x)×(0,1,∂z∂y)=(−∂z∂x,−∂z∂y,1)=(p,q,1)(1,0,\frac{\partial z}{\partial x} )\times (0, 1, \frac{\partial z}{\partial y}) = (-\frac{\partial z}{\partial x},-\frac{\partial z}{\partial y},1) = (p,q,1)
•
Unit Surface Normal Vector 는 normalize 를 통해 다음과 같음.
n=N∥N∥=(p,q,1)p2+q2+1{\rm n} = \frac{{\rm N}}{\|{\rm N} \|}=\frac{(p, q,1)}{\sqrt{p^2 + q^2 +1}}

PQ Plane Representation

•
Surface Normal 은 p,qp,q 만으로 표현이 가능하고, z=1z=1 위의 평면 위의 점 하나로 Surface Normal 을 표현할 수 있음. 해당 평면 위의 점의 xx 좌표를 pp 로, yy 좌표를 qq 로 취급하면 됨.
•
이는 Light Source Direction Vector 에서도 동일하게 적용되어 다음과 같이 표현할 수 있음.
s=S∥S∥=(ps,qs,1)ps2+qs2+1{\rm s} = \frac{{\rm S}}{\| {\rm S}\|} = \frac{(p_s,q_s,1)}{\sqrt{p_s^2 + q_s^2 +1}}

Iso-Brightness Contours

L=ρJr2(nˉ⋅sˉ)L=\rho \frac{J}{r^2}(\bar n \cdot \bar s)
•
위 식에서 ρJr2=1\rho \frac{J}{r^2} = 1 가정을 도입하면 다음과 같은 식이 완성됨.
I=cos⁡θi=nˉ⋅sˉI=\cos\theta_i =\bar n \cdot \bar s
•
앞선 PQ Plane Representation 의 식을 도입하면 이는,
I=cos⁡θi=nˉ⋅sˉ=pps+qqs+1p2+q2+1ps2+qs2+1=R(p,q)I = \cos\theta_i = \bar n \cdot \bar s = \frac{pp_s + qq_s + 1}{\sqrt{p^2 + q^2 + 1}\sqrt{p_s^2 + q_s^2 + 1}} =R(p,q)
◦
결국 II 가 동일할 때의 p,qp,q 의 집합이 Iso-Brightness Contour 가 되고, R(p,q)R(p,q) 가 이들의 집합을 나타내는 식이 됨.
◦
이 Contour 는 conic 형태임.
•
우리가 해야하는 것은 특정 Brightness 를 가지는 다양한 p,qp,q 들 중 어떤 친구를 선택해야 정확한 Surface Normal 을 선택할 수 있는지 알아야 함.

Photometric Stereo

•
Known Point Light Source 를 세 개 이상 준비하여 각각에 따라 동일한 viewpoint 에서의 이미지를 이용해 3D Shape 을 얻어내는 방법
•
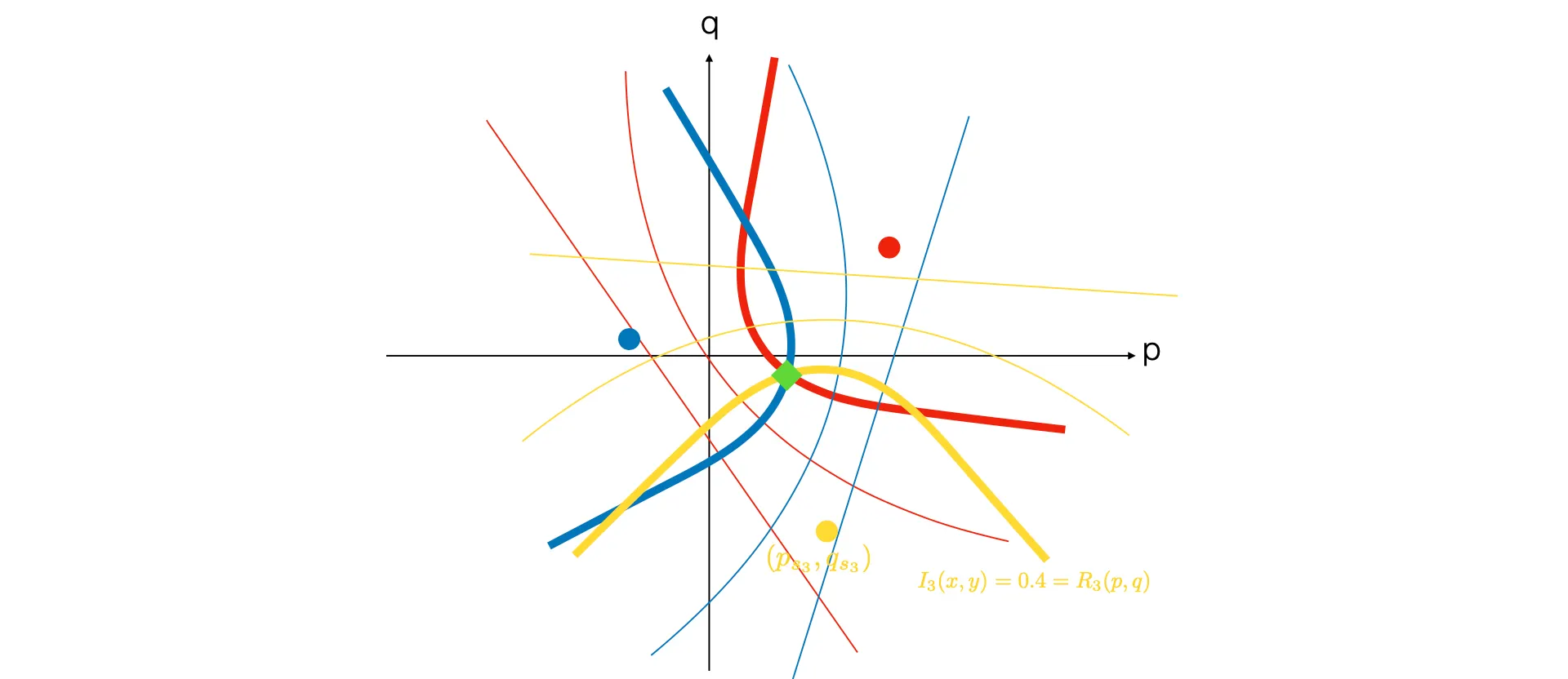
Corresponding Points 들에 대한 Brightness 를 각 이미지에서 구하고 (이 때, Corresponding Point 는 view point 가 같기 때문에 동일한 pixel 위치를 가짐…!), 각 이미지별로 Iso-Brightness Contour 를 그려 그 교점을 최종적인 해당 point 에서의 p,qp,q 값으로 선택하고, 이 값을 이용해 Surface Normal 을 계산할 수 있음.
•
수식적으로는 다음과 같이 구할 수 있음을 보일 수 있음.
I1=ρπn⋅s1I2=ρπn⋅s2I3=ρπn⋅s3I_1 = \frac{\rho}{\pi}{{\rm n}\cdot{\rm s}_1} \quad I_2 = \frac{\rho}{\pi}{{\rm n}\cdot{\rm s}_2} \quad I_3 = \frac{\rho}{\pi}{{\rm n}\cdot{\rm s}_3}
◦
이를 matrix form 으로 변경하면 다음과 같음.
[I1I2I3]=ρπ[sx1sy1sz1sx2sy2sz2sx3sy3sz3]nI=SN\begin{bmatrix} I_1 \\ I_2 \\ I_3 \end{bmatrix} = \frac{\rho}{\pi} \begin{bmatrix} s_{x_1} & s_{y_1} & s_{z_1} \\ s_{x_2} & s_{y_2} & s_{z_2} \\ s_{x_3} & s_{y_3} & s_{z_3} \\ \end{bmatrix} {\rm n} \\ \quad \\ I=S{\rm N}
◦
N=S−1I{\rm N} = S^{-1}I 를 통해 Surface Normal 의 방향을 구할 수 있고, Surface Normal Vector 와 Albedo 또한 구해낼 수 있음.
n=N∥N∥ρ=π∥N∥{\rm n} = \frac{{\rm N}}{\| {\rm N}\|} \quad {\rho} = \pi \| {\rm N}\|

Photometric Stereo for Ourdoor Webcam

•
Viewpoint 를 고정해두고 태양의 변화로 Photometric Stereo 를 돌릴 수 있음.
•
다만, light 가 planar 하게 들어오는 (??) case 에는 못 쓴다고 함…

Photogeometric Scene Flow for High-Detailed Dynamic 3D Reconstruction

•
R, G, B 를 동시에 쏴서 이미지 속에서 분리할 수만 있다면 물체가 고정되고 빛을 달리해야 할 필요가 없음.
◦
R, G, B 가 쏴져 캡처한 순간에 물체는 동일하기 때문임.