Duplicate

Lecture 26 | Classification II - SVM

수강 일자
2022/12/06

Procedure of Classification

1.
Gather Positive / Negative Training Data
2.
Feature Extraction
•
이미지로부터 p-dimensional vector 의 feature 를 뽑아냄
3.
Train Decison Boundary
•
p-dimensional space 에서 p-1 dimensional hyperplane 을 정의하여 양분함.

Decision Boundary (or Surface)

•
A Hypersurface that partitions the underlying feature space into two sets, one for each class
•
Hyperplane 은 Linear 한 Hypersurface 로, Ambient Space 보다 한 차원이 낮은 Hypersurface 의 Subspace 임.
•
Examples
◦
2차원 공간에서의 1차원 Hyperplane: ax+by+c=0ax+by+c = 0
◦
3차원 공간에서의 2차원 Hyperplane: ax+by+cz+d=0ax+by+cz + d =0
◦
4차원 공간에서의 3차원 Hyperplane: ax+by+cz+dw+e=0ax+by+cz+dw+ e =0
◦
Generalized Hyperplane
wTx+b=0w^Tx + b = 0
▪
w,bw,b 가 결정되면 Hyperplane 이 유일하게 결정됨.

Linear Decision boundary

•
wTx+b=0w^Tx +b=0 의 boundary 를 기준으로 한 쪽 영역은 0 보다 큰 값이, 다른 쪽 영역은 0 보다 작은 값이 나옴. (→ 양수면 Face, 음수면 Non-Face 로 prediction 을 만들 수 있음.)
•
Linearly Separable 한 데이터셋을 나누는 여러 Decision Boundary 중 어느 것이 optimal 할까?
◦
SVM: Margin (or Safe Zone) 을 가장 크게 하는 Decision Boundary 가 optimal
◦
SVM 의 학습은 Margin 을 Maximize 하는 과정

(Reminder) Point-Plane Distance

•
Given a plane: ax+by+cz+d=0ax+by+cz+d = 0
•
Normal Vector: v=[a,b,c]Tv =[a, b, c]^T
•
[x0,y0,z0]T[x_0,y_0,z_0]^T 와 Plane 상의 거리는 w=[x−x0,y−y0,z−z0]Tw=[x-x_0, y-y_0, z-z_0]^T 를 vv 방향으로 projection 한 값
D=v⋅w∥v∥=−a(x−x0)+b(y−y0)+c(z−z0)a2+b2+c2=ax0+by0+cz0+da2+b2+c2D = \frac{v \cdot w}{\| v\|} = - \frac{a(x-x_0) + b(y-y_0) + c(z-z_0)}{\sqrt {a^2 + b^2 +c^2}} = \frac{ax_0 + by_0 + cz_0 + d}{\sqrt {a^2 + b^2 +c^2}}
•
Line Equation 을 wTx+b=0w^Tx + b = 0 으로 나타낸 경우, 다음과 같이 거리를 나타낼 수 있음.
D=wTx0+b∥w∥D = \frac{w^Tx_0 + b}{\|w\|}

Linear SVM

•
Margin 을 정의할 수 있는 특정 점 xsx_s 부터 wTx+b=0w^Tx + b = 0 까지의 거리 ρ\rho 는 다음과 같음.
◦
c=wTxs+bc = w^Tx_s + b
ρ=wTxs+b∥w∥=c∥w∥\rho = \frac{w^Tx_s + b}{\| w\|} = \frac{c}{\|w\|}
•
Margin 을 최대화하는 것은 다음과 같이 나타낼 수 있음.
max⁡w2c∥w∥,s.t.wTxi+b∥w∥≥c∥w∥ ∀xi with yi=1 wTxi+b∥w∥≤−c∥w∥ ∀xi with yi=−1\begin{align*} &\max_w \frac{2c}{\|w\|},\\ &{\rm s.t.}\quad \frac{w^Tx_i + b}{\|w\|} \ge \frac{c}{\| w\|}\ \forall x_i\ {\rm with\ }y_i = 1 \\ & \quad\quad\ \frac{w^Tx_i + b}{\|w\|} \le \frac{-c}{\| w\|}\ \forall x_i\ {\rm with\ }y_i = -1 \end{align*}
◦
위의 Constraint 를 하나로 다음과 같이 간소화 할 수 있음.
max⁡w2c∥w∥,s.t.yiwTxi+b∥w∥≥c∥w∥ ∀i \max_w \frac{2c}{\|w\|}, {\rm s.t.}\quad y_i\frac{w^Tx_i + b}{\|w\|} \ge \frac{c}{\| w\|}\ \forall i
◦
Data Scaling 을 통해서도 동일한 결과를 얻을 수 있기 때문에 다음과 같이 변형할 수 있음.
min⁡w∥w∥,s.t. yi(wTxi+b)≥1 ∀i\min_w \|w\|, \quad {\rm s.t.}\ y_i(w^Tx_i+b) \ge 1\ \forall i
▪
Quadratic Programming (ww 에 대한 2차 함수와 linear constraint 를 가지는 문제) 을 해결하여 w,bw, b 를 구할 수 있음.

Non-Separable Data

•
Positive / Negative Sample 이 Linearly Separable 하지 않은 데이터
•
일반적으로 High Dimensional Problem (Data 개수보다 Dimension 의 개수가 많은 경우) 이라고 부르는 경우를 제외하면 자주 발생하는 문제임.
•
이러한 Non-Separable Data 의 경우에는 Soft Margin 을 도입함.
◦
각 데이터 point 마다 ξ\xi 로 표시하는, 얼마나 objective 를 어겼느냐를 나타내는 slack variable 을 둠.
◦
Objective 를 아래와 같이 변경함.
min⁡w∥w∥+C∑i=1Nξi,s.t. yi(wTxi+b)≥1−ξi and ξi≥0\min_w \|w \| + C\sum_{i=1}^N \xi_i, \quad {\rm s.t.}\ y_i(w^Tx_i+b) \ge 1 - \xi_i \ {\rm and}\ \xi_i \ge 0
▪
Constraint 에 ξi\xi_i 만큼 여유를 주는 대신, 여유를 주는 만큼을 최소한으로 작게 만들기 위해 objective 에 반영함.
▪
Wrong Side of Margin: Hyperplane 의 제대로 된 side 에 있지만, Margin 안쪽인 경우
▪
Wrong Side of Hyperplane: Hyperplane 의 올바르지 않은 side 에 있는 경우
▪
CC 를 작게 주면 데이터들이 Constraint 를 어기는 것에 대한 Penalty 가 없기 때문에 Margin 이 커지게 됨.
▪
CC 를 크게 주면 데이터들이 Constraint 를 어기는 것에 대한 Penalty 가 크기 떄문에 Margin 이 작아지게 됨.

Dual Form

•
The Duality Principle: Optimization Problem 은 두 개의 다른 관점으로 볼 수 있음.
◦
The Primary Form (Minimization Problem)
min⁡w∥w∥+C∑i=1Nξi,s.t. yi(wTxi+b)≥1−ξi, ξi≥0 for all i\min_w \|w\| + C\sum_{i=1}^N \xi_i, \quad {\rm s.t.\ } y_i(w^Tx_i+b) \ge 1- \xi_i,\ \xi_i \ge 0\ {\rm for\ all}\ i
◦
The Dual Form (Maximization Problem)
max⁡α∑i=1Nαi−12∑i=1N∑j=1Nαiαjyiyj(xiTxj)s.t. 0≤αi≤C for all i and ∑i=1Nαiyi=0\max_\alpha \sum_{i=1}^N \alpha_i - \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i\alpha_jy_iy_j(x_i^T x_j)\\ {\rm s.t.\ }0\le \alpha_i\le C\ {\rm for\ all\ } i\ {\rm and}\ \sum_{i=1}^N \alpha_iy_i = 0
▪
보통 Dual Form 이 수학적으로 해결하기 쉽고, Kernel Trick 을 사용할 수 있어 자주 사용됨.
▪
각 xix_i 가 Lagrange Multiplier αi\alpha_i 를 가짐.
▪
Support Vector 들이 αi>0\alpha_i > 0 이고 나머지 친구들은 αi=0\alpha_i =0 (Soft Margin 은 Constraint 를 어긴 데이터도 Support Vector 가 됨.)
▪
αi\alpha_i 를 구한 뒤, ww 는 다음과 같이 복원할 수 있음.
w=∑i=1Nαiyixiw = \sum_{i=1}^N \alpha_iy_ix_i
•
Support Vector 만 αi>0\alpha_i > 0 이기 때문에 해당 데이터만 고려하면 됨.
▪
ww 를 구하면 처음 Primary Form 으로 돌아가 다음 문제를 풀면 bb 를 구할 수 있음.
min⁡b∑i=1Nξi,s.t. yi(wTxi+b)≥1−ξi, ξi≥0 for all i\min_b \sum_{i=1}^N \xi_i, \quad {\rm s.t.}\ y_i(w^Tx_i+b)\ge 1-\xi_i,\ \xi_i \ge 0 \ {\rm for\ all\ } i
▪
Test 단에서는 sign(wTxt+b){\rm sign}(w^Tx_t + b) 를 구하면 됨.

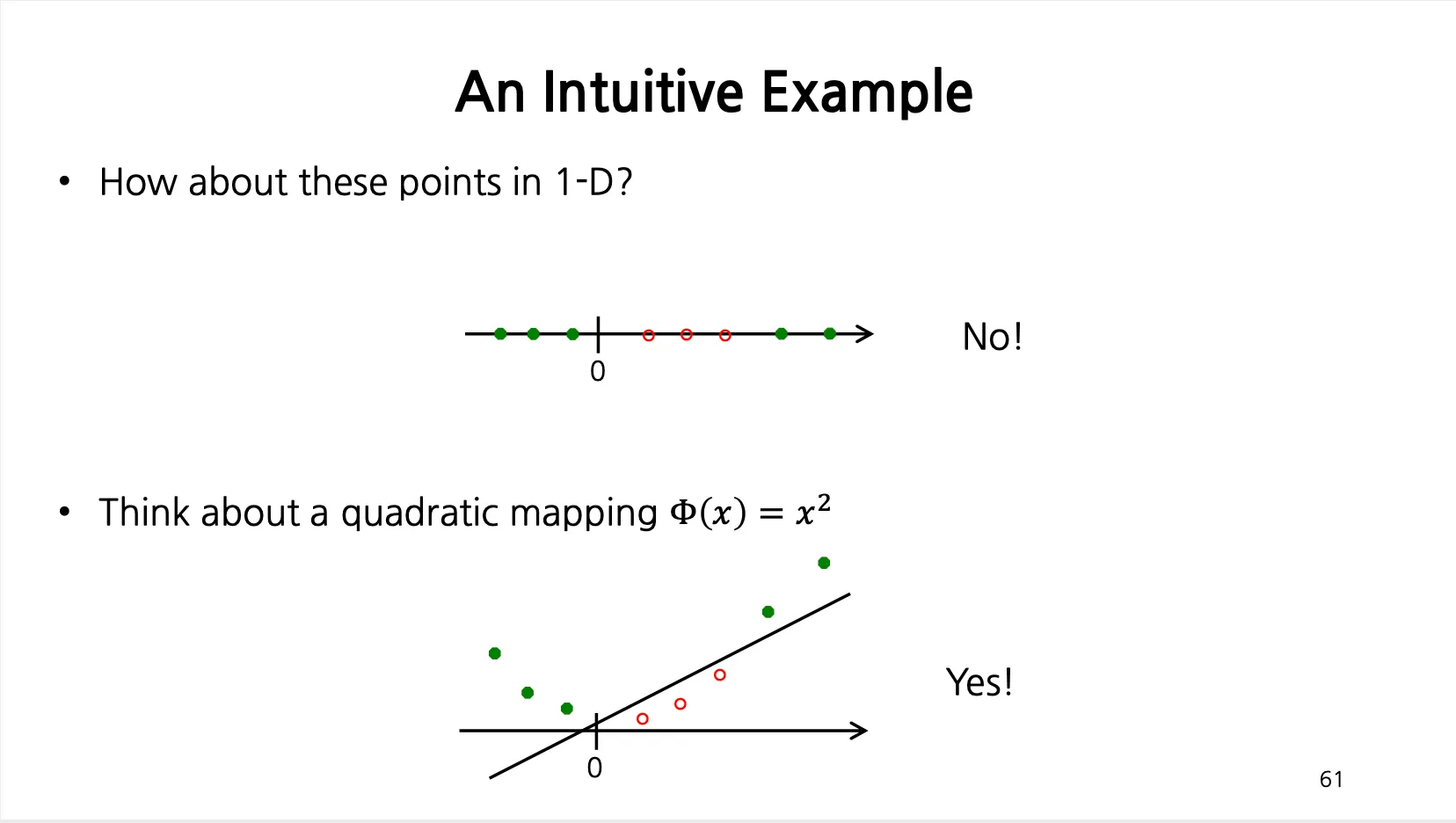
Linear Boundary Can Fail

•
선형적인 Decision Boundary 를 사용해서 실패하는 경우들이 있음.
•
다음과 같이 1-D 데이터를 quadratic mapping 을 하면 직선으로 나눌 수 있음.

Idea of Kernel Trick

•
데이터를 High Dimensional Space 로 mapping 하여 Linearly Separable 하게 만듬.
•
High Dimensional Space 에서의 Linear Decision Boundary 는 Original Space 에서 Non-Linear Decision Boundary 를 구현할 수 있는 방법이 됨.
•
Example
◦
Transformation function ϕ:R2→R3\phi: {\mathbb R^2 \rarr \mathbb R^3}
◦
x=[x1,x2]Tx = [x_1, x_2]^T, ϕ(x)=[x12,2x1,x2,x22]T\phi(x) = [x_1^2, \sqrt2 x_1,x_2, x_2^2]^T
◦
wTϕ(xi)+b=0w^T\phi(x_i)+ b = 0 → w1x12+w22x1x2+w3x22+b=0w_1x_1^2 + w_2 \sqrt2 x_1x_2 + w_3x_2^2 + b = 0
▪
(Non-Linear Decision Boundary)

Kernel Trick

max⁡α∑i=1Nαi−12∑i=1N∑j=1Nαiαjyiyj(xiTxj)s.t. 0≤αi≤C for all i and ∑i=1Nαiyi=0\max_\alpha \sum_{i=1}^N \alpha_i - \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i\alpha_jy_iy_j(x_i^T x_j)\\ {\rm s.t.\ }0\le \alpha_i\le C\ {\rm for\ all\ } i\ {\rm and}\ \sum_{i=1}^N \alpha_iy_i = 0
•
Dual Form 은 모든 데이터 사이의 dot product 를 필요로 함.
•
Kernel Trick 을 적용한다면, ϕ(xi),ϕ(xj)\phi(x_i), \phi(x_j) 에 대한 dot product 를 수행하는 것으로 볼 수 있음.
◦
ϕ(x)=[x12,2x1x2,x22]T\phi(x) = [x_1^2, \sqrt2 x_1x_2, x_2^2]^T 에 대해서, (xiTxj)2=ϕ(xi)Tϕ(xj)(x_i^Tx_j)^2 = \phi(x_i)^T\phi(x_j) 를 만족함.
◦
Dot product 를 2차원에서 수행하고 제곱하는 것이 훨씬 효율적임.
▪
Kernel Trick: 2 Multiplication + 1 Summation + Scalar Square (1 Multiplication)
▪
Original: Square of 2 Vector (3 Multiplication + 3 Multiplication) + 1 Dot Product (3 Multiplication + 2 Summation)
▪
위 차이가 N(N−1)/2N(N-1)/2 만큼 반복해서 차이가 굉장히 커짐
•
실제로는 제곱까지 포함한 Kernel Function K(xi,xj)K(x_i,x_j) 를 다음과 같이 정의함.
K(xi,xj)=(xiTxj)2=⟨xi,xj⟩2K(x_i,x_j) = (x_i^Tx_j)^2 = \left\langle x_i, x_j \right\rangle^2
◦
Original Feature Space 에서 dot product 진행 후 scalar 를 제곱함.
◦
유명한 Kernel Functions 들
▪
Polynomial
▪
RBF (Radial Basis Function)
▪
Sigmoid
▪
Histogram 형태 → Chi-Square, Histogram Intersections

Kernel Functions

•
Polynomial Kernel
K(xi,xj)=(xiTxj+1)dK(x_i,x_j) = (x_i^Tx_j + 1) ^d
◦
DdD^d 개의 feature 로 확장할 수 있음. (DD: original space dimension)
•
RBF Kernel (Gaussian Kernel)
K(xi,xj)=exp⁡(−∥xi−xj∥22σ2)=exp⁡(−γ∥xi−xj∥2)K(x_i,x_j) = \exp(-\frac{\|x_i-x_j\|^2}{2\sigma^2}) = \exp(-\gamma\|x_i-x_j\|^2)
•
Sigmoid Kernel
K(xi,xj)=tanh⁡(axiTxj+r)K(x_i,x_j) = \tanh(ax_i^Tx_j + r)
◦
자주 쓰이는 Kernel 은 아님.
•
어떤 Kernel Function 을 쓸 것인가 + Hyperparameter 등을 어떻게 설정할 것인가는 데이터가 주어졌을 때 다양하게 시도해보는 수 밖에 없음.

Kernel Functions for Histogram

•
Histogram Intersection Kernel
K(xi,xj)=∑d=1Dmin⁡(xi,d,xj,d)K(x_i,x_j) = \sum_{d=1}^D \min(x_{i,d}, x_{j,d})
◦
각 벡터의 항목마다 i,ji,j 중 작은 것을 선택하여 구성함. (두 histogram 상의 교집합을 찾는 효과)
•
Chi-Square Kernel
K(xi,xj)=exp⁡(−1γ∑d=1D(xi,d−xj,d)2xi,d+xj,d)K(x_i,x_j) = \exp(-\frac{1}{\gamma}\sum_{d=1}^D \frac{(x_{i,d}-x_{j,d})^2}{x_{i,d}+ x_{j,d}})
◦
Histogram 의 각 항목마다 뺀 값을 제곱하고 두 항목을 더한 것으로 나누어줘서 새로운 값을 구성함.
◦
시간이 오래걸려 일반적으로 Computer Vision 에서 많이 쓰이지는 않음.

Choosing a Kernel

•
Linear: Fast Training/Test - Start Here!
•
RBF
•
Chi-Squared, Histogram Intersection: Good for Histograms
•
Kernel Learning → Kernel Function 을 배우는 방법론

Summary of SVM

•
Classification 을 할 때 가장 많이, 안정적으로 쓸 수 있는 방법론
•
딥러닝 나오기 전에 Random Forest 와 함께 많이 사용되었고, 딥러닝 나온 후에도 Softmax 대신에 SVM 을 사용하기도 했음.