Duplicate

Lecture 12 | Calibration

수강 일자
2022/10/17

Modeling Projection

•
(x,y,z)→(fxz,fyz)(x,y,z)\rarr (f\frac{x}{z},f\frac{y}{z})

Homogeneous Coordinates

•
Camera Coordinate (x,y,z)→(fxz,fyz)(x,y,z)\rarr (f\frac{x}{z},f\frac{y}{z}) 로 매핑할 때 하나의 Matrix Multiplication 으로 표현하고자 함
◦
A[xyz]=[fxzfyz]A \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} f\frac{x}{z} \\ f\frac{y}{z} \end{bmatrix}인 AA 는 zz 에 대한 division 을 구현할 수 없어서 존재하지 않음.
•
각 좌표의 끝에 11 을 추가하는 형태의 표현방식인 Homogeneous Coordinate 를 사용
(x,y)→[xy1], (x,y,z)→[xyz1],(x,y) \rarr \begin{bmatrix} x \\ y \\ 1 \end{bmatrix},\ (x,y, z) \rarr \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix},
•
Homogeneous Coordinate 에서 Cartesian Coordinate 로 변환할 때는 마지막 항목으로 나머지 값들을 나누어주면 됨.
◦
이 나누기를 통해 zz 에 대한 division 을 구현할 수 있음

Perspective Projection Matrix

[10000100001/f0][xyz1]=[xyz/f]→(fxz,fyz)\begin{bmatrix} 1 & 0&0&0 \\ 0 & 1&0&0 \\ 0 & 0&1/f&0 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \\ \end{bmatrix} = \begin{bmatrix} x \\ y \\ z/f \\ \end{bmatrix} \rarr (f\frac{x}{z},f\frac{y}{z})

Orthographic Projection

•
Perspective Projection 의 특수한 경우
◦
z>>Δzz >> \Delta z
▪
Δz\Delta z 는 피사체의 두께
▪
zz 는 Camera Center 와 피사체와의 거리
◦
Telepho Optics 의 좋은 approximation
•
Camera Center 를 통과하게 그리는 것이 아니라 평행하게 선을 이어 상이 맺힌다고 봄
◦
Real World 의 dimension 이 Image Plane 에 그대로 적용됨
◦
Sim City 같은 게임을 할 때 앞 건물이 뒷 건물보다 커야하는데, 게임하기 편하기 위해서 이를 고려하지 않고 비율이 같음 (Perspective Effect 를 무시함)
•
Projection Matrix
[100001000001][xyz1]=[xy1]→(x,y)\begin{bmatrix} 1 & 0&0&0 \\ 0 & 1&0&0 \\ 0 & 0&0&1 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \\ \end{bmatrix} = \begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix} \rarr (x,y)
•
Scaled Orthographic Projection Matrix
◦
Orthographic Projection 에 scale 을 입힌 것 (피사체와 Camera Center 와의 거리나 Effective Focal Length 에 관계없이 비율은 동일하지만, 그 동일한 비율의 크기를 조절)
◦
Weak Perspective 이라고도 부름.
[100001000001/d][xyz1]=[xy1/d]→(dx,dy)\begin{bmatrix} 1 & 0&0&0 \\ 0 & 1&0&0 \\ 0 & 0&0&1/d \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \\ \end{bmatrix} = \begin{bmatrix} x \\ y \\ 1/d \\ \end{bmatrix} \rarr (dx,dy)
•
Affine Projection
◦
구체적으로 다루지는 않음.
[abcdefgh0001][xyz1]\begin{bmatrix} a & b&c&d \\ e & f&g&h \\ 0 & 0&0&1 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \\ \end{bmatrix}

Camera Model

•
3D World Coordinate P(x,y,z)P(x,y,z) 를 2D Image Plane 상의 (u,v)(u,v) 로 변환하는 과정
•
고려할 세 가지 Coordinate System
◦
World Coordinate: 3D Point 가 정의된 Coordinate
◦
Camera Coordinate: 3D Point 를 2D Point 로 변환하는 Coordinate (zz 축이 Image Plane 에 수직)
◦
Image Coordinate: Image Plane 의 점이 Pixel 로 변환된 Coordinate

Pinhole Camera Model

•
World: Extrinsic/External Camera Parameters (3D World Coordinate → 3D Camera Coordinate)
◦
임의의 3차원 → 3차원 좌표변환을 표현하는 방법
◦
Euler Transformation
Xc=RXw+T[RT0T1][XwYwZw1]=[XcYcZc1]X_c=RX_w+T \\ \begin{bmatrix} R & T \\ 0^T & 1 \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix} = \begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \end{bmatrix}
•
Camera: Perspective Projection (3D Camera Coordinate → 2D Image Coordinate)
[f0000f000010][XYZ1]=[xy1]\begin{bmatrix} f & 0&0&0 \\ 0 & f&0&0 \\ 0 & 0&1&0 \\ \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ 1 \\ \end{bmatrix} = \begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix}
◦
앞의 3×43\times 4 Perspective Transform Matrix 는 3×33\times 3 Rotation Matrix 와 3×13\times1 Translation Vector 로 나누어 이야기하기도 함.
•
Image: Intrinsic/Internal Camera Parameters (2D Image Coordinate → Pixel 2D Image Coordinate)
◦
Image Plane 상의 Principal Point (Image Plane 의 중심점) 가 Image Coordinate 기준으로 (u0,v0)(u_0,v_0) 라고 할 때, 길이를 Image Coordinate 의 pixel 로 변환하면 다음과 같음.
u=kux+u0v=kvy+v0u=k_ux+u_0 \\ v=k_vy+v_0 \\
◦
Homogeneous Coordinate
▪
여러 오차에 의해서 Image Plane 이 찌그러질 수 있고, 이를 보정하기 위한 parameter 가 ss
▪
Skew 가 없다고 가정하면 s=0s=0
[kusu00kvv0001][xy1]=[uv1]\begin{bmatrix} k_u & s &u_0 \\ 0 & k_v & v_0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix} = \begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix}
▪
kuk_u, kvk_v, u0u_0, v0v_0, ss 는 Internal Parameter 라고 하고, 이들로 구성된 좌측 Matrix 가 Internal Matrix
◦
Practical Camera 에는 Radial Distortion 이 존재하여 보정하는 과정이 필요할 수 있음
▪
Lens 바깥쪽을 통과하는 ray 는 deviation 이 많음
•
Wrap-up
◦
3D World Coordinate (4×14\times1) → 3D Camera Coordinate (4×14\times 1) → 2D Image Plane Coordinate (3×13\times 1) → 2D Pixel Image Coordinate (3×13\times 1)
◦
x=A[R ∣ t]Xx = A[R\ |\ t] X
[uv1]=[ku0u00kvv0001][f0000f000010][RT0T1][XwYwZw1]\begin{bmatrix} u \\ v \\ 1 \end{bmatrix}= \begin{bmatrix} k_u & 0 & u_0 \\ 0 & k_v & v_0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0\\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} R & T \\ 0^T & 1 \end{bmatrix} \begin{bmatrix} X_w \\ Y_w\\ Z_w \\ 1 \end{bmatrix}
◦
최종적인 Multiplication Matrix 는 3×43\times4 이며 DOF 는 11 임. (배수를 곱한 Matrix 는 동일하게 취급되기 때문)

Modeling Distortion

•
World Coordinate 의 (X,Y,Z)(X,Y,Z) 에서 XX, YY 를 ZZ 로 나누어 xnx_n, yny_n 을 구함.
xn=XZ, yn=YZx_n=\frac{X}{Z},\ y_n=\frac{Y}{Z}
•
Radial Distortion 을 적용함.
r2=xn2+yn2r^2=x_n^2 +y_n^2
xd=xn(1+κ1r2+κ2r4)yd=yn(1+κ1r2+κ2r4)x_d=x_n(1+\kappa_1r^2+\kappa_2r^4) \\ y_d=y_n(1+\kappa_1r^2+\kappa_2r^4)
•
Focal Length 를 곱하고 Camera Center 를 더해줘서 최종적인 변환을 구해냄.
x=fxd+xcy=fyd+ycx=fx_d+x_c\\ y=fy_d+y_c\\

Camera Calibration

•
Intrinsic Parameter 와 Extrinsic Parameter 를 알아내는 과정
◦
Intrinsic Parameter: Focal Length, Optical Center, Skew …
◦
Extrinsic Parameter: Rotation, Translation
•
최종적으로는 DOF 인 11 개의 parameter 를 찾아내야 함.
[uv1]=[abcdefghijk1][XYZ1]\begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \begin{bmatrix} a & b & c & d \\ e & f & g & h \\ i & j & k & 1 \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ 1 \end{bmatrix}
◦
11 개의 (Xi,Yi,Zi,1)(X_i,Y_i,Z_i,1) 과 (ui,vi,1)(u_i, v_i,1) 의 쌍이 있으면 결정할 수 있음
ui=aXi+bYi+cZi+diXi+jYi+kZi+1, vi=eXi+fYi+gZi+hiXi+jYi+kZi+1u_i=\frac{aX_i+bY_i+cZ_i+d}{iX_i+jY_i +kZ_i+1}, \ v_i=\frac{eX_i+fY_i+gZ_i+h}{iX_i+jY_i +kZ_i+1}
◦
수식을 변경해 unkown 만을 vector 로 뽑아낼 수 있음
[XiYiZi10000−uiXi−uiYi−uiZi0000XiYiZi1−viXi−viYi−viZi][abcdefghijk]=[uivi]\begin{bmatrix} X_i & Y_i & Z_i & 1 & 0 & 0 & 0 & 0 & -u_iX_i & -u_iY_i & -u_iZ_i \\ 0&0&0&0&X_i&Y_i&Z_i&1&-v_iX_i&-v_iY_i&-v_iZ_i \end{bmatrix} \begin{bmatrix} a \\ b \\ c \\ d \\ e \\ f \\ g \\ h \\ i \\ j \\ k \end{bmatrix} = \begin{bmatrix} u_i \\ v_i \end{bmatrix}
▪
n 개의 쌍을 쌓으면 At=bAt=b 에서 AA 는 2n×112n\times 11 이 되고, bb 는 2n×12n \times 1 이 된 형태의 식으로 표현할 수 있음
▪
Residual ϵ=∥At−b∥2\epsilon = \|At-b \|^2 를 최소화하도록 parameter 를 찾도록 함
∥At−b∥2=(At−b)T(At−b)=bTb−tTATb−bTAt+tTATAt=bTb−2tTATb+tTATAt\begin{align*} \|At-b\|^2 &= (At-b)^T(At-b)\\ &= b^Tb -t^TA^Tb-b^TAt+t^TA^TAt \\ &= b^Tb-2t^TA^Tb+t^TA^TAt \\ \end{align*}
•
미분해서 0 이 되도록 하는 값을 찾아봄
−2ATb+2ATAt=0ATAt=ATbt=(ATA)−1ATb-2A^Tb+2A^TAt = 0 \\ A^TAt = A^Tb \\ t = (A^TA)^{-1}A^Tb
•
Non-Linear Regression 으로도 11 개의 parameter 를 찾을 수 있음.
◦
Levenberg-Marquardt 방법론을 사용하여 다음을 촤소화할수 있음.
◦
강의에서 디테일하게 다루지는 않음.
∑i=1n(ui−aXi+bYi+cZi+diXi+jYi+kZi+1)2+(vi−eXi+fYi+gZi+hiXi+jYi+kZi+1)2\sum_{i=1}^n (u_i-\frac{aX_i+bY_i+cZ_i+d}{iX_i+jY_i +kZ_i+1})^2 + (v_i-\frac{eX_i+fY_i+gZ_i+h}{iX_i+jY_i +kZ_i+1})^2

Practical Issue (for obtaining data for calibration)

•
Multi-Plane Calibration
◦
Checkerboard Plane 을 준비하고, 해당 Checkerboard 의 한 칸 길이만 알고 있어야 함.
◦
Checkerboard 를 들고 여러 장의 사진을 찍으면 Toolbox 를 사용해 Intrinsic/Extrinsic Parameters 들을 구할 수 있음.
◦
Step 1: Data Acquisition: Planar Checkerboard 사진을 많이 찍음.
◦
Step 2: Checkerboard 의 네 꼭지점을 클릭함.
▪
안쪽의 corner 들은 자동으로 구해짐.
◦
Step 3: Iterate Corner Detection
◦
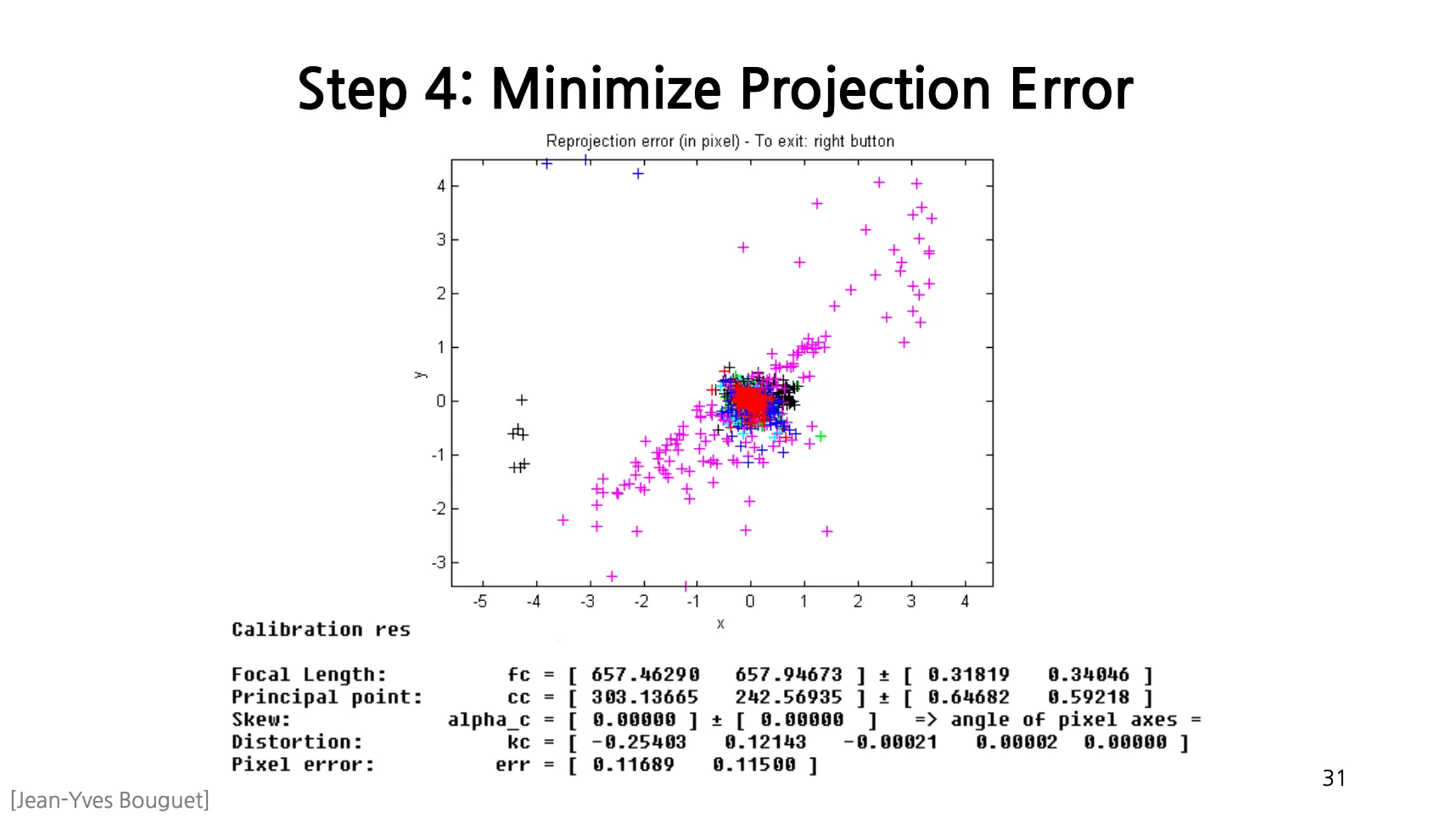
Step 4: Minimize Projection Error
▪
Non-Linear Optimization 을 통해서 각 parameters 들을 자동으로 구해줌.

Summary

•
Calibration 은 Camera Model 의 Intrinsic/Extrinsic Parameter 를 찾아내는 과정임.
•
Intrinsic Parameter 는 Camera 에 의존적인 parameter 로 카메라가 바뀌면 따라서 바뀜.
◦
이를 알게 되면 Lens Distortion 등을 보정할 수도 있음.
•
Extrinsic Parameter 는 3D World Coordinate 를 3D Camera Coordinate 로 바꾸는 과정이어서 카메라의 위치랑 방향이 고정되면 고정됨.
•
Calibration 에 대해서 잘 알려면 Optimization 에 대해서도 잘 알 필요가 있음.