Duplicate

Lecture 6 | Robust Estimation & 3D Projective Geometry

수강 일자
2023/02/25

Homography - Practical Applications

•
Corresponding Point 를 찾기 위해 SIFT Descriptor 를 사용할 수 있음.
◦
SIFT Descriptor 는 realiably “identifiable” points 를 feature points 들로 찾아줌.
•
하지만, SIFT Descriptor 는 생각보다 outlier 를 많이 뽑아줌.
◦
이러한 outlier 들을 homography 를 계산하는데 사용하면 부정확한 값이 나옴.
◦
이러한 outlier 를 줄여주는 방법론이 RANSAC 임.

RANSAC

•
두 점 x1,x2{\rm x_1, x_2} 를 이용해 line 을 fitting 하는 방법은 단순하게 cross product 도 있지만, 다음과 같이 Null Space (의 vector)를 구하는 것도 존재함.
[x1Tx2T]l=0\begin{bmatrix} {\rm x_1}^T \\ {\rm x_2}^T \end{bmatrix}{\rm l} = 0
◦
이 방법은 측정에 noise 가 있더라도 대강의 Null Space 를 구해낼 수 있다는 장점이 있음.
•
RANSAC 의 프로세스는 다음과 같음.
1.
랜덤하게 두 개의 점을 선택함.
2.
두 개의 점을 이용해 그은 선에서 threshold 안에 몇 개의 점이 있는지 세고 이들을 inlier 로 선언함.
3.
특정 iteration 만큼 돌았을 때 가장 많은 inlier 를 가졌던 두 개의 점을 best case 로 설정함.
4.
Best case 에서 inlier 들을 이용해 Null Space fitting 을 진행함.
•
RANSAC 의 성공확률 ?
p=1−(1−αn)kp=1-(1-\alpha^n)^k
◦
pp 는 success probability
◦
α\alpha 는 전체 sample 중 inlier sample 의 개수
◦
nn 은 model 을 estimating 할 때 사용되는 sample 의 개수
◦
kk 는 number of iteration
◦
RANSAC 은 다음 상황에서 잘 동작함.
1.
다수의 sample 들이 inlier 여야 함. (α\alpha 가 커야 함.)
2.
Iteration 이 충분하게 많아야 함. (kk 가 커야 함.)
3.
시스템의 DoF 가 작아야 함. (nn 이 작아야 함.)
◦
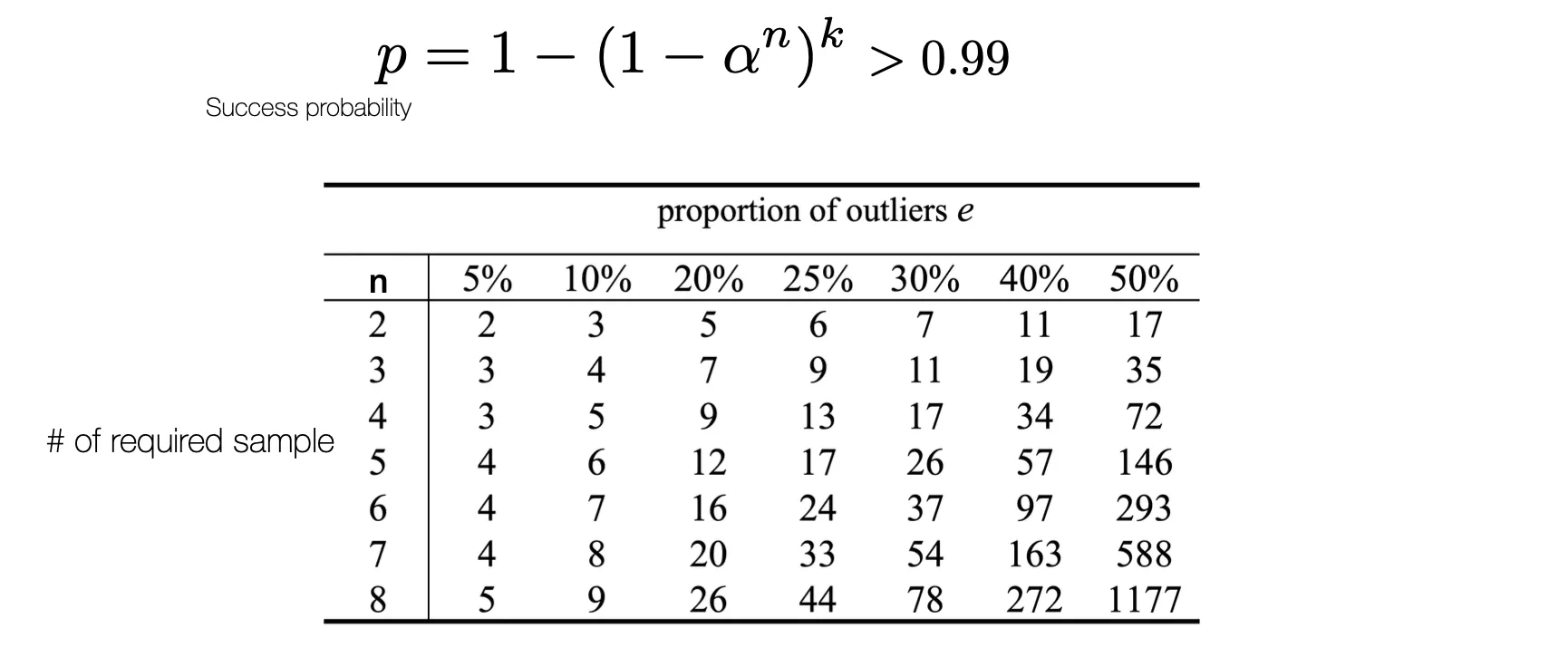
아래는 성공확률을 0.99 이상으로 높이기 위해 필요한 sample 수임.
▪
Outlier 를 줄이는 것이 필요한 sample 수를 급격히 줄이는 것을 알 수 있음. → RANSAC 의 중요성을 알 수 있는 대목임.
•
Pros and Cons
◦
Pros
▪
실제 세팅에서 잘 동작함.
▪
많은 3D Vision Application 에서 처음으로 고려되는 옵션임.
◦
Cons
▪
실행이 느림.
▪
보장이 없음.
▪
Treshold 나 iteration 같은 parameter 에 대한 조절이 필요함.

Homography - Practical Applications

•
RANSAC iteration process 를 다음과 같이 진행함.
1.
랜덤하게 4 개의 점을 고름.
2.
DLT 를 이용해 H{\rm H} 를 계산함.
3.
계산한 H\rm H 로 inlier 수를 계산함.
•
가진 Corresponding Points 들에 대해서∥Hx−x′∥\|{\rm H}{\rm x} - {\rm x}'\| 의 distance 를 계산하고 해당 distance 가 threshold 를 넘는지 아닌지를기준으로 inlier 와 outlier 를 나눔.
•
특정 iteration 반복 후 가장 많은 inlier 를 가졌던 점들을 이용해 DLT 를 사용함.

Algebraic Error Vs. Geometric Error

•
DLT 를 활용하는 것은 Algebraic Error 를 최소화하는 것임.
Ah=0h∗=arg min⁡h∥Ah∥subject to ∥h∥=1{\rm A}{\rm h} = 0 \\ h^* = \argmin_{\rm h}\|{\rm A}{\rm h}\| \quad {\rm subject\ to}\ \|{\rm h} \| = 1
◦
사실 Ah{\rm Ah} 항목이 무엇을 의미하는지에 대한 것을 설명할 수 없기 때문에 최소화하는 것의 정성적인 의미는 없음
•
하지만, 실제로 Homography 의 계산은 모든 대응점들의 오류를 최소화하는 구체적인 목표가 있음.
H∗=arg min⁡H∑id(Hxi,xi′){\rm H}^* = \argmin_{\rm H}\sum_i d({\rm H}{\rm x}_i, {\rm x}'_i)
◦
때문에 보통은 DLT 를 활용한 Algebraic Error 의 최소화를 통해 inital H{\rm H} 를 정하고, optimization method (e.g. gradient descent) 를 사용하게 됨.

3D Projective Geometry P3\mathbb P^3

•
3D point in Homogeneous Coordinate 는 다음과 같이 표현할 수 있음.
X=(x1,x2,x3,1)T=[x1x2x31]{\rm X} = (x_1,x_2,x_3,1)^T = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ 1 \end{bmatrix}
•
3D plane 은 2D plane 때와 마찬가지로 동일한 형태로 표현이 가능함.
π=(π1,π2,π3,π4)Tπ1x1+π2x2+π3x3+π4x4=0↔πTX=0{\pi} = (\pi_1, \pi_2, \pi_3, \pi_4)^T \\ \pi_1x_1 + \pi_2x_2 + \pi_3x_3 + \pi_4x_4 = 0 \lrarr \pi^T{\rm X} = 0
•
Conic → Quadric ?
◦
Sphere, Ellipsoid, Hyperboloid, Parabolid
XTQX=0{\rm X}^TQ{\rm X} = 0

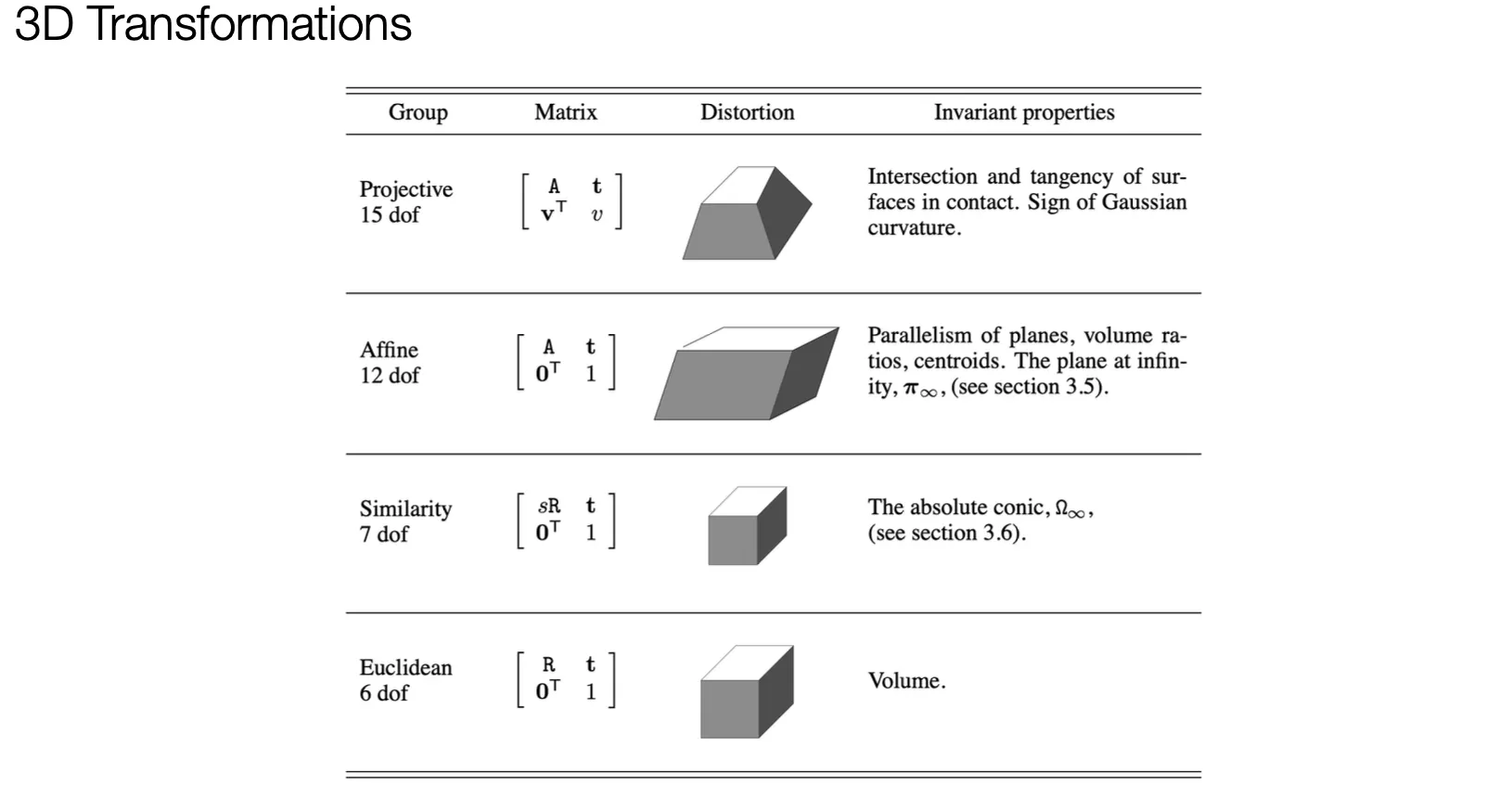
A Hierarchy of Transformations in 3D

•
Euclidean
◦
6DoF: Rotation(3DoF) + Translation(3DoF)
•
Similarity
◦
7DoF: Scalar(1DoF) + Rotation(3DoF) + Translation(3DoF)
•
Affine
◦
12DoF: A(9DoF) + Translation(3DoF)
◦
Parallelism of Plane 을 유지함.
•
Projective
◦
15DoF: 16DoF - 1DoF (Up-to-Scale)

Plane at Infinity

π∞=(0,0,0,1)T\pi_{\infty} = (0,0,0,1)^T
•
Plane at Infinity 위에 있는 점들은 모두 Point at Infinity 임.
◦
두 개의 line 이 평행하면, 그들의 intersection 인 점은 Plane at Infinity 위에 있음.
◦
두 개의 line 의 intersection 이 Plane at Infinity 위에 있으면 이 둘은 평행함.
•
Plane at Infinity 위에 있는 선들은 모두 Line at Infinity 임.
◦
두 개의 plane 이 평행하면, 그들의 intersection 인 선은 Plane at Infinity 위에 있음.
◦
두 개의 plane 의 intersection 이 Plane at Infinity 위에 있으면 이 둘은 평행함.
•
Plane at Infinity 는 Affine Transformation 에 invariant 함.

Absolute Conic Ω∞\Omega_{\infty}

•
Circular Points 와 동일하게 Similarity Transformations 에 invariant 함.
•
Absolute Conic 의 정의는 다음과 같음.
x12+x22+x32=0x4=0{\rm x_1}^2 + {\rm x_2}^2 + {\rm x_3}^2 = 0 \\ {\rm x_4} = 0
◦
위의 첫 번째 식은 다음과 같이 표현할 수도 있음.
(x1,x2,x3)I(x1,x2,x3)T=0({\rm x_1}, {\rm x_2}, {\rm x}_3){\rm I}({\rm x_1}, {\rm x_2}, {\rm x}_3)^T = 0
◦
때문에 Absolute Conic 자체를 Identity Matrix 로 표현함.
Ω∞=I=[100010001]\Omega_{\infty} = {\rm I} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}
◦
두 개의 3D ray 방향 d1,d2d_1, d_2 에 대해서 다음과 같은 식이 성립함.
cos⁡θ=d1TΩ∞d2(d1TΩ∞d1)(d2TΩ∞d2)\cos\theta = \frac{d_1^T\Omega_{\infty}d_2}{\sqrt{(d_1^T\Omega_{\infty}d_1)(d_2^T\Omega_{\infty}d_2)}}
•
Properties ?
◦
Plane at Infinity π∞\pi_{\infty} 와 일반적인 plane π\pi 와의 교점은 선인데, 이 선은 Absolute Conic Ω∞\Omega_\infty 와 plane π\pi 에서 정의되는 Circular Points 에서 만남.
▪
Absolute Conic Ω∞\Omega_\infty 와 plane π\pi 모두 Point at Infinity 인 Circular Point 를 포함하기 때문임.
◦
모든 circle 은 Absolute Conic Ω∞\Omega_\infty 와 두 개의 점 (Circular Points) 에서 만남.
◦
모든 sphere 는 π∞\pi_\infty 와 Absolute Conic Ω∞\Omega_\infty 에서 만남.

Absolute Dual Quadric

•
정성적으로는 Absolute Conic 에 접하는 plane 들이 만드는 quadric 을 의미함. (????)
•
Degenerated Dual Quadric 은 다음과 같음.
Q∞∗=[I00T0]Q^*_{\infty} = \begin{bmatrix} {\rm I} & 0 \\ 0^T & 0 \end{bmatrix}
•
두 개의 plane 간의 각도를 위의 quadric 을 사용해 나타낼 수 있기 때문에 중요함.
cos⁡θ=π1TQ∞∗π2(π1TQ∞∗π1)(π2TQ∞∗π2)\cos\theta = \frac{\pi_1^TQ^*_{\infty}\pi_2}{(\pi_1^TQ^*_{\infty}\pi_1)(\pi_2^TQ^*_{\infty}\pi_2)}
◦
3D reconstruction 의 noisiness 를 rectify 하는데 사용되기도 함.