Iso-Points: Optimizing Neural Implicit Surfaces with Hybrid Representations

리뷰 날짜
2022/08/04
분야
3D Model Representation
본 포스트에서는 Implicit Surface 에 그로부터 생성한 Explicit 3D Model 더해 Hybrid 3D Model Representation 을 완성하여 해당 3D Model 의 표현이 optimization 에 유의미함을 입증한 논문에 대해서 소개드리려고 합니다.
“Iso-Points: Optimizing Neural Implicit Surfaces with Hybrid Representations”
논문에 대한 내용을 직접 보시고 싶으신 분은 이곳을 참고하시면 좋습니다.

Objective

다양한 관점에서 관측한 이미지 (Multi-View Image 라고 합니다.) 나 Point Cloud 와 같은 노이즈가 있는 실 관측 데이터로부터 본래의 3D Model 을 재구성하는 것은 Computer Vision 영역의 오랜 과제 중 하나였습니다.
최근에는 이러한 3D Model Reconstruction 분야에서 사용할 3D Model Representation 으로 Point Cloud, Mesh, Voxel Grid 와 같은 Explicit Representation 과 비교해서 비교적 제한적이지 않고, 다양하면서도 구체적인 3D 형태를 표현할 수 있는 장점을 가진 Neural Implicit Function 이 주목을 받고 있습니다.
Neural Implicit Function ? 3D 데이터를 표현하는 방법론 중 하나로, Neural Network 가 하나의 Neural Implicit Function 의 역할을 합니다. 해당 네트워크는 x, y, z coordinate 를 input 으로 받아 하나의 floating number 를 산출하는데, 이 값이 해당 coordinate 로 부터 표현하려는 3D Model 의 Surface 까지의 거리(Signed Distance, Unsigned Distance 등) 를 의미합니다. 산출값이 0 인 coordinate 들의 집합이 Implicit Surface 가 되는 것입니다.
하지만, Neural Implicit Surface 를 노이즈가 있는 관측 Point Cloud 나 Multi-View Image 들에 맞게 fitting 하여 재구성하는 작업은 네트워크가 불완전한 결과로 학습되는 결과로 이어지는 경우가 많습니다.
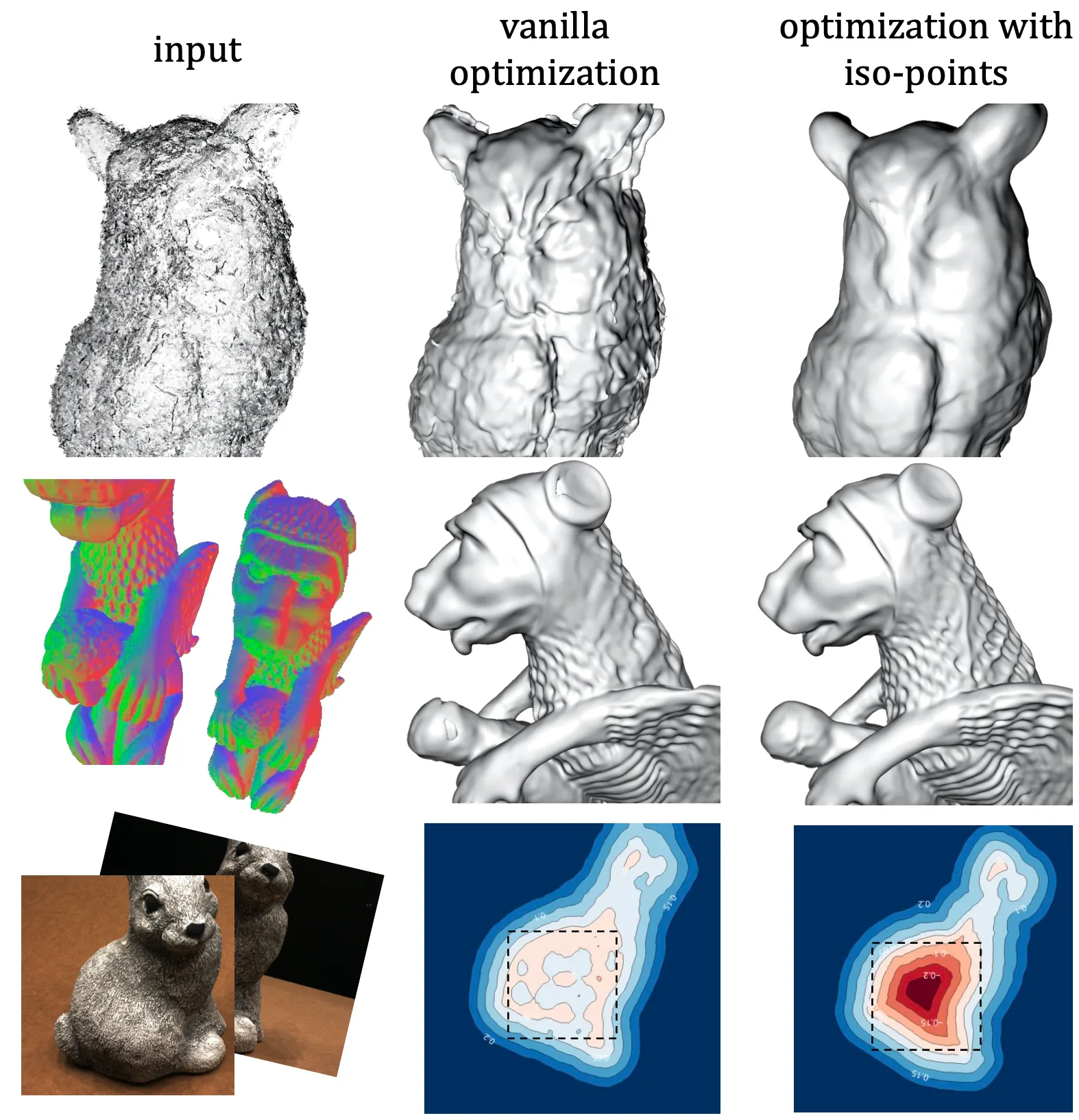
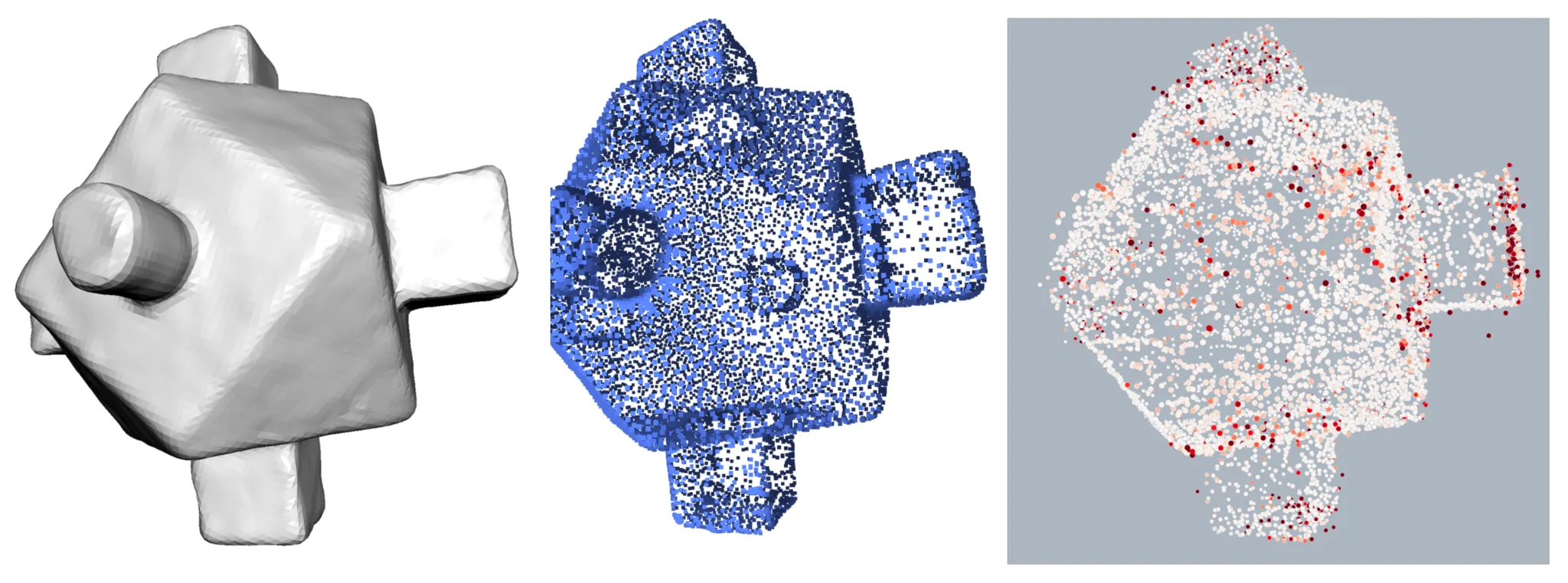
Surface Reconstruction
예시로, 위 그림의 첫 번째 행은 노이즈가 있는 Point Cloud 를 입력으로 하여 Implicit Surface 를 재구성한 것인데, 기존의 Vanilla Optimization 의 경우 outlier point 가 있는 부분부분마다 방울 형태의 언덕 구조나 양각들이 생성되는 것을 볼 수 있습니다.
위 그림의 두 번째 행은 Multi-View Image 를 입력으로 하여 Implicit Surface 를 재구성한 것인데 기존의 Vanilla Optimization 은 입력에 보이는 부분인 점 형태의 많은 음각과 같은 디테일한 기하학적 특성들을 재구성한 Implicit Surface 가 온전히 반영하지 못하는 모습을 볼 수 있습니다.
겉보기의 Implicit Surface 의 표현 자체에는 문제가 없더라도, 세 번째 행처럼 부적절한 입력 뷰가 들어올 경우에 Surface 내부의 Signed Distance 가 다시금 0 에 가까워진다던지의 topological noise 를 불러일으킬 수 있는 부작용이 있습니다.
이러한 문제점들을 해결하기 위해서, 논문에서는 학습 과정에서 네트워크가 산출하는 Neural Implicit Surface 로부터 Explicit 한 Iso-Points 들을 sampling 해 내고, 이를 최적화하는 방법론을 제시합니다. 그리고 기존의 Neural Implicit Surface 와 sampling 해낸 Iso-Points 를 합쳐서 3D 데이터를 표현하는 방법론을 Hybrid Nerual Surface Representation 이라고 명명합니다.

Method

논문에서는 그들의 방법론을 크게 다음과 같이 나누어 설명합니다.
1.
Implicit Surface 로 부터 Iso-Points 를 sampling 하는 방법
2.
Sampling 한 Iso-Points 를 optimization 에 활용하는 방법

Iso-Surface Sampling

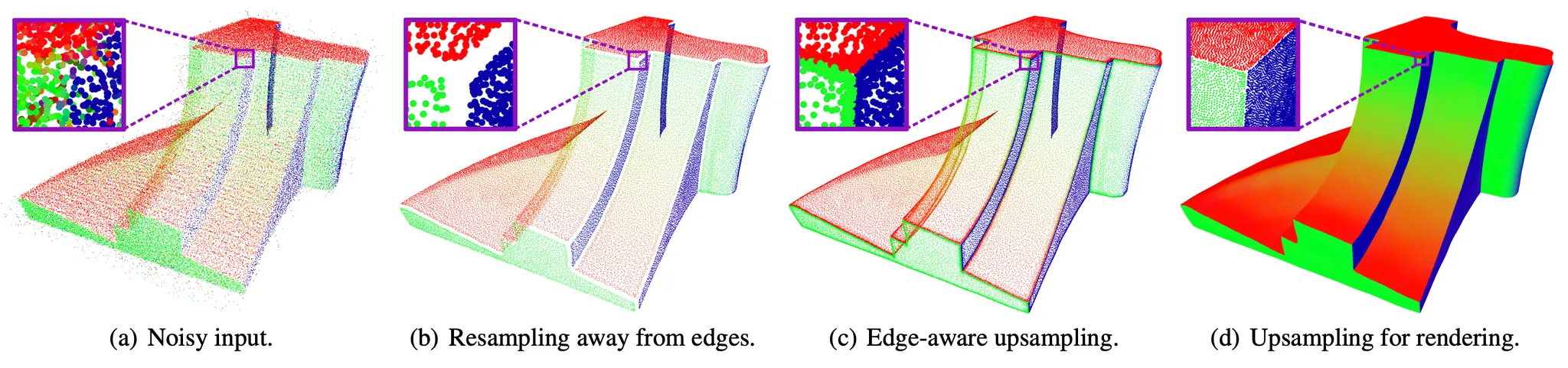
Implicit Surface 로 부터 Iso-Points 를 sampling 하는 방법은 또 다시 Projection, Resampling, Upsampling 의 3 개의 작은 단계들로 나누어집니다.
Iso-Surface Sampling
Projection 은 Initial Point Set 을 Implicit Surface 로부터 Zero-Level 에 놓여 있는 점들로 이동시켜 Surface 위에 올려놓는 단계이고, Resampling 은 Surface 에 올라간 점들이 너무 뭉쳐있거나, 너무 비어있지 않도록 조금씩 조정하는 단계이고, Upsampling 은 그렇게 어느정도 균일하게 Surface 위에 올라가진 점들 사이사이를 또다시 균일하게 채워넣어 밀도를 높이는 단계입니다.

Projection

논문에서 제시한 Projection 방법론은 Initial Point 들을 Implicit Surface 로 이동시키는 것이며, Newton’s Method 와 굉장히 흡사합니다. Newton’s Method 가 특정 지점에서 식의 해로 다가가기 위한 방법인 것과 유사하게, Implicit Function 의 값이 0 인 지점으로 다가가기 위해서 해당 지점에서의 gradient 의 음의 방향으로 조금씩 점을 이동시키는 방법을 사용한 것입니다. 초기 random sampling 된 qk∈Qtq_k \in Q_t 를 projection 하는 하나의 iteration 을 식으로 표현하면 다음과 같습니다.
qk+1=qk−JF(qk)+f(qk)q_{k+1} = q_k-J_F(q_k)^+f(q_k)
여기서 Jf+J_f^+ 는 Moore-Penrose pseudoinverse of the Jacobian 이라고 하는데, 다음과 같이 표현됩니다.
Jf+(qk)=JfT(qk)∣∣Jf(qk)∣∣2J_f^+(q_k)=\frac{J_f^T(q_k)}{\left|| J_f(q_k)|\right|^2}
여기서 JfJ_f 는 일반적인 3차원 공간에서의 함수 ff 의 Jacobian Matrix 이며, x,y,zx, y, z 에 따른 ff 의 편미분 값들로 구성되어 있기 때문에 backpropagation 과정에서 쉽게 얻어질 수 있습니다.
이렇게만 Projection 을 구성하면 곧장 ff 가 0 인 공간으로 projection 되어 Implicit Suface 위에 놓여 있는 Qt~\tilde {Q_t} 를 형성할 것 같지만, 실제로 sine activation function, positional encoding 등을 사용하는 현대의 많은 네트워크 설계들이 그들의 네트워크 parameter 에 따라서 산출하는 Signed Distance Function 의 변화가 상당히 복잡하고 gradient 가 부드럽지 않다고 합니다. 때문에 Netwon’s Method 를 직접적으로 가져다 사용하게 되면 쉽게 수렴점을 넘어서거나 진동하는 현상이 발생했고 논문에서는 이를 해결하기 위해서 단순한 clamping 을 도입합니다.
qk+1=qk−τ(JF(qk)+f(qk))q_{k+1} = q_k-\tau(J_F(q_k)^+f(q_k))
여기서 τ\tau 는 clamping 을 위한 함수로, 다음과 같이 표현됩니다.
τ(v)=v∣∣v∣∣min⁡(∣∣v∣∣,τ0)\tau(\rm{v})=\frac{\rm{v}}{\left||\rm{v}|\right|}\min(\left||\rm{v}|\right|, \tau_0)
위 식에서 τ0=D2∣Qt∣\tau_0=\frac{D}{2\left|Q_t \right|} 이며 DD 는 표현하려는 3D Model 의 형태를 감싸는 육면체 형태의 bounding box 의 diagonal length 입니다. 식에서 알 수 있듯이 한 번의 iteration 으로 발생하는 점의 이동거리를 τ0\tau_0 이상으로 허용하지 않겠다- 는 것이 보이실 것입니다.
앞서 초기에는 QtQ_t 가 random sampling 되었다- 라고 설명드렸었습니다.
크게 중요한 이야기는 아니지만, 논문에서 optimization 을 진행할 때 지속적으로 네트워크가 산출하는 Neural Implicit Surface 가 달라질텐데, 이 때마다 QtQ_t 는 모두 random sampling 을 하지는 않고, 이전 update 에서 산출된 Iso-Points Pt−1P_{t-1} 을 initial 로 하여 새로운 Projection 과정을 시작합니다. 이 내용이 전체적인 Implicit Surface Reconstruction 과정의 이해에 도움이 되실 것이라 믿습니다.

Uniform Resampling

Projection 과정을 통해 생성된 Base Iso-Points 인 Qt~\tilde {Q_t} 는 ff 가 0 인 지점으로 이동하라는 것 외에 딱히 제약조건이 걸려 있지 않았기 때문에 projection 된 점들이 뭉쳐있거나 구멍을 형성할 가능성이 충분합니다. Resampling 은 이렇게 Undersampling 되거나 Oversampling 된 영역이 생기는 것을 없애기 위해 높은 밀도를 가진 지역의 점들을 낮은 밀도를 가진 지역으로 점차 이동시키는 과정입니다.
논문에서는 이를 구현하기 위해 모든 점들을 그들 주변의 점들로부터 멀어지는 방향으로 이동시키는 방법을 사용합니다. 이를 수식으로 나타내면 다음과 같습니다.
q~←q~−αr\tilde{q} \larr \tilde{q} - \alpha r
여기서, α\alpha 는 상수이자 D/∣Qt~∣\sqrt{D/| \tilde{Q_t} |} 의 값을 가지며 rr 은 다음과 같이 표현됩니다.
r=∑qi~∈N(q~)w(qi~,q~)qi~−q~∣∣qi~−q~∣∣r = \sum_{\tilde{q_i}\in N(\tilde{q})} w(\tilde{q_i}, \tilde{q}) \frac {\tilde{q_i} - \tilde{q}} {\left|| \tilde{q_i} - \tilde{q} |\right|}
여기서 N(q~)N(\tilde{q}) 는 q~\tilde{q} 의 K-Nearest points 들을 의미하며, 정성적으로는 주변의 점들까지의 displacement 의 normalized weighted sum 의 반대방향으로 점을 이동함을 의미합니다.
이 때 사용한 weight ww 는 가까이 있는 주변의 점일수록 해당 점과 더 멀어지게 하기 위해서 가중치를 크게 주는 형태로 다음과 같이 설계합니다.
w(qi~,q~)=e−∥qi~−q~∥2σpw(\tilde{q_i}, \tilde{q})=e^{-\frac{\| \tilde{q_i}- \tilde{q} \|^2}{\sigma_p}}
마찬가지로 σp\sigma_p 는 상수이자 16D/∣Qt~∣16D/| \tilde{Q_t} | 의 값을 가집니다.
이와 같은 Resampling 과정을 통해 전체적으로 균일(Uniform) 하고 Surface 위에 있는 (Surface-Align) Point Set 을 얻을 수 있게 됩니다.

Upsampling

Iso-Surface Sampling 의 마지막 과정은 Upsampling 이며, 이 과정은 균일하고 Surface 위에 있는 점들의 전체적인 밀도를 증가시키는 과정입니다. 논문에서 사용한 방법론은 Huang et al. 의 Edge-Aware Resampling (이하 EAR) 과정에 기반합니다.
Edge-Aware Resampling
EAR 과 유사하게, 논문에서는 먼저 Resampling 과정으로 얻어낸 point 들의 normal 을 얻어냅니다. Jacobian 자체가 각 점들에 대한 Implicit Function 을 가장 급격하게 변화하는, gradient 방향을 알려주는 함수이기 때문에 이로부터 쉽게 얻어낼 수 있습니다. 이렇게 얻어낸 normal 정보를 바탕으로 Bilateral Normal Filtering 을 진행합니다.
Bilateral Normal Filtering? 일반적인 Bilateral Filtering 은 이미지 내에서 잡음을 제거 및 Smoothing 을 위해 사용하는 Gaussian Filtering 이 전체적인 이미지의 윤곽도 흐리게 하는 문제점을 해결하기 위해 사용되는 방법론입니다. 아무리 주변이라고 해도 픽셀 값의 차이가 크다면 필터링을 통해 새로 생성할 값을 만들 때 주변 픽셀들 중 해당 픽셀의 영향을 적게하여 윤곽을 뚜렷하게 하는 방법론입니다. Bilateral Normal Filtering 의 경우에는 잡음을 제거하고자 하는 것이 픽셀 값이 아니라 normal 값이라고 보시면 되는데, 다양한 방향을 가진 normal 을 smoothing 하되, 마찬가지로 윤곽을 의미하는 edge 영역의 구분을 어느정도 보존할 수 있는 방법론입니다.
Bilateral Normal Filtering 을 iterative 하게 진행하다 보면 point 영역 중에서 normal 이 급격하게 변화하는, 일명 edge 가 보이게 되는데 해당 부분의 normal 값들이 상당히 noisy 하기 때문에 EAR 에서는 이 영역의 점들을 아예 없애버립니다. 이것이 위 그림의 (b)(b) 과정입니다.
이렇게 사라져버린 edge 영역의 점들을 채워넣기 위해 논문에서는 EAR 에서 활용한 것보다는 간단한 형태의 point update 를 설계합니다. 이는 크게 edge 영역으로의 이동을 유발하는 attraction term 과 attraction term 이 과도하게 edge 로 point 들을 이동시키는 것을 억제하는 repulsion term 으로 이루어져 있습니다.
Δpattraction=∑pi∈N(p)ϕ(ni,pi−p)(p−pi)∑pi∈N(p)ϕ(ni,pi−p)Δprepulsion=0.5∑pi∈N(p)w(pi,q)(pi−p)∑pi∈N(p)w(pi,q)\begin{align*} &\Delta {\rm{p}_{attraction}}= \frac {\sum_{{\rm{p}}_i\in N({\rm{p}})}\phi({{\rm{n}}_i,{\rm{p}}_i-{\rm{p}})}({\rm{p}}-{\rm{p}}_i)}{\sum_{{\rm{p}}_i\in N({\rm{p}})}\phi({{\rm{n}}_i,{\rm{p}}_i-{\rm{p}})}}\\ &\Delta {\rm{p}_{repulsion}}= 0.5\frac {\sum_{{\rm{p}}_i\in N({\rm{p}})}w({{\rm{p}}_i,{\rm{q}})}({{\rm{p}}_i - {\rm{p}})}}{\sum_{{\rm{p}}_i\in N({\rm{p}})}w({{\rm{p}}_i,{\rm{q}})}} \end{align*}
p←p−τ(Δpattraction)−τ(Δprepulsion){\rm p} \larr {\rm p} - \tau(\Delta {\rm{p}_{attraction}}) - \tau(\Delta {\rm{p}_{repulsion}})
여기서 attraction term 에 사용된 ϕ\phi 는 ϕ(ni,pi−p)=e−(niT(p−pi))2σp\phi({{\rm{n}}_i,{\rm{p}}_i-{\rm{p}}}) = e^-{\frac{{\rm( n}_i^T({\rm p}-{\rm p}_i))^2}{\sigma_p}} 입니다.
Attraction term 을 먼저 살펴보면, ϕ\phi 라는 가중치 항목을 통해서 pp 에서 pip_i 로의 displacement 가 pip_i 의 normal 인 nin_i 와 이루는 각도가 작을수록 주변 점들 중 해당 pip_i 의 반대 방향으로의 가중치가 작고, 각도가 클수록 pip_i 의 반대 방향으로의 가중치가 큼을 알 수 있습니다. 정리하자면 각도가 클수록 pip_i 로부터 더 크게 멀어지려고 한다- 입니다. 그리고 이 각도는 plane 상의 점들 간에는 90°90\degree 이고 edge 부분에서 상대적으로 작아지게 되므로 주변 점들 중 동일한 plane 위의 점들과 상대적으로 크게 멀어지려고 하고, edge 에 가까워지려고 한다- 로 볼 수 있습니다.
Repulsion term 은 앞서 Resampling 단계에서 등장했던 식과 유사함을 보실 수 있습니다. ww 또한 동일한 함수이며 두 점이 가까울수록 ww 값 (가중치)이 커서 가까운 점일 수록 멀어지려고 한다- 로 볼 수 있습니다.
이 두 term 을 바탕으로 1. edge 주변에는 초기에 점이 비어있기 때문에 그 주변의 점들에 대해서는 attraction 및 repulsion term 모두로 인해서 점들이 채워지게 되고 2. 전체적으로는 repulsion term 을 통해 부가적으로 edge 의 채움을 통해 일부 구역의 넓어진 간격들에 맞게 전체적으로 점들을 퍼트리는 역할까지 하게 되는 것입니다.
이렇게 edge 부근의 비어있는 영역을 유의미하게 채워넣은 뒤, 전체적인 point 의 밀도를 올리기 위해서는 추가적으로 point 를 삽입하는 과정이 필요합니다. 논문에서는 이를 구현하기 위한 방법 또한 EAR 에서 차용하여 높은 곡률 (Curvature) 를 가지고 있거나 현재 밀도가 낮은 영역에 점을 iterative 하게 추가합니다.
높은 곡률을 가진 영역과 밀도가 낮은 영역 간의 trade-off 및 우선순위 조절은 논문에 언급되어 있지 않지만, EAR 을 제시한 논문에 따르면 다음과 같습니다.
P(p)=max⁡pi∈N(p)(2−nTni)ρC(p+pi2)P({\rm p})=\max_{{\rm p}_i \in N({\rm p})} (2-{\rm n}^T{\rm n}_i)^\rho C(\frac{{\rm p} + {\rm p_i}}{2})
여기서 CC 는 주어진 점이 특정 점 pp 의 주변 점들과 가지는 거리같은 개념으로, 얼마나 밀도가 낮은가를 판별하는 지표로 사용하는데, 다음과 같이 표현됩니다.
C(x)=D(x,p)=min⁡pi∈N(p)∥x−pi−niT(x−pi)ni∥C(x) = D(x, p) = \min_{{\rm p}_i \in N({\rm p})} \| x - {\rm p}_i -{\rm n}_i^T(x-{\rm p}_i){\rm n}_i \|
Euclidean Distance 와 다르게 이를 Orthogonal Distance 라고 부르는데, xx 로부터 pi{\rm p}_i 의 normal 에 내린 수선의 발의 길이라고 보시면 됩니다. 어느정도 눈치채셨겠지만, xx 에 p+pi2\frac{{\rm p} + {\rm p_i}}{2} 를 넣음으로써 특정한 점 p{\rm p} 를 기준으로 주변 점과의 중앙 점을 설정하여 해당 중앙 점이 주변 점과 가지는 orthogonal distance 들의 최솟값이 CC 가 되며 전반적으로 pp 가 그 주변 점들과 얼마나 떨어져 있는가를 나타내는 지표가 됩니다. 따라서, CC 값이 큰 p∗p^* 일수록 우선순위를 가질 가능성이 높습니다.
마찬가지로 (2−nTni)ρ(2-{\rm n}^T{\rm n}_i)^\rho 의 경우 normal 이 급격하게 변하는 구역의 점 p∗p^* 이 normal 사이의 각도가 상대적으로 크기 때문에 큰 (2−nTni)(2-{\rm n}^T{\rm n}_i) 값을 가지고 우선순위를 가질 가능성이 높습니다.
위의 두 가지 요소 때문에 밀도가 낮은 구역의 점일수록, normal 이 급격하게 변하는 edge 구역의 점일수록 우선순위가 높게 점이 선택되며, 이 둘 사이의 비중은 edge-sensitiviy parameter 인 ρ\rho 값으로 조절할 수 있게 됩니다. EAR 에서는 이렇게 선택된 점 p∗p^* 에 대해서 P(p∗)P(p^*) 을 최대화하는 pip_i 를 pi∗∗p_{i^*}^* 라고 할 때 p∗p^* 와 pi∗∗p_{i^*}^* 의 중앙 지점에 새로운 점을 놓았는데, 논문에서는 중복된 점을 막는다는 이유로 13(pi∗∗+2p∗)\frac{1}{3}(p_{i^*}^* + 2p^*) 에 놓았다고 합니다.

Utilizing iso-points in optimization

지금까지 논문에서는 Neural Implicit Surface 로 부터 Iso-Points 를 sampling 하는 과정에 대해서 설명했습니다. 논문에서는 이어서 그들이 생성해낸 Iso-Points 가 optimization 과정에서 어떻게 활용할 수 있는지를 크게 두 가지로 나누어서 설명합니다.

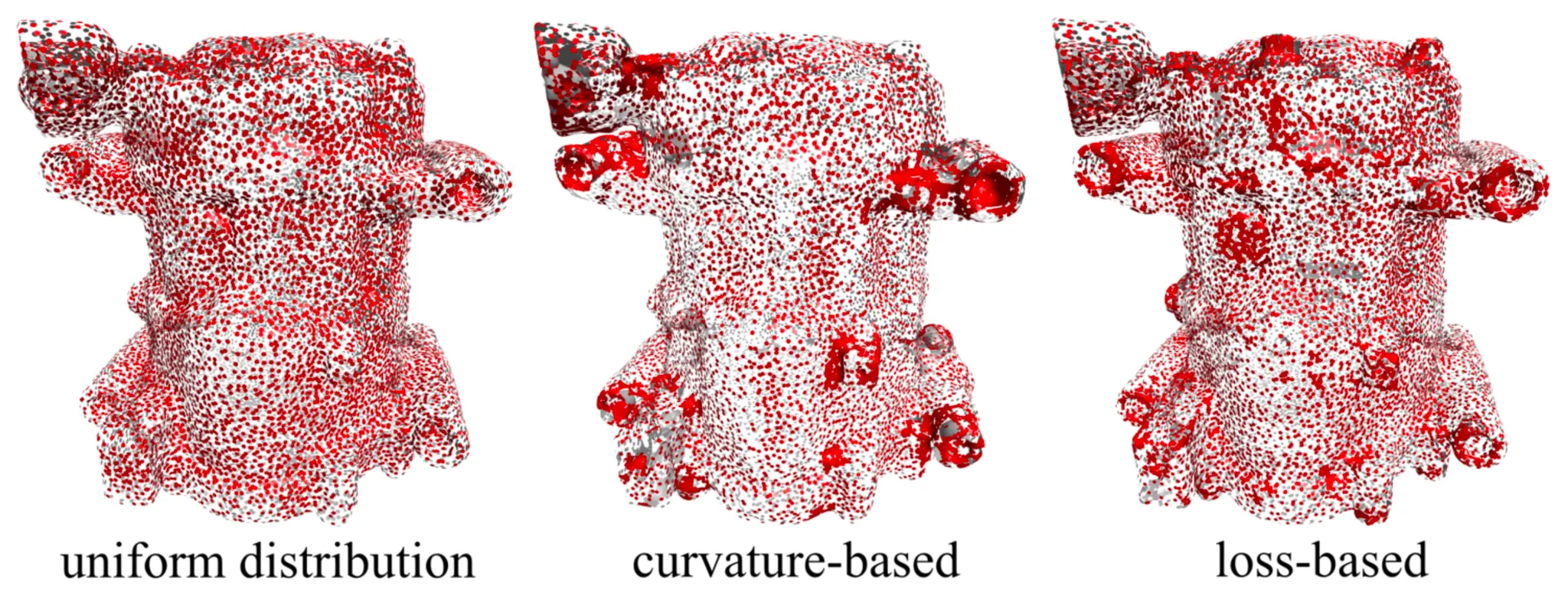
Iso-Points for Importance Sampling

Multi-View Image 나 Noisy Point Cloud 만을 입력으로 하여 Neural Implicit Fuction 을 최적화할 수는 있지만 고해상도의 3D Model 을 표현하기 위해서는 필연적으로 Implicit Surface 와 근접한 영역에서 sampling 된 supervision points 들과 같은 풍부한 학습 데이터가 필요합니다.
하지만, 이러한 3D supervision 의 풀은 현저하게 적기 때문에, 기하학적인 디테일을 챙기기 위해 Supervision Point 들을 학습 과정에서 활용하기 어려웠고 이를 학습의 중간에 만들어내는 것 또한 해당 분야의 과제로 남아있었습니다.
Importance Sampling
이러한 상황에서 논문의 Iso-Points 는 Nerual Implicit Function 을 최적화하는 학습과정 중간에 추가적인 기하학적인 정보를 제공할 수 있다고 합니다. 가장 대표적인 예시로 Saliency Metric 을 설정하여 구조 속에서 돌출된 부분을 찾아내어 추가적인 sample 을 놓는 방법으로 활용할 수 있다고 합니다. 논문에서는 크게 curvature-based, loss-based metric 을 소개합니다.
Curvature-based Saliency Metric 은 각각의 점들에 대해서 Laplacian 의 norm 형태로 근사할 수 있으며, 다음과 같이 계산됩니다.
Rcurvature(p)=∥p−∑pi∈N(p)pi∥{\mathcal{R}}_{{\rm curvature}}({\rm p}) = \|{\rm p}-\sum_{{\rm p}_i \in N({\rm p})}{\rm p}_i \|
특정 점 p{\rm p} 에 대해서 그 주변 점들의 평균 점과의 거리로 정의되며, 평탄하지 않은 지역에서의 값이 일반적으로 클 것이라는 느낌이 드실 겁니다.
Loss-based Saliecy Metric 은 각각의 점들에 대해서 다음과 같이 계산됩니다.
Rloss(p)=1N∑iNloss(p){\mathcal{R}}_{{\rm loss}}({\rm p}) = \frac{1}{N} \sum_i^N {\rm loss(p)}
이는 Multi-View Reconstruction 에서 특정 점 p{\rm p} 에 대해서 해당 점이 포함된 렌더링 뷰와 그에 해당하는 Ground Truth 가 가지는 loss 들의 평균치입니다. 돌출 구조를 파악하여 sample 을 뿌려주겠다- 라기 보다는 loss 가 커서 잘 예측하고 있지 못한 곳에 sample 을 뿌려주겠다- 이며, 이를 일반적으로 Hard Example Mining 이라고 표현합니다.
이렇게 찾은, Saliency Metric 이 높은 점들의 집합을 T∗={t∗}{\mathcal{T}^*} = \{t^*\} 이라고 할 때, 새로운 sample 들은 해당 t∗t^* 과 의 거리가 설정한 threshold σ\sigma 보다 작은 점들 pi{\rm p}_i 에 대해서 그 주변 점들과의 1:21:2 거리를 가지는 위치에 놓게 됩니다. 이를 수식으로 표현하면 다음과 같습니다.
pnew,i=23p+13pi, ∀pi∈N(p), ifmin⁡t∗∥p−t∗∥≤σ{\rm p}_{\rm new, i}=\frac{2}{3}{\rm p} + \frac{1}{3}{\rm p}_i,\ \forall{\rm p}_i \in N({\rm p}),\ {\rm if} \min_{t^*} \| {\rm p} - t^* \| \le \sigma

Iso-Points for Regularization

논문에서는 Implicit Surface 에서 얻어낼 수 있는 Explicit Represenation 인 Iso-Points 가 optimization 과정에서 기하학적 prior 로 사용될 수 있다고 제안합니다.
Progression of Overfitting
특히, Noisy 한 Point Cloud 에 fitting 하는 Neural Implicit Surface 를 optimization 할 때 위 그림과 같이 학습의 초기 단에는 부드러운 표면을 재구성하지만, 학습이 진행됨에 따라 구체적이고 디테일한 구조 (보통 High Frequency Signal 이라는 표현을 사용합니다.) 들을 반영하게 되면서 쉽게 overfitting 되는 경향이 있습니다.
이러한 점을 해결하기 위해서 기존에는 학습을 일찍 중단하거나 (Early Stopping), 시간이 지남에 따라 0 에 가까운 weight 들을 많이 만들어 네트워크의 표현력을 낮추거나 (Weight Decay), 학습 단계에서 동적으로 네트워크의 연결을 끊어 복잡도를 낮추는 (Drop Out) 방법들을 사용했지만, 이러한 방법론은 어떤 하나의 optimization 과정에 초점을 맞춘 방법이라기 보다는 일반적인 방법론으로 모든 곳에서 사용 가능한 방법입니다.
논문에서는 이러한 일반적인 방법론에서 벗어나 Iso-Points 를 레퍼런스로 사용하게 될 Point Cloud 의 일관되고, 부드러우면서, 어느정도 동적 변경이 가능한 범위 내의 근사 표현으로 취급하여 optimization 에 도움을 줄 수 있다고 제안했습니다. Iso-Points 의 일관성과 부드러움은 optimization 이 노이즈에 크게 변동되거나 overfitting 되지 않도록 유도할 수 있으며, 동적 근사 표현이라는 점은 일관되게 구체적인 기하학적인 디테일에 대한 정보를 네트워크에게 줄 수 있었다고 합니다.
실제로 논문에서는 300 iteration 동안 학습하여 어느정도의 Neural Implicit Surface 가 구성된 후 Iso-Points 를 생성하고 Iso-Points 로 부터 얻은 정보들로 optimization 을 강화하고, 다시 1000 iteration 마다 Iso-Points 를 업데이트하는 형태를 사용하여 부드러우면서도 디테일을 가진 구조를 학습했다고 합니다.
앞서는 Iso-Points 들이 optimization 에서 어떻게 활용되는지에 대한 대략적인 설명이었습니다. 구체적으로 논문에서 optimization 에 다음의 세 가지 방법들을 사용합니다.
첫 번째로, 논문에서는 Iso-Points 를 데이터 희소성을 극복하기 위한 추가적인 학습 데이터로 활용합니다. 구멍이 뚫려있는 것과 같이 일부 구역이 sparse 한 레퍼런스 Point Cloud 를 가지고 있는 경우에는 해당 부분 근처에서 Neural Implicit Function 을 학습하기 어렵습니다. 하지만, Iso-Points 는 그 생성 과정 자체에서 uniformity 를 보장받기 때문에 해당 데이터를 활용하여 optimization 을 보정해 줄 수 있습니다. 이는 다음과 같은 loss 항목으로 조절할 수 있습니다.
LisoSDF=1∣P∣∑p∈P∣f(p)∣{\mathcal L}_{\rm isoSDF} = \frac{1}{|{\mathcal P}|}\sum_{{\rm p}\in {\mathcal P}}|f({\rm p})|
Iso-Points 가 있는 좌표의 ff 값을 0 으로 학습하게끔 유도하여, 구멍이 뚫려 점이 없는 지역도 Iso-Points 의 점들로 인해 자연스러운 Neural Implicit Surface 를 형성하는 Implicit Function 을 학습할 수 있게끔 하는 것입니다.
두 번째로, 논문에서는 기하학적인 제약조건을 추가하여 자연스러운 Implicit Function 을 학습하기 위해 Iso-Points 를 활용합니다. 각 point 의 normal 은 학습한 Implicit Function 의 Jacobian 으로부터 얻을 수 있지만, 특정 점 및 그 근처의 점들 집합에 PCA 를 활용하여 근사치를 구해낼 수도 있습니다. Iso-Points 가 보여주는 분포에서 PCA 를 통해 얻어낸 normal 과 학습한 Implicit Function 의 Jacobian 을 통해 구해낸 normal 이 일치하도록 학습에 조건을 추가함으로써 Iso-Points 가 가지고 있던 표면의 smoothness 를 학습에 반영할 수 있는 것입니다. 이러한 조건은 loss 항목을 통해 추가할 수 있습니다.
LisoNormal=1∣P∣∑p∈P(1−∣cos⁡(JfT(p),nPCA)∣){\mathcal L}_{\rm isoNormal} = \frac{1}{|{\mathcal P}|}\sum_{{\rm p}\in {\mathcal P}}(1-|\cos(J_f^T({\rm p}), {\rm n}_{{\rm PCA}})|)
위 식의 cos⁡\cos 는 벡터간 코사인 유사도를 의미하며, loss 값이 작아지려면 Jacobian 을 통해 얻어낸 normal 과 PCA 를 통해 얻어낸 normal 이 유사해야 함을 알 수 있습니다.
마지막으로, 논문에서는 noisy 한 레퍼런스 Point Cloud 에서 outlier 를 제거하는데 Iso-Points 를 활용합니다. 이는 레퍼런스 Point Cloud 에 속하는 각각의 점 q{\rm q} 에 대해서 다음과 같은 bilateral weight 값을 구하고, 해당 값이 큰 점들을 outlier 로 선정하는 방식입니다.
v(q)=min⁡p∈Pϕ(np,p−q)ψ(np,nq)ψ(np,nq)=e−(1−1−npTnq1−cos⁡(σn))2v({\rm q})=\min_{{\rm p}\in{\mathcal P}}\phi({\rm n}_{\rm p}, {\rm p}-{\rm q})\psi({\rm n}_{\rm p}, {\rm n}_{\rm q})\\ \psi({\rm n}_{\rm p}, {\rm n}_{\rm q})=e^{-(1-\frac{1-{\rm n}_{\rm p}^T{\rm n}_{\rm q}}{1-\cos(\sigma_n)})^2}
Iso-Points for Regularization (Right: Red Point Outlier)
여기서 P{\mathcal P} 는 Iso-Points 들의 집합, σn\sigma_n 은 normal difference 에 대한 sensitivity factor 라고 보시면 되며, 정성적으로 해석하면 가장 가까운 점의 거리가 생각보다 멀거나, 그렇지 않다면 가까운 점들과 가지는 normal 방향이 차이가 크거나, 그렇지도 않다면 가까운 점들과 normal 방향으로의 displacement 를 가지거나 하는 점들을 outlier 라고 볼 가능성이 크다- 정도로 이해하시면 될 것 같습니다.

Results

논문에서는 그들이 설계한 Iso-Points 는 기존의 optimization 과정에 단순히 추가하여 활용하는 것만으로도 좋은 퀄리티의 Implicit Function 을 학습할 수 있다는 것을 보여주기 이해서 SOTA 방법론들에 Iso-Points 를 추가하여 기존의 방법론을 정량적 및 정성적으로 개선할 수 있었다는 것을 보여줍니다.

Sampling with Iso-Points

먼저, 논문에서는 Multi-View Reconstruction 문제에서 Training Sample 을 만들기 위해서 Iso-Points 활용하는 것의 이점을 보여주기 위해 baseline 으로 SOTA Neural Implicit Renderer 인 IDR 을 가져옵니다. 이는 앞서 언급했듯이 Multi-View Reconstruction 에서 디테일한 기하학적 구조를 포함한 고해상도의 3D Model 을 재구성하기 위해서는 필요한 과정입니다.
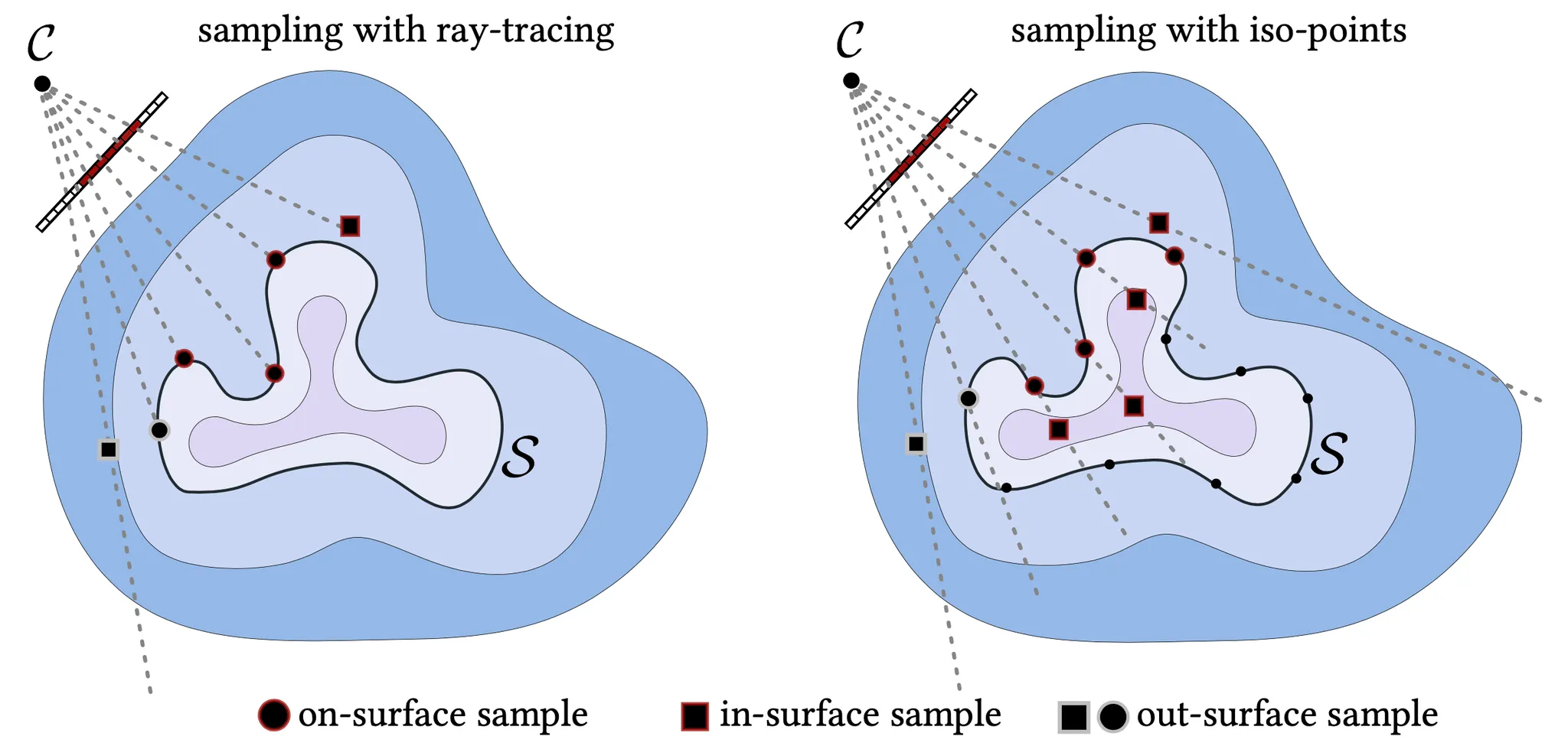
2D Illustration of Two Sampling Strategies
위 그림의 좌측은 IDR 의 Sampling Strategy 를, 우측은 Iso-Points 를 사용하여 IDR 의 Sampling Strategy 를 변경한 것입니다.
기존의 IDR 의 Sampling Strategy 는 관측 위치와 이미지의 각 픽셀로부터 이어지는 Ray 를 그어 그 위에서 물체의 Surface 위에 놓여 있는 On-Surface Sample, 물체의 안에 놓여 있는 In-Surface Sample, 물체의 밖에 놓여 있는 Out-Surface Sample 구분 되는 Sample 을 지정해내는 방법론입니다.
이 때 IDR 에서는 이미지 상에서 물체 내부를 지나면서 Suface 랑 만나는 점들을 On-Surface Sample 로 지정하고, 이미지 상에서 물체 내부를 지나지만 Surface 랑 만나지 않는 ray 위의 점들 중에서 In-Surface Sample 로 지정하고, 이미지 상에서 물체 외부를 지나지만 Surface 랑 만나거나 가장 낮은 Signed Distance 를 가지는 점들 중에서 Out-Surface Sample 을 지정했습니다.
하지만 논문에서 제시한 방법론에서는 Iso-Points 를 도입하여 Iso-Points 자체를 On-Surface Sample 의 후보로 지정하고, 이들 중 projection 이 이미지 상에서 물체 내부에 있는 것들을 On-Surface Sample 로 지정하게 됩니다. In-Surface Sample 은 이렇게 지정한 On-Surface Sample 과 이어지는 Ray 상에서 Signed Distance 가 가장 낮은 점으로 지정했고, Out-Surface Sample 은 이미지 상에서 물체 외부를 지나는 Ray 위의 가장 낮은 Signed Distance 를 가지는 점들로 지정했습니다.

Surface details from importance sampling

위에서 기술한 방식의 Training Sample 지정이 얼마나 효과 있는지를 보여주기 위해 논문에서는 아래와 같은 자료를 제시합니다.
Quantitative Results of Sampling with Iso-Points
위는 Sketchfab dataset 으로 구성된 Point Cloud 와 Multi-View Reconstruction 으로 구성한 Point Cloud 의 2-way Chamfer Distance 를 측정한 것입니다. 이 때 가장 가까운 점과의 normal cosine similarity 를 기반으로 한 Normal Chamfer Distance 또한 측정했고, base line 에 비해서 현저하게 개선된 모습을 볼 수 있었습니다. 더불어 Importance Sampling 의 효과 또한 입증할 수 있었습니다.
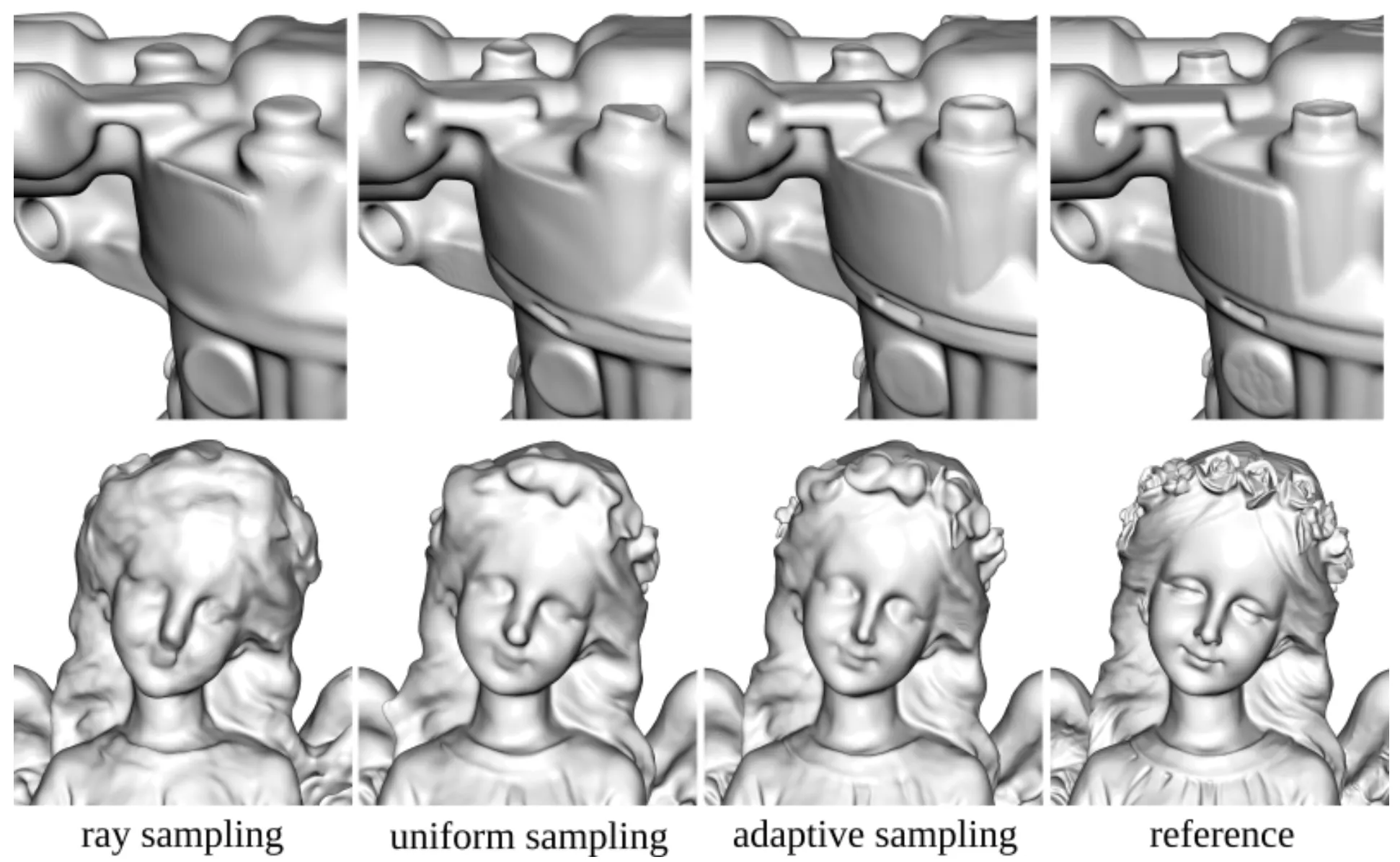
Qualitative Results of Sampling with Iso-Points
위는 Sketchfab dataset 의 COMPRESSOR 와 ANGEL2 에 대해서 Multi-View Reconstruction 을 진행했을 때 Sampling Strategy 에 따라 나타난 정성적인 결과를 보여줍니다. Iso-Points 를 사용한 결과가 레퍼런스와 더 유사한 것을 볼 수 있었으며, loss-based Importance Sampling 에서 디테일한 기하학적인 구조들이 잘 드러나는 것을 확인할 수 있었습니다.

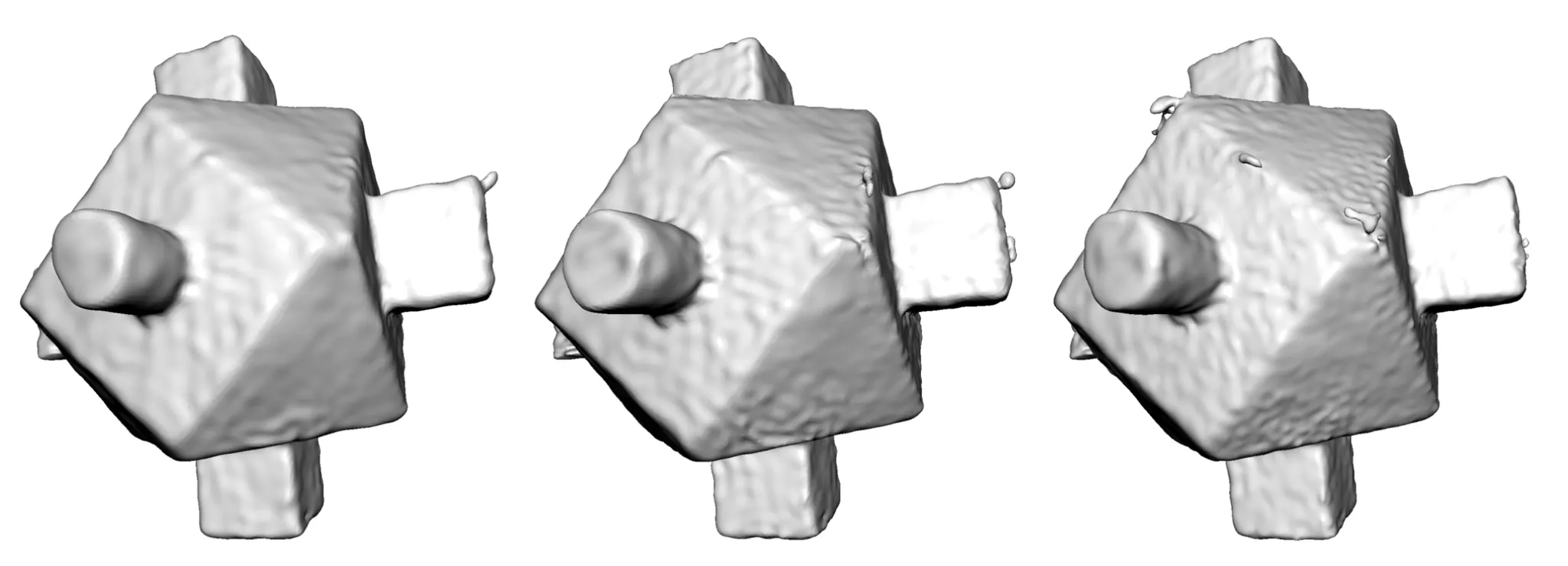
Topological correctness from 3D prior

IDR 의 Multi-View Reconstruction 은 DTU dataset 에 대해서 구체적인 기하학적인 디테일을 포함할 수 있었지만, 그들이 재구성한 surface 는 visible 한 영역 안쪽에 tological 한 오류가 많았습니다. 반면, IDR 과 다르게 논문에서는 Iso-Points 를 사용하는 것이 이러한 topological accuracy 를 높일 수 있음을 보여줍니다.
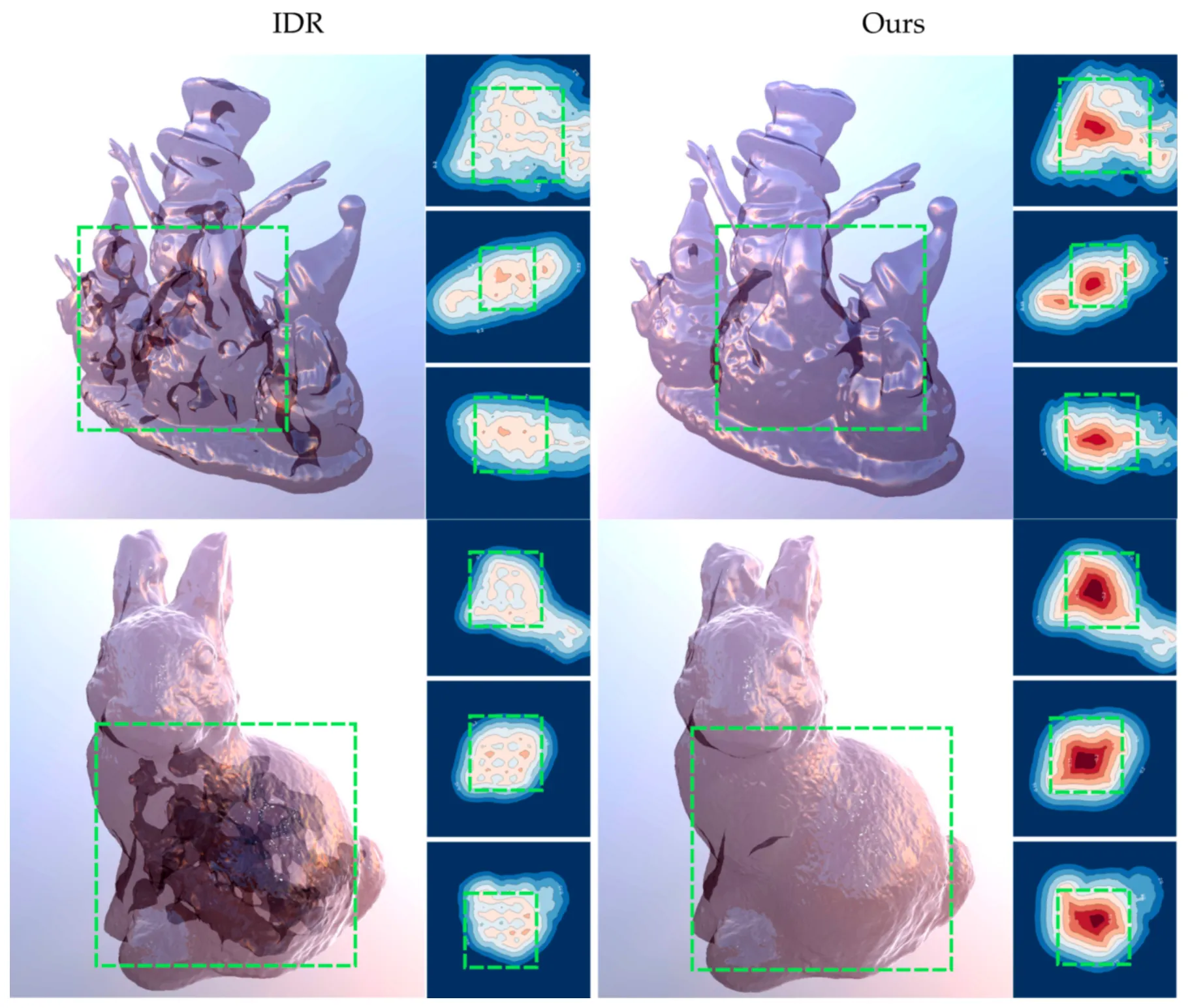
Topological Correctness
위 그림이 IDR 과 논문의 방법론으로 재구성한 Surface 에 대한 위상을 나타내줍니다. 내부가 잘 드러나도록 Physically-based Renderer 를 사용하여 물체의 구성을 투명하고 광택이 있는 물질로 바꾸어서 렌더링한 결과로, 논문의 Iso-Points 를 활용한 Multi-View Reconstruction 은 Signed Distacne 가 안쪽으로 갈 수록 균일하게 감소하는 현상이 보였지만 IDR 은 그렇지 않았습니다. 실제로 IDR 은 겉보기에도 렌더링된 이미지 상에서 검은 영역이 보였고, 이는 Surface 내부 구조물 때문에 빛의 투과에 영향을 미쳤기 때문입니다.

Regularization with Iso-Points

논문에서는 Iso-Points 를 Regularization 에 사용하는 경우에 얻어지는 이점에 대해서 평가하기 위해서 noisy 한 Point Cloud 로부터의 Surface Reconstruction 에 대해 실험합니다. 비교의 대상이 될 baseline 으로는 오픈소스로 공개되어 있는 SIREN 의 코드베이스를 사용했으며, noisy 한 Point Cloud 는 Artec Eva 라는 3D scanner 를 사용했다고 합니다.
이 때, 일반적인 SIREN 의 코드베이스는 다음과 같은 objective 로 학습이 진행됩니다.
L=γonSDFLonSDF+γnormalLnormal+γoffSDFLoffSDF+γeikonalLeikonal{\mathcal L}= {\gamma_{\rm onSDF}}{\mathcal L}_{\rm onSDF} + {\gamma_{\rm normal}}{\mathcal L}_{\rm normal} + {\gamma_{\rm offSDF}}{\mathcal L}_{\rm offSDF} + {\gamma_{\rm eikonal}}{\mathcal L}_{\rm eikonal}
여기서 각각의 loss term 은 아래와 같이 정의됩니다.
LonSDF=∑qs∈Qs∥f(qs)∥∣Qs∣, Lnormal=∑qs∈Qs∣1−cos⁡(JfT(qs),ns)∣∣Qs∣LoffSDF=∑qo∈Qoe−α∣f(qo)∣∣Qo∣, Leikonal=∑q∈Qo∪Qs∣1−∥JfT(q)∥∣∣Qs∣+∣Po∣\begin{align*} &{\mathcal L}_{\rm onSDF} = \frac{\sum_{q_s\in Q_s}\| f(q_s)\|}{|Q_s|},\ {\mathcal L}_{\rm normal} = \frac{\sum_{q_s\in Q_s}|1-\cos(J_f^T(q_s),n_s)|}{|Q_s|}\\ &{\mathcal L}_{\rm offSDF} = \frac{\sum_{q_o\in Q_o}e^{-\alpha|f(q_o)|}}{|Q_o|},\ {\mathcal L}_{\rm eikonal} = \frac{\sum_{q\in Q_o \cup Q_s}|1-\|J_f^T(q)\||}{|Q_s| + |P_o|}\\ \end{align*}
간략히만 해당 loss 에 대해서 설명을 드리자면,
1.
LonSDF{\mathcal L}_{\rm onSDF} 은 레퍼런스 Point Cloud 에서 sampling 된 Surface 에 놓여 있는 점들은 ff 값이 0 으로 가게끔 유도하는 loss 입니다.
2.
LoffSDF{\mathcal L}_{\rm offSDF} 는 bounding cube 에서 sampling 된 Surface 이에 없는 점들은 ff 값이 0 으로 가지 않게끔 유도하는 loss 입니다.
3.
Lnormal{\mathcal L}_{\rm normal} 은 학습한 ff 의 Jacobian 을 통해 얻어낸 normal 과 레퍼런스 Point Cloud 에서 sampling 된 Surface 위에 놓여 있는 점들의 normal 이 align 되기를 유도하는 loss 입니다.
4.
Leikonal{\mathcal L}_{\rm eikonal} 은 Jacobian 의 norm 이 1 을 유지하도록 constraint 를 주는 loss 입니다.
여기서 Iso-Points 의 결과를 실험하기 위해서 앞서 설명드렸던 LisoSDF{\mathcal L}_{\rm isoSDF} 와 LisoNormal{\mathcal L}_{\rm isoNormal} 를 추가하게 됩니다. 여기까지의 objective 의 변화는 다음과 같습니다.
L=γonSDF(LonSDF+LisoSDF)+γnormal(Lnormal+LisoNormal)+γoffSDFLoffSDF+γeikonalLeikonal{\mathcal L}= {\gamma_{\rm onSDF}}({\mathcal L}_{\rm onSDF} + {\mathcal L}_{\rm isoSDF}) + {\gamma_{\rm normal}}({\mathcal L}_{\rm normal}+ {\mathcal L}_{\rm isoNormal}) +\\ {\gamma_{\rm offSDF}}{\mathcal L}_{\rm offSDF} + {\gamma_{\rm eikonal}}{\mathcal L}_{\rm eikonal}
여기서 앞서 Method 에서 언급했던 Outlier-Aware loss 를 추가하면 다음과 같은 항목의 변화가 생깁니다.
LonSDF=∑qs∈Qsv(qs)∥f(qs)∥∣Qs∣Lnormal=∑qs∈Qsv(qs)∣1−cos⁡(JfT(qs),ns)∣∣Qs∣\begin{align*} &{\mathcal L}_{\rm onSDF} = \frac{\sum_{q_s\in Q_s}v(q_s)\| f(q_s)\|}{|Q_s|}\\ &{\mathcal L}_{\rm normal} = \frac{\sum_{q_s\in Q_s}v(q_s)|1-\cos(J_f^T(q_s),n_s)|}{|Q_s|} \end{align*}
Outlier 들에 적은 가중치를 주어 이들이 최종적인 loss 에 기여하는 정도를 줄이는 형태가 되는 것으로 이해하시면 됩니다.
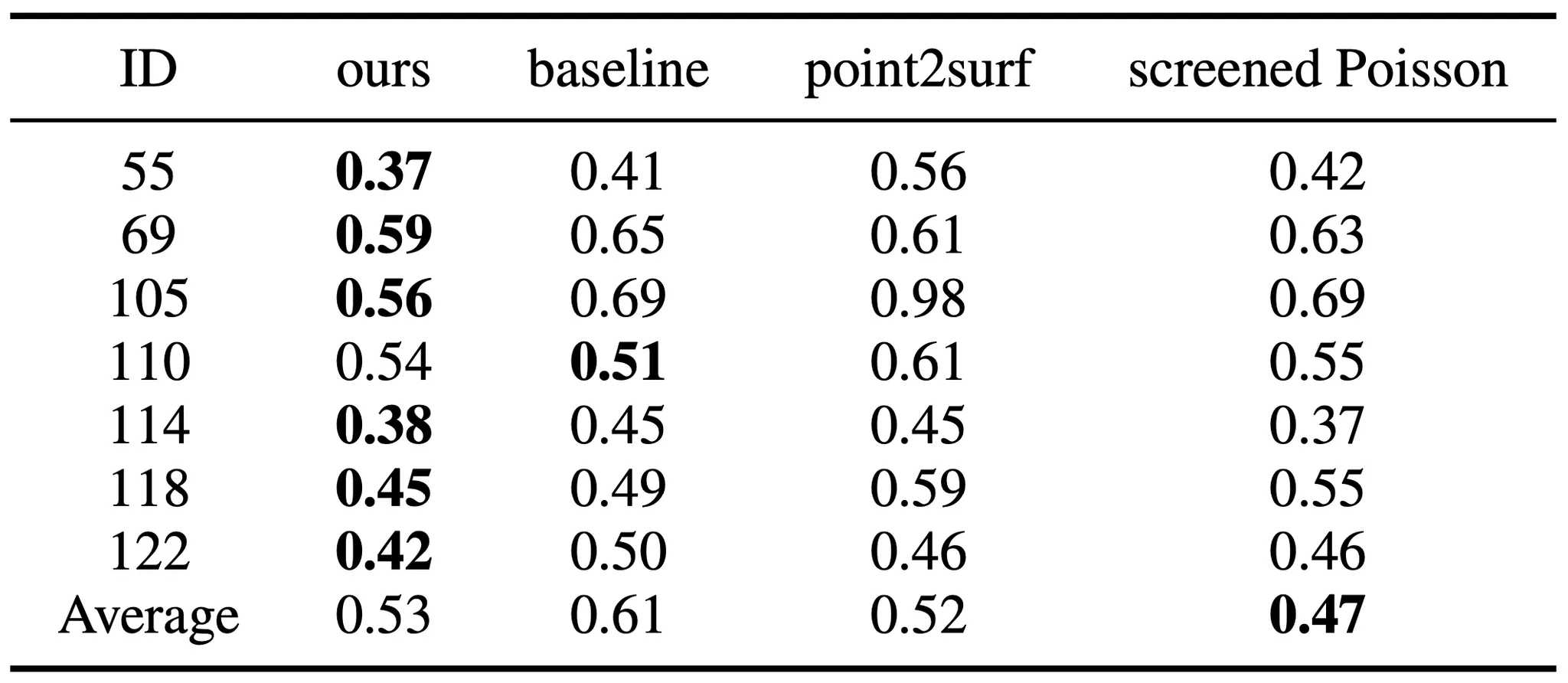
이렇게 설계된 Iso-Points 를 사용한 Regularization 을 정량적으로 평가한 내용은 아래와 같습니다. 평가 지표로 사용한 것은 L1 Chamfer Distance 입니다.
Quantitative Results of Surface Reconstruction
Point2Surf 는 local Poisson equation 을 풂으로써 표면에 잘 align 된 reconstuction 을 진행한 방법론이고, screened Poisson 은 unoriented point set 을 Implicit Neural Function 에 fitting 한 방법론입니다. 두 방법론 모두 Surface Reconstruction 에 초점을 맞춘 논문들이며 논문에서는 baseline 과 더불어 이들 둘과 함께 논문의 방법론을 평가합니다. Baseline 및 다른 두 구현체들과 비교했을 때 Iso-Points 를 활용하는 논문의 Surface Reconstruction 이 Ground Truth 와의 Chamfer Distance 가 확연히 작은 것을 볼 수 있었습니다.
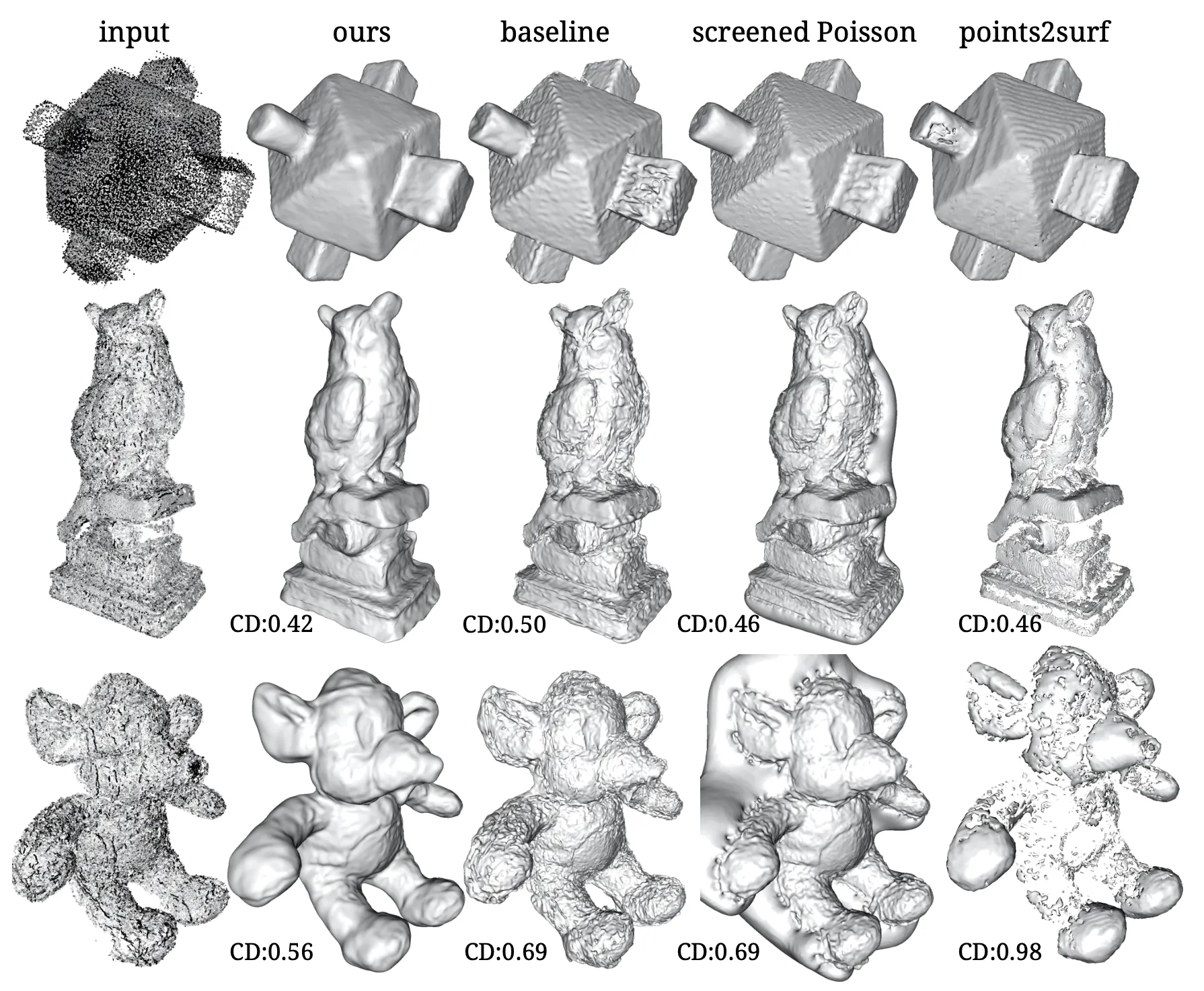
Implicit Surface Reconstruction from Noisy and Sparse Point Cloud
위 그림은 논문의 방법론 및 비교 대상들의 Reconstruction 결과에 대한 정성적인 비교를 나타냅니다. 논문의 방법론이 확실히 baseline 이나 screened Poisson 에 비해서 noise 를 잘 줄여주는 것을 볼 수 있었고, Point2Surf 는 noisy 한 input 을 잘 핸들링하는 모습을 보였지만 Point Distribution 자체에 민감한 sign propagation 을 사용하여 mesh 사이사이에 구멍이 보이는 것을 확인할 수 있었습니다.

Performance Analysis

논문의 Iso-Points 에서 주요하게 고려할 수 있는 문제점은 Iso-Points 를 생성하는데 추가적인 리소스가 들어간다는 점입니다. 평균적으로 한 번의 Iso-Points 를 생성하는데는 4번의 Newton’s Method iteration 이 필요했고 이는 training iteration 을 3 번 수행하는 것과 비슷한 시간이라고 합니다. 더불어, Iso-Points 를 매 학습 iteration 마다 생성하는 것이 아니라 주기적으로 생성하기 때문에 (ex. 1000 iteration 마다) 전체 학습 과정에서 Iso-Points 의 생성이 차지하는 시간적인 비중은 그렇게 크지 않다고 합니다.
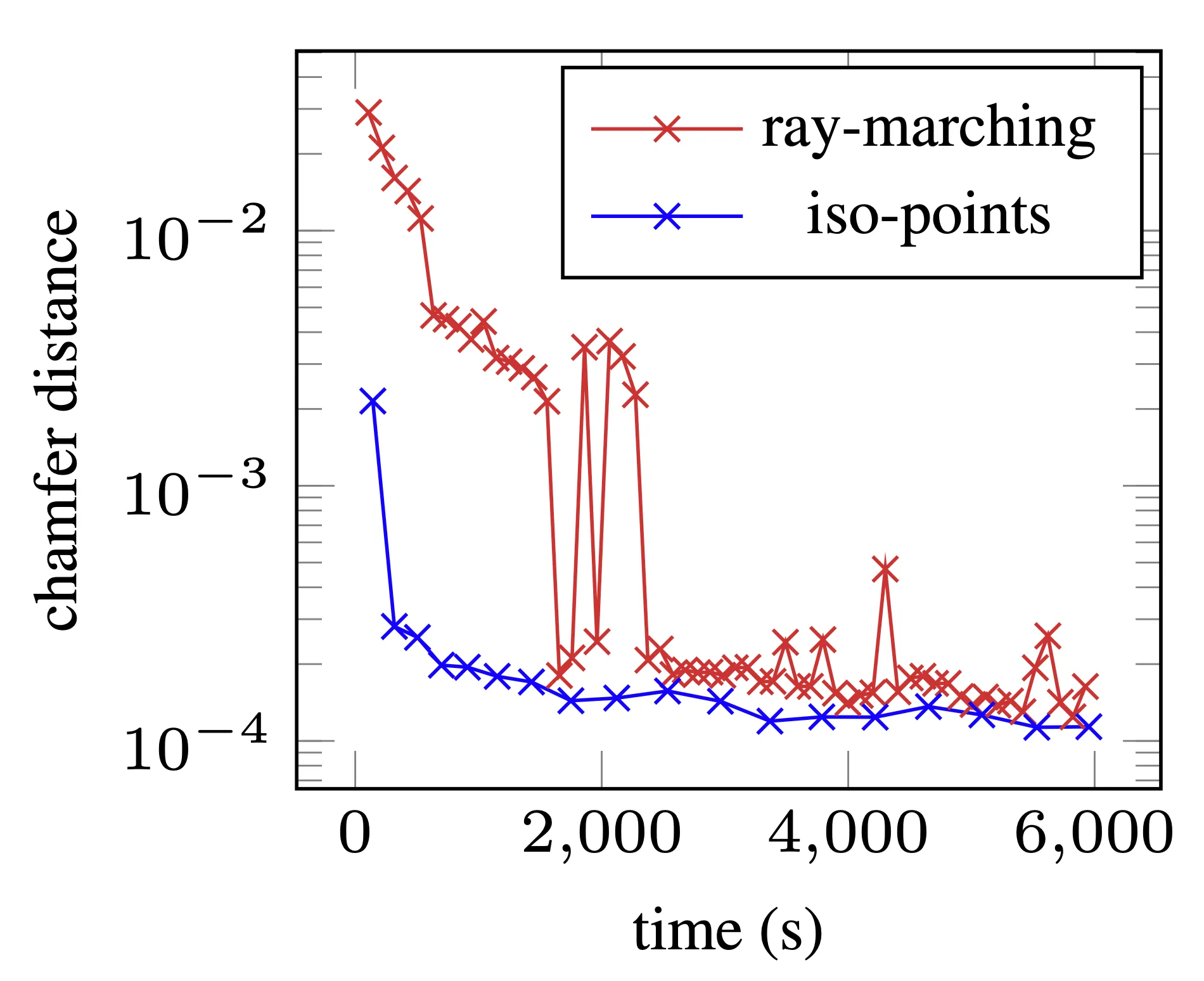
Validation Error VS Optimization Time
위 그래프는 Optimization Time 과 Quality 간의 그래프입니다. 논문에서 제시한 그래프에 따르면 극단적으로 생각해 보아도 모든 time stamp 에서 성능이 좋으면 사용하지 않을 이유가 없습니다.

Conclusion

이것으로 논문 “Iso-Points: Optimizing Neural Implicit Surfaces with Hybrid Representations” 의 내용을 간단하게 요약해보았습니다.
Implicit 과 Explicit 을 모두 사용하는, Hybrid Representation 이라는 점에서 이목이 끌렸던 논문인데, 생각보다 알아야 할 내용이 많고 그 깊이도 깊어서 어느정도 배경지식이 있다고 자부하고 있었는데도 읽는데 어려움을 꽤 겪었던 것 같습니다.
3D Vision 분야에서 읽었던 논문은 여태까지 거의 응용 쪽에 가까웠는데 그래도 어느정도 범용적으로 사용될 수 있을만한 방법론을 제시해준 논문이어서 흥미롭게 읽을 수 있었던 것 같습니다. 관련 분야를 공부하시는 분들께는 한 번 추천해볼만 한 논문이라고 느꼈습니다.