Sinusoids
•
가장 간단한 소리의 형태: sine wave
•
원 위의 점이 등속도로 회전할 때 그 위 점의 Y-coordinate 이 시간에 따라 보이는 궤적
◦
wave 의 period 는 원을 한 바퀴 회전할 때 소요되는 시간
Amplitude, Intensity
•
Amplitude
◦
Atmospheric
Complex Tones
•
frequency 는 수치로 나타낼 수 있는데 pitch 는 아님
Fourier Theorem
•
어떤 주기적인 신호도 sum of sinusoids 로 만들 수 있음
◦
amplitude 랑 phase 는 임의의 값을 가질 수 있으나, frequency 는 기본 주파수의 정수배의 것만 사용해서 만들어야 함
◦
는 fundamental, 는 harmonics
▪
fundamental 이 우리가 percept 하는 pitch 가 됨 (가장 낮은 주파수)
◦
harmonic frequency 로 구성된 sequence of sinusoids: harmonic frequency
Fourier Analysis
Fourier Series
•
급격한 변화가 있는 wave 는 매우 많은, 높은 frequency 의 wave 를 더해야 만들 수 있음
•
dirac delta function 의 경우, 무한개의 wave 가 필요
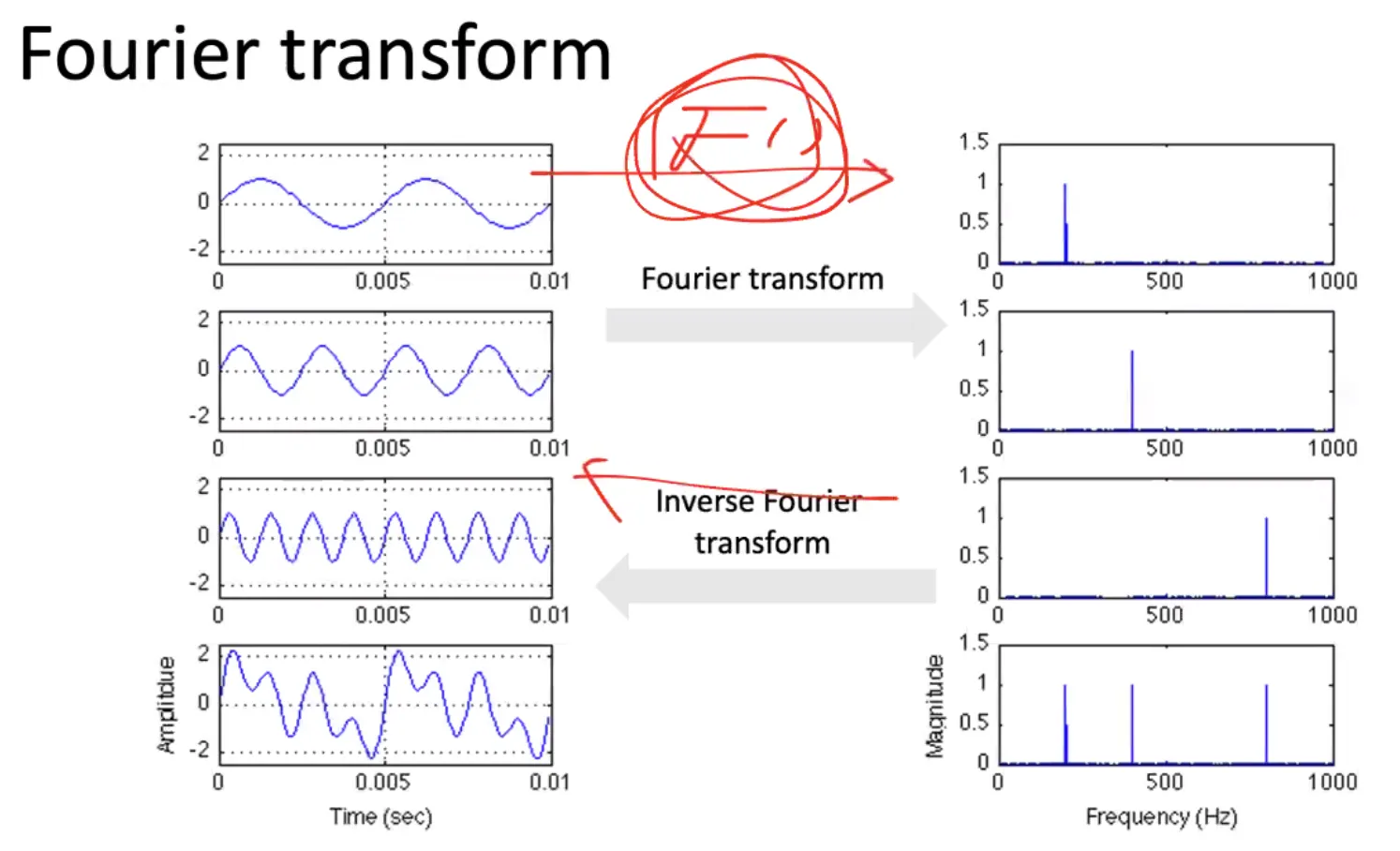
Fourier Transform
•
time domain 의 wave 를 주파수 domain 으로 변경하기 위한 것
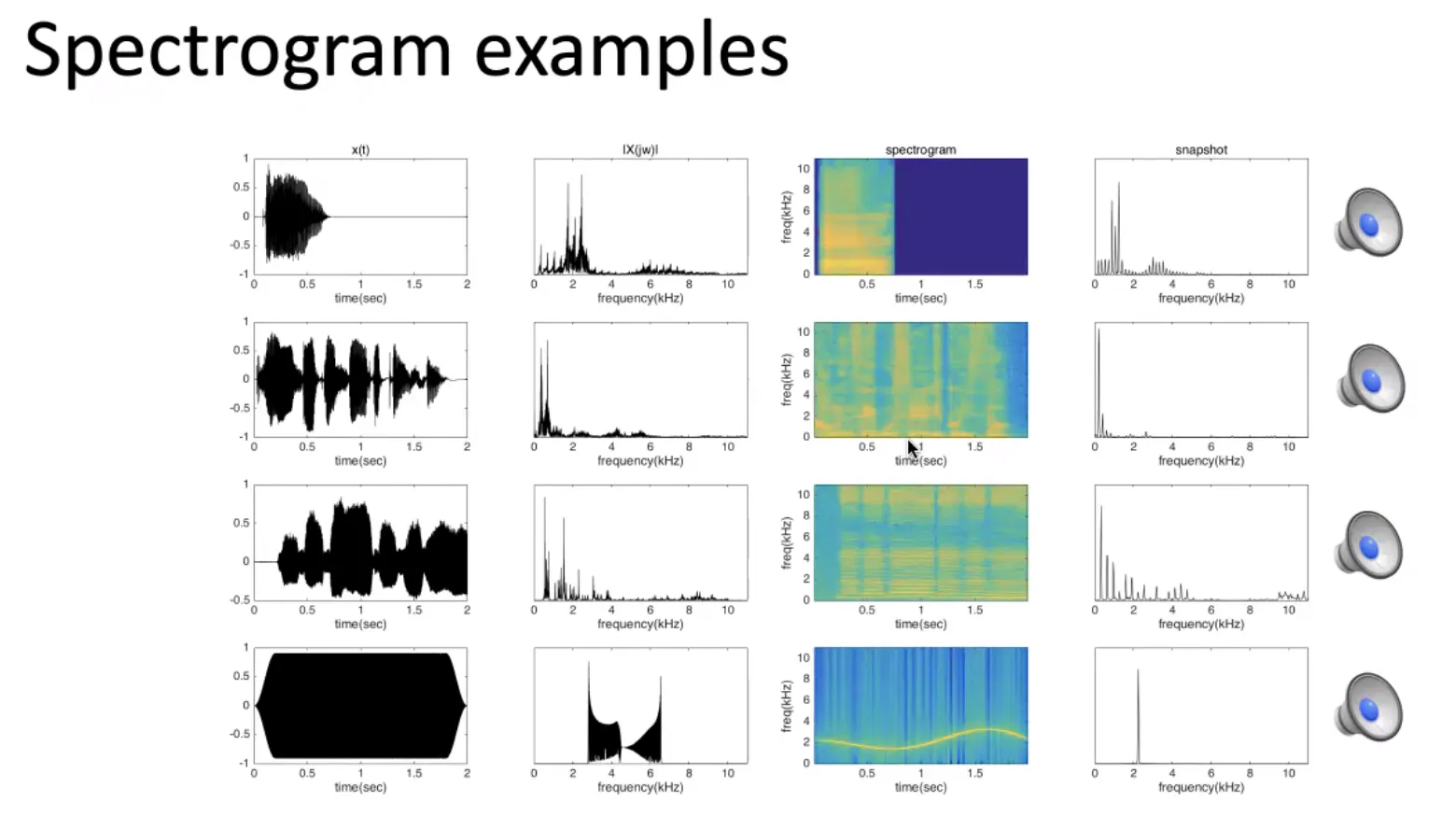
Spectrogram
•
frequency domain 으로 나타내면, frequency 들 간의 시간 순서를 알 수는 없음
◦
이를 해결하기 위해 만든 것이 spectrogram
•
short term time interval 의 주파수 성분을 표현
◦
시간에 따른 frequency 구성을 표현 (colormap 등으로 한 timestep 에서의 frequency 의 구성 자체도 표현할 수 있음)
Simple Harmonic Motion
•
ㅣ
Resonance
Sound Production in Speech
Wave Propagation
•
a
Reflection
Reverberation
•
Reverberation: 복잡한 echo (reflections) 들의 mixture 결과 (입체 음향?)
•
큰 공간 → reverberation time 이 김
dB SPL for common sounds
•
60dB: Conversation