Duplicate

Lecture 15 | Classification + SVM

형태
Machine Learning
수강 일자
2022/10/24

Recap: Supervised Learning: Classification

•
Binary classification 은 input x=(x1,...,xn)Tx =(x_1,...,x_n)^T 와 label t=(t1,...tn)Tt = (t_1,...t_n)^T (ti∈{0,1}t_i \in \{0,1 \})에 대해서 decision boundary 를 찾는 문제였음!
•
Linear Regression 과 같은 model 을 사용하는 것은 output 이 0 과 1 뿐인 binary classification 에는 적합하지 않음.
•
Sigmoid Function 은 output 을 0 ~ 1 사이로 압축해주기 때문에 0 과 1 로만 예측해야 하는 binary classification 에서 유용하게 사용될 수 있음.
◦
Linear Regression + Sigmoid 를 거친 값이 0.5 보다 크면 1로, 0.5 보다 작으면 0 으로 예측!
◦
Linear Regression 의 결과는 0 에서 판단의 경계를 가짐

Recap: Summary for Linear Classification

•
Logistic Regression
◦
σ(x)=11+e−x\sigma(x) = \frac{1}{1 + e^{-x}}
y=σ(z)=σ(wTx)y = \sigma(z)=\sigma(w^Tx)
◦
(Binary) Cross Entropy Loss
▪
Square Error 에 비해서 Cross Entropy 가 더 빠름! (log⁡(0∼1)\log (0\sim1) 까지가 굉장히 절댓값이 크기 때문)
▪
True value 가 1 이면 0 근처 value 를 크게 penalize 하고, true value 가 0 이면 1 근처 value 를 크게 penalize 함!
LCE=−tlog⁡y−(1−t)log⁡(1−y){\mathcal{L}}_{\rm CE} = -t\log y - (1-t)\log(1-y)
◦
Testing (예측)
▪
y=σ(z)=σ(wTx)>0.5→1y=\sigma(z)=\sigma(w^Tx) > 0.5 \rarr1
▪
y=σ(z)=σ(wTx)<0.5→0y=\sigma(z)=\sigma(w^Tx) < 0.5 \rarr0
•
Softmax Regression
z=Wxz = Wx
◦
Softmax σ(z)=ezi∑j=1Kezj\sigma(z)=\frac{e^{z_i}}{\sum_{j=1}^K e^{z_j}} → Softmax 의 결과값 항목을 다 더하면 1
◦
Cross Entropy Loss
LCE=−tTlog⁡y=−∑ktilog⁡yi{\mathcal{L}}_{\rm CE} = -t^T\log y = -\sum_k t_i\log y_i
◦
Testing (예측)
가장 큰 Softmax 값을 산출한 카테고리를 선택!

Logistic Regression: Probabilistic Perspective

•
Odds → 특정한 outcome 이 나올 likelihood 의 측정 (gambling 에서 자주 사용)
◦
이길 확률 / 질 확률
odds=p1−p{\rm odds} = \frac{p}{1-p}
◦
p>0.5p >0.5 (odds>1\rm odds > 1)이면 내가 이길 확률이 높다는 것이므로 참여해야 함.
•
Log Odds (Logit)
logit(p)=ln⁡p1−p{\rm logit(p)} = \ln \frac{p}{1-p}
◦
logit\rm logit 이 0 보다 크면 내가 이길 확률이 높다는 것이므로 참여해야 함.

Relation Between Logit (Log Odds) vs. Sigmoid Function

•
Sigmoid function 은 Logit 의 inverse
logit(p)=ln⁡p1−pelogit(p)=p1−p(1−p)elogit(p)=pelogit(p)=p(1+elogit(p))p=elogit(p)1+elogit(p)=11+e−logit(p)=σ(logit(p))\begin{align*} &{\rm logit}(p) = \ln \frac{p}{1-p} \\ &e^{{\rm logit}(p)}=\frac{p}{1-p} \\ &(1-p)e^{{\rm logit}(p)} = p \\ &e^{{\rm logit}(p)} = p (1+e^{{\rm logit}(p)})\\ &p = \frac{e^{{\rm logit}(p)}}{1 + e^{{\rm logit}(p)}} = \frac{1}{1 + e^{-{\rm logit}(p)}} = \sigma({\rm logit}(p)) \end{align*}
◦
Sigmoid function 이 logistic regression 에서 뜬금없이 등장한 것이 아니라 logit 컨셉에서부터 나온 것

Revisiting Logistic Regression

•
Logit function 을 hyperplane 에 fitting 하는 경우
logit(p)=ln⁡p1−p=wTx{\rm logit}(p) = \ln\frac{p}{1-p} = \rm w^Tx
•
pp 는 다음과 같이 나타내어짐
p=11+e−logit(p)=11+e−wTxp=\frac{1}{1 + e^{-{\rm logit}(p)}} = \frac{1}{1+e^{-\rm w^Tx}}
◦
이는 곧 logistic regression 에서의 결과값 (y=σ(z)=σ(wTx)y =\sigma(z) = \sigma(\rm w^Tx)) 이며, 이것이 probability of positive sample 임!
◦
p=P(t=1∣x)p = P(t=1|\rm x), 1−p=P(t=0∣x)1-p = P(t=0 | \rm x)
•
정리하자면, p=P(t=1∣x)p = P(t=1|\rm x), 1−p=P(t=0∣x)1-p = P(t=0 | \rm x) 로 정의하고, pp 에 대한 logit 을 hyperplane (wTx\rm w^Tx) 을 통해 fitting 을 하게 되면, 결과로 나오는 pp 가 sigmoid of hyperplane 임!
◦
p>0.5p > 0.5 일 때 positive 으로 예측 (logit(p)>0{\rm logit}(p) > 0 일 때 positive 으로 예측)

Recall: Probabilities vs. Likelihoods

•
Continous 한 probability distribution function 을 가지는 행위에 대해서 특정 행위가 나타날 확률은 0 임
•
Probability 는 고정된 distribution 의 아랫 영역
•
Likelihood 는 특정 데이터가 어떤 분포에서 가지는 등장 확률 yy 값
◦
데이터들을 가지고 있을 때, 실제 분포가 어떤 분포일지 예측하기 위해서는 Likelihood 를 최대로 가지는 분포를 실제 분포로 예측할 수 있음!
θ^=arg max⁡θ∈ΘLn(θ;x)\hat\theta = \argmax_{\theta\in\Theta} {\mathcal L}_n(\theta; \rm x)

Recall: MLE with Gaussian Distribution

•
Likelihood
◦
가진 데이터들의 likelihood 들의 총합
L(μ,σ2∣x)=p(x∣μ,σ2)=Πn=1NN(xn∣μ,σ2)L(\mu,\sigma^2|{\rm x}) =p({\rm x}|\mu,\sigma^2)=\Pi_{n=1}^N {\mathcal N}(x_n|\mu,\sigma^2)
•
Log-likelihood
ln⁡L(μ,σ2∣x)=ln⁡p(x∣μ,σ2)=−12σ2∑n=1N(xn−σ)2−N2ln⁡σ2−N2ln⁡(2π)\begin{align*} \ln L(\mu,\sigma^2|{\rm x}) &=\ln p({\rm x}|\mu,\sigma^2)\\ &=-\frac{1}{2\sigma^2}\sum_{n=1}^N (x_n-\sigma)^2 - \frac{N}{2}\ln\sigma^2-\frac{N}{2}\ln (2\pi) \end{align*}

Cost Function for Logistic Regression

•
p=P(t=1∣x)=11+e−wTxp=P(t=1|{\rm x}) = \frac{1}{1+e^-{\rm w^Tx}}
•
1−p=P(t=0∣x)1-p = P(t=0|\rm x)
•
위 두 개의 식을 묶어 간결하게 P(t∣x;w)=pt(1−p)1−tP(t|{\rm{x;w}}) = p^t(1-p)^{1-t} 로 나타낼 수 있음! (t∈{0,1}t \in \{0, 1\})
◦
x=(x1,...xN)T{\rm x} = (x_1,...x_N)^T 인 input
◦
t=(t1,...tN)T{\rm t} = (t_1, ... t_N)^T 인 target value (label)
•
조절 가능한 parameter 인 w\rm w 에 대한 데이터의 likelihood 는 다음과 같음
L(w)=P(t∣x;w)=∏i=1NP(ti∣xi;w)=∏i=1Npti(1−p)1−tiL({\rm w}) = P({\rm t|x;w}) = \prod_{i=1}^N P(t_i |x_i;{\rm w}) = \prod_{i=1}^N p^{t_i}(1-p)^{1-t_i}
•
조절 가능한 parameter 인 w\rm w 에 대한 데이터의 log-likelihood 의 maximize 는 cross entropy 를 minimize 하는 것과 같음!
log⁡L(w)=log⁡∏i=1Npti(1−p)1−ti=∏i=1Nlog⁡(pti(1−p)1−ti)=∑i=1Ntilog⁡pi+(1−ti)log⁡(1−pi)\log L({\rm w})=\log \prod_{i=1}^N p^{t_i}(1-p)^{1-t_i} = \prod_{i=1}^N \log (p^{t_i}(1-p)^{1-t_i}) = \sum_{i=1}^N t_i\log p_i +(1-t_i)\log (1-p_i)

Optimizing Logistic Regression

•
Prelimiary: Derivative of sigmoid function
σ′(z)=ddz11+e−z=1(1+e−z)2e−z=1(1+e−z)(1−11+e−z)=σ(z)(1−σ(z))\begin{align*} \sigma'(z) &= \frac{d}{dz}\frac{1}{1+e^{-z}}\\ &=\frac{1}{(1+e^{-z})^2}e^{-z}\\ &=\frac{1}{(1+e^{-z})}(1-\frac{1}{1+e^{-z}})\\ &= \sigma(z)(1-\sigma(z)) \end{align*}
•
Computing gradient considering the likelihood of one sample
◦
p=σ(wTx)p = \sigma({\rm w^Tx})
l(w)=tlog⁡p+(1−t)log⁡(1−p)l({\rm w})=t\log p+(1-t)\log(1-p)
∂∂wjl(w)=(t1σ(wTx)−(1−t)11−σ(wTx))∂∂wjσ(wTx)=(t1σ(wTx)−(1−t)11−σ(wTx))σ(wTx)(1−σ(wTx))=(t(1−σ(wTx))−(1−t)σ(wTx))xj=(t−σ(wTx))xj\begin{align*} \frac{\partial}{\partial w_j}l({\rm w}) &= (t\frac{1}{\sigma({\rm w^Tx)}}-(1-t)\frac{1}{1-\sigma({\rm w^Tx})})\frac{\partial}{\partial w_j}\sigma({\rm w^Tx}) \\ &=(t\frac{1}{\sigma({\rm w^Tx)}}-(1-t)\frac{1}{1-\sigma({\rm w^Tx})})\sigma({\rm w^Tx})(1-\sigma({\rm w^Tx})) \\ &= (t(1-\sigma({\rm w^Tx})) - (1-t)\sigma({\rm w^Tx}))x_j \\ &= (t-\sigma ({\rm w^Tx}))x_j \end{align*}
◦
Label 과 예측 값의 차이에 입력 값의 jj 번째 값을 곱한 값이 likelihood 의 wjw_j 에 대한 gradient!
•
Gradient Ascent (likelihood 를 maximize 하기 위해) 를 적용하면 다음과 같음!
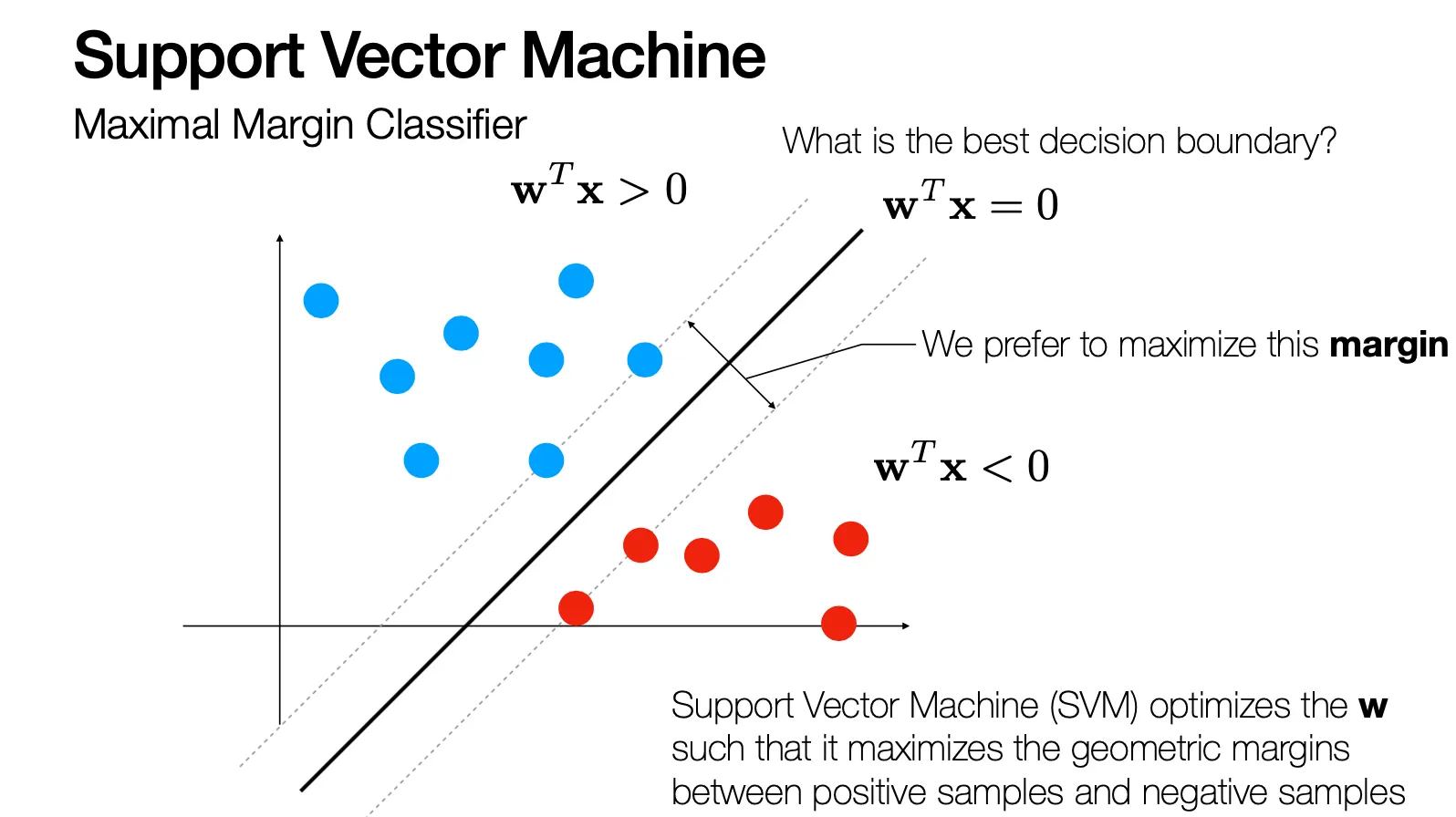
wj:=wj+αN∑i=1N(ti−σ(wTxi))(xi)jw_j:=w_j + \frac{\alpha}{N}\sum_{i=1}^N (t_i-\sigma({\rm w^Tx_i}))(x_i)_j

Support Vector Machine

•
Positive samples 와 negative samples 로 나눌 수 있는 boundary 를 찾는 문제
•
무엇이 가장 좋은 decision boundary 인가? → Margin 을 최대화 하는 decision boundary
•
Input: x=(x1,...,xN)T{\rm x} = (x_1, ..., x_N)^T where xi∈RDx_i \in {\mathbb R}^D
•
Label: t=(t1,...,tN)T{\rm t} = (t_1,...,t_N)^T where ti∈{−1,1}t_i \in\{-1,1 \}
•
Decision boundary equation: wTx+b=0{\rm w^Tx} + b =0 → w\rm w 는 perpendicular vector!
◦
wTx1+b=0{\rm w^Tx_1 } + b =0 and wTx2+b=0{\rm w^Tx_2} + b = 0 → wT(x1−x2)=0{\rm w^T (x_1-x_2)} = 0
◦
Unit perpendicular vector 는 w∥w∥\frac{\rm w}{\| \rm w\|}
•
특정 점 xi{\rm x_i} 에서 hyperplane 에 내린 수선의 발 점이 xi′{\rm x_i'} 라고 할 때, 두 점 사이의 관계는 다음과 같음!
xi−γiw∥w∥=xi′{\rm x_i} - \gamma_i \frac{{\rm w}}{\|{\rm w} \|} = {\rm x_i'}
◦
해당 xi′{\rm x_i'} 는 hyperplane 위에 있으므로 다음이 성립함!
wT(xi−γiw∥w∥)+b=0{\rm w^T}({\rm x_i} - \gamma_i \frac{{\rm w}}{\|{\rm w} \|}) + b =0
◦
xi{\rm x_i} 로부터 hyperplane 까지의 거리 γ\gamma 은 다음과 같음!
γi=wTxi+b∥w∥\gamma_i =\frac{{\rm w^Tx_i} + b}{\| {\rm w} \|}
◦
positive 와 negative 모두를 고려한 식은 ti∈{−1,1}t_i \in\{-1,1 \} 에 대해 다음과 같음!
γi=ti(wTxi+b∥w∥)\gamma_i =t_i (\frac{{\rm w^Tx_i} + b}{\| {\rm w} \|})
◦
가장 가까운 거리를 가지는 xi{\rm x_i} 에 대한 거리는 γ=min⁡iγi\gamma = \min_i \gamma_i
◦
가장 가까운 거리를 가장 길게 만드는 w∗=arg max⁡wγ{\rm w^*} = \argmax_{\rm w} \gamma 를 구해야함!
•
SVM 의 최종 목표는 가장 가까운 거리의 점간의 거리가 최대가 되는 w∗{\rm w^*} 를 구하는 것!
w∗=arg max⁡w(min⁡iti(wTxi+b∥w∥))=arg max⁡w1∥w∥(min⁡iti(wTxi+b))\begin{align*} {\rm w^*} &= \argmax_{\rm w} (\min_i t_i (\frac{{\rm w^Tx_i} + b}{\| {\rm w} \|}) ) \\ &= \argmax_{\rm w} \frac{1}{\|{\rm w} \|} (\min_i t_i ({\rm w^Tx_i} + b) ) \\ \end{align*}
◦
여기서 모든 경우에서 해당 w{\rm w} 와 bb 에 scalar 를 곱해서 min⁡iti(wTxi+b)=1\min_i t_i ({\rm w^Tx_i} + b) = 1 이 되도록 변경할 수 있고 이 과정이 w{\rm w} 와 bb 로 결정되는 hyperplane 에 영향을 주지 않기 때문에 이러한 constraint 를 줄 수 있음!
w∗=arg max⁡w1∥w∥ where ti(wTxi+b)≥1\begin{align*} {\rm w^*} &= \argmax_{\rm w} \frac{1}{\|{\rm w} \|} \end{align*} \space {\rm where} \space t_i({\rm w^Tx_i}+ b) \ge 1
◦
이는 더불어 minimizing problem 으로 바꿀 수도 있음! (Linear 하게 두 영역을 separate 가능할 때만 이러한 변경이 가능)
w∗=arg min⁡w12∥w∥ where ti(wTxi+b)≥1\begin{align*} {\rm w^*} &= \argmin_{\rm w} \frac{1}{2} \| {\rm w}\| \end{align*} \space {\rm where} \space t_i({\rm w^Tx_i}+ b) \ge 1
◦
Linearly separable 하지 않은 경우에 대한 대응은 다음과 같음.
▪
slack variables ξi≥0\xi_i \ge 0, violator point 에 대해서만 non-zero ξ\xi 값을 가짐
▪
ξi>0\xi_i>0 으로 된 점들에 대해서는 margin 안쪽에 있음! (다만, margin 안쪽에 있는 경우가 식을 최대로 만들어야 함)
▪
ti(wTxi+b)≥1−ξit_i({\rm w^Tx_i}+ b) \ge 1-\xi_i
w∗=arg min⁡w,ξ12∥w∥+C∑nξn\begin{align*} {\rm w^*} &= \argmin_{{\rm w}, \xi} \frac{1}{2}{\|{\rm w} \|} +C\sum_n \xi_n \end{align*}
▪
높은 CC 는 margin violation 을 크게 penalize 함 (Hard Margin)
▪
낮은 CC 는 margin violation 을 어느정도는 허용함 (Soft Margin)