Variational Auto Encoder (VAE)

태그
Auto Encoder
포스팅 날짜
2021/11/02
[주의] 해당 세션은 생각보다 어려울 수 있습니다. 가볍게만 들어주셔도 무방합니다.
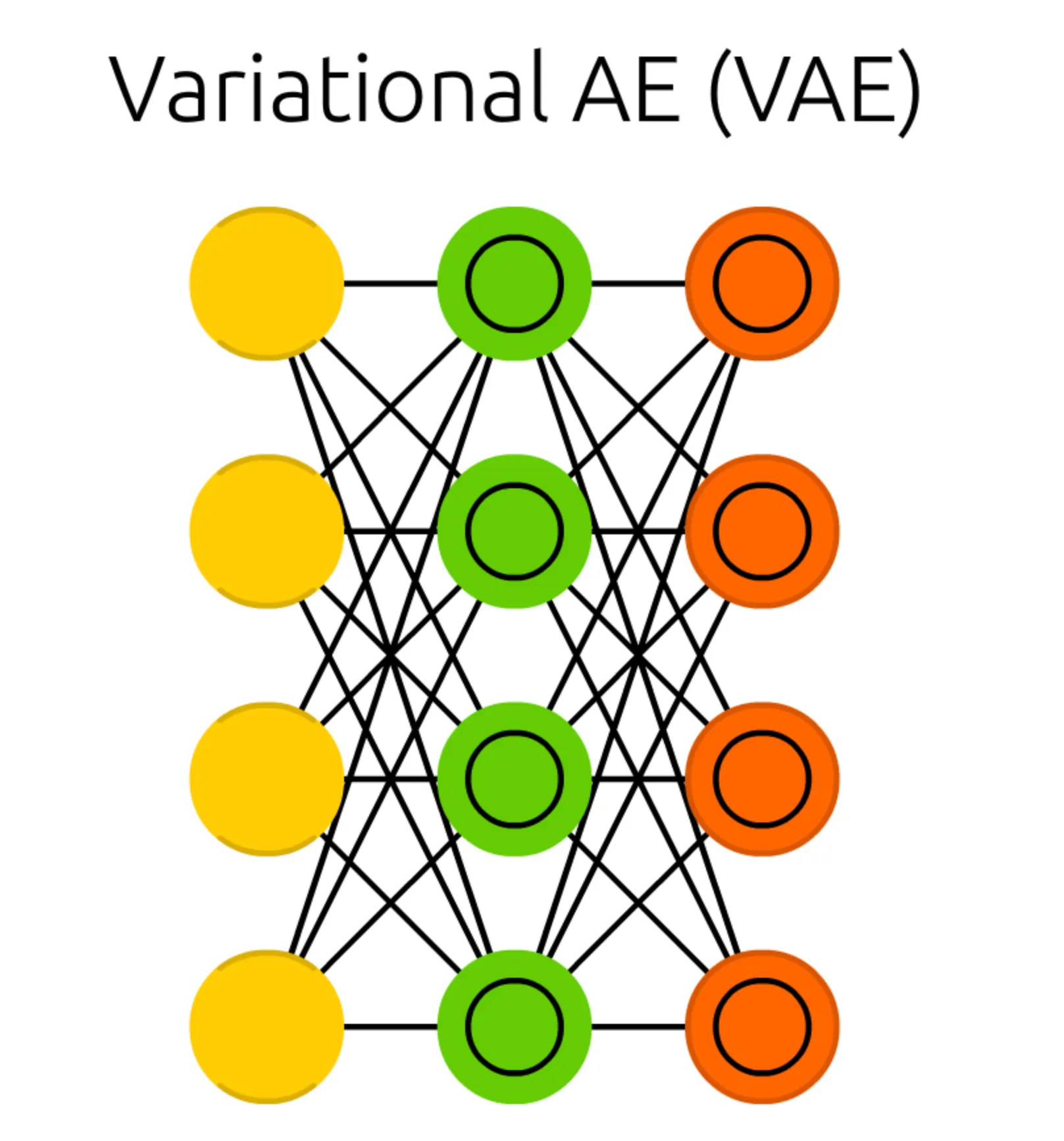
본 세션에서는, 이전 세션에서 언급했던 AE 와 유사한 형태의 네트워크인 Variational Auto Encoder (VAE)에 대해서 알아보려고 합니다.
가장 먼저 보이는 구조의 특징적인 변화는 Hidden Cell 이 있던 위치에, 내부에 동심원이 그려진 다른 Cell 이 존재한다는 점입니다. 이러한 형태의 Cell 을 Probabilistic Hidden Cell 이라고 합니다. 더불어 이전의 Auto Encoder (AE) 에서는 두 가지 제약 조건이 존재한다고 말씀드렸었는데 그 중 Hidden Cell 의 dimension 이 Match Input Output Cell 보다 작아야 한다는 조건이 있었습니다. 하지만, 여기서는 보기에 그렇게 보이지 않습니다.
그렇다면 Hidden Cell 에서 Probabilistic Hidden Cell 로 바뀐 것에는 어떤 차이가 있는 걸까요?
이전 Auto Encoder (AE) 에서는 input 의 표현형을 잘 나타내는 latent vector 값을 가지는 것이 Hidden Cell 이라고 소개를 드렸습니다. 따라서, reconstruction loss 를 이용해서 학습을 진행했고 성공적으로 latent vector 값을 산출할 수 있었습니다.
다만, Variational Auto Encoder (VAE) 에서 얻어내려고 하는 것은 input 의 표현형을 잘 나타내는 latent vector 가 아닙니다. 앞선 Auto Encoder (AE) 세션의 마지막에 언급했듯, Variational Auto Encoder (VAE) 는 Generational Model 입니다. Variational Auto Encoder (VAE) 에서 목적으로 하는 것은 training dataset 에 존재하는 데이터와 유사한 output 을 생성해내는 네트워크를 구현하는 것입니다.
이 때, 유사하다- 라는 개념을 통계학적으로 해당 training dataset 이 가지는 데이터 확률 분포를 따른다- 로 볼 수 있습니다. 하지만, training dataset 이 어떤 확률 분포를 따르는지 아는 것은 굉장히 어려운 일입니다. Dataset 의 개수는 물론 data 하나하나가 가지는 data 의 수도 많기 때문에 이를 전체적으로 설명할 수 있는 좋은 확률 분포를 찾는 일이기 때문입니다. 딥러닝은 이러한 복잡하고 어려운 문제를 해결하기 위해 사용한다고 이전에 Deep Feed Forward Network (DFF) 를 설명할 때 언급했던 경험이 있습니다. 이처럼, Variational Auto Encoder (VAE) 에서의 Hidden Cell 은 training dataset 을 잘 설명하는 확률 분포이기 때문에 Probabilistic 이라는 구문이 붙었다고 보시면 됩니다.
정리하자면, Variational Auto Encoder (VAE) 에서는 training dataset 을 잘 설명할 수 있는 확률 분포를 학습하는 것이 목적입니다. 다만, 아직은 확률 분포를 학습한다는 개념이 쉽게 이해되지 않을 수도 있습니다. (저도 처음에 그랬습니다.)
하지만, Maximum Likelihood Estimation (MLE) 를 떠올리면 이해하기가 한결 쉬우실 것입니다. 통계를 배울때 저희는 데이터를 보고 해당 데이터가 따르는 확률 분포를 찾는 행위를 많이 진행했었습니다. 그 때 가장 기본적으로 적용했던 방법이 Maximum Likelihood Estimation 입니다.
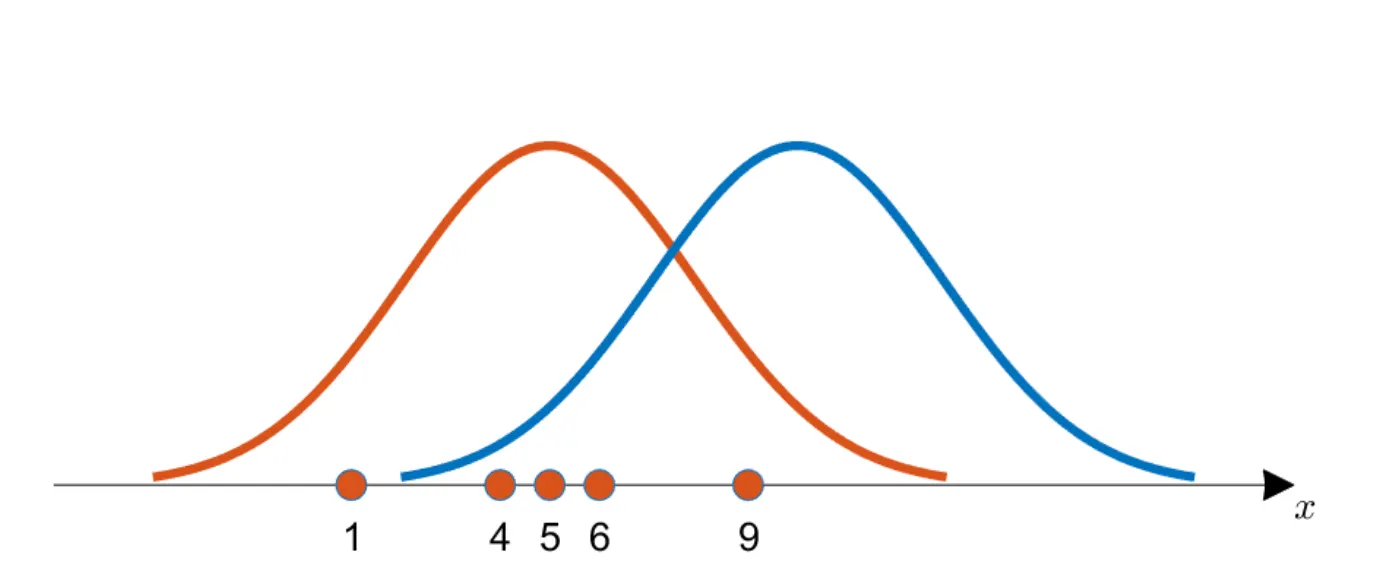
간단한 예시를 들어보겠습니다. 관측해낸 데이터가 다음과 같다고 가정해봅시다.
x={1,4,5,6,9}x = \{ 1, 4, 5, 6, 9\}
이 때 아래와 같은 두 확률 분포 1(주황색) 과 2(파랑색) 중 xx 라는 확률변수는 어느 확률 분포를 따를 것 처럼 보이시나요?
대충 보기에도 주황색 확률분포를 따를 것만 같지 않으신가요? 이렇게 느끼시는 이유는 해당 확률분포가 관측 데이터를 더 잘 설명한다고 느끼기 때문입니다. 그리고 확률분포를 잘 설명한다고 하면, 실제로 해당 확률분포에서 sampling 을 해서 데이터를 뽑았을 때 관측 데이터의 분포가 나올법하다- 라는 것과 상통하는 의미로 해석할 수 있습니다.
Maximum Likelihood Estimation (MLE) 는 위의 의미를 수식화한 것입니다. 확률분포의 선택지들 중에서 sampling 을 거쳤을 때 해당 데이터의 분포가 나올 확률이 높은 것을 선택하는 방법론인 것입니다. 이를 수식으로 나타내면 다음과 같습니다.
arg max⁡θ∏i=1Npθ(xi)\argmax_{\theta}\prod_{i=1}^Np_{\theta}(x_i)
확률분포를 정의하는 변수 θ\theta 에 대해서 관측 데이터의 조합이 나올 확률을 최대로 만드는 θ\theta 의 조합을 찾아내는 것입니다. 그런데, 여기서 눈치 빠른 분은 아셨겠지만, 딥러닝에서 최소화 및 최대화를 하는 방법으로 gradient descent 가 있죠? 따라서 대략적인 설명으로 Variational Auto Encoder (VAE) 는 gradient descent 를 이용해서 training dataset 이 나올 확률을 최대로 만드는 방향으로 weight 를 학습해나간다- 라고 보시면 됩니다.
하지만, Variational Auto Encoder (VAE) 에서 해당 방법으로 학습을 진행하기에는 큰 문제가 있습니다.
Training data 이자 output 으로 나오길 원하는 데이터가 그냥 딱 나오는 것이 아니라 생성의 기반이 될 vector 에 conditional 하게 등장한다는 점입니다.
이게 무슨 소린가 하면...
Variational Auto Encoder (VAE) 에서 원하는 것이 training data 를 잘 표현하는 확률 분포인 것은 맞으나, 학습의 결과가 확률분포를 정의하기 위한 요소는 아닙니다. Training data 의 확률분포가 기존의 gaussian 등의 확률분포를 따른다는 가정이 있다면, 평균과 분산을 학습하는 형태로 확률분포 자체를 결과로 내는 네트워크가 가능하겠지만, 어떤 분포를 따르는지도 모르는데 분포를 나타내는 parameter 를 학습해낼 순 없다는 것입니다.
그렇다면, Variational Auto Encoder (VAE) 의 학습 결과는 무엇일까요?
정답은 이미지입니다. 설명을 덧붙이자면, 이 결과로 나온 이미지가 training dataset 으로 학습한 분포에 최대한 들어맞길 원하는 것입니다. 때문에 단순히 training dataset 과 output 으로 나온 이미지의 차이를 작게 하는 일반적인 형태의 학습을 생각하시면 안됩니다. Loss 이자 목표는 위에 설명드린 training dataset 과 찾고자 하는 분포의 likelihood 의 최대화입니다.
다시 한 번 강조하자면, 궁극적으로 네트워크는 training data 를 잘 표현하는 확률 분포를 따를 것만 같은- output data 를 생성해야합니다. 이러한 생성 능력을 네트워크에 부여하기 위해서 잘 생성했는지 아닌지의 척도가 되는 것이 앞서 이야기드렸던 Maximum Likelihood Estimation (MLE) 의 최적화인 것입니다.
요약하자면, 사실은 Variational Auto Encoder (VAE) 에서 다루고자 하는 문제는 training data 가 잘 따를 것 같은 확률분포를 찾는 단순한 문제가 아니라, 어떠한 input vector zz 에 대해서도 그 생성 결과가 training data 들일 확률의 production 의 최대화입니다. 기존에 간단하게 설명드린 예시에서는 해당 training data 가 특정 θ\theta 에 대해서 등장할 확률만을 이야기 드린 것이라면, 실제로는 zz 로부터 해당 training data 가 생성될 확률과 해당 training data 가 θ\theta 에 대해서 mapping 된 분포에서 등장할 확률을 곱해서 종합적으로 θ\theta 를 얼마나 penalize 할 것인지 정한다고 보시면 됩니다. 이를 수식으로 나타내면 다음과 같습니다.
arg max⁡θ∏i=1Npθ(xi)=arg max⁡θ∏i=1N∫pθ(xi∣z)pθ(z)dz\argmax_{\theta}\prod_{i=1}^N p_{\theta}(x_i)=\argmax_{\theta}\prod_{i=1}^N \int p_{\theta}(x_i|z)p_{\theta}(z)dz
그리고, 최종적인 목표는 위와 같지만, 하나의 학습 데이터 xix_i 에 대해서 weight update 의 목표는 다음과 같게 됩니다.
arg max⁡θ∫pθ(xi∣z)pθ(z)dz\argmax_{\theta}\int p_{\theta}(x_i|z)p_{\theta}(z)dz
여기서 Variational Auto Encoder (VAE) 의 학습에 Maximum Likelihood Estimation (MLE) 를 적용하는 것의 문제점이 나타납니다. 해당 식을 계산하거나 할 수 있어야 미분을 하여 gradient descent 를 적용할텐데, 어떤 분포를 따르는지도 모르는 zz 에 대해 해당 값을 계산할 수 없습니다. 설령 zz 를 gaussian 등의 분포로 가정한다고 해도 실제로 저걸 계산하려면 input zz 를 매우 다양하게 넣어가면서 통계적으로 값을 구하는 수밖에 없습니다. 이를 Monte Carlo Method 이자 저희에게 큰 수의 법칙으로 알려진 친구입니다.
이를 해결하기 위해서 Variational Auto Encoder (VAE) 는 1차적으로 Bayes Theorem 이라는 아이디어를 고안합니다. zz 라는 알 수 없는 변수를 조건부 확률로 가지는 식보다는 가지고 있는 데이터인 xix_i 를 조건부 확률로 가진 식으로 변경해보겠다는 시도입니다.
pθ(xi∣z)=pθ(z∣xi)pθ(xi)pθ(z)p_{\theta}(x_i|z)=\frac{p_{\theta}(z|x_i)p_{\theta}(x_i)}{p_{\theta}(z)}
하지만, 여기서도 pθ(xi)p_{\theta}(x_i) 가 구할 수 없는 값이 되어버립니다. 사실 이걸 알았다면 제일 첫 식에서 사용을 할 수 있었습니다. 결과적으로, 목표는 정했지만, 이것을 계산할 수 없는 현상이 나타났고, 이러한 현상을 Intractability 라고 합니다. (직역했을 때 계산불가능성- 이라고 보시면 됩니다.)
Variational Auto Encoder (VAE) 는 해당 Intractability 를 해결하기 위해 다시 근본으로 돌아가 사후확률을 근사해서 계산해내기로 합니다.
pθ(xi)=pθ(xi∣z)pθ(z)pθ(z∣xi)p_{\theta}(x_i) = \frac{p_{\theta}(x_i|z)p_{\theta}(z)}{p_{\theta}(z|x_i)}
위 식에서 pθ(xi∣z)p_{\theta}(x_i|z) 는 학습할 네트워크이므로 주어진 zz 와 θ\theta 에 대해서는 계산이 가능하고, pθ(z)p_{\theta}(z) 는 gaussian 이라고 가정을 하면, 모르는 부분은 pθ(z∣xi)p_{\theta}(z|x_i) 뿐이기 때문에 이를 앞선 pθ(xi∣z)p_{\theta}(x_i|z) 에서 처럼 네트워크화 시켜 구현할 생각을 하게 된 것입니다.
이러한 생각으로 Auto Encoder (AE) 와 같이 pθ(z∣xi)p_{\theta}(z|x_i) (사후확률, posterior)를 계산하기 위한 encoder 부분과 pθ(xi∣z)p_{\theta}(x_i|z) (likelihood) 를 계산하기 위한 decoder 부분이라는 구조가 탄생하게 된 것입니다.
이 때 중요하게 짚고 넘어가야 할 점은, 앞선 pθ(xi∣z)p_{\theta}(x_i|z) 등은 주어진 zz 와 θ\theta 에 대해서만 계산이 가능하기 때문에 encoder 는 다양한 zz 를 산출해줄 수 있어야 한다는 점입니다. 때문에 encoder 에서 학습하는 것은 zz 값을 gaussian 등으로 가정했을 때 zz 값을 뽑아낼 수 있는 sampling 함수를 정의하기 위한 요소입니다.
이게 무슨 소리냐!
하면, gaussian 의 mean 과 variance 를 encoder 에서 학습하고 decoder 에 들어가기 전에 해당 분포로부터 sampling 을 진행해야 분자의 요소들을 계산해낼 수 있다는 것입니다. 결과적으로, 실제 pθ(z∣xi)p_{\theta}(z|x_i) 는 알 수 없으니깐 해당 친구를 학습을 통해서 구하려는 시도인 것입니다. 그리고 이 과정을 Variational Inference (변분추론) 이라고 부릅니다.
Variational Inference 의 아이디어는 p(z∣xi)p(z|x_i) 가 알려진 확률분포가 아니기 때문에 네트워크의 weight ϕ\phi 를 기반으로 산출해내는 sampling 함수 qϕ(z∣xi)q_{\phi}(z|x_i) 라는 확률분포로 근사하여 식을 전개하는 것입니다. 이러한 근사를 가정하면, 처음에 제시했던 식의 최대화는 다음과 같이 변화할 수 있습니다.
log⁡p(x)=∫log⁡(p(x))qϕ(z∣x)dz=∫log⁡(p(x,z)p(z∣x))qϕ(z∣x)dz=∫log⁡(p(x,z)qϕ(z∣x)⋅qϕ(z∣x)p(z∣x))qϕ(z∣x)dz=∫log⁡(p(x,z)qϕ(z∣x))qϕ(z∣x)dz+∫log⁡(qϕ(z∣x)p(x,z))qϕ(z∣x)dz=ELBO(ϕ)+KL(qϕ(z∣x)∣∣p(x,z))\begin{align*} \log p(x)&=\int\log(p(x))q_{\phi}(z|x)dz \\ &= \int\log(\frac{p(x,z)}{p(z|x)})q_{\phi}(z|x)dz \\ &= \int\log(\frac{p(x,z)}{q_{\phi}(z|x)}\cdot\frac{q_{\phi}(z|x)}{p(z|x)})q_{\phi}(z|x)dz \\ &= \int\log(\frac{p(x,z)}{q_{\phi}(z|x)})q_{\phi}(z|x)dz + \int\log(\frac{q_{\phi}(z|x)}{p(x,z)})q_{\phi}(z|x)dz \\ &= \rm{ELBO(\it{\phi})} + KL(\it{q_{\phi}(z|x) || p(x,z)}) \end{align*}
이때, KL(qϕ(z∣x)∣∣p(x,z))\rm{KL}(\it{q_{\phi}(z|x) || p(x,z)}) 는 두 확률분포의 차이를 구해내는 식으로 보시면 됩니다. 다만, p(x,z)p(x,z) 를 정확하게 규명할 수 없는 상황이기 때문에 Variational Auto Encoder (VAE) 에서는 ELBO(ϕ)\rm{ELBO(\it{\phi})} 를 최대화 하는 것을 목적으로 진행합니다.
그렇다면 ELBO(ϕ)\rm{ELBO(\it{\phi})} 를 최대화하는 것은 어떤 의미를 가지는지 전개해볼까요?
ELBO(ϕ)=∫log⁡(p(x,z)qϕ(z∣x))qϕ(z∣x)dz=∫log⁡(p(x∣z)p(z)qϕ(z∣x))qϕ(z∣x)dz=∫log⁡(p(x∣z))qϕ(z∣x)dz−∫log⁡(qϕ(z∣x)p(z))qϕ(z∣x)dz=Eqϕ(z∣x)log⁡(p(x∣z))−KL(qϕ(z∣x)∣∣p(z))\begin{align*} \rm{ELBO(\phi)} &= \int\log(\frac{p(x,z)}{q_{\phi}(z|x)})q_{\phi}(z|x)dz \\ &= \int\log(\frac{p(x|z)p(z)}{q_{\phi}(z|x)})q_{\phi}(z|x)dz \\ &= \int\log(p(x|z))q_{\phi}(z|x)dz - \int\log(\frac{q_{\phi}(z|x)}{p(z)})q_{\phi}(z|x)dz \\ &= \mathbb{E_{q_{\phi(z|x)}}}\log(p(x|z))-\rm{KL}(\it{q_{\phi}(z|x) || p(z)}) \end{align*}
ELBO(ϕ)\rm{ELBO(\it{\phi})} 전개의 마지막 줄을 살펴봅시다.
Eqϕ(z∣x)log⁡(p(x∣z))\mathbb{E_{q_{\phi(z|x)}}}\log(p(x|z)) 는 그대로 해석하자면, training data xx 에 대해 학습한 ϕ\phi 를 통해 찾아낸 sampling 함수 qϕq_{\phi} 를 따르는 변수 zz 에 대해서 다시 θ\theta 를 통해 재구성해낸 것들 중 얼마나 많은 것들이 다시 xx 인 것인가를 나타내는 항목입니다. 한 마디로 요약하면 Reconstruction Term 이라고 볼 수 있고 이를 크게 만들어야 합니다. 실제로 해당 항목은 Cross Entropy Loss 와 동일합니다.
KL(qϕ(z∣x)∣∣p(z))\rm{KL}(\it{q_{\phi}(z|x) || p(z)}) 는 그대로 해석하자면, 정확히 알지 못했던 p(z∣xi)p(z|x_i) 를 근사하기 위해 설계했던 sampling 함수 qϕq_{\phi} 가 사용할 prior distribution 인 p(z)p(z) 과 얼마나 비슷한가를 나타내는 항목입니다. 한 마디로 요약하면 Regularization Term 이라고 볼 수 있고 (dataset 에 특화된 overfitting 방지하고 가정한 일반적인 분포 (여기서는 gaussian) 와 비슷한 sampling 함수를 찾아내는 것입니다.) 이를 작게 만들어야 합니다.
내용이 길었습니다. Variational Auto Encoder (VAE) 의 핵심적인 내용을 요약하면 다음과 같습니다.
1.
Variational Auto Encoder (VAE) 의 정성적인 목적은 training dataset 과 유사한 이미지를 생성해내는 것입니다.
2.
Variational Auto Encoder (VAE) 의 정량적인 목적은 training dataset 의 등장 가능성을 최대화하는 네트워크의 구현입니다. (MLE 관점)
3.
Variational Auto Encoder (VAE) 는 일반적인 MLE 와는 달리 input 에 conditional 한 output 의 분포가 training dataset 을 가장 잘 설명하도록 하는 네트워크 parameter 를 학습해야 하는데, 이는 특정 분포를 따르는 input 에 대한 모든 경우를 넣어야 하기 때문에 intractable 합니다. Bayes Theorem 을 써서 변경하더라도 마찬가지입니다.
4.
Bayes Theorem 을 통해 변경한 식에서 유일하게 intractable 한 사후확률(posterior distribution)을 항목을 학습을 통해서 구해낼 수 있을 것이라는 아이디어를 실현시킵니다. 이를 Variational Inference 이라고 부릅니다.
5.
결과적으로, 사후확률분포를 산출하고 해당 사후확률분포에서 sampling 을 통해 latent vector 을 뽑아낸 뒤에 해당 vector 들이 input 으로 들어간 네트워크가 산출할 값이 처음에 input 으로 넣었던 친구일 확률을 최대화하는 것은 Negative Log Likelihood 를 최소화하는 것과 같고 이는 Cross Entropy 의 최소화를 통해 구해낼 수 있습니다. 더불어 overfitting 을 방지하기 위한 regularization term 을 두어 mean, variance 가 너무 튀는 것을 방지하는 요소로 해석할 수 있는 Loss term 도 있습니다. 이 loss term 을 최소화하는 방향으로 학습을 진행하게 되는 것입니다.
마지막으로 언급드릴 내용은 5 번의 사후확률분포로부터 sampling 을 하는 과정은 differentiable 한 과정이 아니라는 점입니다. Variational Auto Encoder (VAE) 에서는 이를 해결하기 위해 sampling 대신 reparametrization trick 이라는 기법을 사용합니다.
이는 상당히 간단합니다. 사후확률분포를 gaussian 으로 가정한 뒤에 mean 과 variance 를 학습했다고 가정합시다. 그렇다면 sampling 과정은 다음과 같습니다.
z∼N(μ,σ)z \sim N(\mu,\sigma)
이것과 동일한 효과를 내면서 미분 가능한 연산으로 다음과 같이 reparametrization trick 을 적용할 수 있습니다.
z=μ+σ⋅ϵwhere ϵ∼N(0,1)\begin{align*} &z = \mu + \sigma\cdot\epsilon \\ &\rm{where\ } \epsilon \sim \it{N}(\rm{0,1}) \end{align*}
이렇게 이번 세션에서는 Variational Auto Encoder (VAE) 에 대해서 알아보는 시간을 가졌습니다. Variational Auto Encoder (VAE) 의 목적이 training dataset 을 잘 설명하는 확률분포를 따르는 output 의 생성이고, 이를 위해서 MLE 를 사용했다는 점과 MLE 의 intractability 때문에 사후확률을 Variational Inference 로 구해냈다는 점을 주요하게 알아두시면 좋을 것 같습니다.

Cross Entropy 와 MLE 의 관계

Entropy?

열역학: 불확정성, 무질서도 정보이론: 평균 정보량(정보량의 기댓값)
"잘 일어나지 않는 사건은 잘 일어나는 사건보다 정보량이 많다"
ex) 오늘 7시에 천둥번개가 친다는 정보는 오늘 7시에 해가 진다는 정보보다 정보량이 많음
어떤 확률분포 p(x)p(x) 를 따르는 확률변수 XX 가 가지는 정보량이 얼마나 될까?
Hp(x)=−∑xp(x)log⁡p(x)=∑xp(x)log⁡1p(x)=EX∼p(x)[log⁡1p(x)]\begin{align*} H_p(x) &= -\sum_x p(x)\log p(x)\\ &=\sum_x p(x)\log\frac{1}{p(x)}\\ &=\mathbb{E}_{X\sim p(x)}[\log\frac{1}{p(x)}] \end{align*}

Cross Entropy?

두 분포 사이의 평균 정보량
"p(x)p(x) 라는 분포를 따르는 확률 변수 XX 에 대해서 새로운 q(x)q(x) 가 가지는 정보량"
Hp,q(x)=−∑xp(x)log⁡q(x)=∑xp(x)log⁡1q(x)=EX∼p(x)[log⁡1q(x)]\begin{align*} H_{p,q}(x) &= -\sum_x p(x)\log q(x) \\ &=\sum_x p(x)\log\frac{1}{q(x)}\\ &=\mathbb{E}_{X\sim p(x)}[\log\frac{1}{q(x)}] \end{align*}
Cross Entropy 는 KL-divergence 와 p(x)p(x) 의 entropy 의 합
Hp,q(x)=−∑xp(x)log⁡q(x)=∑xp(x)log⁡1q(x)=∑xp(x)log⁡p(x)q(x)−∑xp(x)log⁡p(x)=DKL(p∣∣q)+Hp(x)\begin{align*} H_{p,q}(x) &= -\sum_x p(x)\log q(x) \\ &=\sum_x p(x)\log\frac{1}{q(x)}\\ &= \sum_x p(x)\log\frac{p(x)}{q(x)}-\sum_x p(x)\log p(x)\\ &= D_{KL}(p||q) + H_p(x) \end{align*}
Cross Entropy 의 최소화는 pp 와 qq 의 분포차이인 DKL(p∣∣q)D_{KL}(p||q) 를 작게 만드는 방향

MLE?

가지고 있는 데이터를 가장 잘 설명할 수 있는 확률 분포를 찾아내는 방법
arg max⁡θ∏i=1Npθ(xi)=arg max⁡θ∑i=1N1Nlog⁡pθ(xi)=arg max⁡θEX∼pdata(x)log⁡pθ(x)=arg min⁡θEX∼pdata(x)[log⁡1pθ(x)]\begin{align*} \argmax_{\theta}\prod_{i=1}^Np_{\theta}(x_i) &= \argmax_{\theta}\sum_{i=1}^N \frac{1}{N} \log p_{\theta}(x_i)\\ &=\argmax_{\theta}\mathbb{E}_{X\sim p_{data}(x)} \log p_{\theta}(x)\\ &= \argmin_{\theta}\mathbb{E}_{X\sim p_{data}(x)} [\log \frac{1}{p_{\theta}(x)}] \end{align*}
MLE 를 목적으로 진행한 학습은, Cross Entropy 의 최소화를 목적으로 가지는 것과 같고 이는 결론적으로 학습된 데이터의 분포를 학습 데이터의 분포와 유사하게 만드는 방향으로 진행
실제 학습에서는, 각 픽셀별 값을 0 ~ 1 사이로 변환한 값을 (일반적으로 255 로 나눔) ground truth p(x)p(x) 로, 학습과정에서 나온 output 의 해당 픽셀 값을 q(x)q(x) 로 하여 이들을 모두 다 더해서 Cross Entropy 를 계산