Duplicate

Lecture 9 | More Single View Geometry

수강 일자
2023/02/26

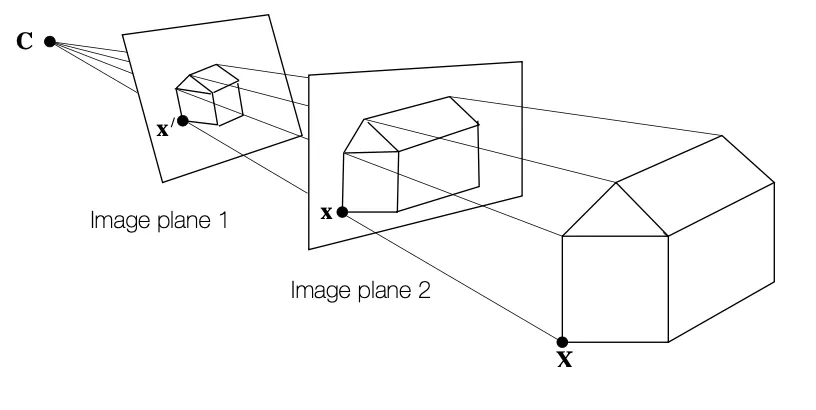
Projecting a 3D Scene Plane

[xy1]=K[r1 r2 r3 t][XY01]=K[r1 r2 t][XY1]=H[XY1]\begin{bmatrix} x \\ y \\ 1 \end{bmatrix} =K[r_1\ r_2\ r_3\ {\rm t}] \begin{bmatrix} X \\ Y \\ 0 \\ 1 \end{bmatrix} = K[r_1\ r_2\ {\rm t}] \begin{bmatrix} X \\ Y \\ 1 \end{bmatrix} = {\rm H} \begin{bmatrix} X \\ Y \\ 1 \end{bmatrix}
•
Z=0Z=0 인 3D Real Coordinate 로부터 Image Plane 으로의 projection 은 위와 같이 나타낼 수 있음.
◦
즉, 3D 상의 Scene Plane 상의 점들과 2D Image Plane 사이의 변환은 Non-Singular 3×33\times 3 matrix 이기 때문에 Homography 임.
•
아래와 같은 이미지에서 전광판은 3D Scene Plane 이며, 이미지의 상에서 전광판의 네 Corner 를 기준으로 Homography 를 계산하여 이미지를 교체할 수 있음.

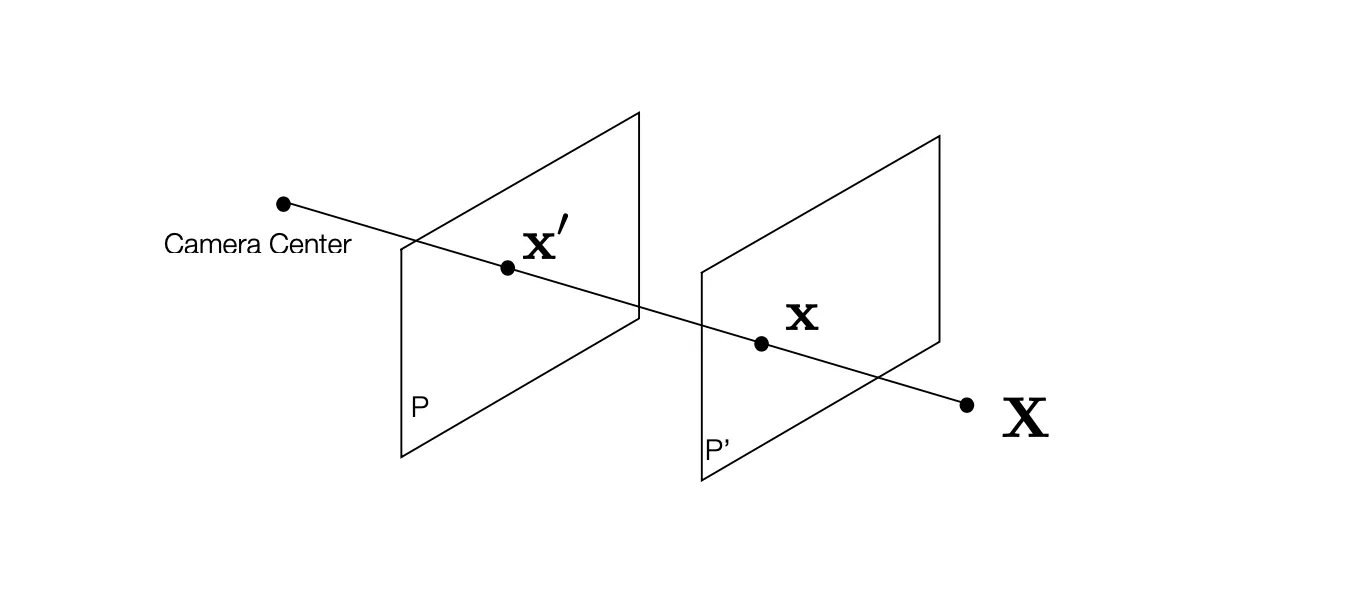
Cameras Sharing the Same Center

•
Camera Center 가 동일하고 Image Plane 이 다른 경우에 한 Image Plane 에서 다른 Image Plane 으로의 변환을 고려할 수 있음.
•
K,R,K′,R′K,R,K',R' 만을 이용해서 또 다른 Non-Singular 3×33\times3 matrix 인 Homography 를 형성할 수 있고, 이를 이용해서 변환이 가능함.
P=KR[I∣−Cworld]P′=K′R′[I∣−Cworld]→P′=K′R′(KR)−1P→x′=P′X=K′R′(KR)−1PX=K′R′(KR)−1x\begin{align*} &{\rm P} = KR[I | -{\rm C_{world}}] \\ &{\rm P}' = K'R'[I | -{\rm C_{world}}] \\ \to & {\rm P'}=K'R'(KR)^{-1}{\rm P} \\ \to & {\rm x'} = P'X = K'R'(KR)^{-1}PX = K'R'(KR)^{-1}{\rm x} \end{align*}

Moving the Image Plane with the Same Center

•
다른 모든 세팅이 동일하고 Focal Length 만 변하는 경우 (KK 만 변경) 에 한 Image Plane 에서 다른 Image Plane 으로의 변환을 고려할 수 있음.
•
K,K′K, K' 만을 이용해서 또 다른 Non-Singular 3×33\times3 matrix 인 Homography 를 형성할 수 있고, 이를 이용해서 변환이 가능함.
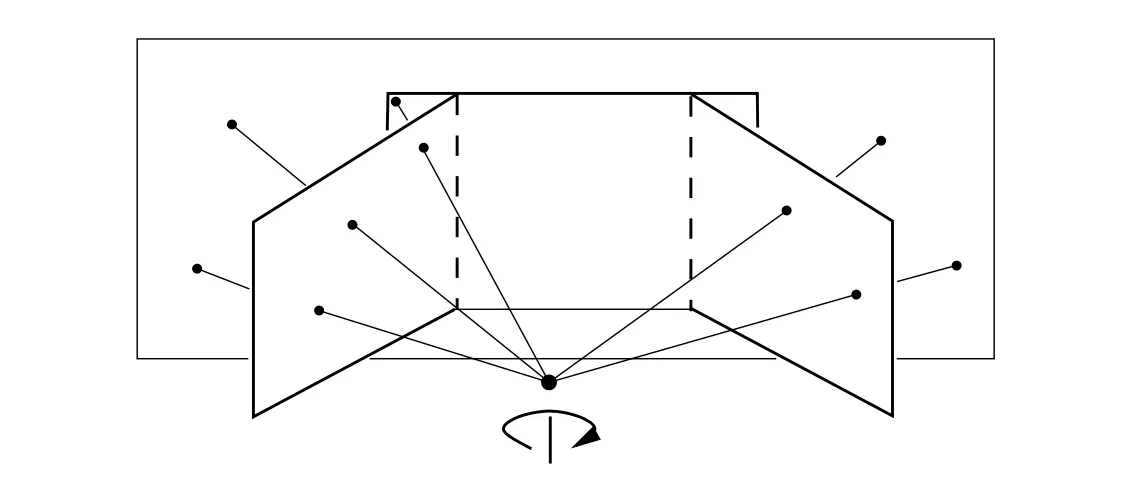
P=K[I∣0]→x=P′XP′=K′[I∣0]→x′=P′X→x′=P′X=K′K−1K[I∣0]X=K′K−1x\begin{align*} &{\rm P} = K[I | 0] \to {\rm x} =P'{\rm X}\\ &{\rm P}' = K'[I | 0] \to {\rm x'} =P'{\rm X} \\ \to &{\rm}{\rm x'} = P'X = K'K^{-1}K[I | 0]X = K'K^{-1}{\rm x} \end{align*}

Pure Camera Rotation

•
Camera Center 는 고정이고 camera 를 rotation 만 시킨 경우 한 Image Plane 에서 다른 Image Plane 으로의 변환을 고려할 수 있음.
•
K,RK,R 만을 이용해서 또 다른 Non-Singular 3×33\times3 matrix 인 Homography 를 형성할 수 있고, 이를 이 용해서 변환이 가능함.
P=K[I∣0]→x=P′XP′=K[R∣0]→x′=P′X→x′=P′X=KR[I∣0]X=KRK−1K[I∣0]X=KRK−1x\begin{align*} &{\rm P} = K[I | 0] \to {\rm x} =P'{\rm X}\\ &{\rm P}' = K[R | 0] \to {\rm x'} =P'{\rm X} \\ \to &{\rm}{\rm x'} = P'{\rm X} = KR[I | 0]{\rm X}= KRK^{-1}K[I | 0] {\rm X} = KRK^{-1}{\rm x} \end{align*}

Camera Sharing the Same Center: Summary

•
Camera Sharing Same Center 의 구체적인 예시로는 Focal Length 변화나 Pure Rotation 등이 있음.
•
3D Structure 에 대한 고려를 할 필요 없이 3×33\times 3 Homography 로 변환이 가능함.

Motion Parallax

•
Camera Center 의 위치에 따라서 동일한 점으로 projection 되었던 두 점이 분리될 수 있음.
◦
이 상대적인 분리의 displacement 를 Motion Parallax 라고 함.
•
위 그림에서 컵과 그림은 교점이 생기는 형태가 Pure Rotation 에서는 유지되었지만, Camera Center 를 변경하면 해당 형태가 사라짐.
•
즉, Camera Center 가 바뀌는 경우에는 3D Structure 에 따라서 다르게 보일 수 있음.
◦
반대로 말하면, Camera Center 를 움직이면 3D Structure 에 대한 힌트를 얻을 수 있음.

What Does Calibration (or KK) Give?

•
3D Ray 를 다음과 같이 정의할 수 있음.
X~=λd\tilde{\rm X} = \lambda {\rm d}
◦
λ\lambda 는 parameter 이고, d{\rm d} 는 ray direction 임.
•
3D Ray 상의 점을 projection 하면 다음과 같은 식을 얻을 수 있음.
x=K[I∣0](λd,1)T=Kd{\rm x} = K[I | 0](\lambda {\rm d}, 1)^T = K {\rm d}
◦
Up-to-Scale 이기 때문에 λ\lambda 항이 사라짐.
•
Intrinsic Parameter KK 를 알면, Projected Point 로부터 3D Ray 를 다시 얻어낼 수 있음.
d=K−1x{\rm d} = K^{-1}{\rm x}
•
이를 이용해 두 3D Ray 가 이루는 각도를 다음과 같이 구해낼 수 있음.
cos⁡θ=d1Td2d1Td1d2Td2=(K−1x1)T(K−1x2)(K−1x1)T(K−1x1)(K−1x2)T(K−1x2)=x1T(K−TK−1)x2x1T(K−TK−1)x1x2T(K−TK−1)x2=x1Tωx2x1Tωx1x2Tωx2\begin{align*} \cos\theta &= \frac{{{\rm d_1}^T{\rm d_2}}}{\sqrt{{\rm d_1}^T{\rm d_1}}\sqrt{{\rm d_2}^T{\rm d_2}}} = \frac{{(K^{-1}{\rm x_1})^T(K^{-1}{\rm x_2})}}{\sqrt{(K^{-1}{\rm x_1})^T(K^{-1}{\rm x_1})}\sqrt{(K^{-1}{\rm x_2})^T(K^{-1}{\rm x_2})}} \\ &= \frac{{\rm x_1}^T(K^{-T}K^{-1}){\rm x_2}}{\sqrt{{\rm x}_1^T(K^{-T}K^{-1}){\rm x_1}}{\sqrt{{\rm x}_2^T(K^{-T}K^{-1}){\rm x_2}}}} = \frac{{{\rm x_1}^T\omega{\rm x_2}}}{\sqrt{{\rm x_1}^T\omega{\rm x_1}}\sqrt{{\rm x_2}^T\omega{\rm x_2}}} \end{align*}
◦
ω=K−TK−1\omega = K^{-T}K^{-1}
◦
Orthogonal Ray 의 경우에는 x1Tωx2=0{\rm x_1}^T\omega {\rm x_2} = 0 임을 알 수 있음.
▪
역으로, Calibration 을 할 때 (KK 를 찾고자 할 때) 이 방법을 사용할 수 있음.

The Image of The Absolute Conic

•
Plane at Infinity π∞\pi_{\infty} 위의 점 X∞{\rm X}_{\infty} 는 Ideal Point 이기 떄문에 다음과 같이 표현할 수 있음.
X∞=(dT,0)T{\rm X}_{\infty} = ({\rm d}^T, 0)^T
•
X∞{\rm X}_{\infty} 를 projection 하면 다음과 같은 식을 얻어낼 수 있음.
x=PX∞=KR[I∣−C~](d0)=KRd{\rm x}= {\rm P}{\rm X}_{\infty} = KR[I | -{\rm \tilde C}] \begin{pmatrix} {\rm d} \\ 0 \end{pmatrix} = KR{\rm d}
◦
Ideal Point 의 projection 은 Camera Center 에 무관함을 알 수 있음.
◦
KRKR 은 Non-Singular 3×33\times3 matrix 이므로 Homography 고 H{\rm H} 라 할 수 있음.
•
Point 에 대한 Homography 가 H{\rm H} 일 때 Conic 의 변환은 C→H−TCH−1C \to {\rm H}^{-T}C{\rm H}^{-1} 이었고, Absolute Conic 에 대한 C=IC = I 이며 Absolute Conic 의 각 점은 Ideal Point 이기 때문에 Absolute Conic 의 상은 다음과 같이 표현됨.
ω=(KR)−TI(KR)−1=K−TRR−1K−1=(KKT)−1\omega = (KR)^{-T}I(KR)^{-1} = K^{-T}RR^{-1}K^{-1} = (KK^T)^{-1}
•
Image of Absolute Conic (IAC) 의 표현인 ω\omega 는 앞선 두 3D Ray 의 각을 산출할 때 필요한 요소였음.
◦
Orthogonal Ray 를 찾으면 x1Tωx2=0{\rm x_1}^T \omega {\rm x_2} = 0 식이 성립하고, 이를 만족하는 point 여러 개를 찾아 DLT 를 진행하여 ω\omega 를 구한 뒤에 Cholesky Decomposition 을 행하면 최종적으로 KK 를 얻을 수 있음!
◦
ω=(KK−T)−1\omega = (KK^{-T})^{-1} 은 6DoF (Symmetric Matrix) - 1DoF (Up-to-Scale) = 5DoF 를 가지기 때문에, DLT 를 통해 구해내기 위해서는 5 개의 Corresponding Point 가 필요함.
▪
근데, 90°90\degree 를 이루는 3D Ray 위의 Point 5 개를 찾기는 굉장히 어렵기 때문에 실제 유용하진 않음.
▪
Zhang’s Method 에서 나왔던 B{\rm B} 항목이 IAC ω\omega 와 동일하기에 해당 방법론으로 진행한다면 Calibration 에 3 Corresponding Points 가 필요함.

The Image of The Absolute Conic: Remark

•
Plane π\pi 는 Plane at Infinity π∞\pi_{\infty} 와 선에서 만나는데, 이 선은 Absolute Conic Ω∞\Omega_{\infty} 와 π\pi 의 Circular Points 에서 만나게 됨.
•
Image of Absolute Conic ω\omega 는 Image of Circular Points 를 포함함.

A Simple Calibration Device

•
형태를 아는 물체를 준비하고, 캡처한 뒤에 Homohraphy H{\rm H} 를 계산할 수 있음. (Planar to Image)
H=[h1,h2,h3]{\rm H} = [h_1, h_2, h_3]
•
Planar 에서의 Circular Point 의 이미지에서의 대응점은 Homography 를 적용하면 되고, 다음과 같이 표현할 수 있음.
H(1,±i,0)T→h1±ih2{\rm H}(1, \pm i, 0)^T \to h_1 \pm ih_2
•
Circular Point 의 상은 IAC ω\omega 위에 있으므로, 다음이 성립함.
(h1±ih2)Tω(h1±ih2)=0h1Tωh2=0h1Tωh1=h2Tωh2=0(h_1 \pm ih_2)^T\omega (h_1 \pm ih_2) = 0 \\ {\rm h_1}^T\omega {\rm h_2} = 0 \quad {\rm h_1}^T\omega {\rm h_1} ={\rm h_2}^T\omega {\rm h_2} = 0
◦
Zhang’s Method 에서는 Z=0Z=0 의 특수한 경우에서 Homography H{\rm H} 와 rotation matrix 의 column vector 의 관계를 바탕으로 calibration 을 했다면, 지금은 Absolute Conic 과 Circular Point 의 관계를 바탕으로 calibration 을 함.
◦
결과적으로는 Zhang’s Method 와 동일한 식이 나옴. → 5DoF, 한 Homography 당 2DoF 충족
•
만약 형태를 아는 물체가 3개정도 있어서 서로 다른 Homography 를 3개 구할 수 있을 경우 DLT 를 통해 Sigle Image Calibration 이 가능하게 됨.

Calibration via Orthogonal Vanishing Points

•
Square Pixel 이라는 가정이 존재하면 KK 에서 αx=αy\alpha_x = \alpha_y 이고, 기존의 ω\omega 가 3DoF 로 바뀜.
ω=(KKT)−1=[w10w20w1w3w2w3w4]→3DoF (Up-to-Scale)\omega = (KK^T)^{-1} = \begin{bmatrix} w_1 & 0 & w_2 \\ 0 & w_1 & w_3 \\ w_2 & w_3 & w_4 \end{bmatrix} \to \rm{3 DoF}\ (Up{\text -} to{\text -}Scale)
•
3 개의 Orthogonal Axis 가 이미지 내에서 존재하면, 세 쌍의 90°90\degree 를 이루는 점들을 찾을 수 있고 이들 점들은 다음과 같은 수식을 만족함을 이전에 보임.
viTωvj=0{\rm v_i}^T \omega {\rm v_j} = 0
•
결국, 3DoF 인 ω\omega 와 세 쌍의 점들 (vi,vj)({\rm v}_i, {\rm v}_j) 이 존재하여 ω\omega 를 온전히 구해낼 수 있고 Single Image Calibration 이 가능함.

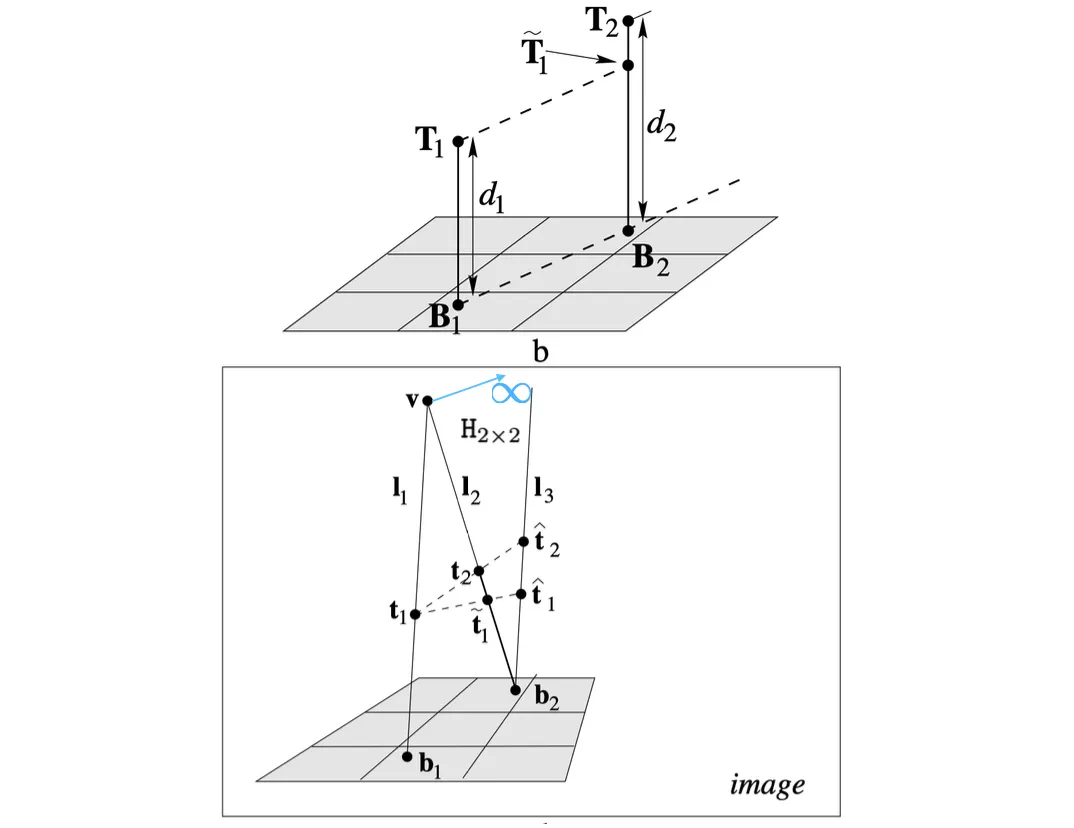
Measuring Height from a Single Image

•
Parallel Line 이 Vanishing Line 위의 점에서 만난다는 점을 이용해 실질적인 Height Ratio 를 비교할 수 있음.
•
원하는 평행한 (서 있는) 두 물체 (l1,l2)(\rm l_1, l_2) 의 밑 부분을 각각 b1,b2{\rm b_1, b_2} 라고 하고, Vanishing Line 을 l{\rm l} 이라고 하면, b1,b2{\rm b_1, b_2} 를 이은 선과 Vanishing Line 의 교점은 다음과 같음.
u=(b1×b2)×lu = ({\rm b_1}\times {\rm b_2})\times {\rm l}
•
b1,b2{\rm b_1, b_2} 를 이은 직선과 평행한 직선은 동일하게 uu 에서 만나야 하므로, 한 물체 (l1)(\rm l_1) 의 꼭대기 t1t_1 과 uu 를 이은 직선과 다른 물체 (l2)({\rm l}_2) 와 만나는 점인 t~1\tilde{t}_1은 동일한 높이를 가지는 지점임.
t~1=(t1×u)×l2\tilde{t}_1 = (t_1 \times u) \times {\rm l}_2
•
이렇게 t~1\tilde{t}_1 을 구하면, b2,t~1,t2{\rm b}_2, \tilde{t}_1, t_2 는 한직선에 있고 두 물체가 평행하게 서 있으므로 두 물체가 나타내는 직선의 교점을 vv 라고 하면, 이 vv 또한 앞선 세 점과 같은 직선 상에 있으며 Ideal Point 가 됨.
v=l1×l2v={\rm l_1}\times{\rm l_2}
•
궁금한 것은 b2t~1{\rm b}_2\tilde{t}_1 의 길이와 (물체 1의 길이) b2t2{\rm b}_2 t_2 의 길이 (물체 2의 길이) 의 비율인데, Affine Transform 은 Length Ratio 를 유지하므로 다음의 mapping 을 시켜주는 1D Transform 을 통해 실제 평행한 두 선을 평행하여 (v→∞v \to \infty 로 가도록) 만나지 않도록 변경할 수 있음. (실제 3D 에선 만나지 않기 때문임.)
(0,1)→(0,1)&(v,1)→(1,0)→H2×2=[101−v](0,1) \to (0,1)\quad \& \quad (v,1) \to (1,0) \\ \to {\rm H}_{2\times 2} = \begin{bmatrix} 1 & 0 \\ 1 & -v \end{bmatrix}
•
해당 transform 을 적용하면 t~1\tilde{t}_1 과 t2t_2 는 다음과 같이 변형됨.
T~1=H2×2[t~11]=[t~1t~1−v]=[t~1t~1−v1]T~2=H2×2[t21]=[t2t2−v1]\tilde{T}_1 = {\rm H}_{2\times 2} \begin{bmatrix} \tilde{t}_1 \\ 1 \end{bmatrix} = \begin{bmatrix} \tilde{t}_1 \\ \tilde{t}_1 - v \end{bmatrix} = \begin{bmatrix} \frac{\tilde{t}_1}{\tilde{t}_1 - v} \\ 1 \end{bmatrix} \\ \tilde{T}_2 = {\rm H}_{2\times 2} \begin{bmatrix} {t}_2 \\ 1 \end{bmatrix} = \begin{bmatrix} \frac{{t}_2}{{t}_2 - v} \\ 1 \end{bmatrix}
•
즉 위 식을 이용해서 최종적인 Length Ratio 는 다음과 같이 계산할 수 있음.
d1d2=T~1T~2=t~1(t2−v)t2(t~1−v)\frac{d_1}{d_2} = \frac{\tilde{T}_1}{\tilde{T}_2}= \frac{\tilde{t}_1(t_2-v)}{t_2(\tilde{t}_1 -v)}