Duplicate

Lecture 6 | Hough Transformation

수강 일자
2022/09/26

Preprocessing Edge Images

•
Hough Transformation: Noisy 하거나 끊긴 edge 가 detection 되었을 때, 그것으로부터 line, circle, object 들을 찾아낼 수 있는 알고리즘

Hough Transformation

•
Binary Structure (Edge 인지 아닌지 명시한 이미지) 로 부터 어떠한 구조를 탐지해내는 방법론
◦
Edge 가 완벽히 연결되어 있지 않아도 동작함.
◦
Structure 가 occlusion 에 이해서 완전히 보이지 않아도 동작함.
◦
단일이 아닌 다중 구조 (ex. line, circle) 를 탐지해낼 수 있음.

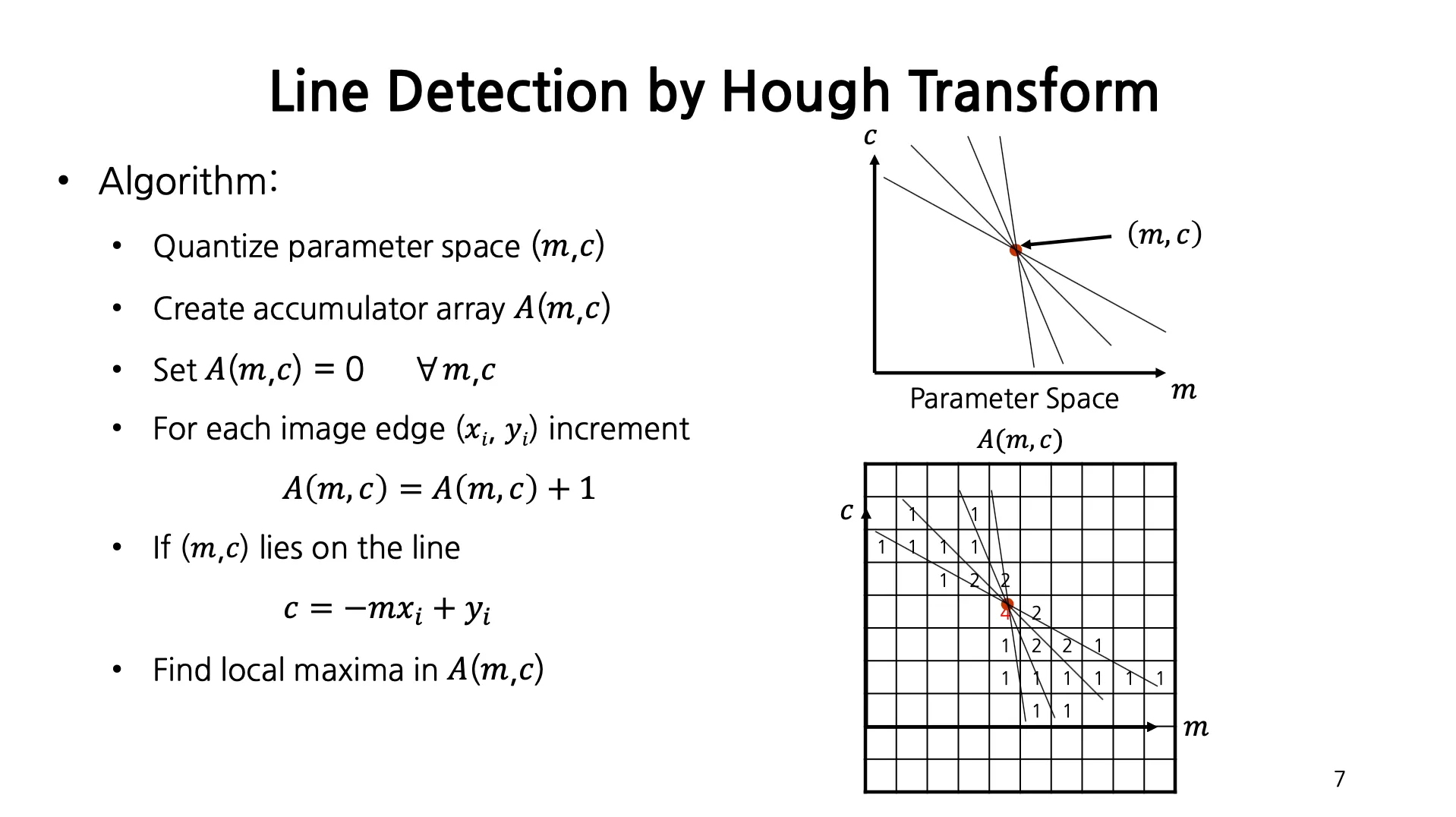
Line Detection by Hough Transform

•
주어진 데이터 좌표들을 잘 표현하는 y=mx+cy=mx+c 의 mm 과 cc 를 찾는 문제를 가정함.
•
parameter 인 mm 과 cc 로 이루어진 공간을 Hough Space 라고 함.
•
Image Space 에서 점 하나가 Parameter Space (Hough Space) 에서 선 하나에 대응됨.
◦
yi=mxi+c→c=−mxi+yiy_i=mx_i+c \rarr c= -mx_i+ y_i
◦
c=−m+2c = -m +2
◦
c=−3m+4c = -3m+4
◦
c=−5m+6c=-5m +6
◦
c=−7m+8c=-7m +8
◦
4 개의 점이 공통적으로 지나는 점인 m=1m=1, c=1c=1 로 parameter 를 찾게 됨.
•
Algorithm 은 다음과 같음.
1.
찾고자 하는 parameter mm, cc 의 Hough Space 를 정의하고 해당 영역을 discrete 하게 나눔.
2.
나눠진 각각의 영역을 Accumulator Array A(m,c)A(m,c) 로 정의하고, 이를 0 으로 초기화함.
3.
각각의 Image Point (xi,yi)(x_i, y_i) 에 대해서 해당 Point 로 구해낸 mm, cc 에 대한 line 을 discrete 영역에 그리고 해당 line 이 통과하는 영역에 1 을 더함.
4.
Accumulator Array 의 Local Maxima 를 찾으면 해당 mm, cc 에 해당하는 line 을 통과하는 Image Point 가 많이 존재했다는 것임.

Better Parameterization (Line Detection)

•
mm 이 가질 수 있는 범위가 −∞≤m≤∞-\infty \le m \le \infty 이기 때문에 이러한 parameterization 은 memory 나 computation 측면에서 좋지 못함.
•
ρ=xcos⁡θ+ysin⁡θ\rho = x\cos \theta + y\sin \theta
◦
ρ\rho 는 원점에서 선까지의 최단거리 (수직 거리)
◦
θ\theta 는 최단거리 선과 xx 축과의 각도
◦
두 parameter 를 0≤θ≤2π0 \le \theta \le 2\pi, 0≤ρ≤ρmax⁡0\le \rho \le \rho_{\max} 로 범위를 제한 할 수 있음. (ρmax⁡\rho_{\max} 는 이미지 크기가 정해져 있기 때문에 bounding 가능!)
◦
y=mx+c→y=−cos⁡θsin⁡θx+ρsin⁡θy=mx+c \rarr y = -\frac{\cos\theta}{\sin\theta}x + \frac{\rho}{\sin\theta}
◦
Image Space 에서의 (xi,yi)(x_i, y_i) 는 Hough Space 에서 ρ=xicos⁡θ+yisin⁡θ\rho=x_i\cos\theta + y_i\sin\theta 의 sinusoid 에 대응됨.

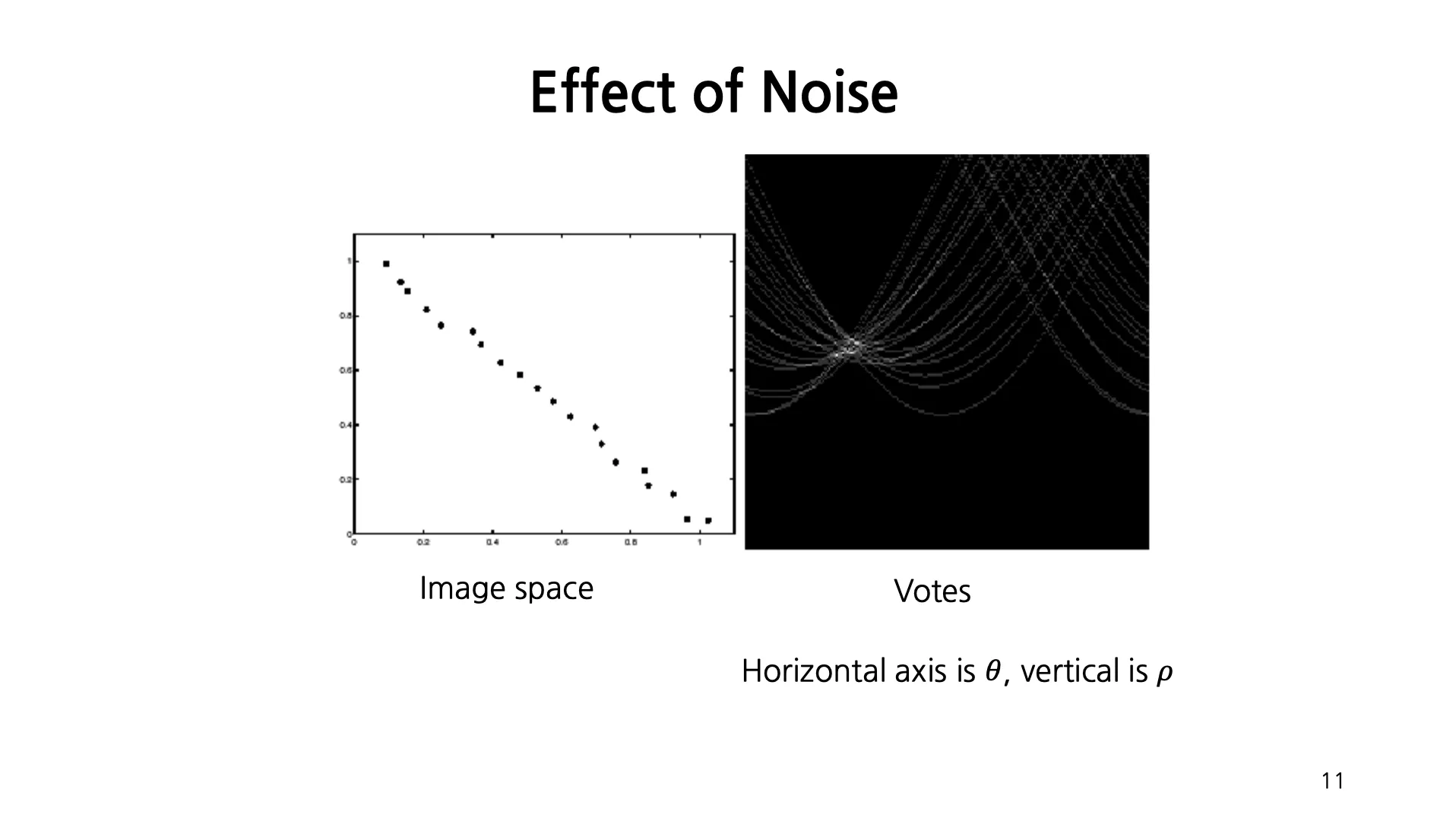
Effect of Noise

•
Voting Point 가 하나로 결정되지 않고 영역에서 퍼져있음. → noise 애 취약
•
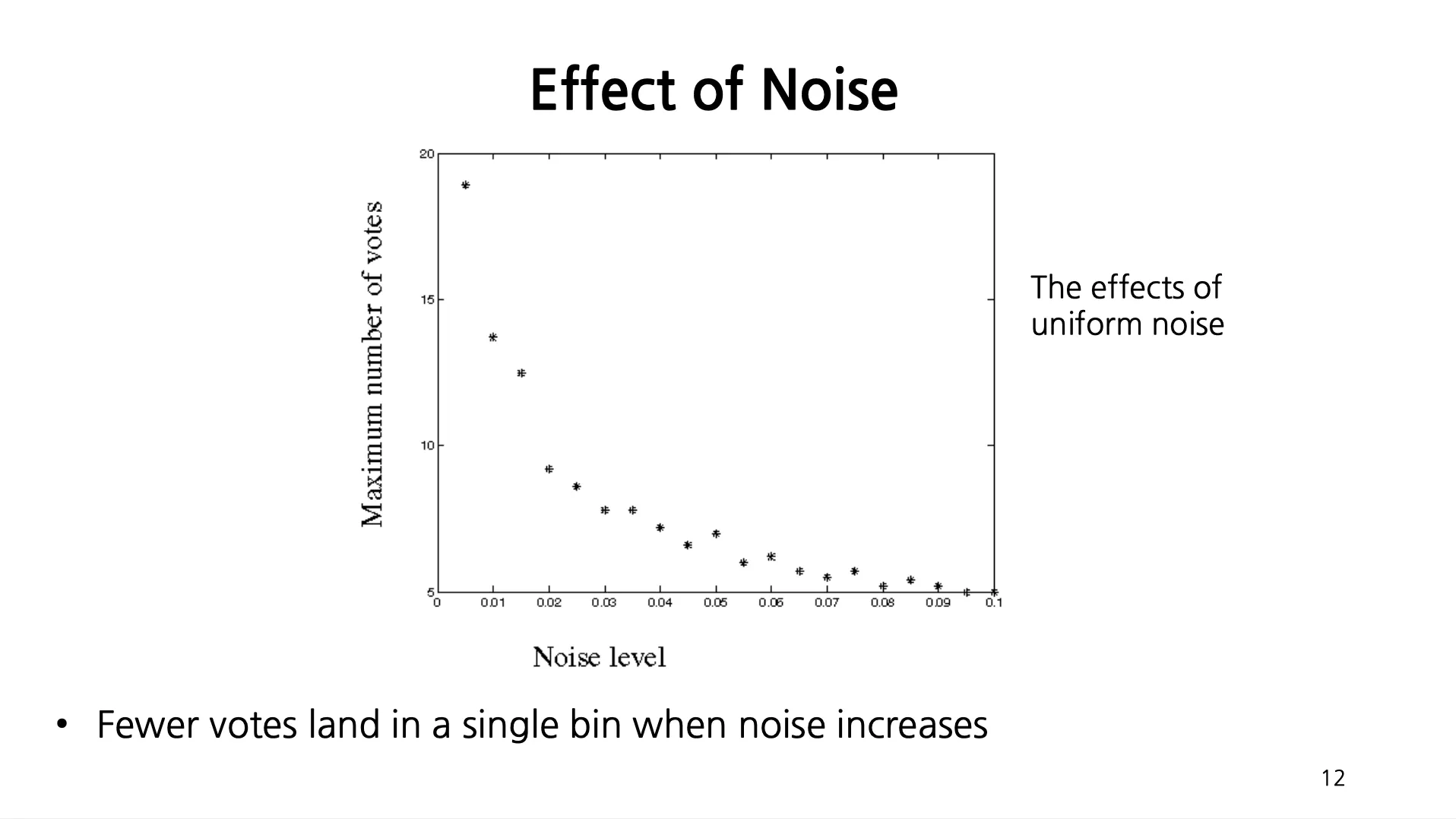
Noise 레벨이 크면 Maximum number of votes 가 급격히 감소함.

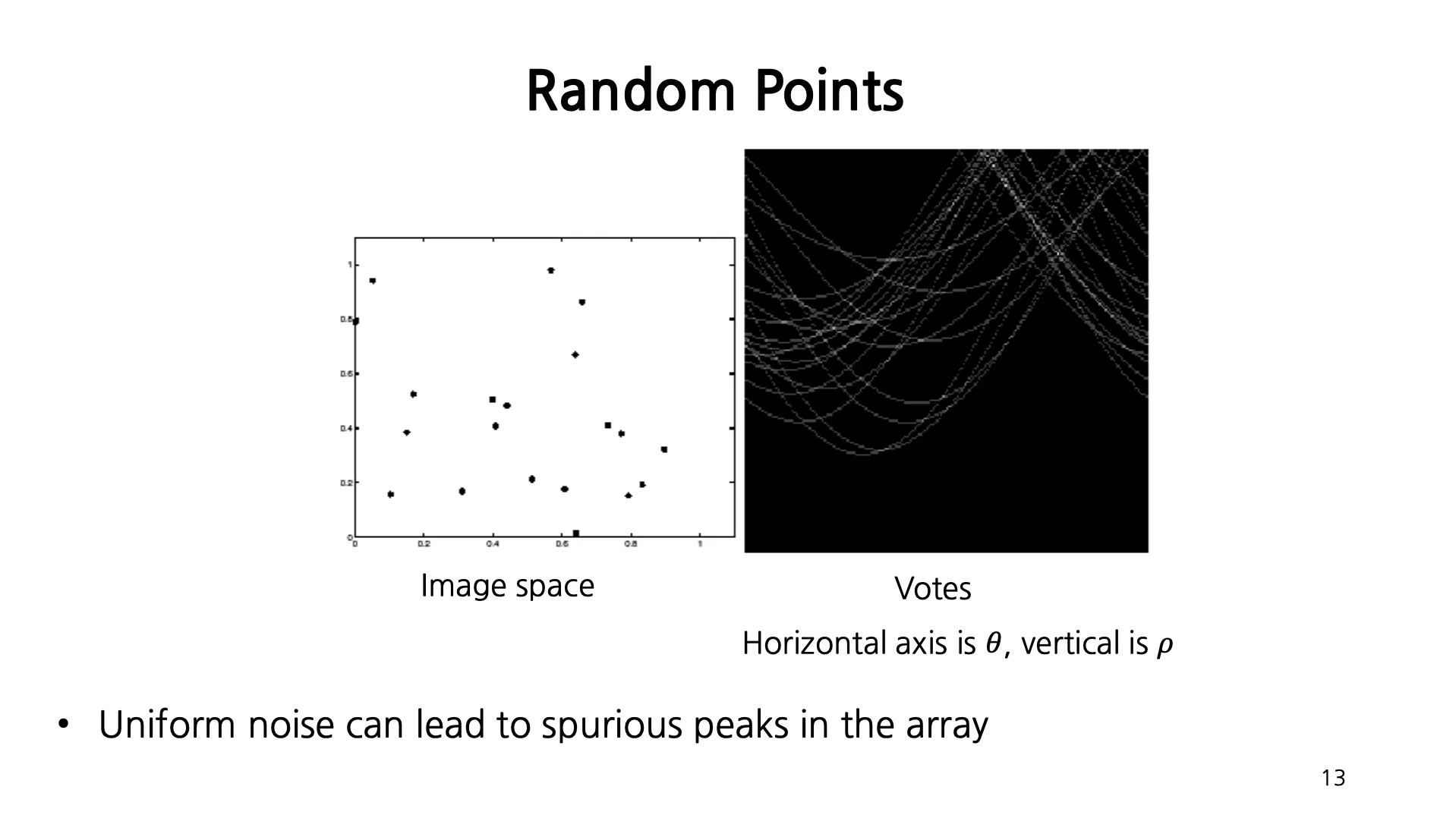
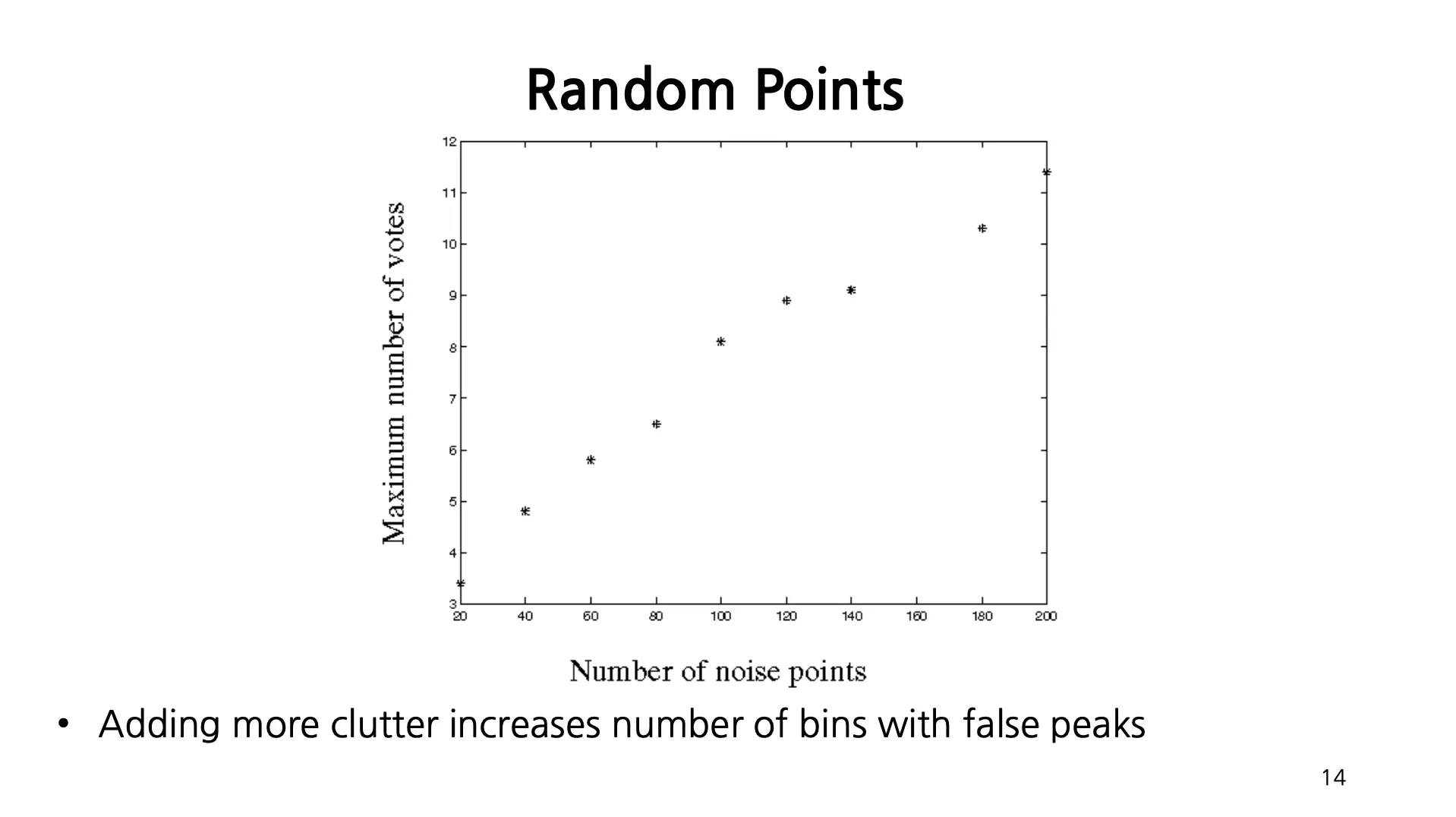
Random Points

•
Uniform Noise 는 Accumulator Array 상에서 그럴싸한 가짜 peak 를 만들어 낼 수 있음.
•
Random Points 의 수를 증가시키면 Maximum nuber of votes 도 따라서 증가함.
◦
Background 에 잡다한 잡음을 넣는 것은 가짜 peak (line) 을 생기게 함.

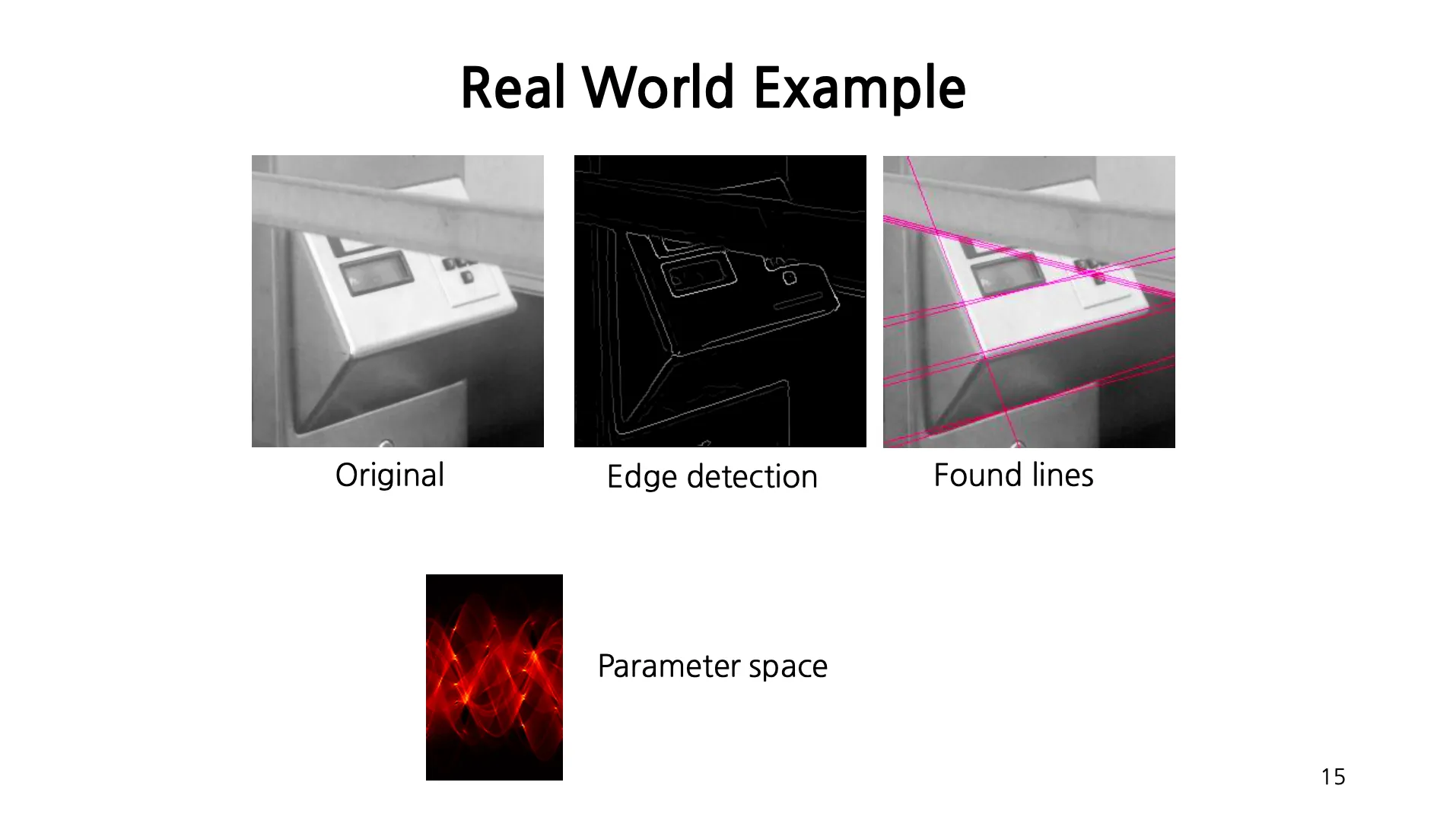
Real World Example

Mechanics of the Hough Transform

•
얼마나 많은 Line 을 detect 할 건지는 threshold 로 결정할 수 있음. (몇 이상의 값을 가지는 Accumulator Array 를 line 으로 볼 것인지)
•
Local Maxima 가 가까운 영역에서 붙어있는 경우, 하나로 취급할 수도 있음.
•
어떤 점들이 어떤 line 에 대응되는지는 detect 한 line 과 점과의 거리를 통해 알 수 있음.
•
ρ\rho, θ\theta 로 이루어진 Hough Space 상에서 Accumulator Array 를 정의하기 위해서 discrete 하게 나눌 때 얼마나 촘촘하게 나눌지에 대한 여부?
◦
너무 간격이 넓게 나눌 경우: 다른 두 개의 선을 합쳐버릴 수도 있음.
◦
너무 간격이 좁게 나눌 경우: Threshold 를 넘는 칸이 없어 선을 찾을 수 없을 수도 있음.
•
Hough Transformation 의 장점
◦
선이 끊기거나 가려져 있어도 찾을 수 있음.
◦
한 번의 알고리즘 시행으로 여러 개의 선을 한 번에 찾을 수 있음
◦
어느정도의 noise 에 대해서는 robust 함. (칸에만 들어있으면 카운팅이 되므로)
•
Hough Transformation 의 단점
◦
모델의 parameter 의 개수에 따라서 Hough Space 의 차원이 늘어나기 때문에 Time Complexity 가 exponential 하게 증가함.
◦
Random noise 에 의해서 그럴듯한 가짜 peak 선들이 나타날 수 있음.
◦
Accumulator Array size 를 정하기 쉽지 않음.

Finding Circles by Hough Transform

•
원의 방정식: (xi−a)2+(yi−b)2=r2(x_i-a)^2 + (y_i-b)^2 = r^2
•
Parameter 는 rr, aa, bb 로 세 가지 종류이지만, 논의의 간략화를 위해 rr 을 고정함.
◦
xix_i, yiy_i 가 주어졌을 때 aa, bb 를 축으로 하는 Hough Space 에서의 식은 원 형태가 됨.
◦
(a−xi)2+(b−yi)2=r2(a-x_i)^2 + (b-y_i)^2 = r^2
◦
Hough Space 에서 원의 교차점으로 parameter aa, bb 를 찾게 됨.
•
rr 을 고정하지 않은 경우는 parameter 가 rr, aa, bb 로 3 개가 됨.
◦
Accumulator Array A(a,b,r)A(a,b,r) 은 3 차원에 정의됨.
◦
rr 이 고정되면 abab plane 에서 원이므로, rr 이 바뀌면 그에 따라 원의 반지름이 달라지는 원뿔이 됨.
◦
원뿔의 겉면 (surface) 에 해당하는 모든 영역에 Accumulator Array 의 값을 +1 해주어야 함.

Using Gradient Information

•
Edge 와 수직인 gradient direction 을 활용하여 Accumulator Array 의 computation cost 를 줄일 수 있음.
◦
Edge location: (xi,yi)(x_i,y_i)
◦
Edge direction: ϕ\phi
◦
a=x−rcos⁡ϕa = x-r\cos\phi
◦
b=y−rsin⁡ϕb=y-r\sin\phi
•
xx, yy, ϕ\phi, rr 를 정확히 알면 한 점에 대해서 (a,b)(a,b) 가 유일하게 결정됨. → Accumulating 을 하는 point 가 한 지점 뿐임. 한 지점이 아니라 주변만 voting 한다고 하더라도 computation cost 가 많이 감소함.

Finding Coins

•
radius 에 대한 사전 정보가 있을 때 abab plane 에서의 후보 circle 들의 모습임.

Generalized Hough Transform

•
선이나 원처럼 사전에 정의된 형태만 찾는 것이 아니라 임의의 형태를 찾는 Hough Transform.
•
임의의 물체에 대한 형태를 찾는 거라기 보다는 center, scale, rotation 을 찾음.
◦
xcx_c, ycy_c → center
◦
ss → scale
◦
θ\theta → rotation
◦
다만 이렇게 parameter 가 4 개이면 4 차원 공간의 Hough Space 가 나오기 때문에 복잡함.
•
먼저 Object Center (xc,yc)(x_c, y_c) 를 찾는 경우만을 고려함.
1.
Reference Point (x0,y0)(x_0, y_0) 을 center 처럼 보이는 곳으로 대충 정함.
2.
각각의 edge point (xi,yi)(x_i,y_i) 에 대해서 (ri,αi,ϕi)(r_i, \alpha_i, \phi_i) 를 구함.
•
r⃗\vec{r} : boundary point 으로부터 reference point 까지의 거리벡터 r⃗=(ri,αi)\vec{r} = (r_i, \alpha_i)
◦
αi\alpha_i 는 xx 축과의 각도
•
ϕi\phi_i: gradient 방향 각도 (xx 축과의 각도)
3.
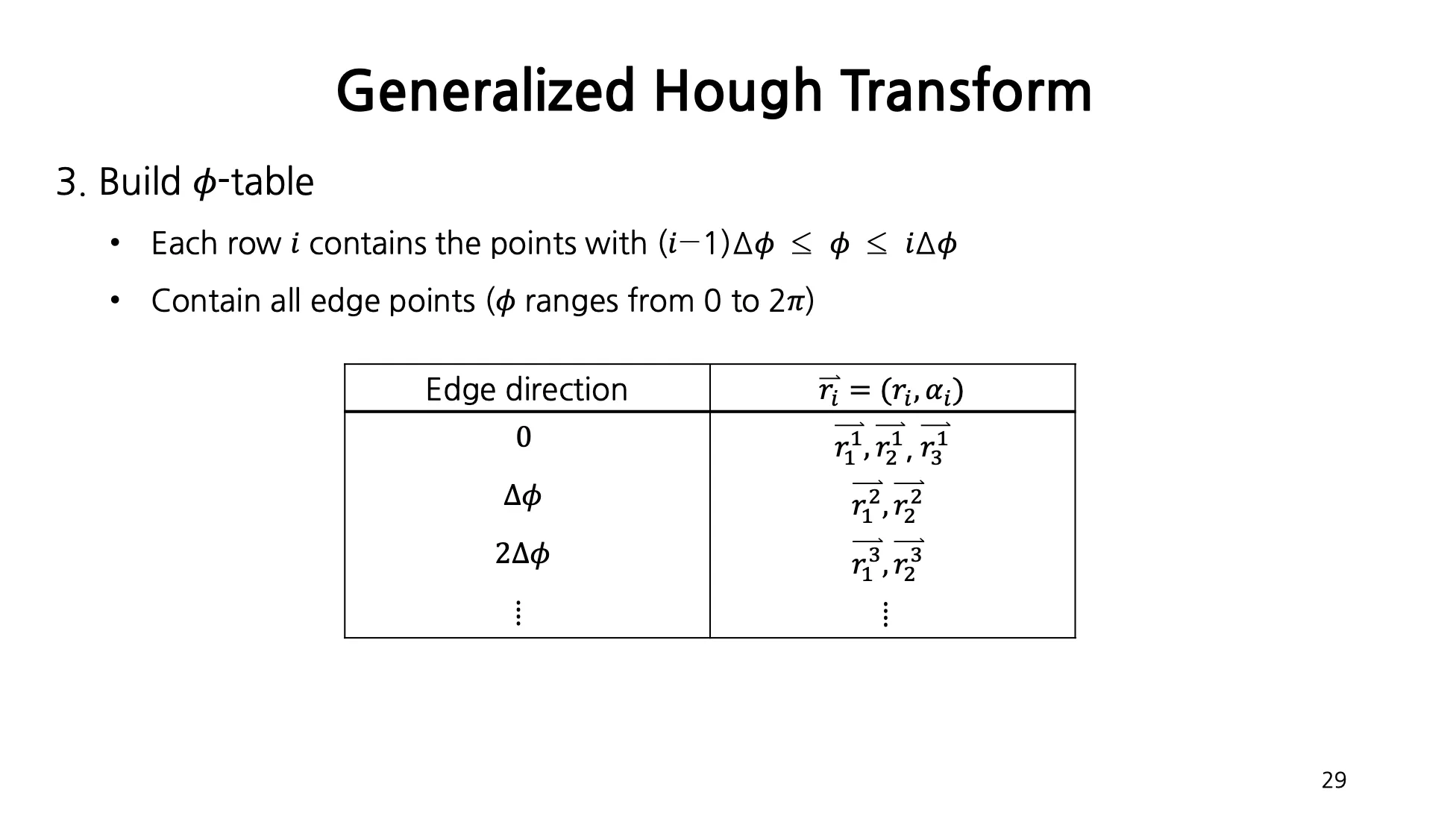
ϕ\phi - table 을 만듬.
•
테이블 간격인 △ϕ\triangle\phi 를 정의하고 각 간격 범위인 (i−1)△ϕ≤ϕ≤i△ϕ(i-1)\triangle\phi \le \phi \le i\triangle\phi 에 속하는 점들을 적음. (ri,αir_i, \alpha_i 를 적음)
•
위를 00 부터 2π2\pi 까지 진행함.
4.
중심점을 찾는 Accumulator Array A(x,y)A(x,y) 를 정의하고 0 으로 초기화함.
•
xc,min⁡≤xc≤xc,max⁡x_{c,\min} \le x_c \le x_{c, \max}
•
yc,min⁡≤yc≤yc,max⁡y_{c,\min} \le y_c \le y_{c, \max}
5.
각각의 edge point (xi,yi)(x_i,y_i) 에 대해서 본인이 속한 Edge direction entry 에 속한 모든 점들에 대해서 다음과 같이 x,yx, y 를 구함.
•
x=xi+rkicos⁡αkix = x_i +r_k^i \cos \alpha_k^i
•
y=yi+rkisin⁡αkiy = y_i +r_k^i \sin \alpha_k^i
6.
위에서 구해낸 xx, yy 에 대해 A(x,y)A(x,y) 에 +1 을 해줌.
•
다음으로 Scale ss 와 Rotation θ\theta 를 적용한 버전은 다음과 같음.
◦
xc=xi+rkiscos⁡(αki+θ)x_c=x_i+r_k^is\cos(\alpha_k^i + \theta)
◦
yc=yi+rkissin⁡(αki+θ)y_c=y_i+r_k^is\sin(\alpha_k^i + \theta)
◦
Computation cost 때문에 일반적으로 사용되지 않고 center 만 찾는 경우가 많음.

Examples of GHT

•
자동차의 part detector 로 바퀴를 찾으면 바퀴 기준 양 옆을 center 로 vote 할 수 있음.
•
자동차의 part detector 로 wind shield 를 찾고 기 기준으로 center 를 vote 할 수도 있음.
•
수 많은 자동차의 part 들이 공통적으로 center vote 하는 지점을 찾을 수 있음.

Implicit Shape Models: Training

•
Interest Point 라는 feature point 를 잡고 그 주변을 patch 로 선언함.
•
Patch 를 clustering 하여 cluster center 를 얻어내면 part patch 같은 것들이 탐지가 됨.
•
새로운 이미지가 왔을 때 interset point 를 찾고 그 주변의 patch 와 앞서 찾은 cluster center 랑 비교해서 (codebook 에서 찾는다- 고 함.) 비슷한 center 로 매핑할 수 있음.
•
Patch entry 에 대해서 물체의 center 가 정의 되어 있어 이를 활용해 물체의 center 를 최종적으로 찾을 수 있음. → 이를 기반으로 segmentation 까지 가능하다고 함.

Hough Transform: Comments

•
끊겨진 edge 에 대해서도 동작함.
•
Occlusion 에 insensitive 하여 잘 동작함.
•
선, 원 같은 간단한 형태에 대해서 효과적임.
•
Image Space 와 Parametric Space 간의 trade-off 가 있음.
◦
Parameteric Space 의 차원 수 증가에 따른 computaitonal cost 의 exponential 하게 증가.
◦
Parameter 가 정해지더라도 Accumulator Array 의 size 조절 문제가 있음. (sensitivity)
•
Interest point 주변의 patch 기반의 방법론을 활용하면 edge location 이 조금 부정확하더라도 center 를 잘 찾을 수 있음.