Duplicate

Lecture 23 | Neural Radiance Fields

수강 일자
2023/03/12

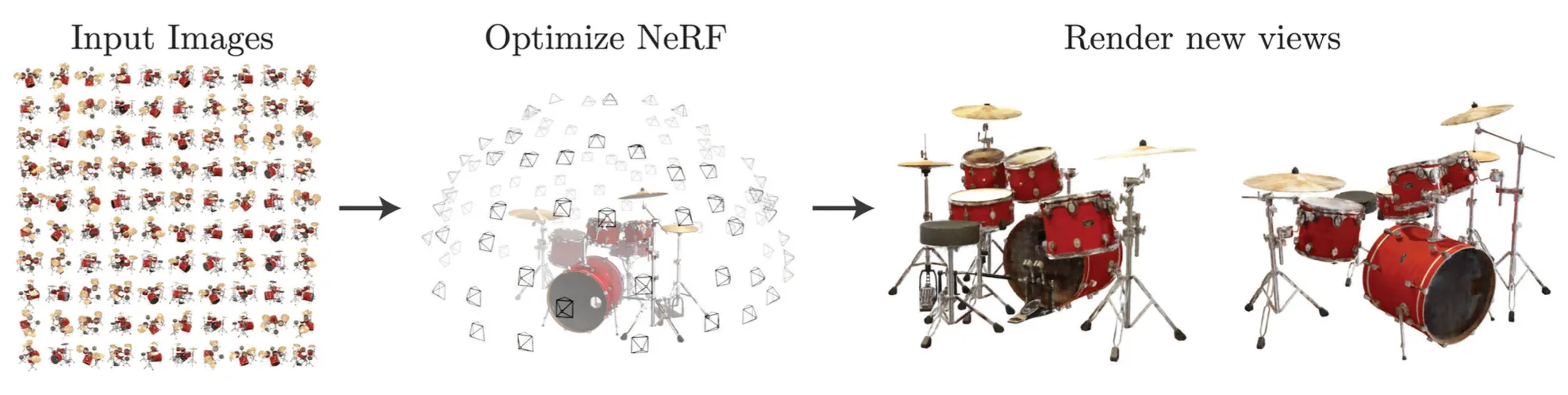
Novel View Synthesis

•
Multiview Image 와 그에 해당하는 corresponding calibration parameter 를 이용해서 Neural network 를 학습하여 임의의 viewpoint 에서의 novel view 를 만들어내는 방법론
•
large multiview image dependency, long rendering time 와 같은 단점이 있음.

NeRF: Representing Scenes as Neural Radiance Fields

•
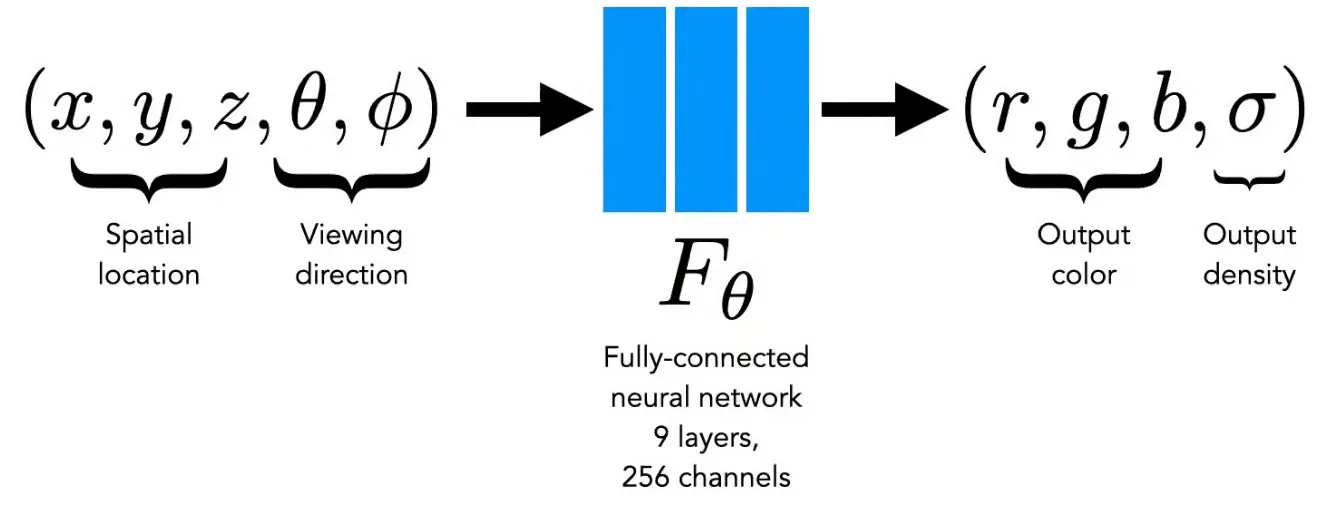
Spatial Location 과 view direction 을 입력으로 받아서 output color 와 output density 를 출력으로 내는 네트워크
◦
실제로는 view direction 이 3D vector 형태로 들어감.
•
3D Ground truth 가 존재하지 않음.
◦
이미지 단의 loss 를 활용함.
◦
3D 의 퀄리티에 영향을 받지 않음.
•
Scene 하나당 네트워크 하나가 대응됨. (memorize scene)

Volume Rendering

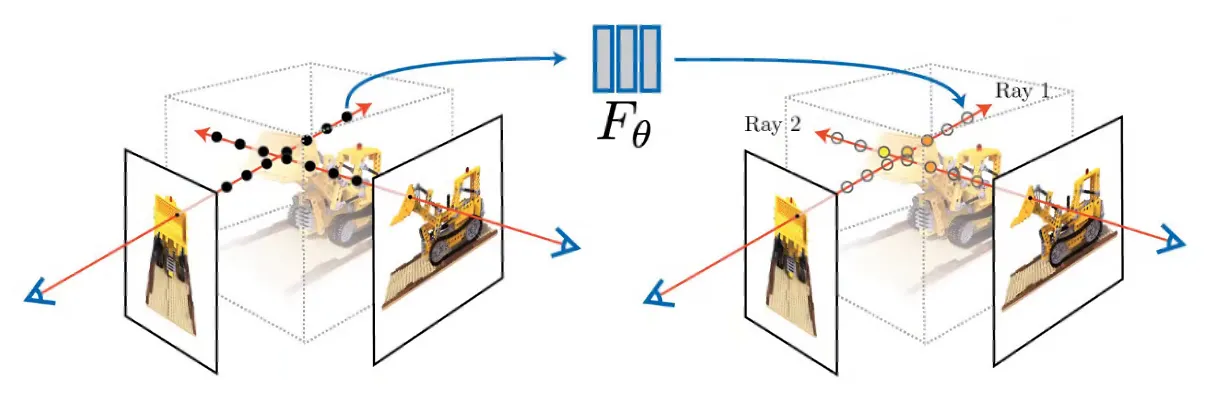
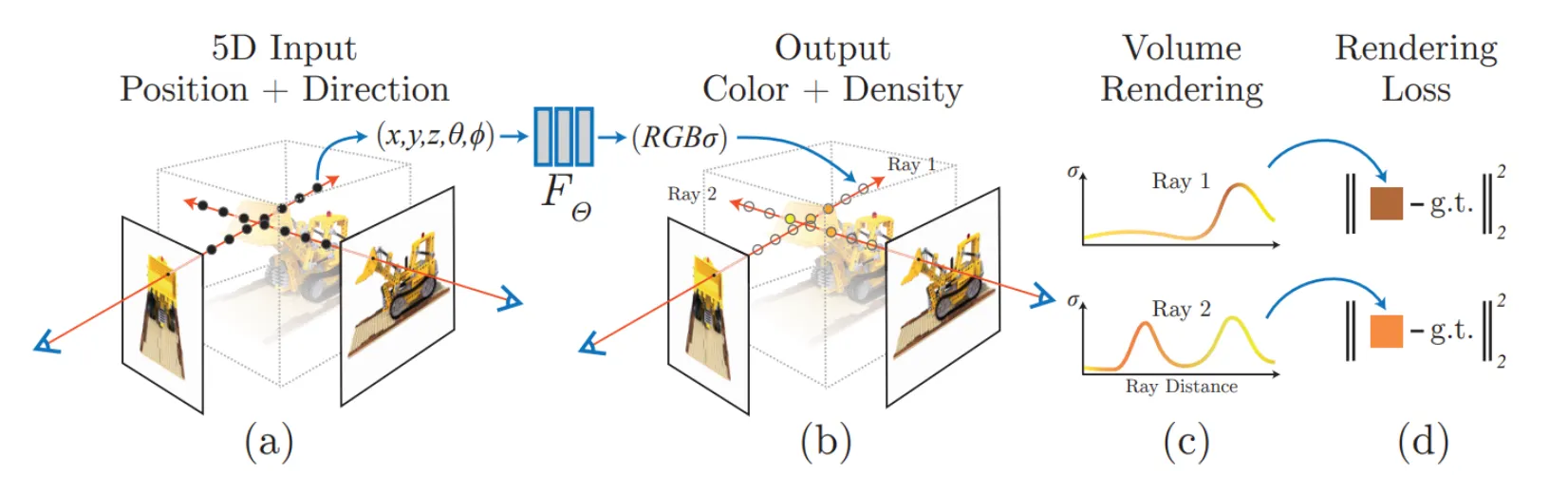
r(t)=o+tdC(r)=∫tntfT(t)σ(r(t))c(r(t),d)dt{\rm r}(t) = {\rm o} + t{\rm d} \\ C({\rm r}) = \int_{t_n}^{t_f} T(t)\sigma({\rm r}(t)){\rm c}({\rm r}(t), {\rm d})dt
•
각 ray 위에 있는 점들의 color 와 volume density 의 weighted sum 을 통해서 렌더링된 이미지 위의 pixel 색상을 결정하는 방법론
•
특정 점의 expected color c(r(t),d){\rm c}({\rm r}(t), {\rm d}) 는 특정 view direction 과 ray position 이 주어졌을 때 네트워크를 통해 예측이 되고, 이렇게 예측해낸 color 를 integration 하는 컨셉임.
•
다만, color 를 integration 할 때는 각 point 의 volume density σ(r(t))\sigma({\rm r}(t)) 와 occlusion 을 결정하는 요소인 T(t)T(t) 가 weight 로 들어감.
◦
T(t)T(t) 는 camera ray 를 따라서 본인의 앞에 있는 것들이 얼마나 방해하는지를 나타내는 요소임. 투과도로 볼 수 있음.
T(t)=exp⁡(−∫tntσ(r(s))ds)T(t)=\exp(-\int_{t_n}^{t}\sigma({\rm r}(s))ds)
•
하지만, continuous 하게 이를 적분할 수 없기 때문에 sampling 을 사용함.
C(r)^=∑i=1NTi(1−exp⁡(−σiδi))ciTi=exp⁡(−∑j=1i−1σjδj)\hat{C({\rm r})} = \sum_{i=1}^N T_i(1-\exp(-\sigma_i\delta_i)){\rm c}_i \quad T_i=\exp(-\sum_{j=1}^{i-1}\sigma_j\delta_j)
◦
Density 항목이 (1−exp⁡(−σiδi))(1-\exp(-\sigma_i\delta_i)) 인 이유는 line segment 항목인 δi\delta_i 가 크면 그 영향도 크게 하고 싶었기 때문임.

Training NeRF

•
각각의 ray 에 대해서 pixel 에 ray 를 rendering 하고, pixel reconstruction error 를 최소화하는 방향으로 학습을 진행함.
•
100+ 넘는 view 에서 3D 를 잘 만들어야 결과적으로 reprojection error 가 최소화 될 것이라는 인사이트에서 시작된 것임.

Hierarchical Volume Sampling

•
Ray 상에서 uniform interval 로 sampling 을 할 수도 있지만, 그렇게 하면 항상 보는 점들만 보게 됨.
•
여기서는 coarse pass 로 uniform interval 로 잘라둔 다음에 그 내부에서 uniform 하게 sampling 을 하는 방법을 고려할 수 있음.
•
Fine pass 로 sampling 할 때 volume density + transparency 기반으로 probability 를 주어 sampling 을 할 수 있음.
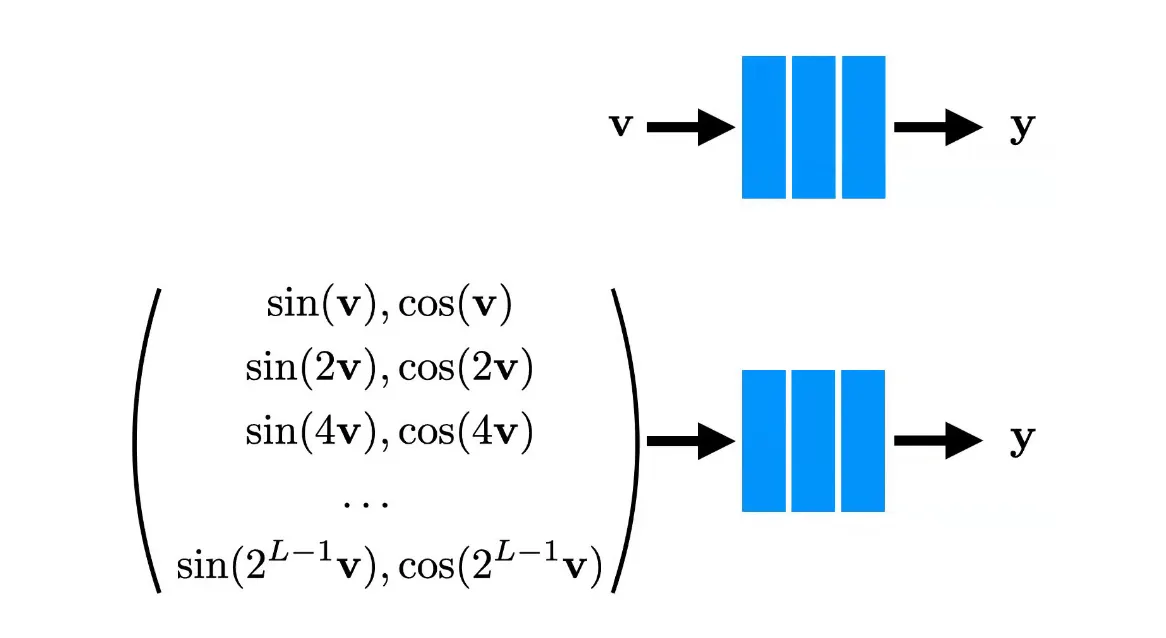
C≈∑i=1NTiαiciC \approx \sum_{i=1}^N T_i\alpha_i c_i

Positional Encoding

•
(x,y,z)(x,y,z) 가 조금 바뀌면 비슷한 색이 나올 것만 같은 format 임 → High resolution 을 rendering 을 만들어내기에 적합하지 않음!
•
Toy Example 로 다음과 같이 2D image 를 mapping 하여 memorize 하는 경우를 해봐도 이는 드러남.
•
Input 단에서 high dimensional function 으로 mapping 을 시켜버림.
•
이 positional encoding 이 major contribution 이며, transformer 가 이런 encoding 을 position 식별을 위해 사용했다면, 여기서는 high dimension mapping 을 위해 사용함.

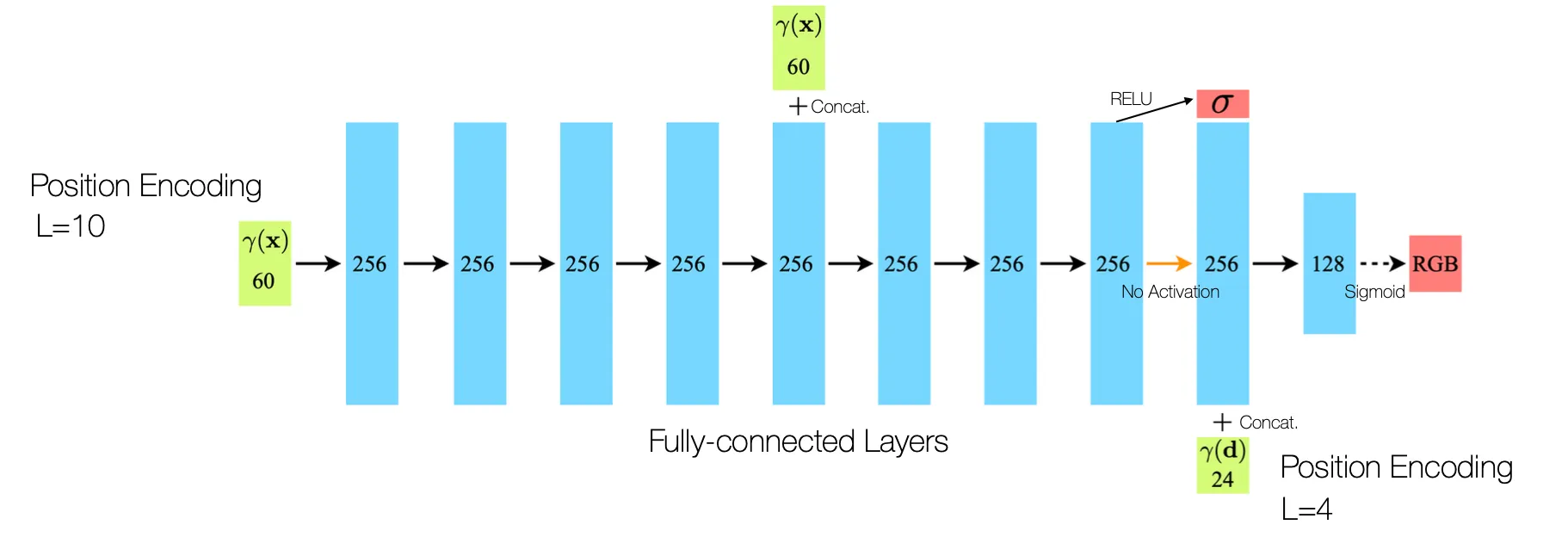
Network Architecture

•
Density 는 direction 과 무관한 요소라서 먼저 출력하고, direction 정보를 넣어서 color 를 뽑아냄.

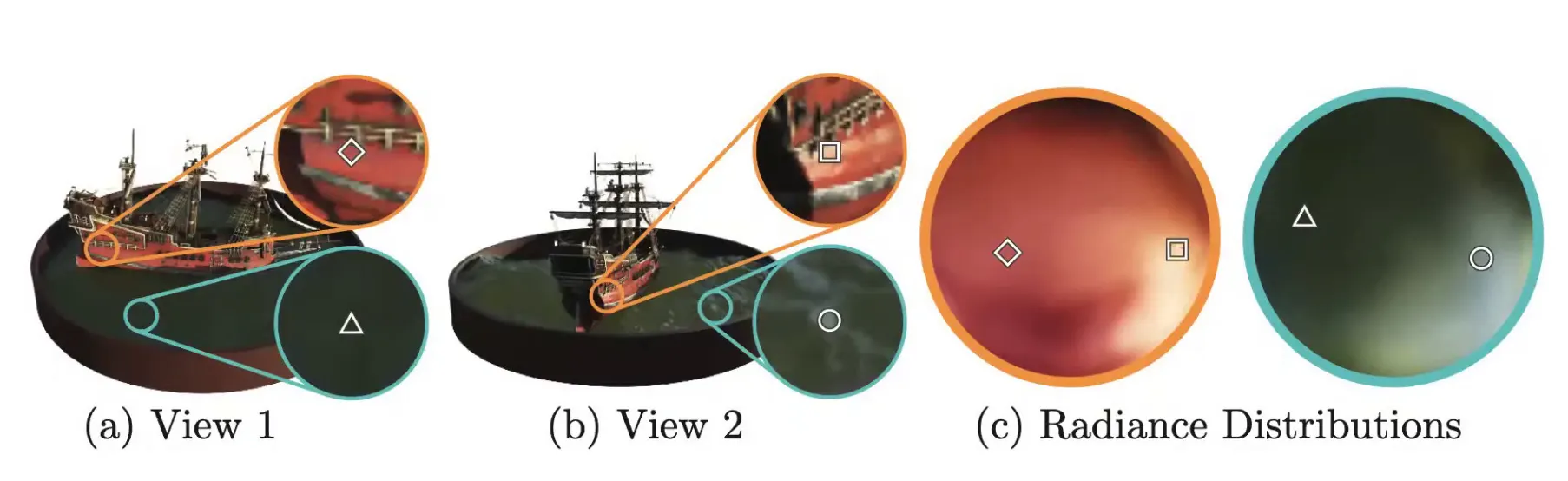
Dependency on View Direction

•
View-dependent 효과를 잘 표현해줌. (Non-Lambertian Materials)
◦
이것은 corresponding 에 기반한 방법론이 아니기 때문임.

Limitations

•
100+ 의 multiview image 가 필요함.
◦
RegNeRF 가 이를 타겟팅함.
•
Calibration parameters 도 같이 필요함.
◦
NeRF-W, Self-Calibrating NeRF (SCNeRF), BANMo 가 이를 타겟팅함.
•
Long rendering time
◦
FastNeRF 가 이를 타겟팅함.
•
Mutiview 가 동일한 lighting condition 에서 찍혀야 함. (short interval)
◦
NeRF-W, BANMo 가 이를 타겟팅함.
•
Static object only
◦
D-NeRF, Nerfies, BANMo 가 이를 타겟팅함.

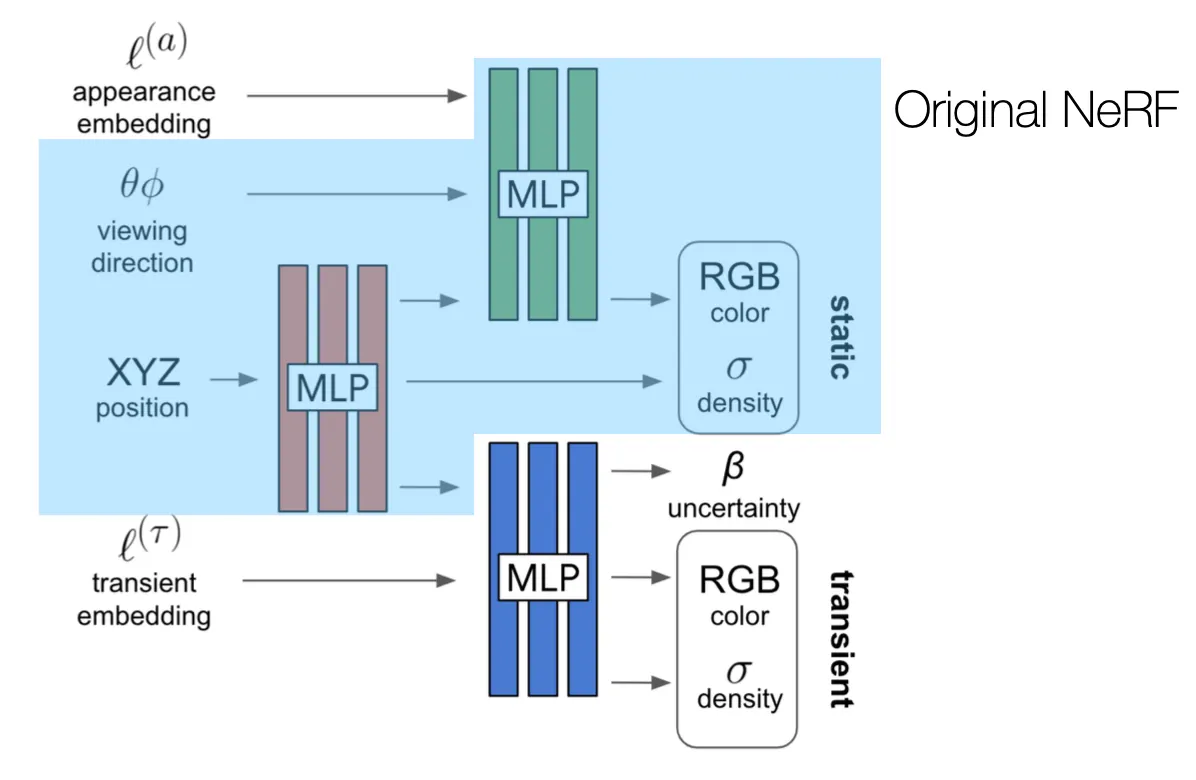
NeRF-W

•
Learnable appearance embedding 을 추가하여 lighting 으로 인한 효과를 표현할 수 있는 표현력을 추가함.
•
위 방법으로도 표현할 수 없는 이미지의 경우에는 weight 를 떨어뜨려서 해당 이미지의 영향을 줄여버리고 + uncertainty 라는 변수를 도입하여 해당 변수가 크면 영향을 줄여버림.

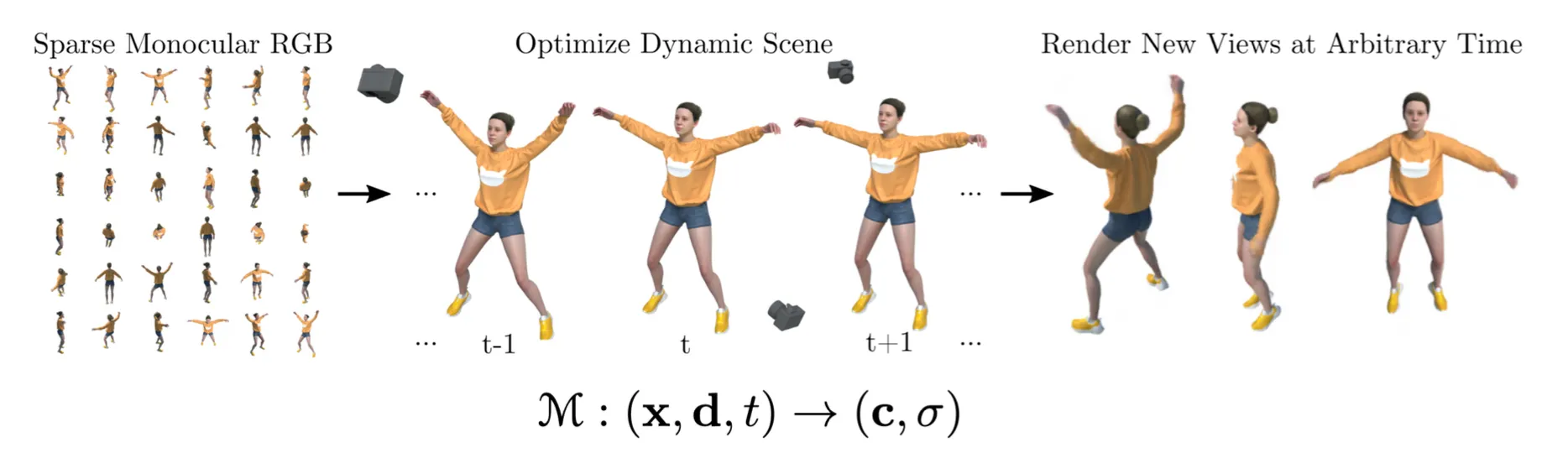
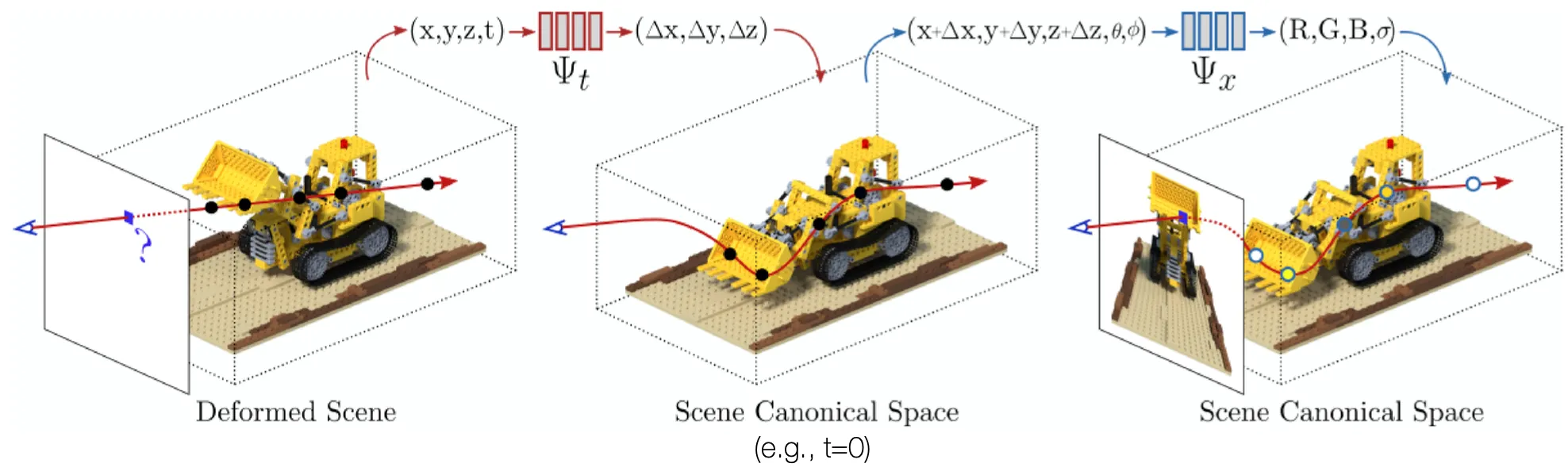
D-NeRF: Neural Radiance Fields for Dynamic Scenes

•
기존 NeRF 에 time 이라는 요소도 추가한 네트워크
•
먼저 시간까지 입력으로 넣어 Canonical Space 로의 mapping 에 필요한 변화를 뽑아낸 뒤에, 기존 NeRF 파이프라인을 활용함.

BANMo: Tackling The Most Challenging Scenario

•
Unknown Dynamic Objects
•
Casual Videos
•
Multiple Videos
•
Uncalibrated Cameras
•
Outputting color, density, neural skinning