본 세션에서는, 이전 세션에서 언급했던 Auto Encoder (AE), VAE (Variational Auto Encoder), 그리고 DAE (Denoising Auto Encoder) 와 유사한 형태의 네트워크인 Sparse Auto Encoder (SAE)에 대해서 알아보려고 합니다.
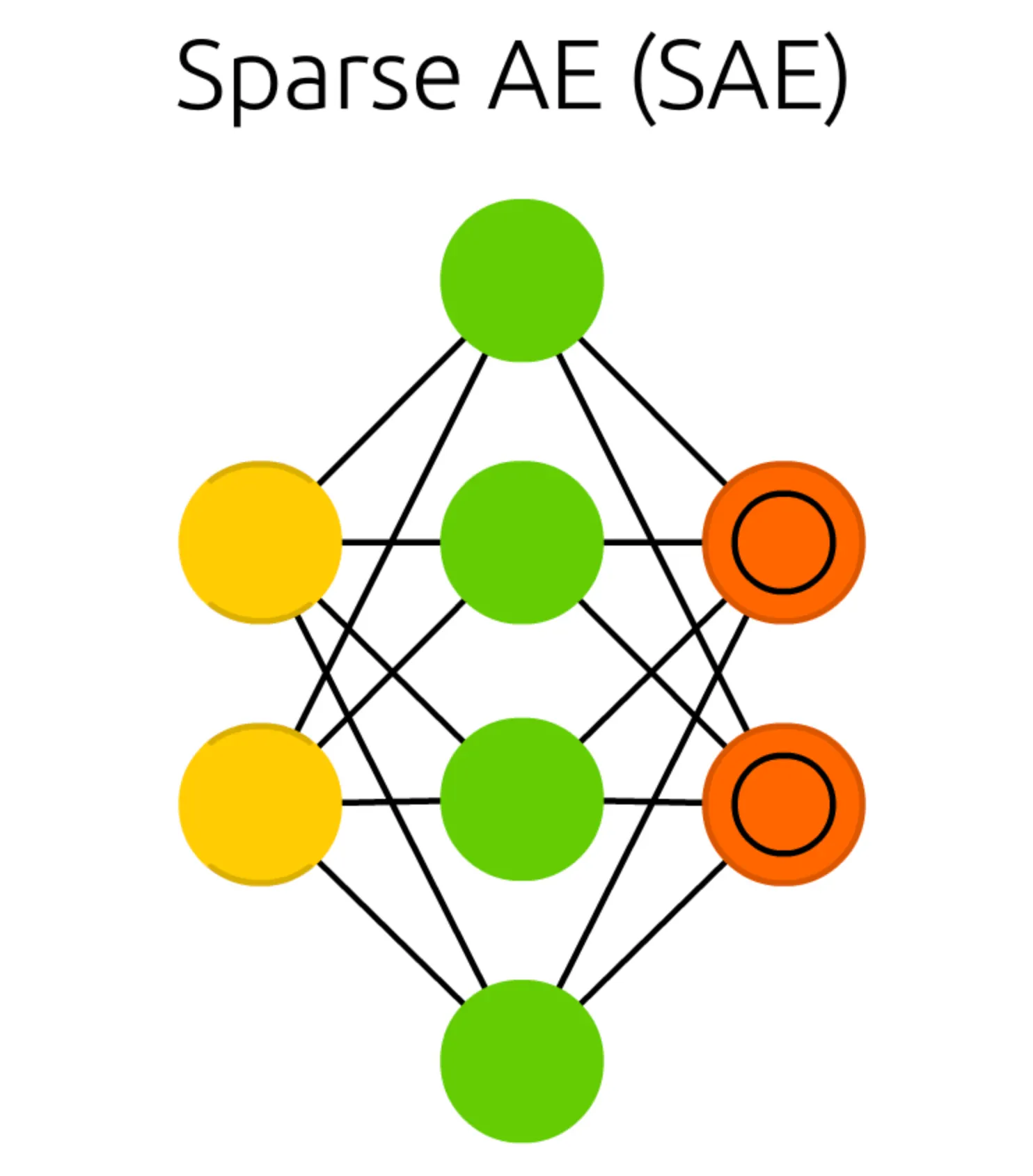
앞서 소개드렸던 Auto Encoder (AE) 와 비교하여 가장 먼저 보이는 구조의 특징적인 변화는 Hidden Cell 의 dimension 이 Input Cell 및 Match Input Output Cell 의 dimension 보다 크다는 점입니다. 기존의 Auto Encoder 구조에서는 SAE (Sparse Auto Encoder) 와 같은 형태가 constraint 로 인해 존재할 수 없었습니다.
그렇다면, Sparse Auto Encoder (SAE) 는 AE (Auto Encoder) 의 이름을 갖고 있으면서도 어떻게 Hidden Cell 의 dimension 이 Input Cell 및 Match Input Output Cell 보다 클 수 있는 것일까요?
그것은 AE (Auto Encoder) 가 구조로써 제약하고 있는 요소를 SAE (Sparse Auto Encoder) 는 연산으로 제약하고 있기 때문입니다. 실제로, 둘은 결과적으로는 같은 것을 제약하고 있고, 동일한 기능을 수행할 수 있습니다.
여기까지 들으시면 읭? 이건 또 무슨 소리야! 하실 분들이 많으실 것 같습니다.
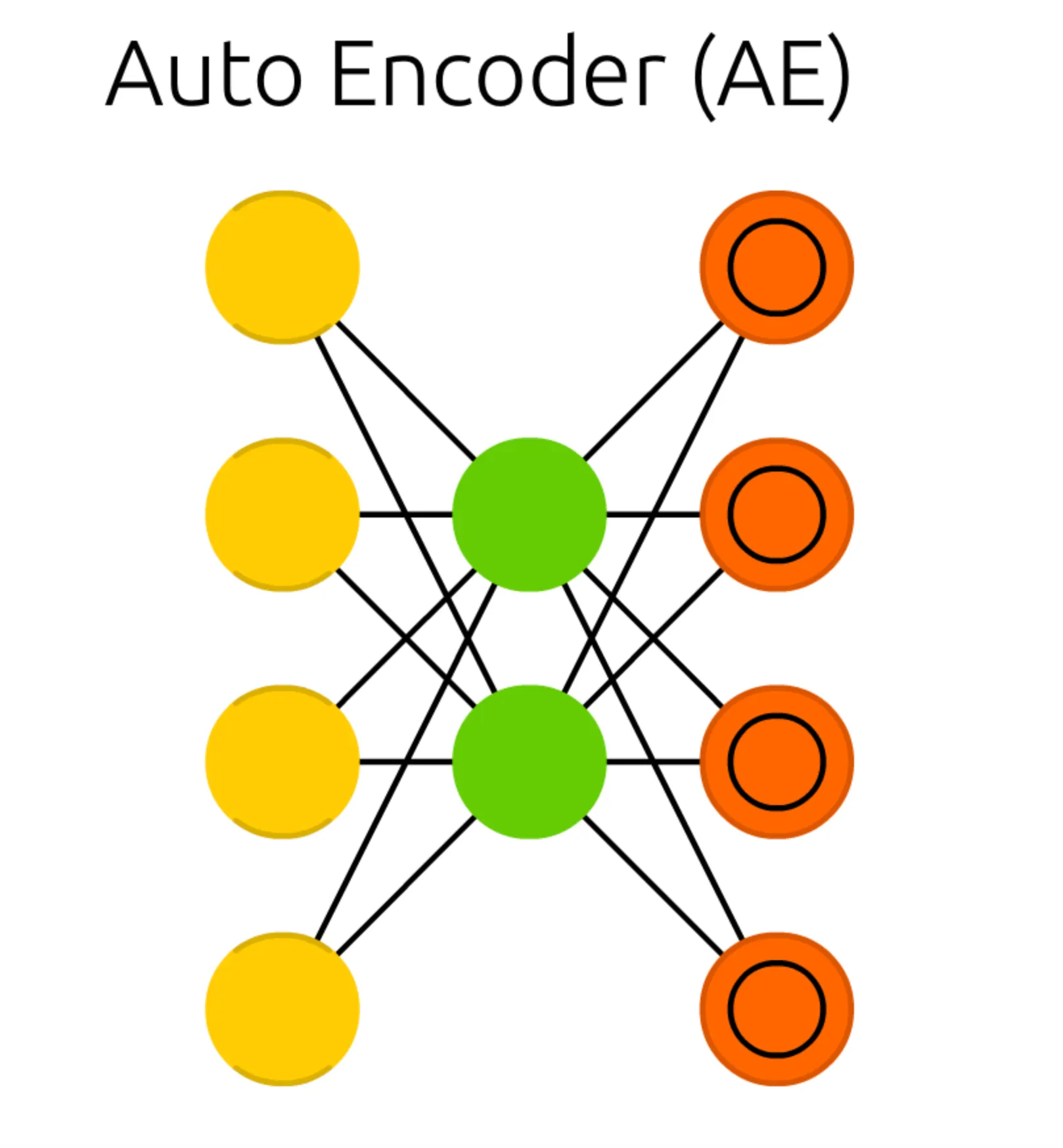
다시 AE (Auto Encoder) 의 구조를 빌려보겠습니다.
AE (Auto Encoder) 구조가 가지고 있는 두 가지 제약조건은 다음과 같았습니다.
1.
Input Cell 과 Output Cell 의 dimension 이 같아야 합니다.
2.
Hidden Cell 의 dimension 은 Input Cell 및 Output Cell (AE 에서는 Match Input Output Cell 이라고 부르기도 합니다.) 작아야 합니다.
여기서 SAE (Sparse Auto Encoder) 와 다른 AE (Auto Encoder) 의 제약조건은 2번입니다. 그리고 이 제약조건은 AE (Auto Encoder) 의 feature extraction 이라는 목적성에 기반한 필연적인 구조였습니다.
여기까지 설명드리면, 눈치가 빠르신 분들은
SAE (Sparse Auto Encoder) 는 굳이 Hidden Cell dimension 을 제약하지 않아도, feature extraction 을 구현할 수 있구나!!
라는 것을 알아차리셨을 것 같습니다.
맞습니다.
SAE (Sparse Auto Encoder) 는 구조를 통해 feature extraction 을 강제하지 않고, 특별한 loss function 을 통해 feature extraction 을 구현합니다.
특별한 loss function 이라는 명칭을 붙이기는 했지만, 어려운 내용은 아닙니다. AE (Auto Encoder) 에서 원하는 extracted 된 latent vector 는 결과적으로 네트워크를 통해 나오는 activation 값이고, loss function 에서 activation 이 큰 결과에 대해 penalize 를 해줄 수 있는 항목을 추가하면 됩니다.
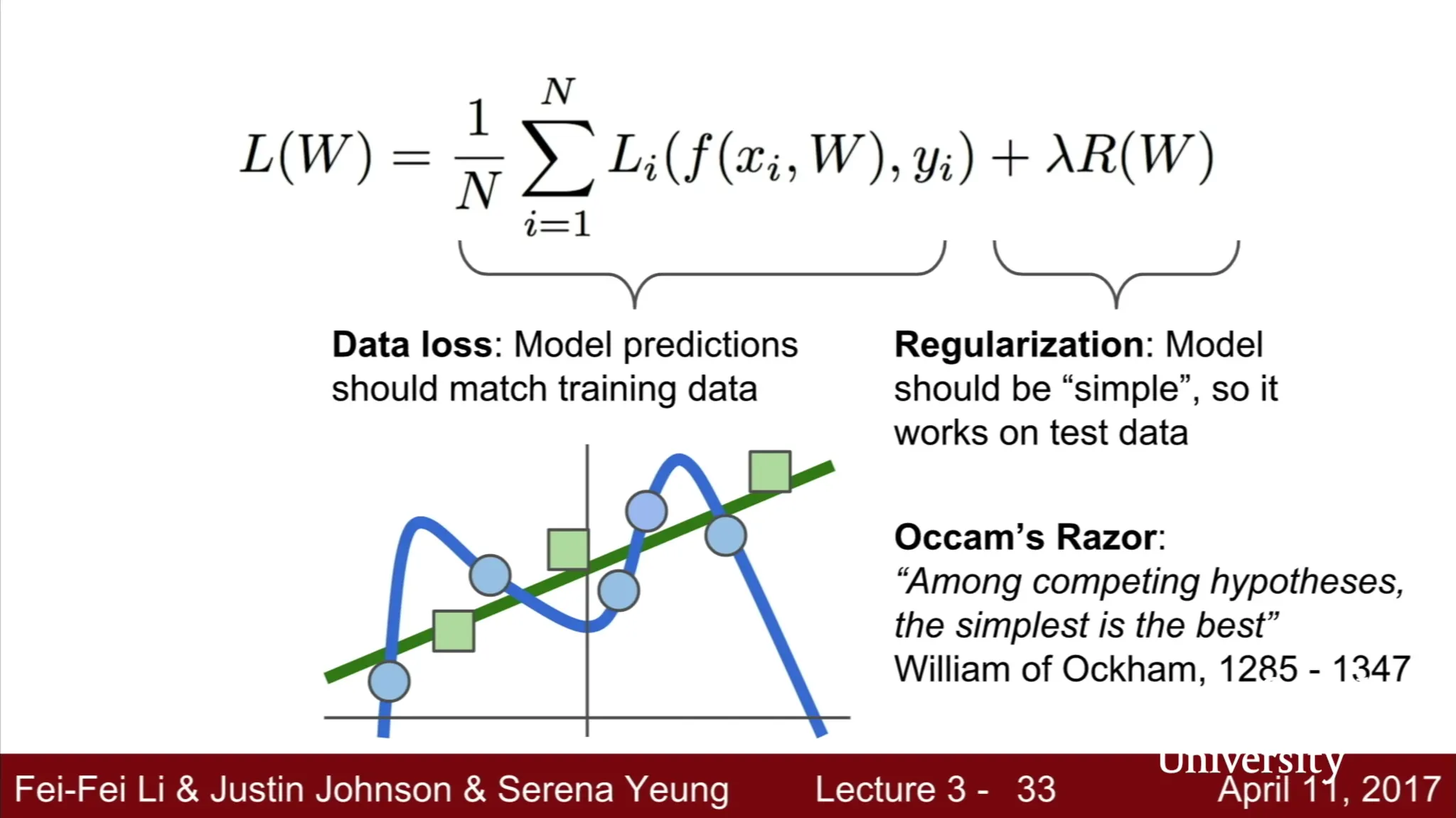
특정 항목이 큰 것에 대해 penalize 를 하는 것으로 가장 기본적인 방법이 regularization 입니다. 이는 기본적으로는 weight 에 대해 적용하여 수많은 유효 weight 가 결과에 영향을 미쳐 overfitting 이 되는 것을 억제하기 위해 사용됩니다.
위 예시는 cs231n 제 3강에서 발췌한 사진입니다. 슬라이드만으로 다소 이해하기 어려울 수도 있는데, 간단하게 첨언하자면 regularization 이 없어 n 차원 근사에서 최고 차원이 0 보다 유의미하게 커서 고차원 근사가 될 경우와, regularization 이 적용되어 높은 차원이 적절하게 0 과 유사하여 저차원 근사가 될 경우를 비교한 것으로 보시면 됩니다. 일반적으로, training data 뿐만이 아니라 test data 에도 모델의 성능이 좋아야 하기 때문에 모델의 generalization 을 추가하는 역할을 해주는 방법론이라고 보시면 됩니다.
Regularization 에 대한 설명이 길었는데, SAE (Sparse Auto Encoder) 에서는 overfitting 을 방지하기 위함이 아니라 모델을 통해 산출될 latent vector 의 유의미한 dimension 을 줄일 수 있는 수단으로 regularization 을 사용합니다. 앞서 설명드린 regularization 과의 차별점이 있다면 앞선 설명에서는 weight regularization 을 예시로 들었는데 이번 경우에는 activation regularization 입니다. Regularization 할 항목이 weight 이냐, activation 이냐가 다른 점입니다.
기존의 AE (Auto Encoder) 의 loss function 은 아래와 같았습니다.
간단하게, 각 픽셀 값의 차이를 이용해 정의한 loss function 입니다. 물론, VAE (Variational Auto Encoder) 에서 소개드린 Cross Entropy Loss 를 사용해도 무방합니다. 둘 모두 원본과 생성본의 차이를 최소화하는 방향으로 설계되었기 때문입니다.
Sparse Auto Encoder (SAE) 는 위 loss function 에서 regularization term 을 추가합니다.
위 식의 경우는 L1 regularization 을 추가한 loss function 입니다. regularize 하고 싶은 activation (SAE 의 경우에는 latent vector 로 사용할 activation) 각각의 절댓값의 summation 형태를 작게 만들 수 밖에 없는 형태의 loss function 을 설계하는 것입니다. 때문에 0 에 굉장히 가까운 activation 이 많고, 해당 activation 은 유의미하지 못하다- 고 판단하여 실제로 유의미한 latent vector 의 dimension 은 작다고 보는 것입니다.
L1 regularization 말고도 다른 regularization 을 사용할 수도 있습니다. 기준값과의 Kullback-Leibler Divergence 를 사용하는 것입니다.
이전 VAE (Variational Auto Encoder) 에서도 잠깐 설명드렸었는데 Kullback-Leibler Divergence 는 두 값이 비슷할 수록 작습니다. 즉, 해당 term 도 loss function 의 최소화라는 목표 아래에서 activation 을 기준값과 비슷하게 만들어 줄 수 있다는 것입니다. 저희가 해야할 것은 기준값을 0 과 유사하게 설정하는 것 뿐입니다.
이제 SAE (Sparse Auto Encoder) 에서 loss function 을 통해 AE (Auto Encoder) 가 설정했던 제약조건을 구현했다는 말이 이해가 되셨을 것이라 믿습니다. 
이렇게 이번 세션에서는 Sparse Auto Encoder (SAE) 에 대해서 알아보는 시간을 가졌습니다. Sparse Auto Encoder (VAE) 의 목적은 AE (Auto Encoder) 와 같지만, AE (Auto Encoder) 가 목적 달성을 위해 필연적으로 가져야 했던 구조의 제약조건을 SAE (Sparse Auto Encoder) 에서는 loss function 의 재설계로 옮겼다는 사실을 주요하게 알아두시면 좋을 것 같습니다.