Duplicate

Lecture 2 ~ 3 | MDPs and RL

Tags
Date

Markov Decision Processes

•
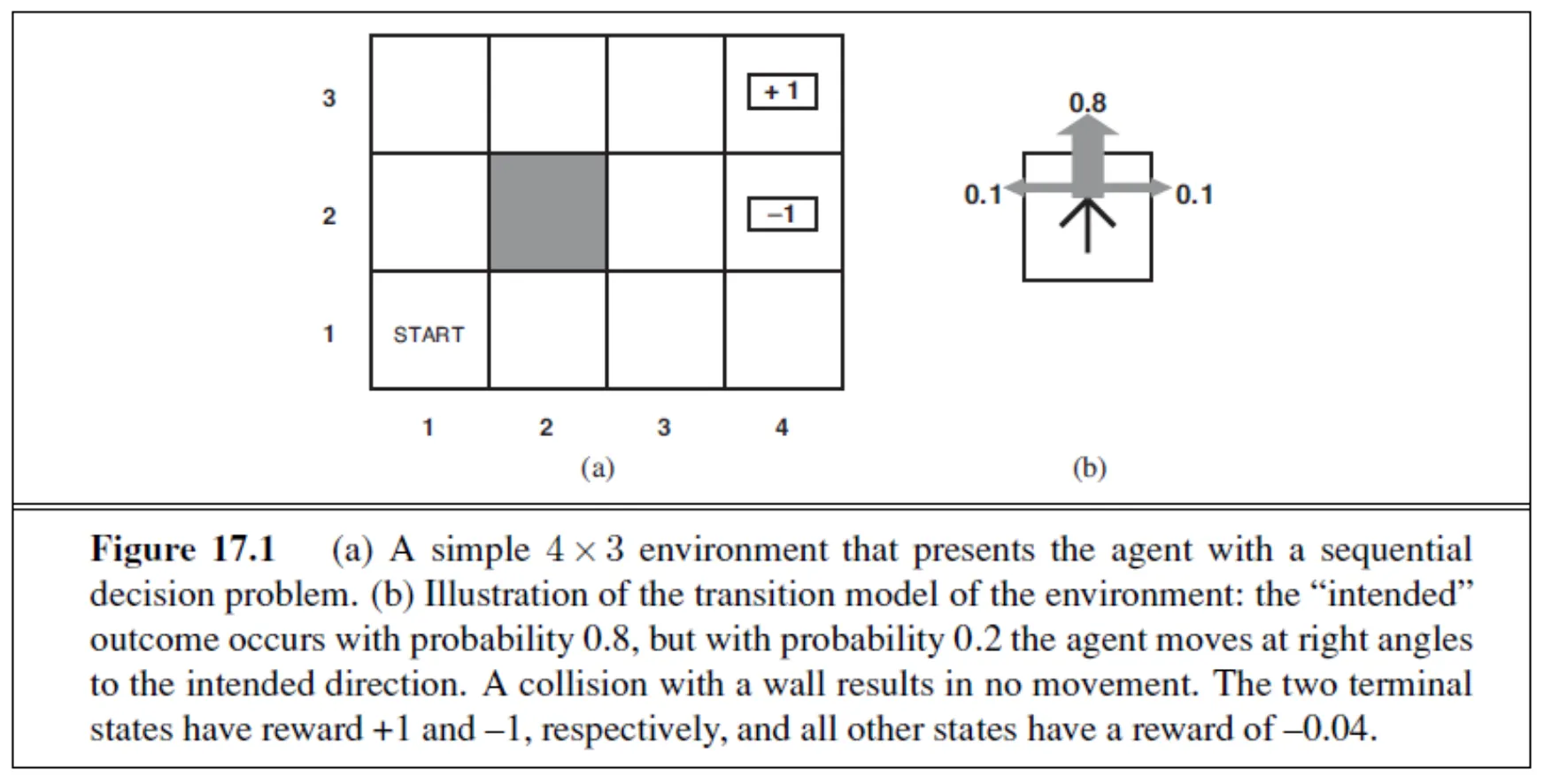
Fully observable, Stochastic 한 환경 (Non-deterministic, 확률에 기반)
•
additive reward functions
•
sequential decision problem
•
다음과 같이 구성
◦
Set of states S\mathcal S
◦
Set of actions Actions(s) in each state s∈Ss \in \mathcal S
◦
Transition model P(s′∣s,a)P(s'|s,a)
◦
Reward function R(s)R(s)
•
Policy 는 현재 state 에서 어떤 action 을 택해야 하는지에 대한 함수
•
Optimal Policy 는 highest expected utility 를 가지는 policy

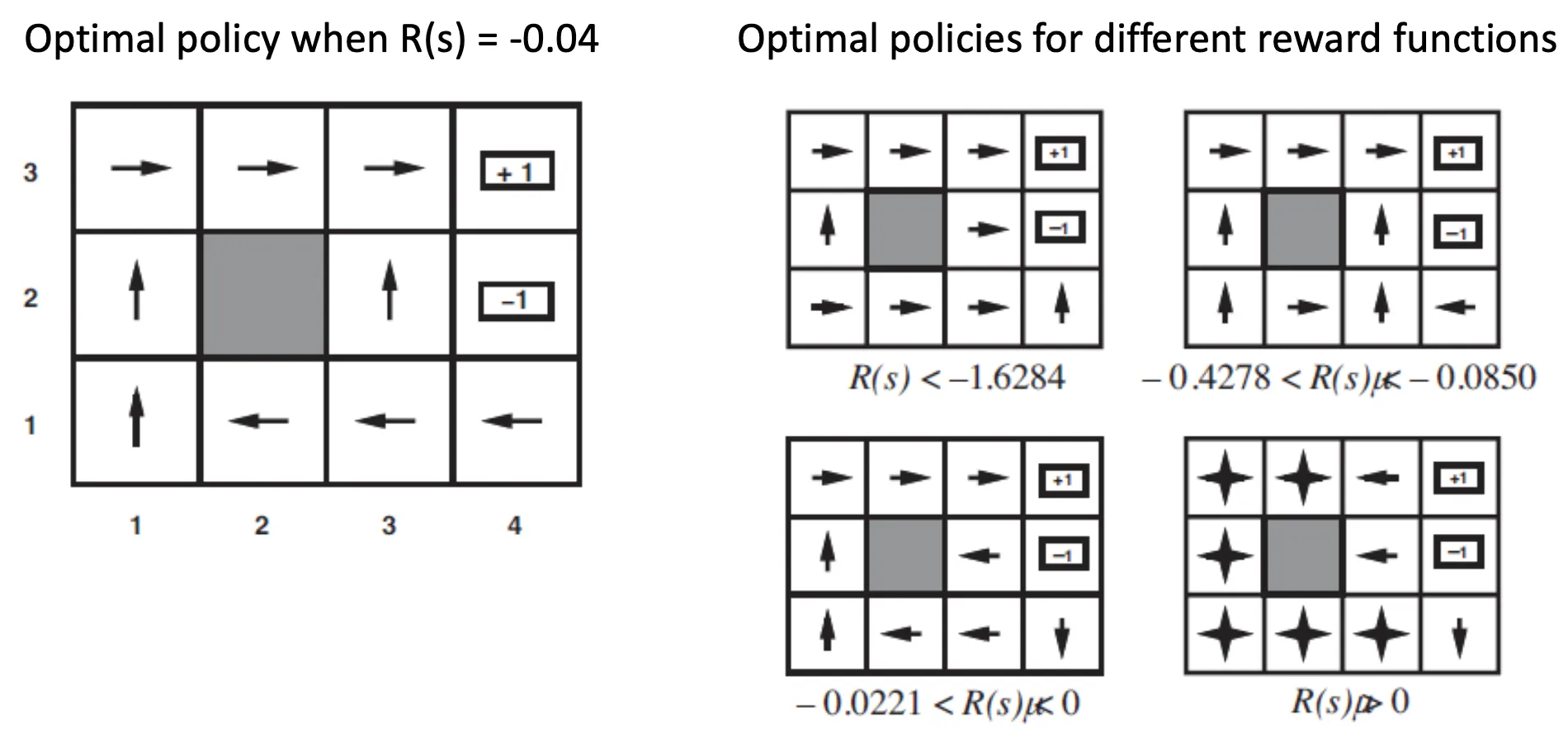
Example of Markov Decision Processes

•
각 장소에 부여된 Reward Function 에 따라서 optimal policy 가 달라짐

Utilities Over Time

•
Finite Horizon Problem: 결정 문제가 time NN 에서 끝남
◦
남은 시간도 condition 개념이라서, 특정 state 에 대한 optimal action 이 time 에 따라 달라짐
•
Infinite Horizon Problem: 결정 문제에 time limit 이 없음
◦
특정 state 에 대한 optimal action 이 time 에 따라 달라지지 않음
◦
Optimal policy 는 시간에 따라서 변하지 않음

Rewards Under Stationarity

•
Additive Rewards
◦
각 state 에서 얻은 reward 의 합이 최종 reward
•
Discounted Rewards
◦
γ\gamma factor 가 지속적으로 곱해진 채로 각 state 에서 얻은 reward 를 합해 최종 reward 결정
◦
∣R(s)∣≤Rmax|R(s)| \le R_{max} 로 가정하면, 최종 reward 는 bounded 되어 있음.
U([s0,s1,s2,… ])=∑t=0∞γtR(st)≤∑t=0∞γtRmax=Rmax1−γU([s_0,s_1,s_2, \dots]) = \sum_{t=0}^{\infty}\gamma^t R(s_t) \le \sum_{t=0}^{\infty}\gamma^t R_{max} = \frac{R_{max}}{1-\gamma}

Optimal Policy and Utilities

•
Expected Utility by executing π\pi starting from ss
Uπ(s)=E[∑t=0∞γtR(St)]U^{\pi}(s) = \mathbb E[\sum_{t=0}^{\infty}\gamma^t R(S_t)]
◦
expected utility 를 최대로 만드는 π\pi 가 optimal policy → 이걸로 만드는 utiliy 가 True Utiliy of State Uπ∗(s)=U(s)U^{\pi^*}(s) = U(s)
◦
Infinite Horizon Problem 은 starting state 에 관계 없이 optimal policy 가 동일하다.
•
Principle of Maximum Expected Utility
π∗(s)−arg max⁡a∈A(s)∑s′P(s′∣s,a)U(s′)\pi^*(s) - \argmax_{a \in A(s)} \sum_{s'}P(s'|s,a)U(s')

Value Iteration

•
Bellman Equation
U(s)=R(s)+γmax⁡a∈A(s)∑s′P(s′∣s,a)U(s′)U(s) = R(s) + \gamma \max_{a \in A(s)} \sum_{s'} P(s' | s, a)U(s')
•
n 개의 state 가 있는 경우 n 개의 Bellman Equation 과 n 개의 variable 이 존재
•
Value Iteration 이 optimal solution 을 줄 수 있음

Convergence of Value Iteration

•
Contraction
◦
두 개의 값을 입력으로 받아서 두 개의 출력을 내는데, 출력의 차이가 입력의 차이보다 작아지는 함수
◦
e.g., 2로 나누는 함수
∥x2−y2∥≤∥x−y∥\| \frac{x}{2} - \frac{y}{2} \| \le \| x - y\|
◦
fixed point: function 을 거쳐도 자기 자신인 값 (2로 나누는 함수에 대해서는 0)
•
BB 를 Bellman Update 라고 하고, 이를 utility function 에 적용하다보면, fixed point 인 optimal solution 에 수렴하게 되어 있음. → 복습
•
Discount factor 가 크면 먼 미래를 생각할 필요가 없음.

Convergence Rate

•
Contraction
∥BUi−BUi′∥≤γ∥Ui−Ui′∥\| BU_i - BU_i'\| \le \gamma \|U_i -U_i'\|
•
True Utility 에 대해서 U=BUU=BU, ∥BUi−U∥≤γ∥Ui−U∥\|BU_i - U\| \le \gamma \|U_i-U\|
◦
때문에 value iteration 은 true utility 로 exponential 하게 converge 함.
•
error bound ϵ\epsilon 미만을 가지기 위해 필요한 iteration 수를 계산할 수 있음. → 복습
◦
Termination Condition
∥Ui+1−Ui∥<ϵ(1−γ)/γ→∥Ui+1−U∥<ϵ\|U_{i+1} - U_i \| < \epsilon (1-\gamma) / \gamma \to \|U_{i+1} - U\| < \epsilon
•
Policy Loss: ∥Uπi−U∥\|U^{\pi_i} - U\|

Policy Iteration

•
Utility Esimate 가 부정확하더라도 optimal policy 를 얻을 수 있음
•
다음 두 단계로 이루어짐
◦
Policy Evaluation
◦
Policy Improvement

POMDP (Partially Observable Markov Decision Process)

•
MDP 와 같지만 state 가 observable 하지 않음
•
Belief State b(s)b(s): 모든 state 에 대한 probability distribution
•
observation 에 기반하여 filtering 을 사용하여 bb 를 업데이트할 수 있음
◦
kalman filter 가 한 예시임
b′(s′)=αP(e∣s′)∑sP(s′∣s,a)b(s)b'(s') = \alpha P(e|s')\sum_s P(s'|s, a)b(s)
•
POMDP 에서 optimal action 은 현재 belief state 에만 기반함
•
Optimal Policy 는 실제 agent 의 state 에 기반하는 것이 아니라 belief state 에 기반함 (agent 의 state 는 관측 불가능하기 때문)
•
state 수가 무한하기 때문에 value iteration 을 적용할 수 없음

From POMDP to MDP

•
Belief-state space 에서 동작하는 transition model
P(b′∣b,a)=P(b′∣a,b)=∑eP(b′∣e,a,b)P(e∣a,b)==∑eP(b′∣e,a,b)∑s′P(e∣s′)∑sP(s′∣s,a)b(s)P(b'|b,a) = P(b'|a, b) = \sum_e P(b'|e,a,b)P(e|a,b)= \\ = \sum_e P(b'|e,a,b) \sum_s' P(e|s') \sum_s P (s'|s,a)b(s)
•
Reward function for belief states
σ(b)=∑sb(s)R(s)\sigma(b) = \sum_s b(s) R(s)
◦
reward 에 대한 expectation 느낌

Two Observations

•
physical state ss 에서 시작하여 고정된 conditional plan pp 을 실행 시 utility: αp(s)\alpha_p(s)
•
U(b)U(b) 는 piecewise linear 하고 convex 함 → 두 개의 observation 에 의해 (detail 안 다룸)
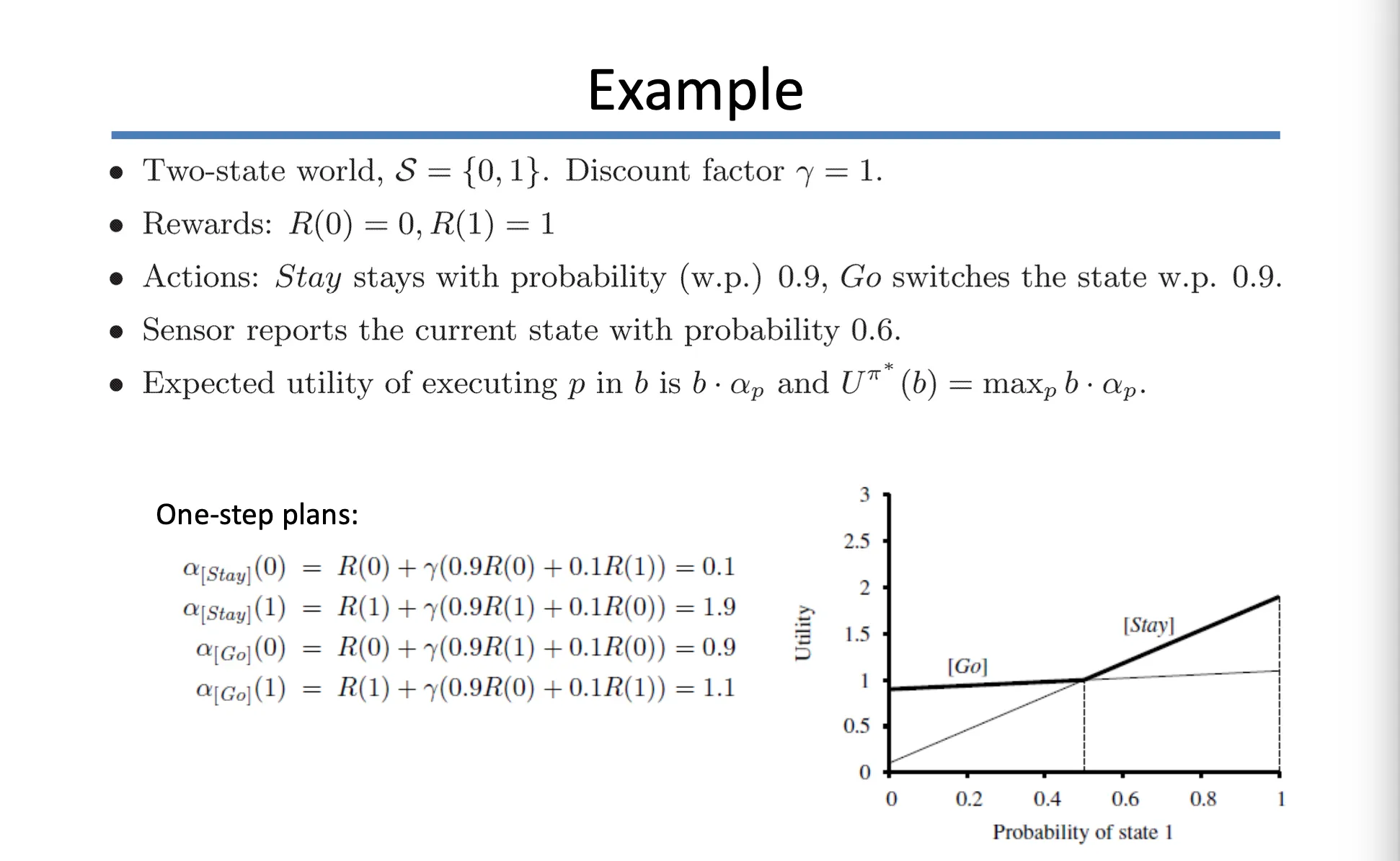
Example
•
위 예시처럼, αp(s)\alpha_p(s) 를 각각 구할 수 있음
•
probability of state 1 을 vary 함에 따라서 utility 그래프를 그릴 수 있음

Reinforcement Learning

•
MDP 는 complete model 이 알려져 있음 → optimization problem
•
Reinforcement Learning 은 MDP 와 비슷하지만, complete model 이 알려져 있지 않음
◦
Transition Model, Reward 등이 알려지지 않음
◦
관측된 reward (data 를 얻어서) 로 환경에 대한 optimal policy 를 배움
•
세 가지 agent 의 종류
◦
Behavior Cloning: state 에서 action 을 직접적으로 연결하는 policy 를 배움
◦
Utility-based: agent 가 state 에 따른 utility function 을 학습하여 expected outcome 을 최대화하는 action 을 선택함
◦
Q-Learning: → 복습
Passive Reinforcement Learning
Direct Utility Estimation
•
Utility of a state (value of a state or reward-to-go)
•
Utility function 을 예측하기 위해 supervised learning 을 활용할 수도 있음.
Adaptive Dynamic Programming (ADP)
•
Sample 로부터 transition model 을 배움 (ML estimation)
•

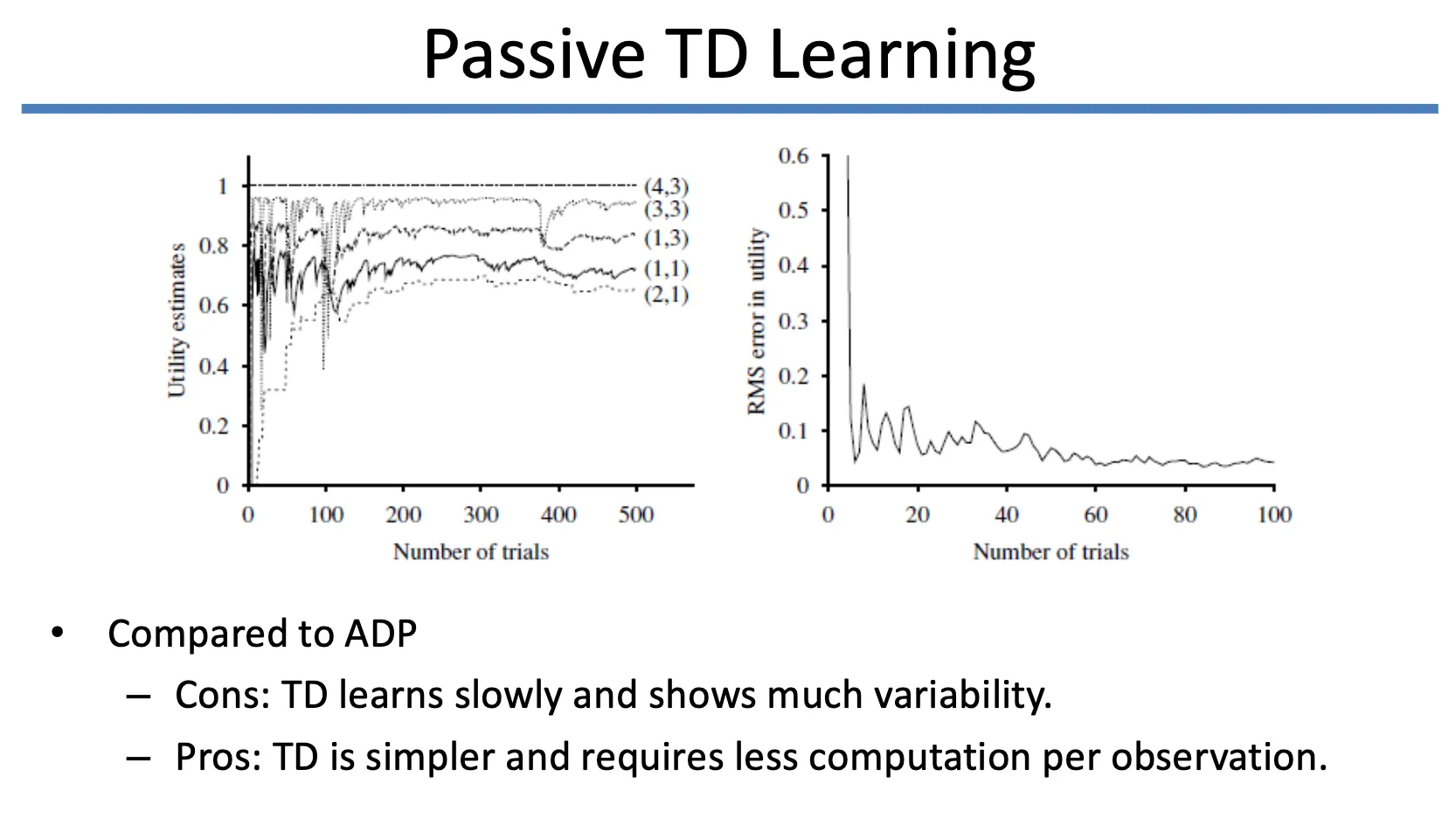
Temporal Difference (TD) Learning

Uπ(s)←Uπ(s)+α(R(s)+γUπ(s′)−Uπ(s))U^{\pi}(s) \larr U^{\pi}(s) + \alpha (R(s) + \gamma U^{\pi}(s') - U^{\pi}(s))
•
Current Estimate 와 One-Step Further Estimate 을 보고
◦
비슷하면, 유지함
◦
one-step 이 크면 현재를 underestimate 하고 있으니 현재 estimate 을 높임
◦
one-step 이 작으면 현재를 overderestimate 하고 있으니 현재 estimate 을 낮춤
•
Gradient descent 와 유사하게 현재의 estimate 을 optimize 함
Active Reinforcement Learning
•
Exploration Function
Action-Utility Function
•
Q function: state ss 에서 action aa 를 할 확률
U(s)=max⁡sQ(s,a)U(s)=\max_s Q(s,a)
•
Q-Learning 은 model-free 한 방법론임
◦
P(s′∣s,a)P(s'|s,a) 와 같은, action selection 을 위한 transition model 이 필요없음
Q-Learning
Q(s,a)←Q(s,a)+α(R(s)+γmax⁡a′Q(s′,a′)−Q(s,a))Q(s,a) \larr Q(s,a) + \alpha (R(s) + \gamma \max_{a'}Q(s', a')- Q(s,a))
SARSA
•
State-Action-Reward-State-Action
•
Update Rule
Q(s,a)←Q(s,a)+α(R(s)+γQ(s′,a′)−Q(s,a))Q(s,a) \larr Q(s,a) + \alpha (R(s) + \gamma Q(s', a') - Q(s,a))
◦
maximize function 이 제거된 형태임
◦
greedy agent 에 대해서, SARSA 는 Q-Learning 과 동일함
◦
explorative agent 에 대해서, 다름을 보임
▪
Q-Learning (off-policy), SARSA (on-policy)

Function Approximation

•
Utility function 이나 Q-function 을 유한한 개수의 basis function 으로 근사함.
U^θ(s)=θ1f1(s)+θ2f2(s)+⋯+θnfn(s)\hat{U}_\theta(s) = \theta_1f_1(s) + \theta_2f_2(s) + \dots+ \theta_nf_n(s)
•
Policy Search
•
Gradient descent 로 policy 를 직접적으로 찾는 방법
•
policy function 을 parameterize (아래 식이 argmax 아니어야 하냐고 언급하심)
π(s)=max⁡aQ^θ(s,a)\pi(s) = \max_a \hat{Q}_\theta (s,a)
•
Policy improvement
◦
Reinforce