Duplicate

Lecture 10 | Projective Homography

형태
Computer Vision
수강 일자
2022/10/05

Overview: Camera Projection

•
3D object 에 반사된 광원의 빛이 카메라로 들어가 이미지의 픽셀로 맺히게 됨.
•
3D 공간을 2D 공간으로 변형하면서 신기한 특성들이 보이게 됨.
◦
평형인 선들이 더 이상 평행이 아니고 한 점으로 모임. (Vanishing Point)
◦
정사각형이던 건물의 벽이 정사각형으로 보이지 않음.

Euclidean Geometry

•
Euclidean 의 의미
◦
두 점 간의 최소 거리는 두 점을 이은 직선의 거리
◦
어떠한 삼각형이던 내부 각의 합은 180°180\degree
◦
수직인 두 직선의 각은 90°90\degree
◦
평행인 두 직선은 절대 만나지 않음

What is Projective Geometry? PN{\mathbb{P}}^N

•
평행인 직선은 한 점에서 만나게 됨 (Vanishing Point)
•
원은 타원으로 보일 수 있음
•
직사각형은 평행사변형으로 보일 수 있음
•
각도, 거리, 거리의 비율은 유지되지 않음

Representing A 2D Point in 2D Euclidean Space

•
(x1,x2)T(x_1,x_2)^T 형태로 2차원 점을 나타낼 수 있음

Representing A 2D Point in R2\mathbb{R}^2

•
(x1,x2,1)T(x_1,x_2,1)^T 형태로 3차원의 선을 나타낼 수 있음. (z=1z=1 과 만나는 점을 통해 선을 표현)
•
Projective Space P2\mathbb{P}^2
◦
[x1x21]=[kx1kx2k]\begin{bmatrix} x_1 \\ x_2 \\ 1 \end{bmatrix} = \begin{bmatrix} kx_1 \\ kx_2 \\ k \end{bmatrix}→ z=1z=1 에 projection 했을 때의 위치가 동일하기 때문.
◦
(0,0,0)(0,0,0) 은 정의 되어있지 않음 → P2=R2−{(0,0,0)}\mathbb{P}^2 = \mathbb{R}^2-\{(0,0,0)\}
◦
[x1x20]\begin{bmatrix} x_1 \\ x_2 \\ 0 \end{bmatrix} 은 ∞\infty 에 있는 점을 의미함.

Projective Space P2{\mathbb P}^2

•
Homogenous coordinate 를 사용한 3-dim vectors 로 표현됨
•
(0,0,0)(0,0,0) 은 정의되지 않음 → P2=R3={(0,0,0)}{\mathbb P}^2 = {\mathbb R}^3 = \{(0,0,0)\}
•
Scale 만 다른 homogenous vecctor 는 equivalent 함
•
Projective space 에서 Euclidean 으로의 변환은 첫, 두 번째 항을 세 번째 항으로 나눠주면 됨
(x1,x2,x3)T→(x1/x2,x2/x3)(x_1,x_2,x_3)^T \rarr (x_1/x_2, x_2/x_3)
•
Inhomogenous coordinate 과는 다르게 무한대에 있는 점을 표현할 수 있음 (Ideal points 혹은 point at infinity 라고 함) → 굳이 여러 경우에서 finite, infinite (parallel, not parallel) 를 나눠가며 판단할 필요가 없음!!
[x1x20]\begin{bmatrix} x_1 \\ x_2 \\ 0 \end{bmatrix}

Representing 2D Lines in Homogenous Coordinates

•
x2=αx1+β→0=αx1+−x2+βx_2=\alpha x_1+\beta \rarr 0=\alpha x_1 + -x_2 + \beta
•
Line equation 에서 line 은 다음과 같이 표현됨
{(x1,x2)∣ax1+bx2+c=0}\{ (x_1,x_2)|ax_1+bx_2+c = 0 \}
[x1x21][abc]=0\begin{bmatrix} x_1 & x_2 & 1 \end{bmatrix} \begin{bmatrix} a \\ b \\ c \end{bmatrix} = 0
•
Homogenous coordinate 에서 line 은 l=(a,b,c)Tl=(a,b,c)^T 로 표현됨
•
Line ll 위에 있는 점들은 다음과 같이 표현됨
{x∣xTl=0}\{ x | x^Tl = 0\}

Degree of Freedom(DoF)

•
Independent variable 의 수
•
Homogenous coordinate 의 DoF 는 2

The Line Joining Two Points

•
Homogenous coordinate 에서 두 점 x\rm x, x′\rm x' 을 지나는 직선은 두 점의 외적임
l=x×x′l=\rm x \times x'
◦
l⋅x=lTx=0l\cdot {\rm x} = l^T {\rm x} = 0 → x\rm x 가 ll 위에 있다-
◦
l⋅x′=lTx′=0l\cdot {\rm x'} = l^T {\rm x'} = 0 → x′\rm x' 가 ll 위에 있다-
•
Cross product 의 계산
a×b=∣ijka1a2a3b1b2b3∣=∣a2a3b2b3∣i−∣a1a3b1b3∣j+∣a1a2b1b2∣k=(a2b3−a3b2a3b1−a1b3a1b2−a2b1)\begin{align*} \rm a\times b &= \begin{vmatrix} i & j & k \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} = \begin{vmatrix} a_2 & a_3 \\ b_2 & b_3 \end{vmatrix}i - \begin{vmatrix} a_1 & a_3 \\ b_1 & b_3 \end{vmatrix}j + \begin{vmatrix} a_1 & a_2 \\ b_1 & b_2 \end{vmatrix}k \\ &= \begin{pmatrix} a_2b_3-a_3b_2 \\ a_3b_1-a_1b_3 \\ a_1b_2-a_2b_1 \end{pmatrix} \end{align*}
•
Cross product 는 skew-symmetric matrix 로 표현 가능함
◦
Matrix multiplication 으로 표현하는 것의 이점들을 가져갈 수 있음!
a×b=[0−a3a2a30−a1−a2a10](b1b2b3)=(a2b3−a3b2a3b1−a1b3a1b2−a2b1)\rm a\times b = \begin{bmatrix} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{bmatrix} \begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} = \begin{pmatrix} a_2b_3-a_3b_2 \\ a_3b_1-a_1b_3 \\ a_1b_2-a_2b_1 \end{pmatrix}

Intersection of Lines

•
l=(−1,0,1)Tl = (-1,0,1)^T, l=(0,−1,1)Tl = (0, -1,1)^T
x=l×l′=(111){\rm x} = l \times l' = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}
•
l=(−1,0,1)Tl = (-1,0,1)^T, l=(−1,0,2)Tl = (-1,0,2)^T
x=l×l′=(010){\rm x} = l \times l' = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}
◦
Infinity 에 있는 점을 교점으로 찾아줌! (실제로도 평행한 직선)
•
xx axis 의 vanishing point 는 (1,0,0)T(1, 0, 0)^T, yy axis 의 vanishing point 는 (0,1,0)T(0, 1, 0)^T
[x1x21]×[100]=[01−x2]\begin{bmatrix} x_1 \\ x_2 \\ 1 \end{bmatrix} \times \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \\ -x_2 \end{bmatrix}
◦
임의의 점 (x1,x2,1)T(x_1,x_2,1)^T 과 vanishing point (1,0,0)T(1,0,0)^T 를 지나는 직선은 (0,1,−x2)T(0, 1, -x_2)^T 로, y=x2y=x_2 이고 xx 축과 평행인 직선이 나옴!

Ideal Points and Line at Infinity

•
Ideal points 는 (x1,x2,0)T(x_1,x_2,0)^T 의 형태로 표현이 됨
•
모든 ideal points 는 다음과 같은 Line at Infinity 위에 있음
l∞=(0,0,1)Tl_{\infty}=(0,0,1)^T
◦
(0,0,1)T(x1,x2,0)=0(0,0,1)^T(x_1,x_2,0) =0 이기 때문에 위에 있다는 것을 보일 수 있음

Projective Transformation (Homography)

•
Geometry: transfomations 들에 대해서 invariant 한 특성에 대한 연구
•
2D Projective Geometry: transfomrations 들에 대해서 invariant 한 projective plane P2{\mathbb P}^2 의 특성에 대한 연구
•
Homography 란?
◦
x1,x2,x2\rm x_1, x_2, x_2 가 한 직선 위에 있다면 h(x1),h(x2),h(x3)h({\rm x_1}), h({\rm x_2}), h({\rm x_3}) 도 한 직선 위에 있는, P2\mathbb{P}^2 에서 P2\mathbb P^2 로 이어지는 invertible mapping (Colinearity)
◦
Projectivity == Colineation == Projective Transform == Homography 다 같은 용어
◦
Radial lens distortions 는 non-homography transformations 임
•
3×33\times3 non-singular (invertible) matrix 는 homography 임!
x′=Hx{\rm x'} = \rm H x
◦
H\rm H 는 8 DoF 를 가짐 (up to scale)
◦
Central projection 이 한 예시 (중심점과 ray 를 잇고 원하는 plane 과 만나는 점으로 projection)

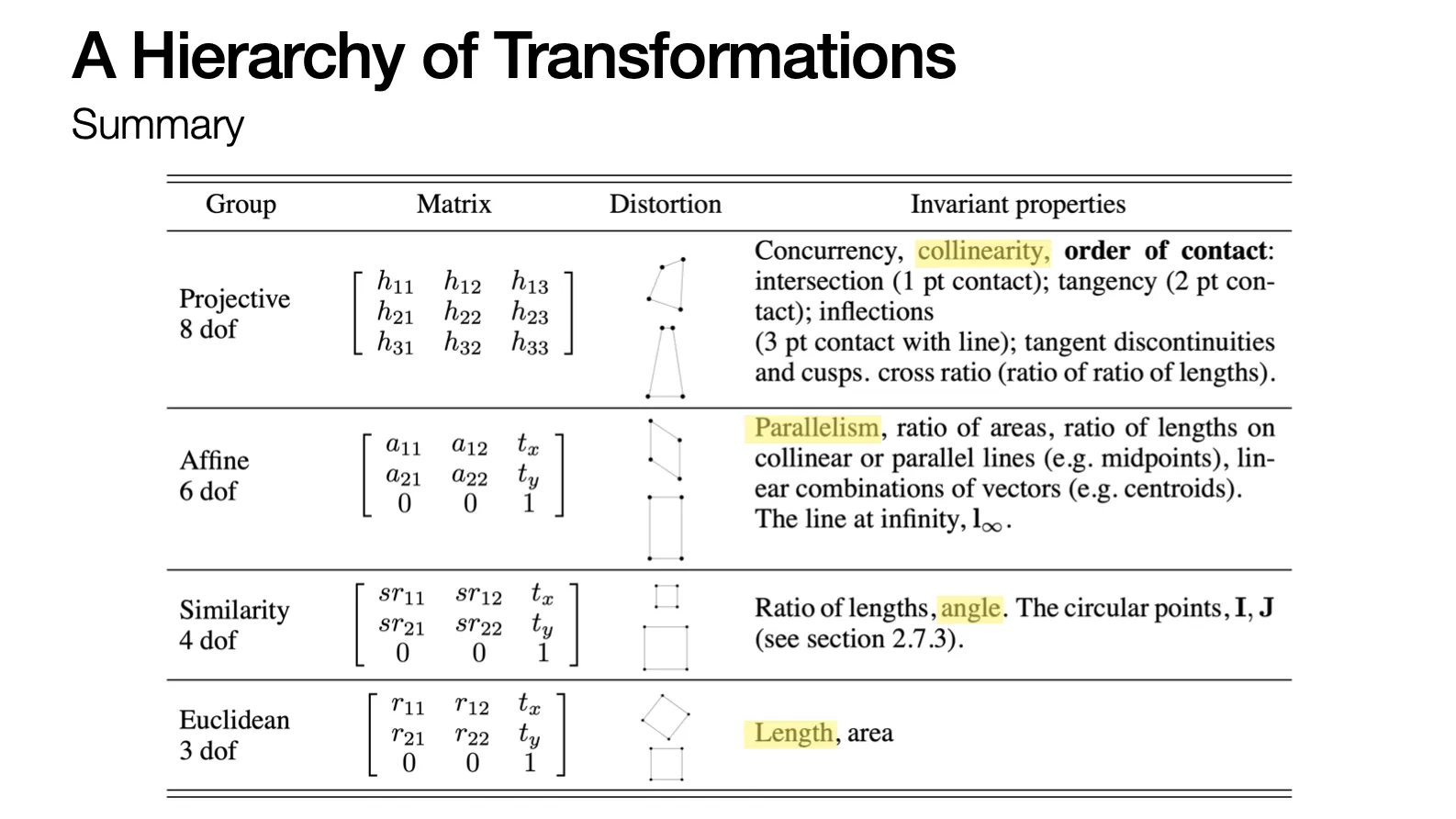
A Hierarchy of Transformations

•
Projective: 8 DoF (line → line, colinearity)
•
Affine: 6 DoF (parallel line → parallel line, parallelism)
•
Similarity: 4 DoF (Rotation with scale + Translation)
•
Euclidean: 3 DoF (Rotation + Translation)

How to Estimate Homography?

•
충분한 수의 corresponding points 가 존재해야 homography 를 찾을 수 있음!
•
Direct Linear Transform
[xi′yi′1]=[h11h12h13h21h22h33h31h32h33][xiyi1]\begin{bmatrix} x_i' \\ y_i' \\ 1 \end{bmatrix} = \begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{33} \\ h_{31} & h_{32} & h_{33} \\ \end{bmatrix} \begin{bmatrix} x_i \\ y_i \\ 1 \end{bmatrix}
x′=h11x+h12y+h13h31x+h32y+h33,  y′=h21x+h22y+h23h31x+h32y+h33,x' = \frac{h_{11}x+h_{12}y +h_{13}}{h_{31}x + h_{32}y + h_{33}}, \thickspace y' = \frac{h_{21}x+h_{22}y +h_{23}}{h_{31}x + h_{32}y + h_{33}},
[xy1−x′x−x′y−x′xy1−y′x−y′y−y′][h11h12h13h21h22h23h31h32h33]=02×1\begin{bmatrix} x & y & 1 & & & & -x'x & -x'y & -x' \\ & & & x & y & 1& -y'x & -y'y & -y' \end{bmatrix} \begin{bmatrix} h_{11} \\ h_{12} \\ h_{13} \\ h_{21} \\ h_{22} \\ h_{23} \\ h_{31} \\ h_{32} \\ h_{33} \\ \end{bmatrix} = 0_{2\times1}
◦
위 식을 여러 개의 x,x′x, x' 쌍에 대해서 켜켜이 쌓아서 8 개의 줄이 생긴다면 HH 는 8 DoF 이기 때문에 구해낼 수 있음 → Non-trivial solution h\rm h 는 null space of A solution 이고 SVD 를 사용해 VV 의 columns 들로 이 null space 를 구해낼 수 있음!
•
Over-determined Solution (4 noisy correspondences 보다 많은 데이터가 있는 경우)
◦
∥Ah∥\|Ah\| 를 최소화하는 hh 를 구하는 문제로 변형 (∥h∥=1\|h\|=1)
◦
A 를 SVD 해서 등장한 VV 의 마지막 column vector (가장 eigenvalue 가 작은 eigenvector)

Homography - Practical Applications

•
Automatically Building Panoramic Images
•
Correspondence 는 SIFT descriptor 로 찾을 수 있음
•
Outlier 의 제거, Inlier 의 판단 등은 RANSAC 으로 진행!