본 포스트에서는 ILSVRC14 에서 2등을 차지한 VGGNet 을 제치고 1등을 한 팀에서 구현한 네트워크에 대해서 살펴보려고 합니다. 리뷰하려는 논문의 제목은 다음과 같습니다.
“Going deeper with convolutions”
Objective
논문의 배경은 Convolutional Neural Network 의 일반적인 형태가 가지는 고질적인 문제점에서부터 시작합니다. LeNet-5 에서부터 시작해서 Convolutional Neural Network 는 "convolutional layer 가 normalization 과 pooling layer 를 optional 하게 가진 형태의 구조가 쌓여 있고, 그 뒤에 fully-connected layer 가 붙어 있는", 일반적으로 좋은 효율을 가진다는 구조로 정형화됩니다.
실제로 위 구조를 기반으로 한 변종들이 MNIST, CIFAR, 그리고 ImageNet classification challenge 에서 좋은 결과를 냈습니다. 특히, ImageNet 과 같이 큰 dataset 의 경우에 논문이 쓰여진 때의 추세는 1. layer 개수 늘리기, 2. layer size 늘리기, 그러면서도 발생할 수 있는 overfitting 을 방지하기 위해서 3. dropout 사용하기 였습니다.
하지만, 이처럼 DNN 의 성능을 개선하기 위해 straightforward 하게 network 의 size 를 늘리는 방법은 크게 두 가지의 단점을 가졌습니다.
첫 번째로, size 가 큰 network 는 많은 parameter 를 가지고 overfitting 에 취약하게 만듭니다. 특히 이는 labeling 된 training data 가 제한적인 경우에 대해서 더욱 심화됩니다.
앞서 말씀드린 dropout 을 사용하면 되지 않겠느냐! 라고 말을 할 수도 있지만, 여기서 말하고자 하는 것은 높은 질의 training data 를 다량 만드는 것은 상당히 어렵고 비용이 많이 들어 간다는 점입니다. 위 사진의 예시처럼 Siberian husky 와 Eskimo dog 는 생김새가 굉장히 비슷한데, 이러한 이미지들을 구별하면서 labeling 을 하는 것은 전문가의 작업을 필요로 합니다.
두 번째로, network 의 size 를 키우면 키울수록 필요한 computational resource 가 기하급수적으로 증가합니다. 실제로 두 개의 convolutional layer 가 연달아 나오게 되면 filter 개수가 일정량 증가했을 때, computation 은 quadratic 하게 증가하게 됩니다.
여기서 quadratic 이라 함은,
실제 제곱의 의미는 아니고 filter 개수가 증가하면 다음 layer 로의 input 개수가 그 만큼 증가하는데, 다음 convolutional layer 에서의 다음 layer 의 filter 수와 증가했던 filter 수의 곱 형태기 때문에 증가량의 배로 증가한다는 느낌으로 보시면 됩니다.
실제 상황에서 computational resource 의 예산은 제한적이기 때문에 무차별적으로 size 를 늘릴 수 없고 효율적인 resource 분배가 필요로 합니다.
위 두가지 방법을 동시에 해결하는 방법으로 논문에서는 fully-connected network 에서 sparsely-connected network 로 바꾸는 방법을 선택합니다. 말 그대로 학습에 불필요한 node 을 삭제해서 실제로 필요한 computation 연산 수와 메모리도 줄이는 것입니다.
이러한 생각은 Arora et al. 에서 처음 등장한 개념으로, 해당 논문에서 설명하는 주요 내용은 dataset 의 확률 분포가 size 가 크고 sparse 한 network 로 표현 가능한 경우에 한해서 CNN 의 마지막 출력과 node 와의 연관관계를 분석하여 연관성이 높은 node 들을 묶음으로써 최적의 network 구조를 얻어낼 수 있다는 점입니다. 물론, 이 내용에 대한 수학적 증명은 엄격한 조건을 전제로 하지만, 논문에서는 이 내용이 잘 알려진 Hebbian Principle 의 맥락과 어느정도 일치한다는 점에서 실제로는 덜 엄격한 조건에서도 적용 가능하다고 보는 것이 가능하다고 이야기 합니다.
여기서 Hebbian Principle 이라 함은,
신경세포학적으로 학습은 뉴런 사이의 새로운 연결이 형성하면서 발생한다라는 사실을 기반으로 한 이론입니다. 어떤 한 뉴런 A가 자극되었을 때의 신호가 뉴런 B 로 전달된다면 두 뉴런 사이의 연결이 생길 가능성이 높아지고, 뉴런 사이의 연결이 생긴다면 뉴런 사이의 신호가 전달될 가능성이 높아진다는 내용 (Fire together, Wire together) 입니다. 이렇게 positive feedback 처럼 진행되다 보면 두 뉴런 사이의 연결이 강해지고 거의 동시에 활성화됩니다.
간단한 예시로, 초콜릿을 먹어본 적이 없는 사람에게 사탕이랑 비슷한 것이라고 지속적으로 이야기를 해주면, 초콜릿에 대한 여러 자극이 주어졌을 때 사탕에 대한 기억이 자꾸 떠오르면서 초콜릿과 사탕의 연결도가 높아집니다. 그러면서 사탕, 초콜릿 둘 중 어느 것에 대한 자극이 와도 서로 다른 것까지로 자극이 이어지게 되는 것입니다.
하지만, 무턱대고 기존 네트워크에서 활성도를 기반으로 연관도가 높은 node 만 취사선택하는 방식으로 network 를 sparse 하게 수정하는 형태로 진행하는 것도 무리가 있습니다. 그 이유는 기존의 컴퓨팅 인프라가 sparse data strucuture 에 대한 효율적인 계산에 적합하지 않기 때문입니다. Sparse data 를 사용할 때의 대수적인 계산 수가 100배 이상 줄었다고 하더라도 lookup miss, cache miss 등의 이유로 실제 효율은 더 낮다고 합니다. (정확한 설명이 없어서 자세히는 모르겠지만, cache 가 무의미한 연산 결과들로 더렵혀졌기 때문이 아닐까 싶습니다.) 특히 dense matrix 에 대한 연산은 꾸준히 발전되고 고도로 튜닝되어 굉장히 발전되고 있지만 sparse matrix 에 대한 연산의 발전은 미비해서 그 차이가 점점 늘어났다고 합니다.
이러한 상황에서 논문에서는 sparse 한 구조를 가지면서도 dense matrix 에서 적용 가능한 연산 방법을 사용할 수 있는 network 에 대해서 고민을 하고 설계하려고 했습니다.
Inception Module
논문에서는 sparse 한 구조를 가지면서도 dense matrix 에서 적용 가능한 연산 방법을 사용할 수 있는 network 로 Inception Module 구조를 제시합니다.
번외로, 이 Inception Architecture 는 논문의 1저자가 앞서 이야기했던 Arora et al. 의 알고리즘으로 형성된 network 의 성능 평가를 하면서부터 발견되어 시작되었다고 합니다.
Optimal 한 network 의 구조를 사용했을 때 정확히 두 번의 iteration 만 거쳐도 기존의 reference 에 비해서 높은 학습 효과를 얻을 수 있었던 것입니다.
물론 이 network 가 computer vision 의 영역에서 성공적인 결과를 가져왔지만, 이 구조가 형성한 알고리즘에 기반한 것인지에 대해서는 확신할 수 없습니다. 하지만, 논문에서는 다른 분야에서도 이와 비슷한 성능 향상을 가져오는 network 를 찾을 수만 있다면 알고리즘에 대한 설득력이 부여될 것으로 보고 있습니다. 이러한 관점에서 논문에서 제시한 Inception Architecture 의 성공적인 결과는 매우 흥미로운 연구 방향성을 제시할 것이라고 주장합니다.
Arora et al. 에서 제시한 network 생성 방법은 layer-by-layer construction 입니다. 마지막 layer 와의 연관성을 기반으로 연관성이 높은 node 들을 clustering 하여 다음 layer 의 구성에 사용하는 방법입니다. 즉 이전 layer 와 연결되는 부분에 clustering 된 node 들이 붙는다고 보시면 됩니다.
이렇게 생성하는 방법에서 이전 layer 의 unit 들은 input image 의 일부 영역을 의미하고, 뒤쪽에 새로 붙게 되는 layer 는 filter bank 로 해석할 수 있습니다. 이 때, input 과 가까운 쪽의 layer 들은 local 한 영역에서 cluster 들이 concentrate 되어 있고, 이는 다음 layer 에 convolutional layer 를 두는 것으로 구현할 수 있습니다. 하지만 적은 수의, 공간적으로 퍼져 있는 cluster 들이 존재할 수 있고, 이는 convolutional layer, convolutional layer 등의 큰 patch size 의 convolution layer 로 구현할 수 있습니다.
홀수 convolutional layer 만을 사용한 것은 patch 의 중심을 잡기 용이하기 때문입니다. 특정 pixel 을 기준으로 그 주변 영역의 연관도까지 보기 위해서 convolution 이 존재하는 것인데 짝수 convolutional layer 를 선택하면 대칭적으로 주변을 선택할 수 없기 때문입니다. 이를 patch alignment issue 라고 합니다.
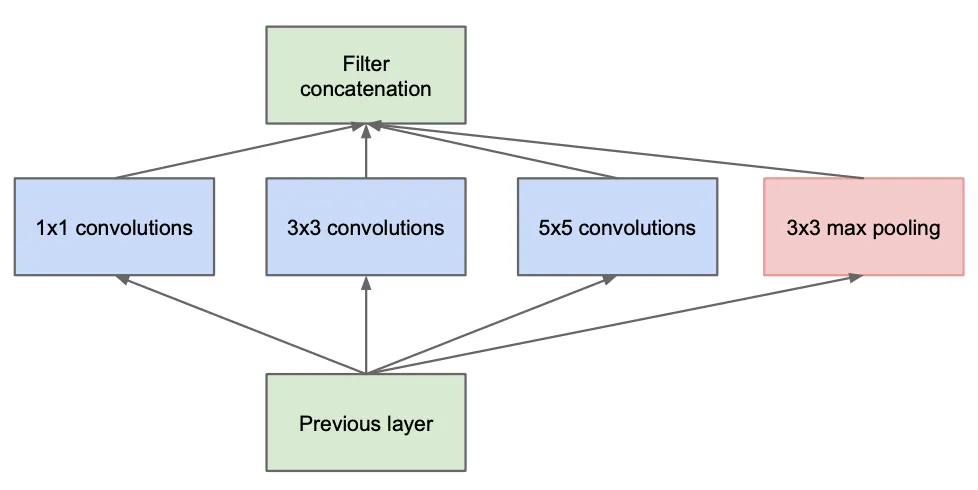
결과적으로, concentrate 되어 있는 cluster 와 그렇지 않고 spread out 되어 있는 cluster 에 대한 구현을 모두 포함하기 위해서 해당 convolutional layer 의 output vector 가 하나의 vector 를 형성하는 layer 들의 combination 을 구현한다는 생각까지 도달한 것입니다.
그렇게 구현한 Inception Module 은 위와 같은 모습입니다. 이전 layer 에 각각의 convoulution layer 가 병렬적으로 이어붙인 형태에 max-pooling layer 가 추가적으로 붙은 모습입니다. Max-pooling layer 의 추가는 당시의 SOTA CNN 이 pooling operation 으로 큰 성능적인 이득을 보았기 때문에 추가한 것이라고 합니다. 실제로 위와 같이 병렬적인 구조로 설계를 한 뒤 살펴본 마지막 layer 와의 연관도에 대한 통계는 집중되어 있는 부분과 퍼져 있는 부분이 다양하게 나타났다고 합니다.
하지만, 설계한 Inception Module 에도 생각보다 큰 문제가 있었습니다. convolutional layer 가 적절한 수준으로 존재했는데도 불구하고 filter 의 개수가 많으면 output 의 개수도 그만큼 많아지기 때문에 겉잡을 수 없이 이후의 계산 비용이 증가했습니다. 이러한 문제를 해결하기 위해 논문에서는 Inception Module 에 약간의 수정을 가합니다.
Inception Module + Dimension Reduction
논문에서는 신중하게 dimension reduction 을 사용해서 과도한 연산을 막으려는 시도를 합니다. 실제로 많은 양의 데이터를 포함하고 있는 저차원의 embedding 이 성공적으로 존재한다는 사실에 기반하여 데이터의 압축을 시도한 것입니다. 이 때 연산량을 줄이기 위해서 convolutional layer, convolutional layer 의 전에 미리 개수가 적은 convolutional layer 를 두어 output channel 수를 획기적으로 줄이는 형태로dimension 을 줄여놓는 방법을 택합니다.
위에서 설명드린 내용이 반영된 모습이 위 그림입니다. 위 그림이 dimension reduction 이 적용된 하나의 Inception Module 로 볼 수 있고, 실제로 GoogLeNet 은 위 모듈이 쌓여있는 구조입니다. 실제로는 메모리 효율성의 문제로 input 과 먼 쪽부터 Inception Module 이 등장하고, 가까운 쪽에는 전통적인 CNN 의 모습을 가지고 있는 구조를 성계했다고 합니다.
논문에서 정리하는 Inception Module 이 가지는 장점은 크게 두 가지입니다.
1.
Computational complexity 의 급격한 증가 없이 stage 수 및 각 stage 에 속하는 unit 수를 증가시킬 수 있습니다.
특히, dimension reduction 의 사용으로 다음 stage 로 이동하기 전에 먼저 dimenstion 을 줄이고 convolution 을 거치는 형태로 다음 stage 에 큰 size 의 input 이 들어가는 것을 방지했습니다.
2.
이미지로부터 시각 정보를 추출할 때 다양한 scale 로 봐야한다는 직관과 통하는 구조를 가지고 있습니다.
다양한 크기의 convolutional layer 를 병렬적으로 사용하면서 이미지 정보를 가져오는 범위를 다양화하고 해당 정보를 모두 합쳐서 사용했습니다.
여기까지 읽었을 때 저는 굉장히 혼란스러웠습니다.
논문에서 제기한 문제점과 논문에서 구현한 구조와의 연관성에 대한 설명이 부족했기 때문입니다. 논문에서 제기한 문제 상황은 한 마디로 computation 의 대수적인 수 자체를 줄이려면 sparse 해야 하는데 막상 sparse 한 데이터의 연산은 computationally expensive 한 상황입니다.
그런데, 논문에서 제시한 구조를 설명할 때는 마지막 layer 와의 연관성을 기반으로 한 알고리즘으로 생성했고 연관성이 높은 cluster 를 표현할 layer 를 설정하다보니 해당 구조가 나왔습니다.
그래서, 논문의 구조가 해당 문제 상황을 어떻게 해결할 수 있는지에 대한 내용을 찾아보았습니다. 관련해서 Inception Module 의 병렬적 구조가 실제로 학습 시에 병렬적으로 처리되기 때문에 하나의 path 기준으로 바라보았을 때 나머지 path 가 inactivate 되어 전체적으로 보았을 때 sparse 하다는 사실을 알 수 있었습니다. 그렇지만 또 하나의 path 를 보았을 때는 상대적으로 dense 하기 때문에 기존의 dense matrix 에 적용하던 연산을 무리 없이 적용할 수 있었던 것입니다.
GoogLeNet
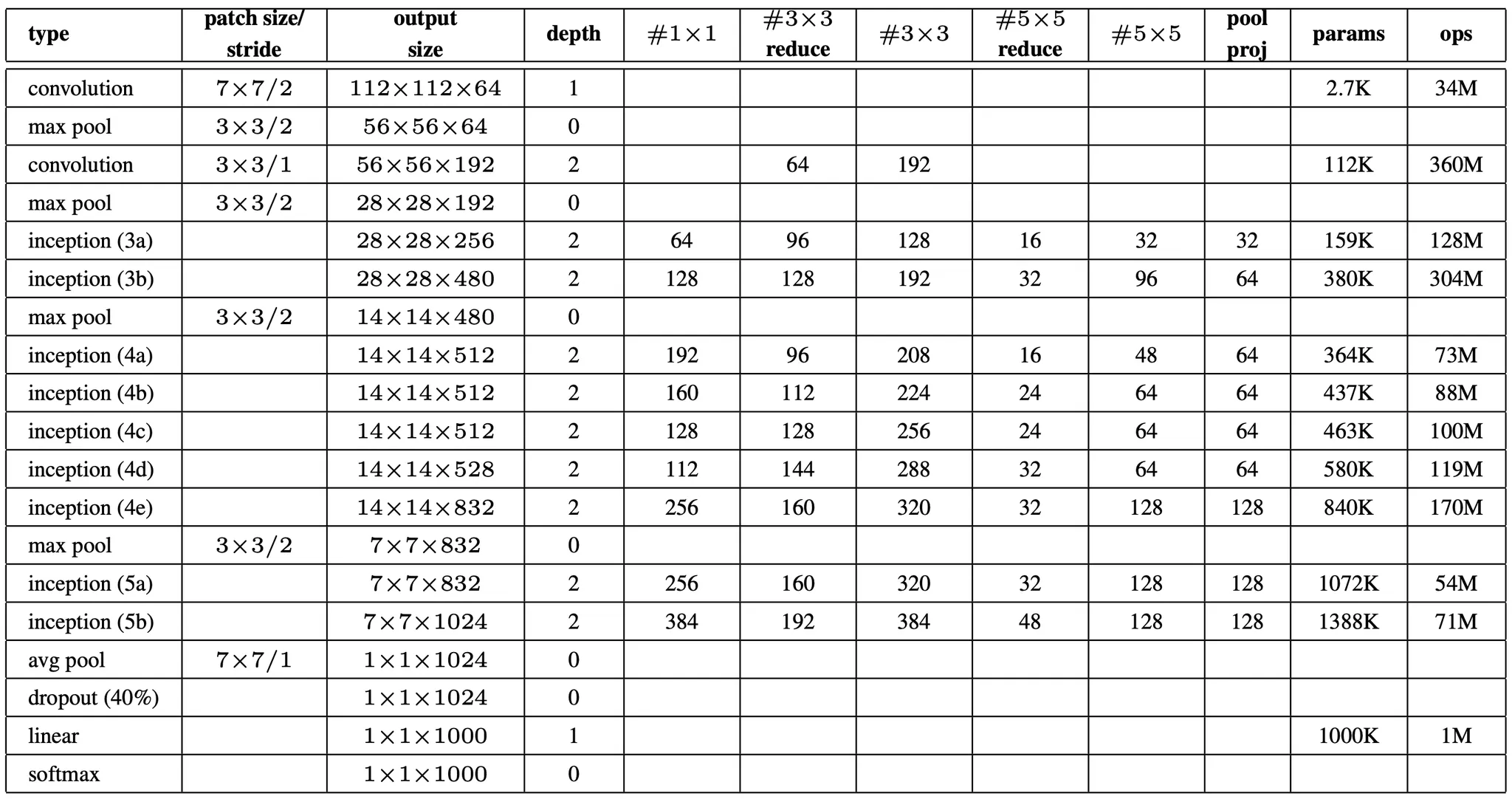
논문에서는 앞서 설명드린 Inception Module 을 사용하여 GoogLeNet 을 설계했습니다. GoogLeNet 은 LeNet-5 를 구현한 LeCuns 에 대한 존경으로 이름을 붙이게 되었고 ILSVRC14 의 우승작이 되었습니다. 특히, 우승작 출품 때는 가장 성공적이었던 아래와 같은 network 구성을 사용했습니다.
논문에서는 위 구성에 대한 설명을 진행하는데, 이를 간단하게 나열식으로 소개드리려고 합니다.
1.
모든 convolution 은 ReLU 를 포함하고 있습니다.
2.
Input image size 는 에 RGB 3개의 channel 을 가집니다.
3.
와 는 각각 dimension reduction 을 위해서 convolution layer, convolution layer 이전에 사용한 convolution layer 의 filter 개수입니다.
4.
는 max pooling layer 이후에 사용한 convolution layer 의 filter 개수입니다.
5.
parameter 가 존재하는 layer 만 세면 전체 22 layer 이고, pooling 까지 세면 27 layer 입니다.
6.
전체 layer 의 수는 100 개 정도이지만 이는 사용한 ML 인프라에 따라 상이할 수 있습니다.
7.
마지막 classification 을 하기 전에 average pooling layer 를 사용한 것은 Lin et al. 에 기반한 구현입니다. Fully-connected layer 를 사용할 때보다 다른 labeling set 으로 fine-tuning 할 때 더욱 용이하지만 편의성일 뿐 주요 원인으로 보고 있지는 않다고 합니다. 또한 이 교체가 top-1 accuracy 를 0.6 % 정도 개선했다고 합니다.
이렇게 완성된 GoogLeNet 의 모습은 아래와 같습니다.
그림만 봐도 상당히 긴 것을 볼 수 있습니다. 이렇게 깊은 network 는 고질적으로 나타나는 문제가 있습니다. 앞선 ResNet 등에서도 살펴본 gradient vanishing 이 그것입니다. GoogLeNet 도 예외는 아니었고, gradient 가 layer 를 거쳐서 propagate 되지 않는 이슈를 해결하기 위해서 특별한 구조를 고안하게 됩니다.
Auxiliary Classifier
논문에서 gradient vanishing 문제를 해결하기 위해서 auxiliary classifier 라는 구조를 설계합니다. 이름 그대로 classification 에 도움을 주는 추가적인 classifier 를 설계에 추가한 것입니다.
기존의 gradient vanishing 은 output 으로부터 먼 곳의 gradient signal 이 굉장히 미비하게 전달된다는 점이었습니다. 이를 해결하기 위해 input 에 가까운 두 곳 정도에 추가적으로 classifier 를 설치하여 상대적으로 input 에 가까운 곳의 gradient 에 가중치를 두어 학습할 수 있도록 하는 것입니다. 가중치를 주는 방법은 최종적인 loss 의 계산에 두 classifier 에서 나타난 loss 를 0.3 만큼 가중치를 두어 반영하는 것입니다. 이는 곧, input 에 가까운 weight 가 loss 에 기여하는 정도를 늘림으로써 gradient vanishing 의 효과를 어느정도 완화하는 것입니다.
이렇게 구현한 위의 그림에서 살펴볼 수 있듯이 auxiliary classifier 는 Inception Module (4a), (4d) 의 output 의 꼭대기에 위치해 있습니다. 이 구조는 학습하는 동안 gradient vanishing 의 효과를 줄이기 위해 사용하는 것이기 때문에 실제로 학습 후에 추론하는 단계에서는 사용하지 않습니다.
논문에서는 추가로 auxiliary classifier 의 구성에 대한 설명을 진행하는데, 이는 간단하게 나열식으로 소개드리려고 합니다. 논문의 주요 내용을 이해하기 위해서 크게 필요한 내용은 아닌 것 같아서 간단하게 훑어보고만 지나가셔도 좋을 것 같습니다.
1.
Average pooling layer 를 filter size, stride 3 으로 사용했습니다.
그 결과 (4a) 에서는 형태의 vector 가 output 으로, (4d) 에서는 형태의 vector 가 output 으로 나오게 되었습니다.
2.
convolutional layer 는 128 개의 filter 를 사용했으며, 마찬가지로 dimension reduction 과 ReLU activation 의 효과를 보기 위함입니다.
3.
Fully-connected layer 는 1024 개의 unit 과 ReLU 를 가지고 있습니다.
4.
Dropout 으로 0.7 을 사용했습니다.
5.
Linear layer 에 softmax 를 사용하여 1000 class 를 예측합니다.
Training Methodology
지금까지 논문에서 설계한 network 의 구조에 대해서 알아보았습니다. 여기서는 논문에서 사용한 학습 방법에 대해서 소개를 드리려고 합니다. 이 부분도 사실 논문에서 실제로 구현의 구체성을 위해서 제시한 부분이기 때문에 크게 중요하지는 않아보여서 간단히 보고 넘어가셔도 좋을 것 같습니다. 편의상 나열식으로 설명드리려고 합니다.
1.
DistBelief 라는 적절한 모델과 data-parallelism 을 제공하는 distributed ML system 을 사용했습니다.
2.
CPU based implementation 만 진행했습니다.
다만, 대강 예측하기로 high-end GPU 를 사용해 수렴까지 학습하는데 일주일 정도로 보고 있습니다.
이 때 주요 제약은 메모리였습니다.
3.
Asynchronous SGD 와 0.9의 momentum 을 사용했습니다.
4.
매 8 epoch 마다 4% 씩 감소하는 learning rate 라는 고정된 schedule 을 사용했습니다.
5.
마지막 Model 을 만드는 데에 Polyak Averaging 을 사용했습니다.
Polyak Averaging 은 학습하는 동안의 parameter 를 저장해 둔 후 평균을 하는 방법입니다.
를 통해 구할 수 있습니다.
6.
ILSVRC14 를 진행하는 동안 image sampling 방법과 sampling size 를 바꾸었고, 그것과 동시에 hyper parameter 와 learning rate 를 바꾸었기 때문에 학습에 가장 효과적인 방법을 가이드하는 것은 어렵다고 합니다.
7.
ILSVRC14 이후에는 이미지의 전체 크기가 8% ~ 100% 사이에 고르게 분포되고 가로/세로 비율이 구간 내에서 무작위로 sampling 되었을 때 학습 효과가 좋다는 것을 발견했습니다.
8.
Andrew Howard 의 photometric distortion (밝기, 대조, 값 조정)은 overfitting 을 해결하는데 큰 도움이 되었습니다.
9.
Resizing 할 때 사용할 보간법으로 Random Interpolation Method 를 사용했는데, 6번에서와 마찬가지로 hyperparameter 의 교체와 같이 사용하여 결과에 영향을 미쳤는가에 대해서는 확답할 수 없다고 합니다.
ILSVRC 2014 Classification Challenge
ILSVRC 2014 Classification Challenge 는 ImageNet 의 1000 개의 카테고리를 분류하는 작업을 진행하는 것이었습니다. Training dataset 120만개, validation dataset 5만개, 그리고 test dataset 10만개를 제공하여 대회를 진행했습니다. 주로 top-1 accuracy 와 top-5 accuracy 를 evaluation metric 으로 사용하는데 이 대회에서는 top-5 accuracy 로 등수를 매겼습니다.
논문에서는 학습효과를 극대화하기 위해서 다음과 같은 작업들을 진행합니다.
1.
Sampling methodology 와 input order 만 다른 7가지 버전의 GoogLeNet 을 학습하여 ensemble 을 진행했습니다. (다수의 모델이 꼽은 class 로 classify 하는 방법론)
2.
Image Cropping 을 할 때 상당히 적극적인 방법을 사용합니다. 그 방법은 다음과 같습니다.
a.
먼저, 이미지의 가장 짧은 변이 256, 288, 320, 그리고 352 pixel 이 되도록 resizing 합니다.
b.
다음으로, resizing 된 이미지를 좌측, 중간, 우측으로 정사각형 형태로 자릅니다. 이 때 정사각형의 변의 길이는 이전에 resizing 한 짧은 변 길이랑 같게 됩니다.
c.
이후, 전체 각 정사각형마다 정사각형 본인, 각 모서리 4개, 중앙 까지 해서 6개의 정사각형으로 자른 뒤 resizing 합니다.
d.
위에서 구한 이미지들의 대칭 버전도 dataset 에 포함합니다.
위 방법을 진행하면 하나의 이미지를 가지고 개의 잘려진 input image 를 생성할 수 있게 됩니다.
3.
최종 결과는 2번에서 생성한 잘려진 이미지들을 가지고 1번에서 구성한 다양한 classifier 를 가지고 softmax probabilities 를 평균하여 산출합니다. 논문에서는 validation data 로 잘려진 이미지들에 대한 max pooling 한다거나 classifier 결과를 averaging 한다는 등의 방법 등을 검증해보았는데, 기존 simple averaging 방법이 제일 좋았다고 합니다.
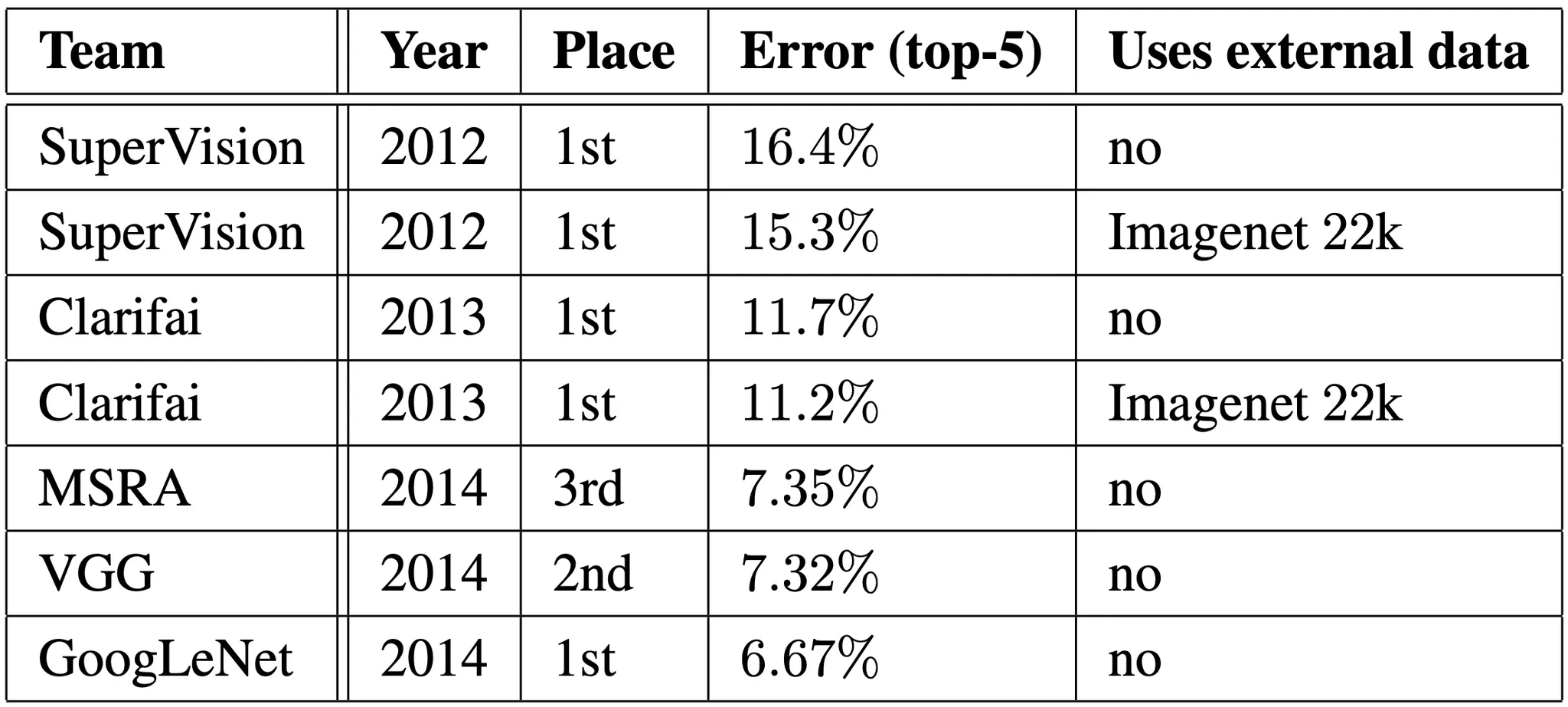
위와 같은 방법으로 진행한 학습에서, 논문은 다음과 같은 결과를 얻습니다.
논문의 network 인 GoogLeNet 은 test dataset 과 validation dataset 모두에서 6.67% 의 top-5 accuracy 를 얻습니다. 이는 2012 년도에 1등을 했던 external data 를 사용한 Supervision 에 비해서 56.5%, 2013 년도에 1등을 했던 external data 를 사용한 Clarifai 에 비해서 40% 의 개선을 이룬 것입니다.
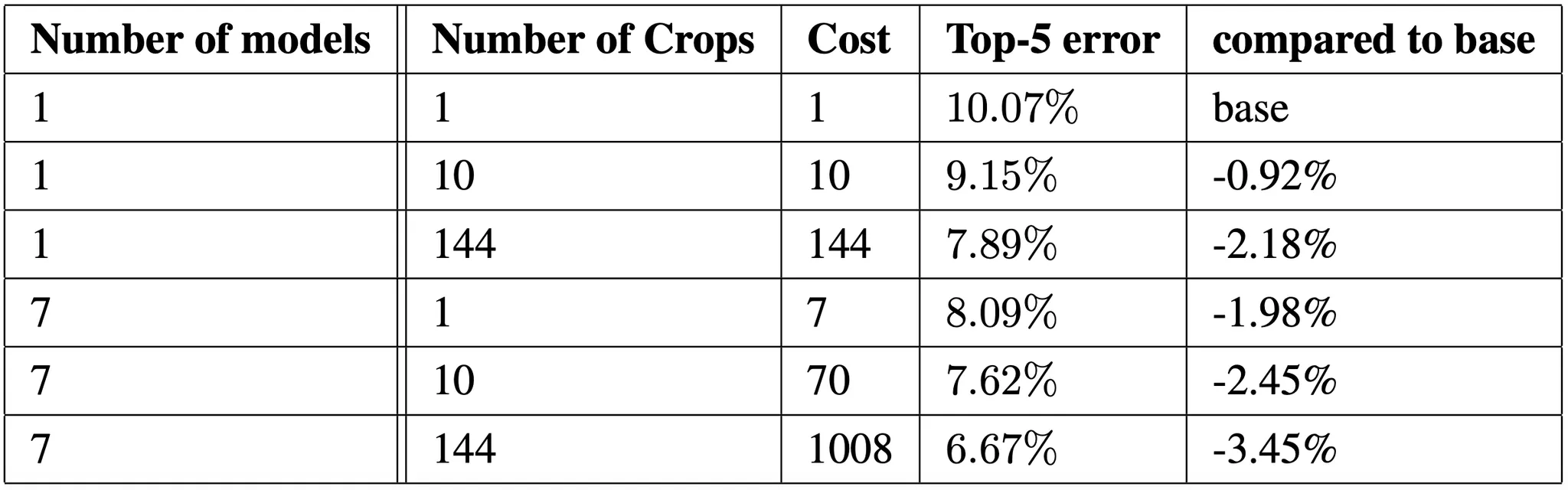
다음으로 논문에서는 다양한 조건 내에서 GoogLeNet 을 변화시켜가며 성능을 비교한 표를 제시합니다. 논문에서는 실제로 ensemble 관점에서의 Model 수, Image crop 의 개수 등을 조절해보았고, 그 결과 가장 낮은 top-5 error 를 얻은 7개 + 144개의 crop 을 사용한 것입니다.
ILSVRC 2014 Detection Challenge
ILSVRC 2014 Detection Challenge 는 ImageNet 의 200 개의 카테고리에 대한 bounding box 를 그리는 작업을 진행하는 것이었습니다. 대회에서는 정확한 class 를 예측하고 bounding box 가 50% 이상 겹쳐지면 성공적으로 detect 한 것으로 보았습니다.
50% 이상 겹쳐진다를 어떻게 정의할까요?
논문에서는 Jaccard Index 를 사용한다고 알려주었습니다. Jaccard Index 는 두 집합이 얼마나 겹쳐지는 가를 산출하는 지표로, 합집합에 대한 교집합의 비율로 볼 수 있습니다.
수식으로 표현하자면 로 볼 수 있습니다.
Classification Challenge 와는 달리 같은 Detection Challenge 에서는 mAP 를 evaluation metric 으로 사용합니다. mAP 에 대한 설명은 이전에 진행했던 리뷰를 참고해주세요.
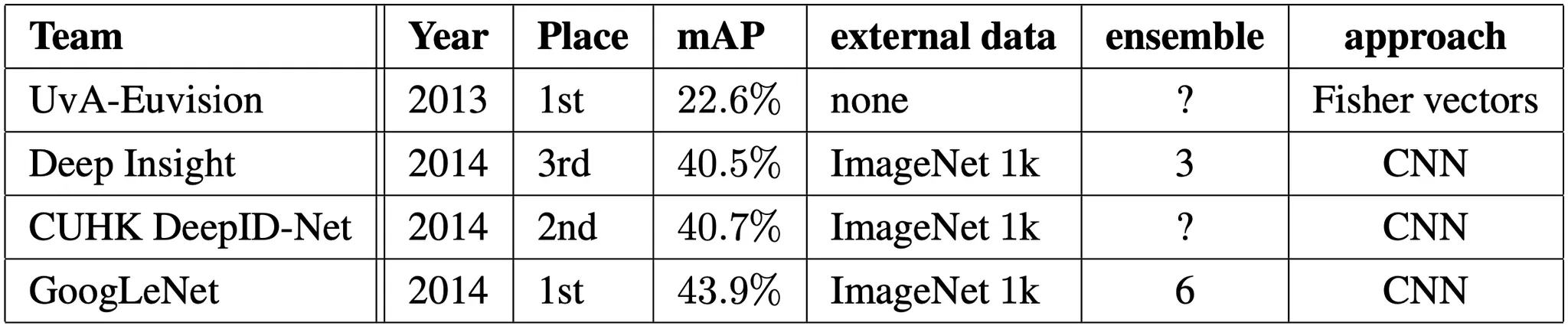
GoogLeNet 이 detection 에 사용한 접근법은 R-CNN 과 동일하지만, Inception Module 을 통해 그 기능을 강화했다고 볼 수 있습니다. 특히, R-CNN 에서 나타난 Selective Search 단계 (segmetation 이후에 이들을 모아 가면서 region proposal 을 형성하는 방법) 를 multi-box prediction 과 결합하여 개선함으로써 recall 을 높였다고 합니다. 추가로 False Positive 의 수를 줄이기 위해서 superpixel (pixel 의 묶음 단위) 크기를 2배 증가시켰고 이를 통해서 Selective Search 단계에서 얻어지는 proposal 의 수가 반으로 줄었다고 합니다. 이것에 multi-box prediction 으로 나온 200 개 정도의 proposal 을 더해 총 proposal 은 R-CNN 에서 사용한 것의 60% 정도이지만, 이러한 접근은 coverage 는 92% 에서 93% 로 올랐다고 합니다. 최종적으로 6개의 CNN 에 대한 ensemble 을 사용하여 40% 에서 43.9% 로 mAP 를 향상시킬 수 있었고 1등을 차지하게 됩니다.
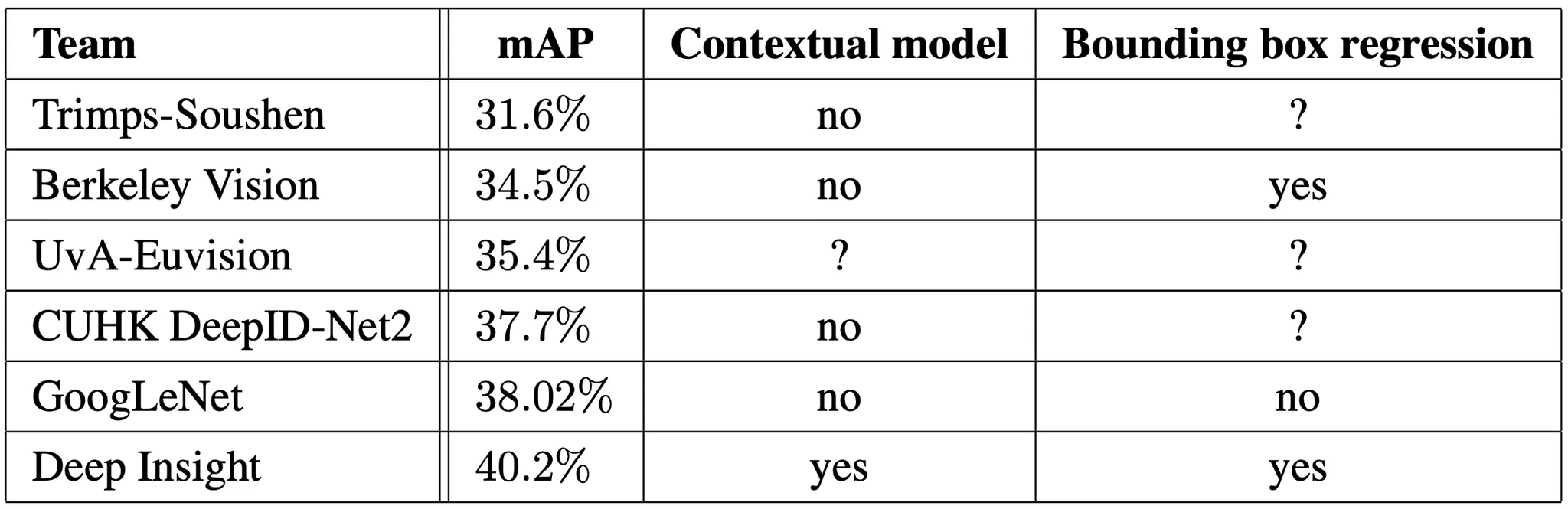
다음으로 논문에서 제시한 것은 단일 ensemble 을 제외한 단일 모델에 대한 지표입니다. 1등을 차기한 것은 Deep Insight 인데 주목할 점은 ensemble 로 0.3% 의 mAP 정도밖에 확보하지 못헀다는 점입니다. GoogLeNet 은 이것에 비교해서 확연한 상승을 볼 수 있었습니다.
Conclusion
이것으로 논문 “Going deeper with convolutions” 의 내용을 간단하게 요약해보았습니다.
VGGNet 논문을 읽을 때 ILSVRC 14에서 1등을 하지 못하고 2등을 했다길래 1등이었던 GoogLeNet 을 눈여겨보고 있다가 이번 기회에 한 번 읽어보았습니다. 논문에서 전달하는 바에 대한 개연성이 중간에 이해가 안되서 많이 답답했던 부분이 있었던 것 같습니다. 전체적으로 맥락 자체는 이해해도 흐름을 이해하기에는 조금 어려웠던 논문이었던 것 같고 논문 작성자의 지식 폭이 확실히 드러나는 논문이 아니었나 싶습니다.
이 논문도 Computer Vision 에 관심이 있으신 분들은 꼭 읽어보시는 것을 추천드립니다.