Duplicate

Lecture 18 | Shape from Shading

수강 일자
2023/03/05

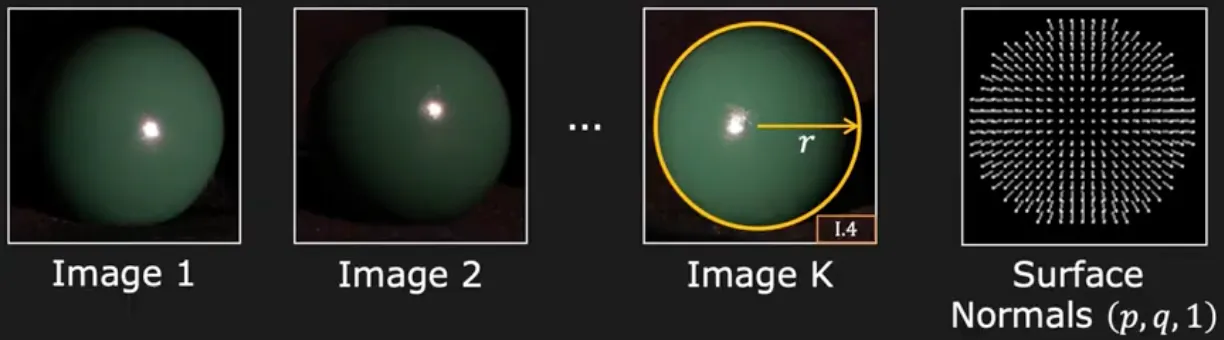
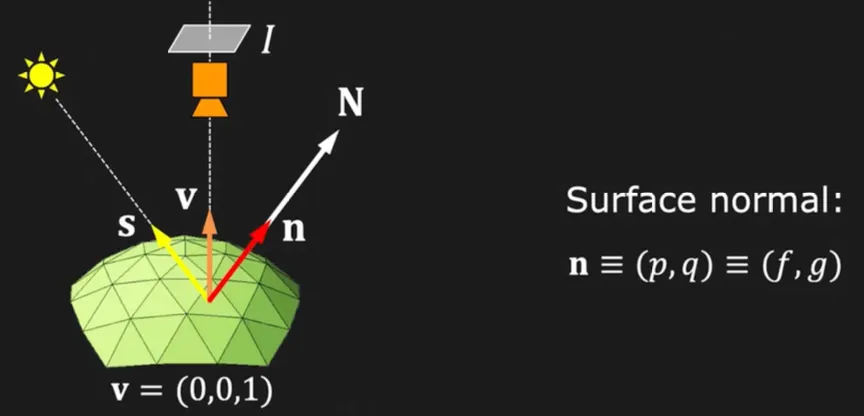
Calibration Based Photometric Stereo

•
Calibration Sphere 는 이미 Surface Normal 을 알고 있는 물체임.
•
Sphere 같은 물질로 이루어진 다른 물체를 같은 Light Condition 에서 본 이미지가 주어졌을 때 동일한 Surface Normal 을 가지는 부분의 rightness 는 동일할 것이므로, 이를 통해 모르는 물체의 Surface Normal 을 구해낼 수 있음.
•
Calibration Sphere 를 다른 Lighting Condition 에서 K 장의 이미지를 얻어내고 각 이미지에서 같은 위치에 있는 점들의 brightness tuple 과 그에 해당하는 Surface Normal 값을 mapping 하는 look-up table 을 구성할 수 있음.
•
새로운 물체에 대해서 동일한 Lighting Condition 에서 K 장의 이미지를 얻어내고 각 이미지에서 같은 위치에 있는 점들의 brightness tuple 을 얻어내고 look-up table 에서 해당 tuple 과 대응되는 Surface Normal 값을 찾아 픽셀에 대응시킬 수 있음.

Shape from Shading

•
Shading 기반의 Single Image 를 활용하여 3D information 을 재구성하는 과정
•
Photometric Stereo 에서 살펴본 바와 같이 기본적으로 brightness 를 가지는 픽셀은 각도만을 알 수 있고 정확한 위치는 알 수 없기 때문에 surface normal 을 구하는데 ambiguity 가 존재하고, 결과적으로 Shape from Shading 은 Ill-posed problem 임.
•
이러한 Ill-Pose Problem 을 해결하기 위해 다음과 같은 가정을 도입함.
1.
Infinity Point Light Source (ss is independent of geometry / depth)
2.
Infinity Camera Position (no distorsion)
3.
Shape is changing smoothly - Normal is changing smoothly
4.
Lambertian Model

Human Perception

•
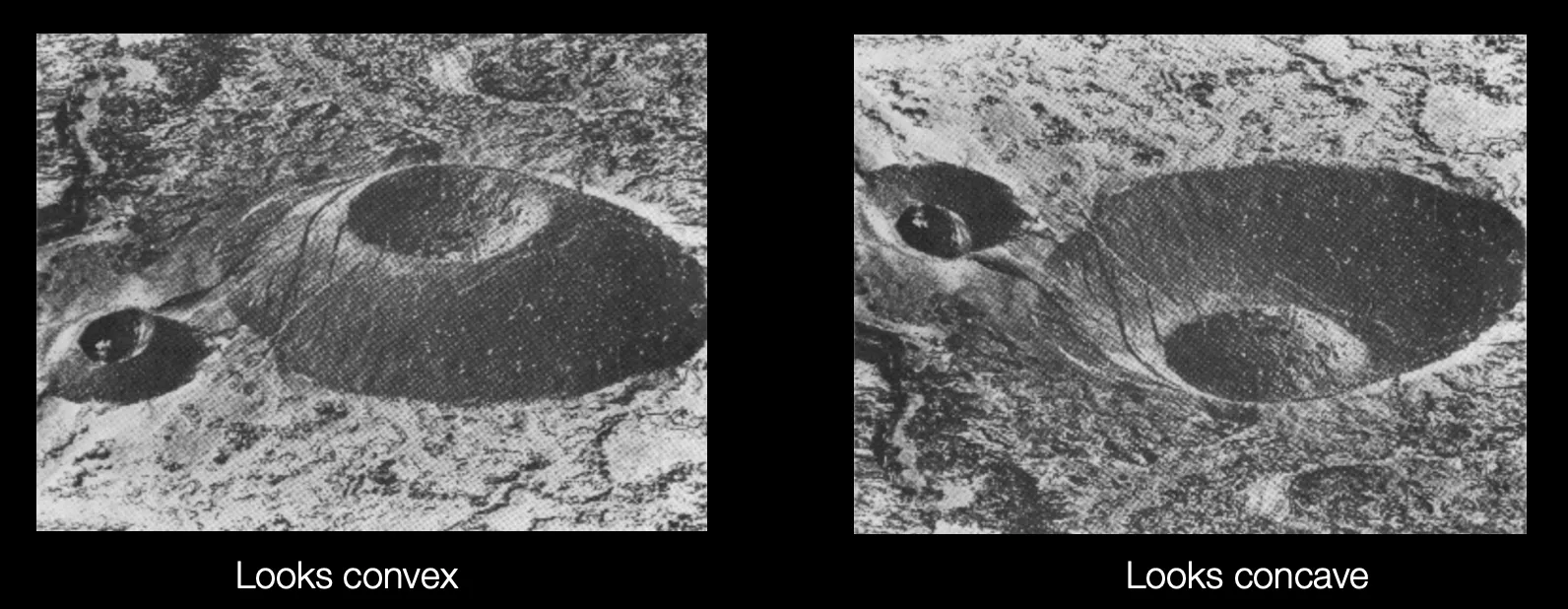
우리의 뇌는 Shading 으로부터 Shape 을 지각해낼 수 있음.
◦
우리의 뇌는 Light 이 위에서 오는 것에 익숙하고 biased 되어 있음.
◦
우리의 뇌는 Occluding Contour 에 biased 되어 있음.
•
중요한 점은, 인간은 Shading 으로 (맞을지는 모르지만…) 불완전한 정보를 예측해낼 수 있다는 것임.

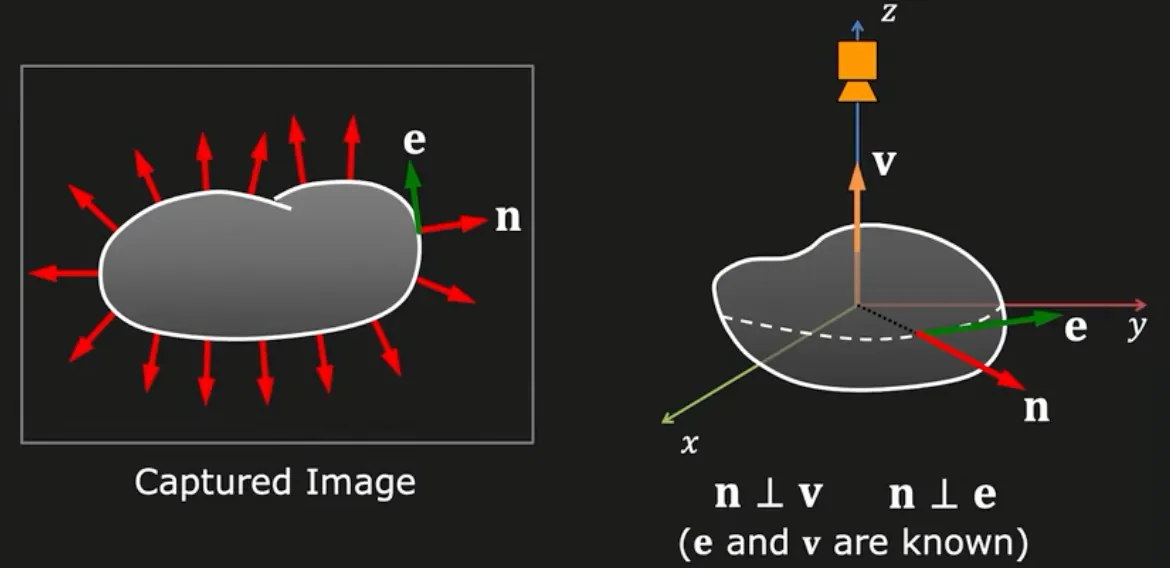
Occluding Boundaries

n=e×v{\rm n} = {\rm e} \times {\rm v}
•
이미지 속 물체의 boundary 부분의 normal 은 view direction (vv) 과 tangential line (ee) 모두에 수직인 방향임을 가정할 수 있음.

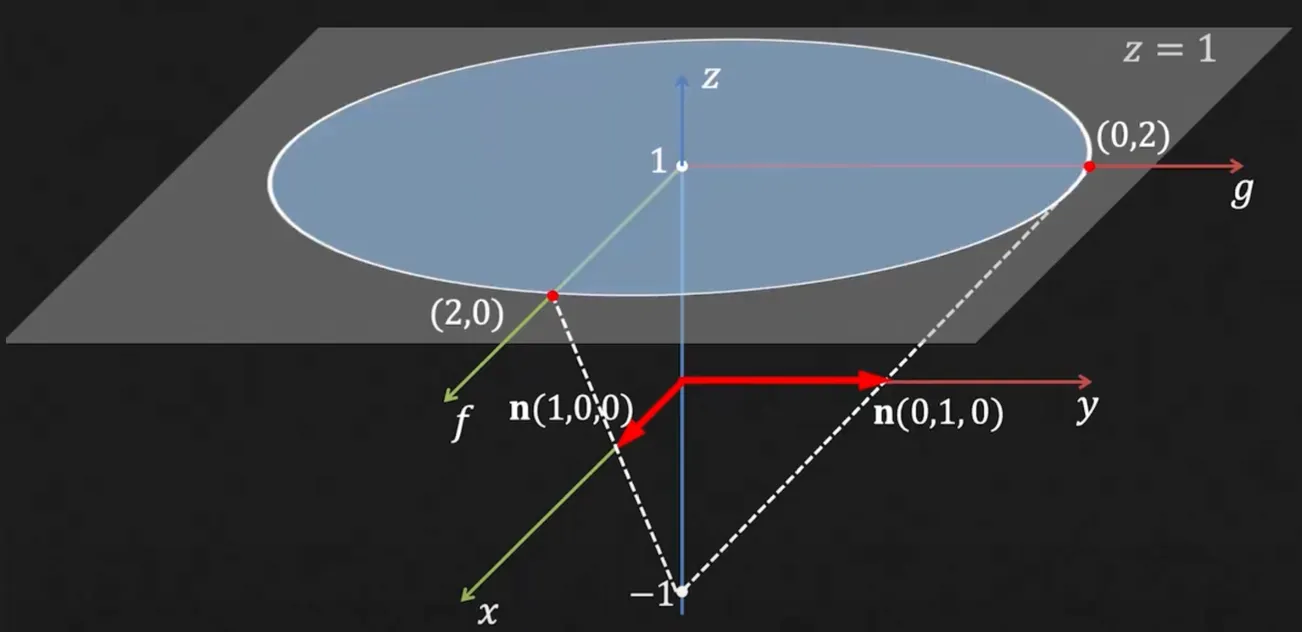
Stereographic Projection: fg Space

f=2p1+p2+q2+1g=2q1+p2+q2+1f = \frac{2p}{1+\sqrt{p^2+q^2+1}} \\ g = \frac{2q}{1+\sqrt{p^2+q^2+1}}
•
(0,0,−1)(0,0,-1) 지점에서 surface normal vector 의 끝과 연결해 z=1z=1 과 생성하는 교점을 (f,g)(f,g) 로 하여 새롭게 parametrize 할 수 있음.
•
이러한 parametrization 이 좋은 이유는, 모든 가능한 normal vector 를 반지름이 2 인 원 위로 제한할 수 있기 때문임.

Reflectance Map R(f,g)R(f,g)

I=Rs(f,g)I=R_s(f,g)
•
Photometric Stereo 에서 등장했던 것처럼 f,gf,g 가 주어지면 p,qp, q 를 알 수 있고 normal direction 을 알 수 있음. 여기에 source direction vector ss 까지 알면 II 를 구할 수 있음.

Image Irradiance Constraint

er=∫∫(I(x,y)−Rs(f,g))2dxdye_r = \int\int(I(x,y)-R_s(f,g))^2dxdy
•
Image Intensity 는 Reflectance Map 과 동일해야 함.
•
위의 식을 최소화함을 통해 Reflectance Map 을 최적화할 수 있고, 최종적으로 f,gf, g 및 normal direction 을 최적화할 수 있는 것임.

Smoothness Constraint

es=∫∫(fx2+fy2)+(gx2+gy2)dxdywhere: fx=∂f∂x, fy=∂f∂y, gx=∂g∂x, gy=∂g∂ye_s=\int\int(f_x^2 + f_y^2)+(g_x^2 + g_y^2)dxdy \\ \quad \\ {\rm where:}\ f_x=\frac{\partial f}{\partial x},\ f_y=\frac{\partial f}{\partial y},\ g_x=\frac{\partial g}{\partial x},\ g_y=\frac{\partial g}{\partial y}
•
Object Surface 의 smoothness 를 가정하면 f,gf,g 의 gradient values 가 천천히 변해야 함.

Shape from Shading + Numerical Shape from Shading

e=es+λere = e_s +\lambda e_r
•
위 식을 최소화하는 모든 픽셀 점들에 대한 (f,g)(f,g) 의 집합을 구해 각 픽셀에서의 Surface Normal 을 계산할 수 있음.
•
Numerical 하게는 각 픽셀 (i,j)(i,j) 에 대해 error term 은 다음과 같이 계산이 가능함.
esi,j=14((fi+1,j−fi,j)2+(fi,j+1−fi,j)2+(gi+1,j−gi,j)2+(gi,j+1−gi,j)2)eri,j=(Ii,j−R(fi,j,gi,j))2e_{si,j} = \frac{1}{4}((f_{i+1,j}-f_{i,j})^2 +(f_{i,j+1}-f_{i,j})^2 +(g_{i+1,j}-g_{i,j})^2 + (g_{i,j+1}-g_{i,j})^2) \\ e_{ri,j} = (I_{i,j}-R(f_{i,j},g_{i,j}))^2
•
최종적인 error 는 다음과 같음.
e=∑i∑j(esi,j+λeri,j)e = \sum_i\sum_j (e_{si,j} + \lambda e_{ri,j})
•
이 때 (fk,l,gk,l)(f_{k,l}, g_{k,l}) 이 ee 를 최소화하면, ∂e∂fk,l=∂e∂fk,l=0\frac{\partial e}{\partial f_{k,l}} = \frac{\partial e}{\partial f_{k,l}} = 0 이 성립합.
◦
특정한 fi,j,gi,jf_{i,j}, g_{i,j} 는 summation 에서 4 개의 항목에서 나타남.
∂e∂fk,l=2(fk,l−fˉk,l)−2λ(Ik,l−Rs(fk,l,gk,l))∂Rs∂f=0∂e∂gk,l=2(gk,l−gˉk,l)−2λ(Ik,l−Rs(fk,l,gk,l))∂Rs∂g=0where fˉk,l=14(fk+1,l+fk−1,l+fk,l+1+fk,l−1)gˉk,l=14(gk+1,l+gk−1,l+gk,l+1+gk,l−1)\frac{\partial e}{\partial f_{k,l}} = 2(f_{k,l} - \bar{f}_{k,l})-2\lambda(I_{k,l}-R_s(f_{k,l},g_{k,l}))\frac{\partial R_s}{\partial f} = 0 \\ \frac{\partial e}{\partial g_{k,l}} = 2(g_{k,l} - \bar{g}_{k,l})-2\lambda(I_{k,l}-R_s(f_{k,l},g_{k,l}))\frac{\partial R_s}{\partial g} = 0 \\ {\rm where}\ \\ \bar{f}_{k,l} = \frac{1}{4}(f_{k+1,l}+f_{k-1,l}+f_{k,l+1}+f_{k,l-1}) \\ \bar{g}_{k,l} = \frac{1}{4}(g_{k+1,l}+g_{k-1,l}+g_{k,l+1}+g_{k,l-1})
◦
디테일을 알 필요는 없음…
•
이를 이용해 다음과 같이 update rule 을 세울 수 있음.
fk,l(n+1)=fˉk,l(n)+λ(Ik,l−Rs(fk,l(n),gk,l(n)))∂Rs∂fgk,l(n+1)=gˉk,l(n)+λ(Ik,l−Rs(fk,l(n),gk,l(n)))∂Rs∂gf_{k,l}^{(n+1)} = \bar{f}_{k,l}^{(n)} + \lambda(I_{k,l} - R_s(f_{k,l}^{(n)},g_{k,l}^{(n)}))\frac{\partial R_s}{\partial f} \\ g_{k,l}^{(n+1)} = \bar{g}_{k,l}^{(n)} + \lambda(I_{k,l} - R_s(f_{k,l}^{(n)},g_{k,l}^{(n)}))\frac{\partial R_s}{\partial g}
◦
Boundary 부분에서의 (f,g)(f,g) 는 앞선 Occluding Boundary 세션에서 이미 구해놓은 값을 사용함.
◦
나머지 (f,g)(f,g) 는 (0,0)(0,0) 으로 initialize 한 뒤에 update 할 수 있음.

Shape from Surface Normals

•
Surface Normal 로 부터 3D Shape 을 만드는 과정은 3D Shape 를 Surface Normal 로 만드는 과정의 반대과정임.
•
3D Shape 를 Surface Normal 로 만들기 위해서는 depthmap 을 differentiate 해야하므로 반대과정은 intergration 을 하면 됨.
z(x,y)=z(x0,y0)+∫(x0,y0)x,y−(pdx+qdy)z(x,y) = z(x_0,y_0) + \int_{(x_0,y_0)}^{x,y} -(pdx + qdy)
◦
(x0,y0)(x_0,y_0) 부터 (x,y)(x,y) 까지 갈 수 있는 임의의 경로로 intergration 을 하면 됨. (가능한 경로를 모두 찾아 값을 구하고 average 해도 됨.)
◦
더 좋은 방법은 (p,q)=(−∂z∂x,−∂z∂y)(p,q) = (-\frac{\partial z}{\partial x}, -\frac{\partial z}{\partial y}) 가 성립해야 하므로 반대로, 이것이 성립하도록 optimization problem 을 설계하고 풀 수 있음.
E(z)=∫∫(∂z∂x+p)2+(∂z∂y+q)2dxdyE(z) = \int\int (\frac{\partial z}{\partial x} + p)^2 + (\frac{\partial z}{\partial y}+q)^2dxdy
◦
위 식은 Fast Fourier Transform 으로 효과적으로 풀 수 있다고 함. (디테일은 다루지 않음.)