Duplicate

Lecture 19 | Optical Flow

수강 일자
2022/11/08

Optical Flow

•
Apparent motion of brightness patterns
◦
실제 움직임이 아닌, 이미지 상에서 물체가 어떻게 움직였는가
◦
각 픽셀의 움직임을 오직 시각적인 관점에서 계산하는 과정
◦
“이상적”으로 Optical Flow 는 3차원 velocity vector 를 이미지 상으로 projection 한 것임.
•
Time-varying image (video) 에서 scene object 의 움직임을 찾는 과정이 Optical Flow
◦
Motion 은 segmentation 에 있어서도 중요한 정보로 활용됨. (동일한 물체는 동일한 motion 을 취할 가능성이 높기 때문임)
•
동영상 분석에서 필수적인 요소
◦
Track object behavior
◦
Correct for camera jitter (stabiliazation)
◦
Align images (mosaics): 동영상으로부터 mosaic 를 생성하는데 Optical Flow 를 활용
◦
동영상 형태로 multiview 를 얻고 이로부터 3D reconstruction 을 할 때 사용

Optical Flow Examples

•
Tracking - Rigid Objects
◦
시간에 따라 보이는 형태가 크게 달라지지 않는 강체에 대한 tracking
•
Tracking - Non-rigid Objects
◦
관절 등 보이는 형태가 달라지는 시간에 따라 달라지는 물체에 대한 tracking
•
Face Tracking
◦
Landmark Point 를 이용해 mesh 형태로 얼굴 mask 를 만들고 tracking
•
Behavior Analysis
◦
Query 와 비슷한 행동을 하는 사람을 tracking
◦
거동이 수상한 사람을 찾는다던지, 병원에서 낙상을 한다던지하는 것을 detect 하는데 사용함.

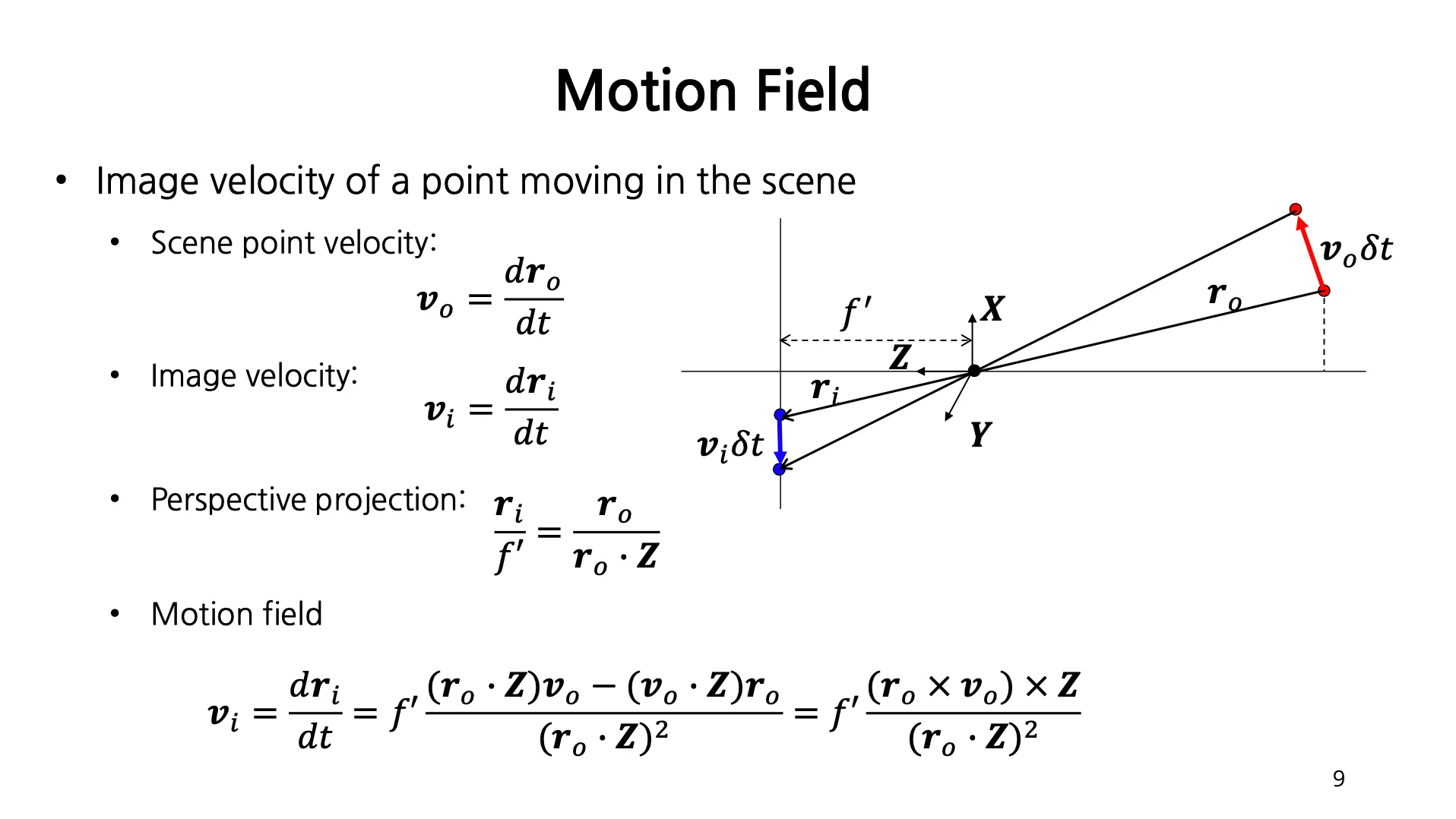
Motion Field

•
Scene 에서 움직이는 점에 대한 Scene Point Velocity 를 다음과 같이 정의함.
◦
ror_o 는 camera center 로부터 특정 점까지의 거리 벡터
vo=drodtv_o = \frac{dr_o}{dt}
•
Scene 에서 움직이는 점에 대한 Image Velocity 는 다음과 같이 정의됨.
◦
rir_i 는 camera center 로부터 Image Plane 상의 상 까지의 거리 벡터
vi=dridtv_i = \frac{dr_i}{dt}
•
Perspective Projection 을 통한 관계는 다음과 같음.
rif′=roro⋅Z\frac{r_i}{f'} = \frac{r_o}{r_o\cdot Z}
•
앞선 Perspective Projection 관계를 통해 viv_i 를 계산하면 다음과 같음.
◦
ror_o 위치에서 vov_o 의 속도로 움직이는 물체가 Image Plane 상에서는 어떤 속도로 움직이는가
vi=dridt=f′(ro⋅Z)vo−(vo⋅Z)ro(ro⋅Z)2=f′(ro×vo)×Z(ro⋅Z)2v_i = \frac{dr_i}{dt} = f' \frac{(r_o \cdot Z)v_o - (v_o\cdot Z)r_o}{(r_o \cdot Z)^2} = f'\frac{(r_o \times v_o)\times Z}{(r_o \cdot Z)^2}

Optical Flow

•
Motion Field 와는 달리 3차원 상에서 물체 및 점의 이동속도는 알지 못한 채, 연속적인 이미지만 가지고 동일한 픽셀이 어떻게 움직였는지만 봄.
◦
Optical Flow 는 순수하게 시각정보만을 이용해서 계산한 movement 임.

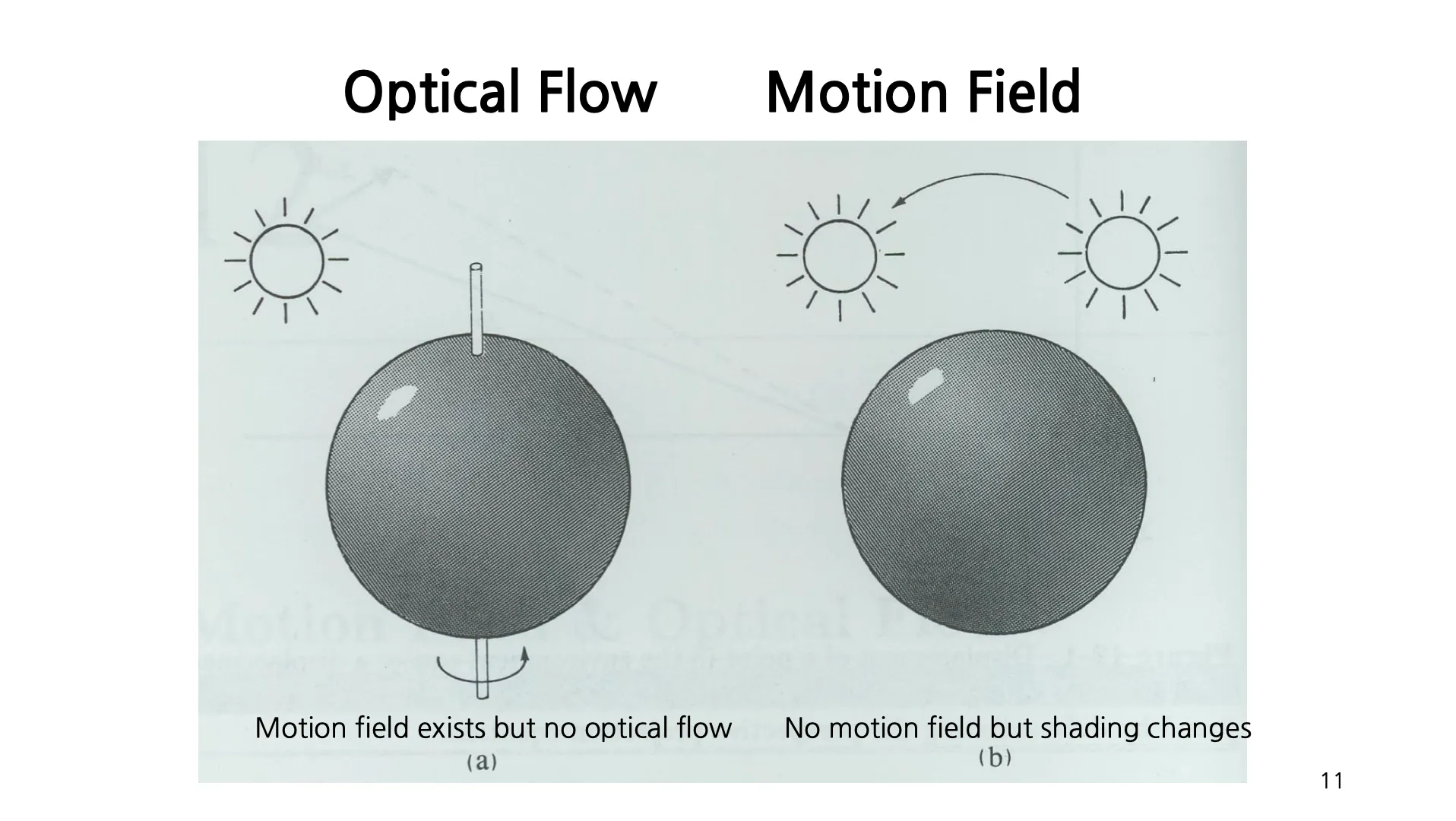
Optical Flow ≠\neq Motion Field

•
좌측은 당구공을 돌린 상황
◦
Motion Field 는 존재 (속도가 존재하므로) 하나 Optical Flow 는 없음 (보이는 것의 차이 X)
•
우축은 광원을 움직인 상황
◦
Motion Field 는 존재하지 않으나 (속도가 0) Optical Flow 는 존재함 (보이는 것의 차이 O)

Three Optical Flow Assumptions

1.
Brightness Consistency
•
동일한 영역은 다음 이미지에서도 동일하게 측정된다는 (ex. Image Brightness) 가정
2.
Spatial Coherence
•
이미지 상에서의 neighborhood point 는 공간 상에서도 neighborhood 이며 같은 surface 위에 존재하고 비슷한 motion 을 가진다는 가정
3.
Temporal Persistence
•
(Video 기반일 경우) 인접한 frame 사이의 시간 간격은 매우 작다는 가정 → 크게 움직이지 않음.

Problem Definition: Optical Flow

•
두 장의 이미지 H(x,y)H(x,y) 와 I(x,y)I(x,y) 가 주어지고 시간 간격이 짧다고 가정함.
•
Key Assumptions
◦
Color Constancy: Brightness Consistency 의 color 버전의 가정
◦
Small Motion: 두 점 사이의 거리가 멀지 않다는 가정
•
Optical Flow Constraint Equation
◦
tt 시각에서 (x,y)(x,y) 의 위치에 있던 점이 t+δtt + \delta t 시각에서 (x+uδt,y+vδt)(x+u\delta t, y+v\delta t) 라고 가정함.
◦
첫 번째 가정에 의해 다음이 성립함.
I(x+uδt,y+vδt,t+δt)=I(x,y,t)I(x+u\delta t, y + v\delta t, t+\delta t) = I (x,y,t)
◦
두 번째 가정에 의해 식이 다음과 같이 변경됨. (Taylor expansion of LHS up to first order)
I(x,y,t)+δx∂I∂x+δy∂I∂y+δt∂I∂t=I(x,y,t)I(x,y,t) + \delta x\frac{\partial I}{\partial x} + \delta y\frac{\partial I}{\partial y} + \delta t\frac{\partial I}{\partial t} = I(x,y,t)
◦
결국 다음과 같은 식이 성립하게 됨.
δx∂I∂x+δy∂I∂y+δt∂I∂t=0\delta x\frac{\partial I}{\partial x} + \delta y\frac{\partial I}{\partial y} + \delta t\frac{\partial I}{\partial t} = 0
◦
좌 우변을 δt\delta t 로 나누고 δt→0\delta t \rarr 0 으로 보내면 Optical Flow Constraint Equation 을 얻음.
Ixu+Iyv+It=0I_x u + I_y v + I_t = 0
▪
u=dxdtu = \frac{dx}{dt}, v=dydtv = \frac{dy}{dt}
▪
위 식은 uvuv space 에서 직선으로 표현됨.
▪
IxI_x, IyI_y 는 intensity 가 xx, yy 방향으로 얼마나 바뀌었는가를 의미함.
▪
ItI_t 는 intensity 가 시간에 따라서 얼마나 바뀌었는가를 의미함.
▪
직선으로 표현은 되지만 정확한 uu, vv 값을 구할 수는 없음.

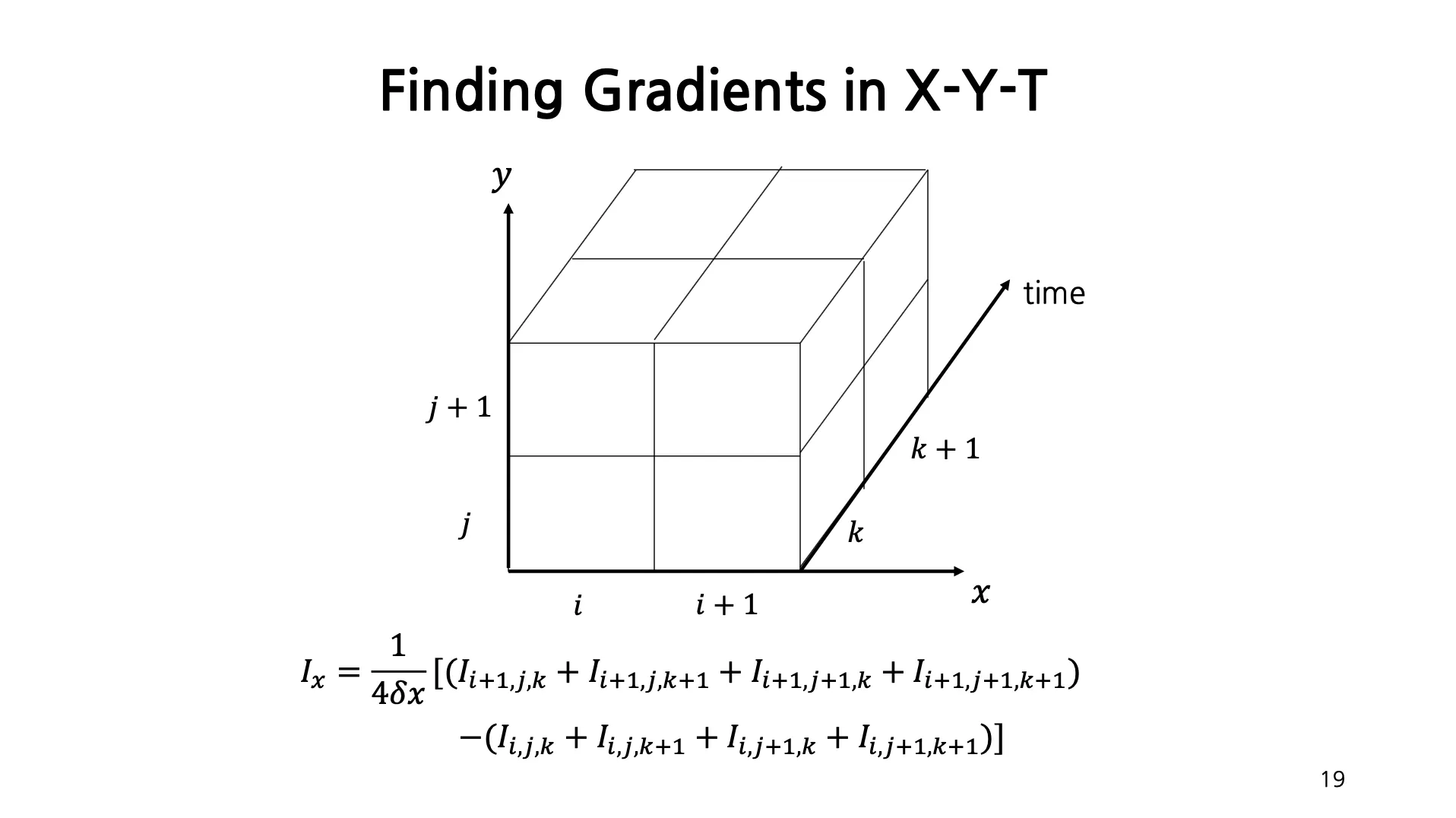
Finding Gradients in X-Y-T

•
Discrete 한 경우에서 IxI_x 를 구하는 방법 중 하나임.
•
xx 가 큰 4개의 항목에서 xx 가 작은 4개의 항목을 빼고 4δx4\delta x 로 나눠줌.

Example

•
(3,3)(3,3) 점에 대해 Optical Flow Constraint Equation 을 적용하면 v=1v=1 이라는 식이 됨.
•
하지만 uu 에 대한 정보는 얻을 수 없음.

Barber Pole Illusion

•
실제 원통은 zz 축을 기준으로 돌고 있지만, 위로 올라가는 것처럼 보임.
•
Motion Field 는 도는 방향이지만, Optical Flow 는 위 방향임.

Aperture Problem

•
전체 영역을 보면 어느 방향으로 움직이는지 알 수 있지만, 작은 Aperture 영역만을 보면 어느 방향으로 움직이는지 확실하지 않음. (Motion direction in a small aperture is ambiguous)
•
패턴의 선과 평행한 motion component 는 visual input 으로부터 추론될 수 없음.
•
패턴의 선과 수직인 motion component 만 visual input 으로부터 추론할 수 있음.

Multiple Constraint

•
한 점으로 인해서 구하는 직선 만으로는 uu, vv 를 결정할 수 없음.
•
여러 점들 각각에 대해서 Optical Flow Constraint 를 적용하고 얻은 직선들이 만나는 점이 실제 uu, vv 로 볼 수 있음.

Area-based Method

•
하나의 pixel 이 아닌, window 내부의 여러 pixel 하나하나에 대해서 uvuv space 상의 직선을 얻을 수 있고, 가장 교점이 많은 점이 실제 patch 가 움직이는 uu, vv 임을 알 수 있음.
∑x,y(Ixu+Iyv+It)2=0\sum_{x,y} (I_xu+I_yv +I_t)^2 = 0
◦
Spatial Smoothness 가정을 활용하면 window 내부의 점들을 같은 object 의 같은 surface 일 가능성이 있고 motion 이 다를 수는 있지만 연속적이고 비슷하다고 볼 수 있음.
•
Practical 한 경우 다음과 같이 minimization problem 으로 볼 수 있음. (Lucas-Kanade Method)
min⁡u,vE(u,v)=∑x,y(Ixu+Iyv+It)2\min_{u,v} E(u,v) = \sum_{x,y} (I_xu+I_yv +I_t)^2
◦
최소 지점을 구하기 위해 uu, vv 에 대한 미분을 생각해 볼 수 있음.
◦
RR 은 xx, yy 로 만드는 region
∂E∂u=∑R(Ixu+Iyv+It)Ix=0∂E∂v=∑R(Ixu+Iyv+It)Iy=0\frac{\partial E}{\partial u} = \sum_R (I_xu+I_yv +I_t)I_x = 0 \\ \frac{\partial E}{\partial v} = \sum_R (I_xu+I_yv +I_t)I_y = 0
◦
uu, vv 만 남기고 우측으로 넘기면 다음과 같은 식을 얻을 수 있음.
[∑RIx2]u+[∑RIxIy]v=−∑RIxIt[\sum_R I_x^2]u +[\sum_R I_xI_y]v = -\sum_R I_xI_t \\
[∑RIxIy]u+[∑RIy2]v=−∑RIyIt[\sum_R I_xI_y]u +[\sum_R I_y^2]v = -\sum_R I_yI_t \\
◦
이는 matrix form 으로 다음과 같이 변형됨.
[∑Ix2∑IxIy∑IxIy∑Iy2][uv]=[−∑IxIt−∑IyIt]\begin{bmatrix} \sum I_x^2 & \sum I_xI_y \\ \sum I_xI_y & \sum I_y^2 \\ \end{bmatrix} \begin{bmatrix} u \\ v \\ \end{bmatrix} = \begin{bmatrix} -\sum I_xI_t \\ -\sum I_yI_t \\ \end{bmatrix}
▪
2×22\times2 matrix 의 역행렬을 쉽게 구할 수 있기 때문에 이를 양변의 좌측에 곱하면 최종적으로 uu, vv 를 구할 수 있음.

Low Texture Region - Bad

•
매우 uniform 한 영역이기 때문에 gradient 값이 작음.
•
정확한 Optical Flow 값을 계산하는 것은 쉽지 않음.

Edges - So So

•
Edge 방향으로는 구하기 어렵지만, 수직인 방향으로는 Optical Flow 를 계산할 수 있음.

High Textured Region - Good

•
다양한 방향으로의 edge 정보가 있기 때문에 Optical Flow 를 쉽게 계산할 수 있음.
•
어떤 픽셀은 Optical Flow 를 구하기 쉽고 어떤 픽셀은 구하기 어려움.

Revisiting the Small Motion Assumption

•
달리는 차에서 동영상을 찍으면 이미지간 시간 간격이 좁더라도, 자동차의 속도가 빠르기 때문에 이미지 간 displacement 가 생각보다 클 수 있음.
•
Small Motion Assumption 을 적용할 수 없기 때문에 (First Order Taylor Approximation 을 적용하는데 무리가 있음.) 기존 Optical Flow 를 적용하기 어려움.
•
이 경우, resolution 을 낮추어서 movement 의 displacement 를 줄여버리는 방법이 있음.

Coarse-to-fine Optical Flow Estimation

•
Gaussian Pyramid 를 만든 뒤, 가장 높은 레벨 (작은 resolution) 에서 displacement 가 1.25 pixel 이라면 Small Motion Assumption 을 적용할 수 있음.
•
Iterate 하게 Optical Flow 를 적용하여 uu, vv 를 구하고 upsampling 하는것을 반복함을 통해서 최종적인 값을 구해낼 수 있음.