Duplicate

CV_HW1

마감일
2022/10/03
제출자
전기정보공학부 2017-12433 김현우

1. Filters

In class, we have discussed the usage of two different filters, i.e., Gaussian filter and Median filter.
1.
[5] Describe the similarity of two filters in one sentence. Gaussian filter and Median filter both blurs (and can be used for denoising) the target image since they replace the original pixel value to weighted sum or median sampling the local region’s (itself + neighbors) pixel values.
2.
[5] Describe one key difference of two filters in one sentence. Gaussian filter consists of sampled 2D gaussian distribution and can be applied by direct convolution operation, but Median filter cannot since it just replaces the pixel with median value of neighbors inside the filter.
3.
[4] Assume we have an image with drastic change in magnitude as below (i.e., checkerboard). Which one of the two filters would preserve the boundaries of black boxes better? In other words, which one would make the output less blurry?
Median filter would make the output less blurry than Gaussian filter.
4.
[6] Describe the reason in one sentence. If we assume general small sized (odd-length) filter, unlike Gaussian filters that will show gray values (seems to be blurry) at the boundary between black and white region, Median filters will produce exact white values when applied to white pixels and black values when applied to black pixels which maintains existing patterns in all region.

2. Cross-correlation

Assume we have three image patches whose shapes are identical, i.e., f,g1,g2∈Rm×nf,g_1,g_2 \in \mathbb{R}^{m\times n}, where g1(i,j)=f(m−i,n−j)g_1(i,j)=f(m-i,n-j) and g2(i,j)=2×f(m−i,n−j)g_2(i,j)=2\times f(m-i,n-j) for all i,ji,j.
1.
[8] Calculate cross-corrleation of the patches Rfg1R_{f_{g_1}}, Rfg2R_{f_{g_2}}. The cross-correlation is derived by maximizing the similarity of the overlapped region of two images. To find the most similar region of two images f,g1f,g_1, generally we can find i,ji,j which minimizes below.
E(i,j)=∑k=ik=i+m∑l=jl=j+n[f(k,l)−g1(k−i,l−j)]2=∑k=ik=i+m∑l=jl=j+nf(k,l)2+g1(k−i,l−j)2−2f(k,l)g1(k−i,l−j)\begin{align*} E(i,j)&=\sum_{k=i}^{k=i+m}\sum_{l=j}^{l=j+n}[f(k,l)-g_1(k-i,l-j)]^2\\ &=\sum_{k=i}^{k=i+m}\sum_{l=j}^{l=j+n} f(k,l)^2+g_1(k-i,l-j)^2-2f(k,l)g_1(k-i,l-j) \end{align*}
Roughly we can maximize ∑k=i+1k=i+m∑l=j+1l=j+nf(k,l)g1(k−i,l−j)\sum_{k=i+1}^{k=i+m}\sum_{l=j+1}^{l=j+n} f(k,l)g_1(k-i,l-j) to find the target i,ji,j and we call this as the cross-correlation of image ff on template g1g_1.
However, all of the images have the same size of m×nm\times n, the sliding region out of the range (ouside the image) should be modified as below.
Rfg1(i,j)=∑k=ik=m∑l=jl=nf(k,l)g1(k−i,l−j)=∑k=ik=m∑l=jl=nf(k,l)f(m−k+i,n−l+j)\begin{align*} R_{f_{g_1}}(i,j)&=\sum_{k=i}^{k=m}\sum_{l=j}^{l=n} f(k,l)g_1(k-i,l-j) \\ &=\sum_{k=i}^{k=m}\sum_{l=j}^{l=n} f(k,l)f(m-k+i,n-l+j) \end{align*}
This can be seen that it is the same as the result of convolution with itself using zero-padding.
In same sense, we can find the cross correlation of image ff on template g2g_2 as below.|
Rfg2(i,j)=∑k=ik=m∑l=jl=nf(k,l)g2(k−i,l−j)=∑k=ik=m∑l=jl=n2f(k,l)f(m−k+i,n−l+j)\begin{align*} R_{f_{g_2}}(i,j)&=\sum_{k=i}^{k=m}\sum_{l=j}^{l=n} f(k,l)g_2(k-i,l-j) \\ &=\sum_{k=i}^{k=m}\sum_{l=j}^{l=n} 2f(k,l)f(m-k+i,n-l+j) \end{align*}
Also this can be seen that it is twice the result of convolution with itself using zero-padding.
2.
[8] Calculate normalized cross-correlation Nfg1N_{f_{g_1}}, Nfg2N_{f_{g_2}}. Since the cross-correlation can give unwanted result if there exists the region which gives higher value of product sum of two image than exact matching region, we can apply noramlization on the given cross-correlation to handle this problem.
Nfg1=∑k=ik=m∑l=jl=nf(k,l)f(m−k+i,n−l+j)[∑k=ik=m∑l=jl=nf(k,l)2]1/2[∑k=ik=m∑l=jl=nf(m−k+i,n−l+j)2]1/2=∑k=ik=m∑l=jl=nf(k,l)f(m−k+i,n−l+j)2[∑k=ik=m∑l=jl=nf(k,l)2]1/2\begin{align*} N_{f_{g_1}}&=\frac{\sum_{k=i}^{k=m}\sum_{l=j}^{l=n} f(k,l)f(m-k+i,n-l+j)}{[\sum_{k=i}^{k=m}\sum_{l=j}^{l=n} f(k,l)^2]^{1/2}[\sum_{k=i}^{k=m}\sum_{l=j}^{l=n} f(m-k+i,n-l+j) ^2]^{1/2}} \\ \\ &= \frac{\sum_{k=i}^{k=m}\sum_{l=j}^{l=n} f(k,l)f(m-k+i,n-l+j)}{2[\sum_{k=i}^{k=m}\sum_{l=j}^{l=n} f(k,l)^2]^{1/2}} \end{align*}
We used [∑k=ik=m∑l=jl=nf(k,l)2]1/2=[∑k=ik=m∑l=jl=nf(m−k+i,n−l+j)2]1/2[\sum_{k=i}^{k=m}\sum_{l=j}^{l=n} f(k,l)^2]^{1/2} = [\sum_{k=i}^{k=m}\sum_{l=j}^{l=n} f(m-k+i,n-l+j) ^2]^{1/2} to simplify the first row equation to be second row equation.
In the same way, we can calculate normalized cross-correlation of image ff on template g2g_2.
Nfg2=2∑k=ik=m∑l=jl=nf(k,l)f(m−k+i,n−l+j)[∑k=ik=m∑l=jl=nf(k,l)2]1/2[∑k=ik=m∑l=jl=n4f(m−k+i,n−l+j)2]1/2=2∑k=ik=m∑l=jl=nf(k,l)f(m−k+i,n−l+j)4[∑k=ik=m∑l=jl=nf(k,l)2]1/2=∑k=ik=m∑l=jl=nf(k,l)f(m−k+i,n−l+j)2[∑k=ik=m∑l=jl=nf(k,l)2]1/2\begin{align*} N_{f_{g_2}}&=\frac{2\sum_{k=i}^{k=m}\sum_{l=j}^{l=n} f(k,l)f(m-k+i,n-l+j)}{[\sum_{k=i}^{k=m}\sum_{l=j}^{l=n} f(k,l)^2]^{1/2}[\sum_{k=i}^{k=m}\sum_{l=j}^{l=n} 4f(m-k+i,n-l+j) ^2]^{1/2}} \\ \\ &= \frac{2\sum_{k=i}^{k=m}\sum_{l=j}^{l=n} f(k,l)f(m-k+i,n-l+j)}{4[\sum_{k=i}^{k=m}\sum_{l=j}^{l=n} f(k,l)^2]^{1/2}} \\ \\ &= \frac{\sum_{k=i}^{k=m}\sum_{l=j}^{l=n} f(k,l)f(m-k+i,n-l+j)}{2[\sum_{k=i}^{k=m}\sum_{l=j}^{l=n} f(k,l)^2]^{1/2}} \end{align*}
3.
[4] Compare the result of two different cross-correlations in one or two sentence. The original cross-correlation shows 2Rfg1=Rfg22R_{f_{g_1}} = R_{f_{g_2}}, but the normalized cross-correlation shows Nfg1=Nfg2N_{f_{g_1}} = N_{f_{g_2}}. The original cross-correlation will fail to find matching region which has pixel values of such as ×2\times 2, ×3\times3 of the original image region, but the normalized cross-correlation will not.
(Note: For question 2-1 and 2-2, you must show the derivation of your answer to get the full credit.)

3. Fourier Frequency Spectrum

For the outcome of Fourier Transform F(u,v)=R(u,v)+iI(u,v)F(u,v)=R(u,v)+iI(u,v):
1.
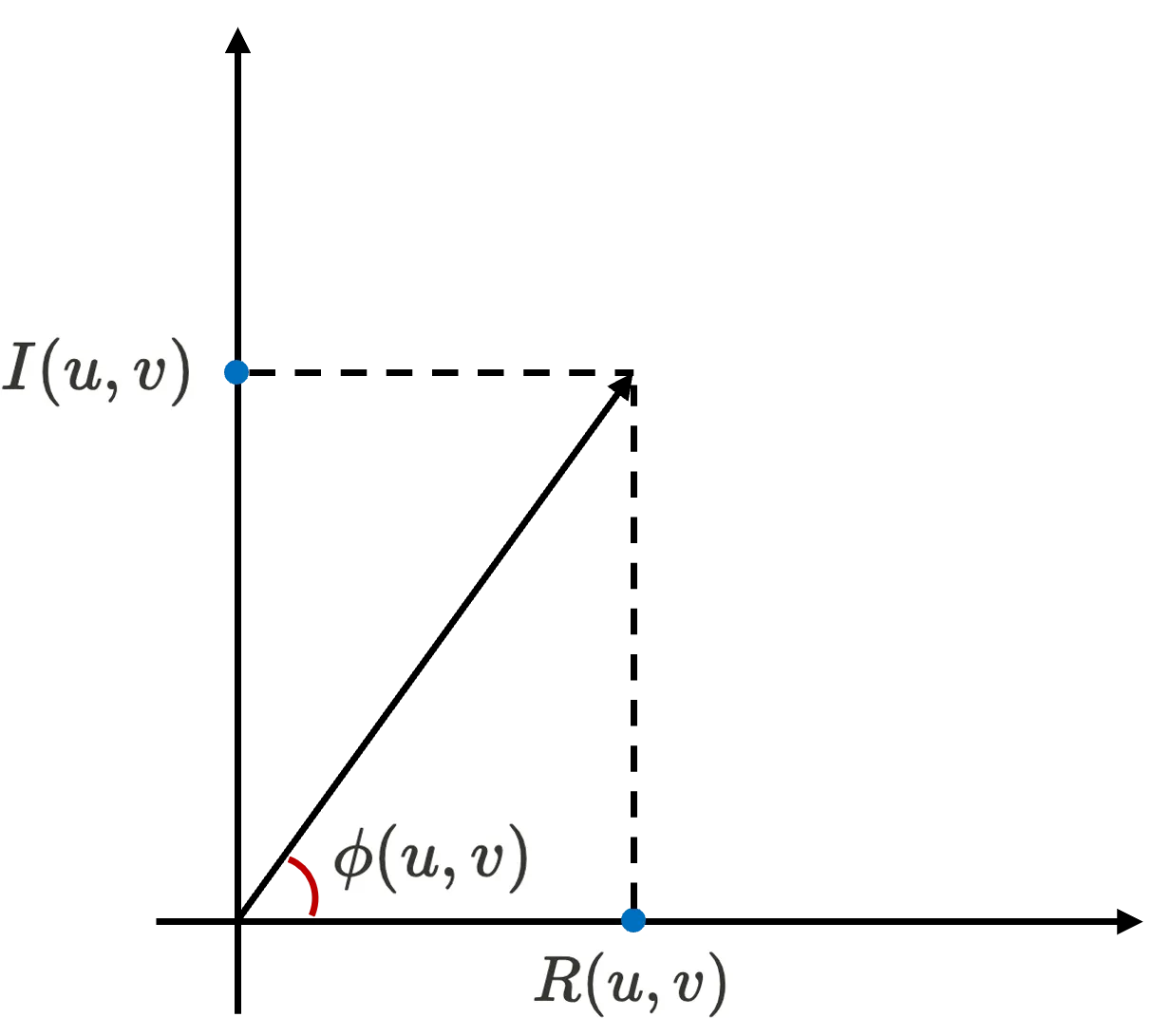
[5] Derive the phase spectrum ϕ(u,v)\phi(u,v). Below figure is the visualization of the output of Fourier transform in 2D coordinate system where xx-axis indicates real domian and yy-axis indicates imaginary domain with phase spectrum ϕ(u,v)\phi(u,v) indicated.
Since the phase spectrum indicates the angle of vector (R(u,v),I(u,v))(R(u,v),I(u,v)) with xx-axis as above, we can say the result as ϕ(u,v)=arctan⁡(I(u,v)R(u,v))\phi(u,v)=\arctan(\frac{I(u,v)}{R(u,v)}).
2.
[5] Derive the power spectrum P(u,v)P(u,v).
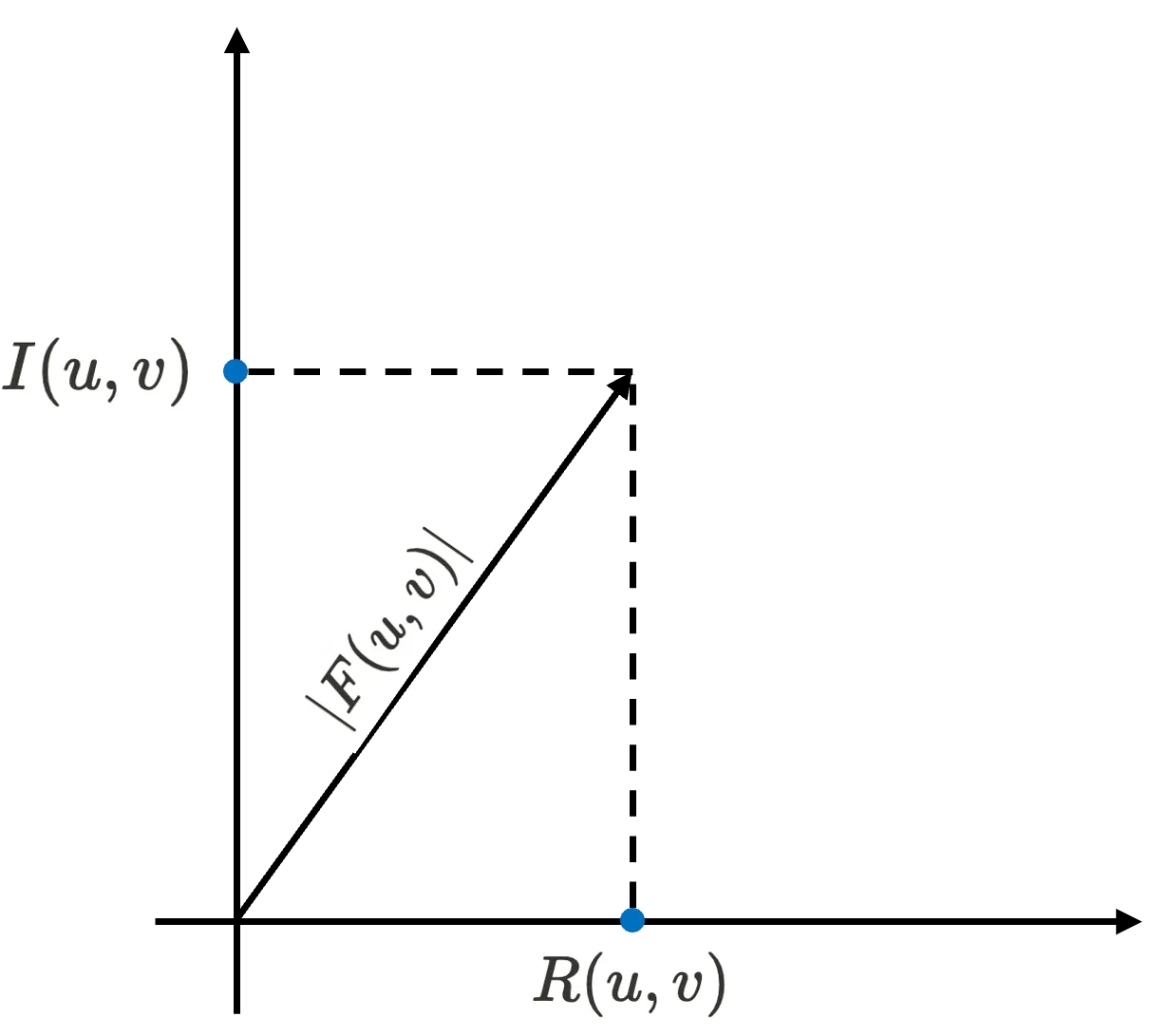
Below figure is the visualization of the output of Fourier transform in 2D coordinate system where xx-axis indicates real domian and yy-axis indicates imaginary domain with magnitude spectrum ∣F(u,v)∣|F(u,v)| indicated.
The magnitude spectrum of the F(u,v)F(u,v) is ∣F(u,v)∣=R(u,v)2+I(u,v)2|F(u,v)| = \sqrt{R(u,v)^2 +I(u,v)^2}. Since the power spectrum is the square of the magnitude spectrum, we can say the result as P(u,v)=R(u,v)2+I(u,v)2P(u,v) = R(u,v)^2 + I(u,v)^2.

4. Gaussian Pyramids

In this question, we are applying Gaussian pyramid to a 100×100100 \times 100 greyscale image (I0∈R100×100I_0 \in \mathbb{R}^{100\times 100}).
1.
[5] We would like to apply Gaussian smoothing first. If we use 5×55\times 5 2D Gaussian filter, how many multiplications are required to obtain blurred image I1∈R100×100I_1 \in \mathbb{R}^{100\times 100}? For each pixel in I0I_0, we can think of applying 5×55 \times 5 2D Gaussian filter on it. Since applying filter on a pixel needs sum of product of 5×55\times 5 neighborhood pixels, we need 25 times of multiplication on each pixel in original image I0I_0. Since we have 100×100100\times 100 pixels on I0I_0, we need total 25×100×10025 \times 100\times 100 times of multiplications which is 250,000250,000 times.
2.
[5] If we use two 1D Gaussian filters instead of one 2D Gaussian filter, how many multiplications are required to obtain I1I_1? Consider the case we applying vertical 1D Gaussian filter with size of 5×15\times 1. For each row of image I0,I_0, we can think of applying 5×15\times 1 1D Gaussian filter on it. Since applying filter on a row need sum of product of 5 neighborhood rows, we need 5 times of multiplication on each row in original Image I0I_0. Since we have 100100 rows on I0I_0, we need total 5×1005\times 100 times of multiplication which is 500500 times. Without loss of generality, we can think of applying horizontal 1D Gaussian filter with size of 1×51\times 5 similar as vertical case. Then, we can know this process also needs 500500 times of multiplications. Thus, we totally need 1,0001,000 times of multiplication in this case.
3.
[5] Can we replace a 2D filter with two 1D filters to compute the Laplacian of an image? Explain your answer in one sentence. Since we use Difference of Gaussian (DoG) to compute the Laplacian of an image (because the computation cost of direct Laplacian is expensive) and 2D Gaussian filter can be replaced to two 1D Gaussian filter (vertical, horizontal), we can replace a 2D filter with two 1D filters to compute the Laplacian of an image.
4.
[5] Is multi-resolution correlation more time-efficient than single-resolution correla- tion for template matching? Explain your answer in one sentence. Generally, using multi-resolution correlation techniques such as image pyramid can be used to find strong matches between small template and small image which allows to reduce iteratation for finding matches for high resolution images, ultimately reduce time for matching compared to using single-resolution correlation (more time efficient).
(Hint 1: If we apply 3×33\times3 2D Gaussian filter to an image J0∈R3×3J_0\in \mathbb{R}^{3\times 3}, the number of multiplications required to obtain J1∈R3×3J_1 \in \mathbb{R}^{3\times 3} is 81.)
(Hint 2: Think how we actually compute the Laplacian of an image.)
(Note: For question 4-1 and 4-2, assume zero-padding and count 0×k(k∈R)0\times k(k\in \mathbb{R}) as a valid multiplication. You must show the derivation of your answer to get the full credit.)