Duplicate

Lecture 6 | Filters and Edge Detection

형태
Computer Vision
수강 일자
2022/09/21

What is the Computer Vision?

•
기계가 사람의 시각을 모방하는 것
•
시각 → Recognition (인지) + Reconstruction (재구성)

Why Vision Important?

•
뇌로 전달되는 정보의 90% 는 시각 정보
•
2022 년에 82% 의 인터넷 트래픽은 온라인 비디오가 차지할 것
•
Robotics, AR/VR, Medical Applications, Autonomous Driving …

Why is Computer Vision Difficult?

•
Ambiguity
•
Variations (Illumination, Object Pose, Clutter, Occlusions, Intra-class appearance, viewpoint)
•
Scale
•
Occlusion
•
Context and Human Experience → Context 나 인간의 경험만으로 완벽하지 못한 판단이 나올 수 있음

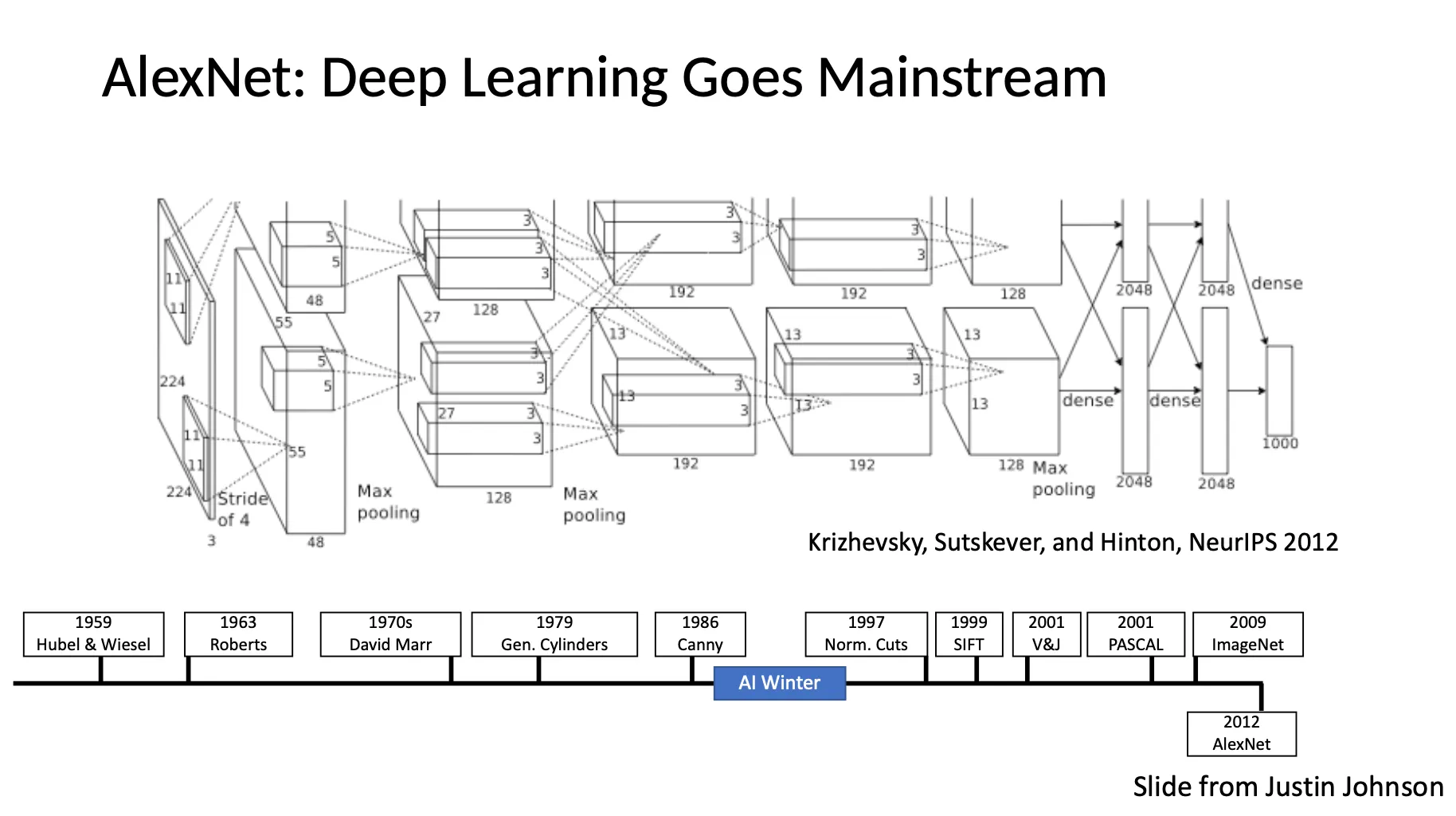
A Brief History of Computer Vision

•
Roberts (The Summer Vision Project) → David Marr (Stages of Visual Represenatation) → Recognition via Parts (1970s) → Recognition via Edge Detection (1980s) → Recognition via Grouping (1990s) → Recognition via Matching (2000s) → Face Detection → PASCAL Visual Object Challenge → ImageNet → AlexNet (Deep Learning)

What is the AI we are Talking Nowadays?

•
Traditional Programming 은 if-else 문으로 프로그램을 작성
•
Machine Learning based 방법론은 input 과 output 으로 프로그램 f(θ)f(\theta) 를 만들어냄
◦
Training data 를 잘 설명하는 θ\theta 를 찾아냄
•
f(θ)f(\theta) 는 과거에는 simpler models (ex. linear) 를 사용했지만, 최근에는 neural network 를 사용
◦
Large-Scale data 와 optimization 으로 최선의 parameter θ\theta 를 찾아냄
◦
알고리즘보다 데이터가 더 중요해졌음!
◦
Hand-design feature 를 뽑아낸 후에 사용할 수도, end-to-end 로 사용할 수도 있음

How To Represent an Image

•
RGB, 3 개의 채널 각각에 0∼280 \sim 2^8 까지의 값을 할당
•
I∈Rw×h×3I \in {\mathbb {R}}^{w\times h\times 3}

Image Filtering

•
Pixel-wise Filtering
◦
If=I+100I_f = I + 100 → Brighten
◦
If=I−100I_f = I-100 → Darken
◦
If=255−II_f = 255-I → Inversion
◦
If={If, if Ir>100 & ig<100 & Ib<1000,elseI_f = \begin{cases} I_f, \ {\rm if\ I_r > 100\ \&\ i_g <100\ \&\ I_b < 100} \\ 0, {\rm else} \end{cases} → Custom
•
Spatial Filtering
◦
픽셀 하나뿐만 아니라 각 픽셀의 주변을 같이 보면 더 흥미로운 feature 들을 뽑을 수 있음!
If(i,j)=∑k,l∈{−1,0,1}I(i+k,j+l)z(k,l)I_f(i,j)=\sum_{k,l \in \{-1,0,1\}} I(i+k,j+l)z(k,l)
▪
II: Image to filter over
▪
zz: Filter
▪
IfI_f: Filtered image
◦
z=[000010000]z = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{bmatrix}→ Identity filter
◦
z=[000100000]z = \begin{bmatrix} 0 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}→ Shifting right side 1 pixel
◦
z=19[111111111]z = \frac{1}{9} \begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{bmatrix}→ Moving average filter
◦
z=13[000111000]z = \frac{1}{3} \begin{bmatrix} 0 & 0 & 0 \\ 1 & 1 & 1 \\ 0 & 0 & 0 \end{bmatrix}→ Directional blur (Horizontal blurring)
◦
z=13[010010010]z = \frac{1}{3} \begin{bmatrix} 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \end{bmatrix}→ Direction blur (Vertical blurring)
◦
z(k,l)=12πσ2e−k2+l22σ2z(k,l)= \frac{1}{2\pi\sigma^2}e^{-\frac{k^2+l^2}{2\sigma^2}} → Gaussian blur
▪
σ\sigma 가 클수록 주변 픽셀의 영향이 커지면서 blurring 이 심해짐
◦
가운데가 +, 주변이 - 인 filter → Image sharpening
◦
z=13[−101−101−101]z = \frac{1}{3} \begin{bmatrix} -1 & 0 & 1 \\ -1 & 0 & 1 \\ -1 & 0 & 1 \end{bmatrix}→ Image differentiation (xx direction)
▪
Noise 에 굉장히 민감한 filter 이기 때문에 이를 이용해서 edge detection 을 할 경우 edge 가 아닌 부분도 edge 로 볼 수 있음!
◦
z=[−101−202−101]z = \begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{bmatrix}→ Image diffentiation (xx direction, sobel filter)
▪
Gaussian + Differentiation 이 합쳐진 filter 로, noise sensitivity 가 낮음!

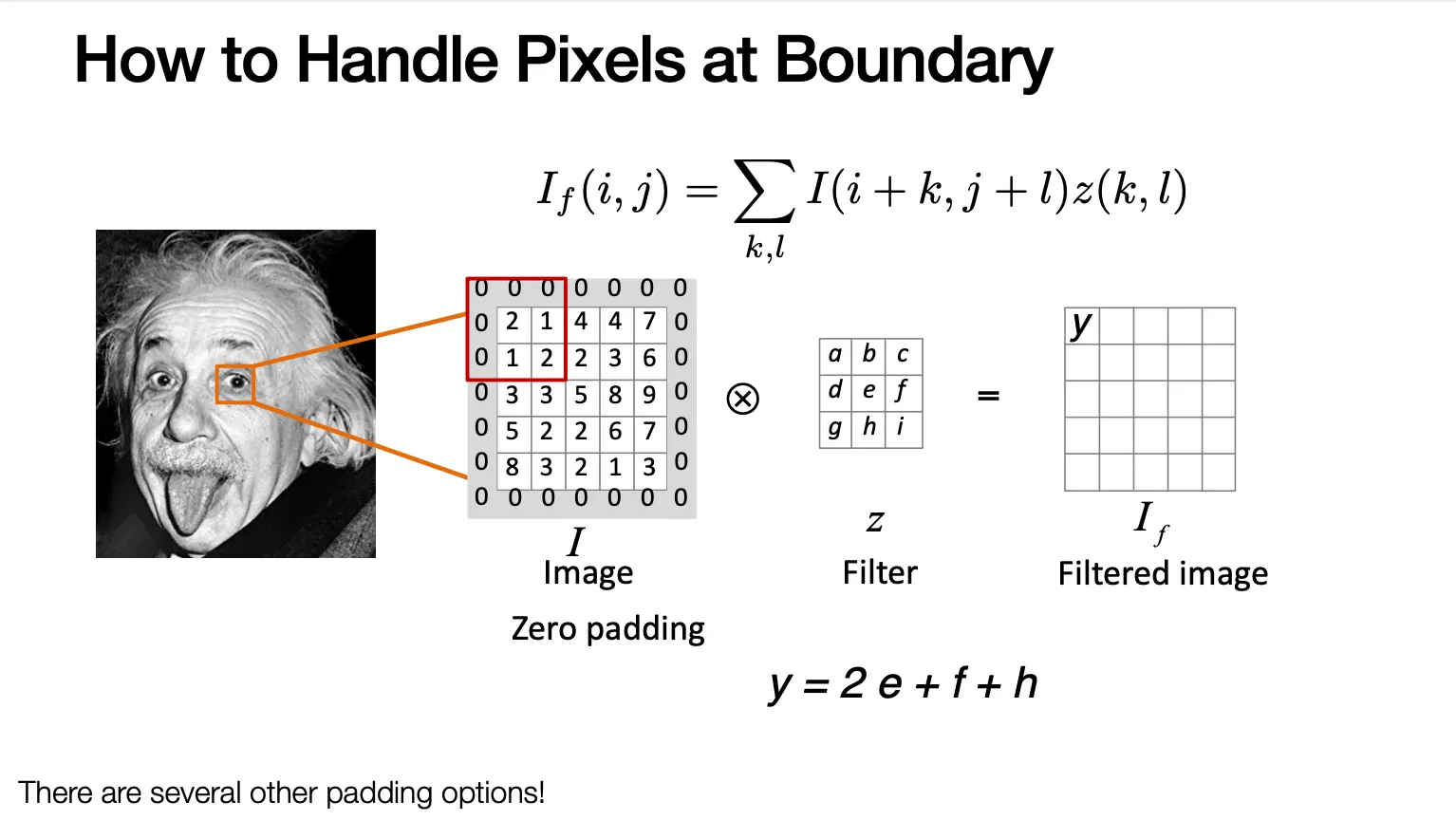
How to Handle Pixels at Boundary

•
이미지 바깥쪽에 0 을 두르는 zero-padding 을 하여 주변값을 채워넣음!

Correlation vs. Convolution

•
Image Correlation
I⊗z=IfIf(i,j)=∑k,lI(i+k,j+l)z(k,l)I \otimes z = I_f \\ I_f(i,j) = \sum_{k,l}I(i+k,j+l)z(k,l)
•
Image Convolution
I∗z=JJ(i,j)=∑k,lI(i−k,j−l)z(k,l)I *z = J \\ J(i,j) = \sum_{k,l}I(i-k,j-l)z(k,l)
◦
Filter 를 vertical, horizontal 하게 flip 하고 곱해서 더한다는 점이 Correlation 과 다름!

Properties of Convolutions

•
Shift Invariance: 이미지 내부의 위치에 상관없이 filter 내부의 값에만 영향을 받음
•
Commutative: f∗g=g∗ff*g=g*f
•
Associative: (f∗g)∗h=f∗(g∗h)(f*g)*h = f*(g*h)
•
Superposition, Distributes over Addition: h∗(f1+f2)=(h∗f1)+(h∗f2)h*(f_1+f_2) = (h*f_1) + (h*f_2)
•
Scalars factor out: kf∗g=f∗kg=k(f∗g)kf*g = f*kg = k(f*g)
•
Identity: f∗e=ff*e = f where e=[...,0,0,1,0,0,...]e=[..., 0,0,1,0,0,...] (unit impulse)
•
Associativity 때문에 linear filter 들을 하나씩 계속 겹쳐 넣은 것이 merge filter 를 넣은 것과 같게 되는 이점이 있음

Convolution as a Feature Extraction

•
사용하는 filter 에 따라서 response 가 달라지고, 이러한 response 를 feature 로 사용할 수 있음!
•
Filter Bank 는 scale, orientation, type 에 따라서 여러 filter 를 모아둔 것으로 다양한 feature 를 뽑을 수 있음
•
Convolutional Neural Network 에서는 optimal 한 filter 가 loss 를 최소화하는 방향으로 data 로부터 자동으로 최적화됨!

Image Gradient

•
Gradient 는 derivative 의 multivariate generalization
∇I=∂I(x,y)∂xi+∂I(x,y)∂yj\nabla I = \frac{\partial I(x,y)}{\partial x}i +\frac{\partial I(x,y)}{\partial y}j
•
Magnitude of gradient 는 contrast change (intensity, brightness change) 에 비례
∥∇I∥=(∂I∂x)2+(∂I∂y)2\|\nabla I \|=\sqrt{(\frac{\partial I}{\partial x})^2 + (\frac{\partial I}{\partial y})^2}
•
Direction of gradient 는 contrast change 가 가장 가파르게 일어나는 방향
tan⁡−1(∂I∂x/∂I∂y)\tan^{-1}(\frac{\partial I}{\partial x}/\frac{\partial I}{\partial y})

Edge Detection

•
이미지에서 edge 는 무엇인가?
◦
Depth discontinuity
◦
Illumination discontinuity
◦
Surface color discontinuity
•
가장 간단한 방법은 magnitude of gradient 를 thresholding 하는 것
∥∇I∥>ϵ\|\nabla I \| > \epsilon
◦
이러한 방법은 대게 non-locality (너무 굵은 edge 가 나오는 현상), discontinuity (edge 가 끊기는 현상) 가 나타남

Edge Localization: Non-maximum Suppresion

•
Non-locality 의 해결방안
•
Threshold 를 넘어 edge 로 선언된 각 픽셀별로, 해당 픽셀이 가진 gradient direction 의 양쪽 방향으로 이동하여 찾은 두 개의 neighbor pixel 과 gradient magnitude 를 비교하여 본인이 가장 높은 값을 가지지 않으면 해당 픽셀은 edge 에서 박탈함

Edge Linking

•
Discontinuity 의 해결방안
•
Weak edge 로 선언된 픽셀에서 tangent direction 으로 이동하여 발견한 픽셀이 weak edge 면 한 번 더 반복하고, strong edge 이면 해당 edge 와 연결, 그 둘이 아니면 reject 함.

Edge Prediction: Hysteresis

•
두 개의 threshold 를 두어 high threshold 보다 큰 픽셀은 바로 strong edge 로, low threshold 보다 작은 픽셀은 바로 reject 함
•
두 threshold 사이의 픽셀들은 weak edge 로 선언하고 strong edge 와 연결된 픽셀들만 최종 edge 로 선택함

Is Edge Detector Solved?

•
Canny edge detector 가 좋은 성능을 보이고 있지만, 많은 경우에 semantic 한 물체에 기반한 edge 를 그려내지는 못함 → 이 분야의 연구들이 이루어지고 있음
•
ex. Semantic Edge Detection with Diverse Deep Supervision