Duplicate

Lecture 7 | Camera Model

수강 일자
2023/02/26

Overview: Camera Projections

•
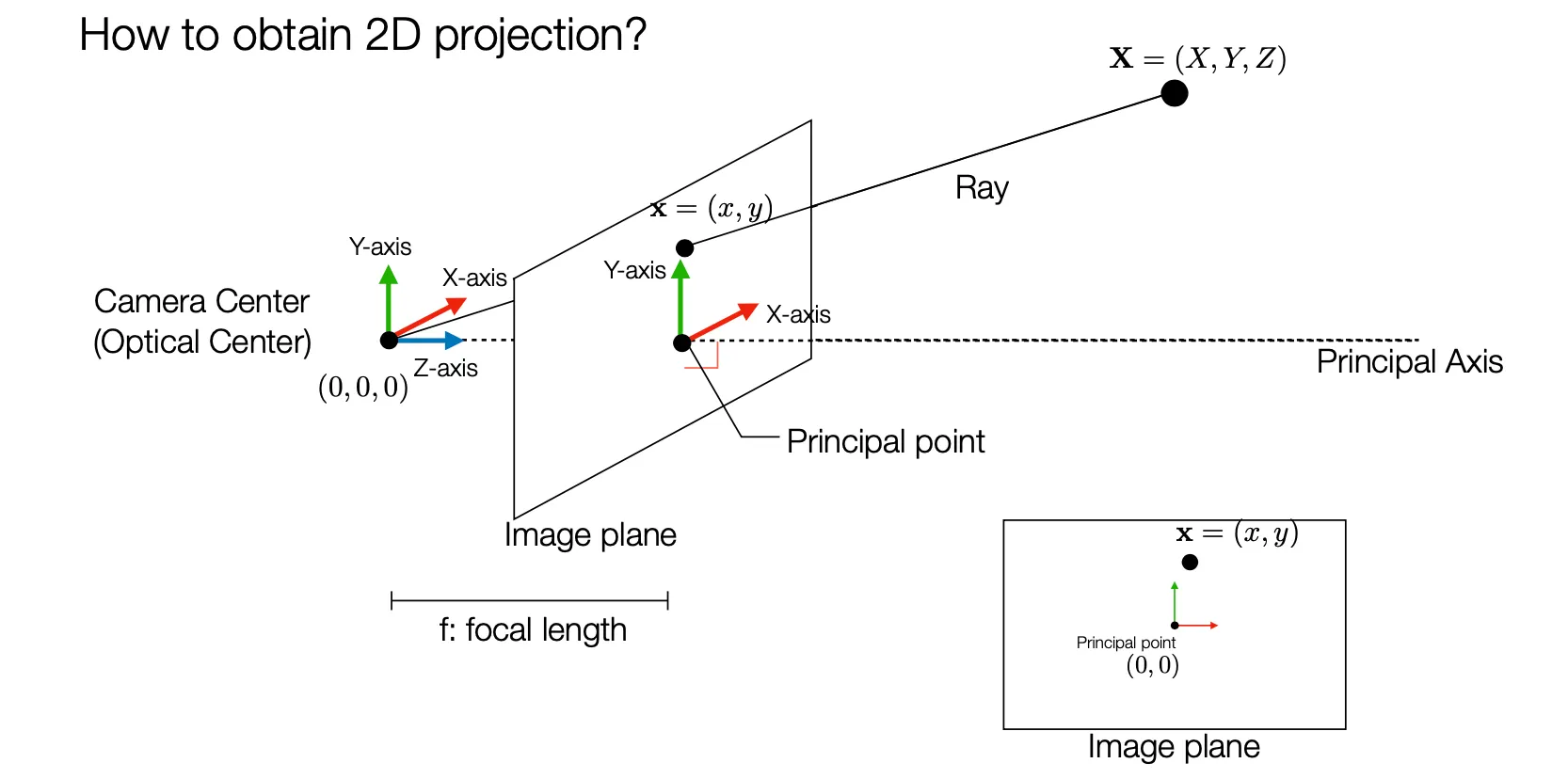
일반적으로 상은 Camera Center (Pinhole) 뒤 쪽에 focal length ff 만큼 거리의 위치에 생기지만, 편의를 위해서 Camera Center 앞 쪽 ff 만큼 거리에 그리는 경우가 많음.
•
Image Plane 과 수직인 axis 를 Principle Axis 로, 그 교점을 Principle Point 라고 부름.
•
Camera Center 와 물체의 특정 위치를 잇는 선을 3D Ray 라고 하고 이는 Image Plane 에서 상으로 맺힘.
◦
같은 3D Ray 위에 있는 점은 Image Plane 에서 같은 위치에 상으로 맺힘.
•
2D Image Plane 위의 점 x=(x,y){\rm x} = (x,y) 가 3D Point X=(X,Y,Z){\rm X} = (X,Y,Z) 와 대응된다면, 다음이 성립함.
f:y=Z:Y→y=fYZf:x=Z:X→x=fXZ(X,Y.Z)T→(fXZ,fYZ)=(fX,fY,Z)f:y = Z:Y \to y = f\frac{Y}{Z} \\ f:x = Z:X \to x = f\frac{X}{Z} \\ \quad \\ (X,Y.Z)^T \to (f\frac{X}{Z}, f\frac{Y}{Z}) = (fX,fY,Z)
◦
3D coordinates 에 scalar kk 가 곱해지더라도 동일한 2D Plane 상의 점에 대응됨을 알 수 있음.

Camera Intrinsic Parameters

(XYZ1)→(fXfYZ)=[f0f010](XYZ1)\begin{pmatrix} X \\ Y \\ Z \\ 1 \\ \end{pmatrix} \to \begin{pmatrix} fX \\ fY \\ Z \\ \end{pmatrix} = \begin{bmatrix} f & & & 0 \\ & f & & 0\\ & & 1 & 0 \\ \end{bmatrix} \begin{pmatrix} X \\ Y \\ Z \\ 1 \\ \end{pmatrix}
•
3D Point 를 Homogeneous Coordinate 로 나타낸 것을 2D Point 를 Homogeneous Coordinate 로 나타낸 것으로 변환하기 위해서 위와 같이 focal length ff 를 기반으로 3×43\times4 matrix 를 구성할 수 있음.
•
위 3×43\times4 matrix 는 다음과 같이 표현할 수 있음.
[f0f010]=[ff1][101010]=K[I∣0]\begin{bmatrix} f & & & 0 \\ & f & & 0\\ & & 1 & 0 \\ \end{bmatrix} = \begin{bmatrix} f & & \\ & f & \\ & & 1 \\ \end{bmatrix} \begin{bmatrix} 1 & & & 0 \\ & 1 & & 0\\ & & 1 &0 \\ \end{bmatrix} = K[{{\rm{I}}}| 0]
◦
이 분리된 matrix 의 앞을 Intrinsic Parameter (K)(K), 뒤를 Extrinsic Parameter ([I∣O])([I|O])라고 부름.
•
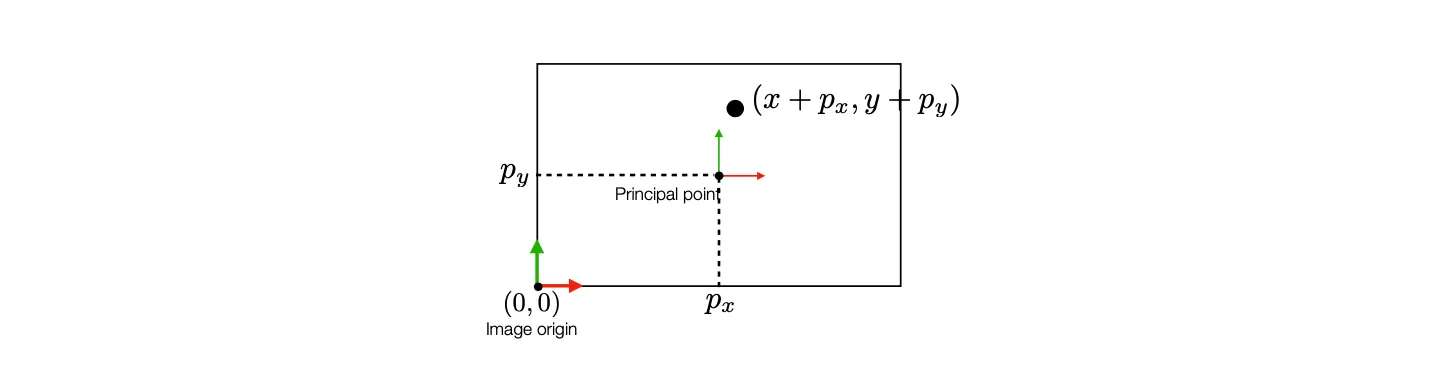
일반적으로 Image Plane 위의 origin 은 중심점이 아니라, 좌 하단의 점 등 corner point 이기 마련임. 이에 대한 보정은 다음과 같이 할 수 있음.
(X,Y,Z)T→(fXZ+px,fYZ+py)(XYZ1)→(fX+ZpxfY+ZpyZ)=[fpx0fpy010](XYZ1)=[fpxfpy1][101010](XYZ1)(X,Y,Z)^T \to (f\frac{X}{Z} + p_x, f\frac{Y}{Z}+p_y) \\ \begin{align*} \begin{pmatrix} X \\ Y \\ Z \\ 1 \\ \end{pmatrix} \to \begin{pmatrix} fX + Zp_x\\ fY + Zp_y \\ Z \\ \end{pmatrix} &= \begin{bmatrix} f & & p_x & 0 \\ & f & p_y & 0\\ & & 1 & 0 \\ \end{bmatrix} \begin{pmatrix} X \\ Y \\ Z \\ 1 \\ \end{pmatrix} \\ &= \begin{bmatrix} f & & p_x \\ & f & p_y\\ & & 1 \\ \end{bmatrix} \begin{bmatrix} 1 & & & 0 \\ & 1 & & 0\\ & & 1 &0 \\ \end{bmatrix} \begin{pmatrix} X \\ Y \\ Z \\ 1 \\ \end{pmatrix} \end{align*}
◦
px,pyp_x, p_y 는 중심점으로부터 Priniciple Point 까지의 보정에 필요한 offset 을 의미함.
◦
Intrinsic Parameter (K)(K) 에 px,pyp_x,p_y 항목이 추가됨.
•
3D Coordinate 의 측정 physical unit 을 pixel unit 으로 바꾸기 위해 다음과 같은 보정을 할 수 있음.
K=[fpxfpy1]→K=[αxx0αyy01]K= \begin{bmatrix} f & & p_x \\ & f & p_y \\ & & 1 \end{bmatrix} \to K= \begin{bmatrix} \alpha_x & & x_0 \\ & \alpha_y & y_0 \\ & & 1 \end{bmatrix}
◦
αx=mxf,αy=myf\alpha_x = m_xf, \alpha_y = m_yf
◦
mx,mym_x, m_y 는 physical pixel 을 pixel unit 으로 바꾸기 위한 scaling factor 임.
◦
x,yx, y 방향의 scaling factor 가 다른 것은 non-squared pixels 를 다루는 경우를 일반화 한 것임.
•
더 일반적으로는, pixel 이 perpendicular 하지 않은 경우 (e.g. 평행사변형 픽셀) 를 대응하기 위해 Skew Parameter ss 를 도입해 다음과 같이 Intrinsic Parameter 를 구축할 수 있음
K=[αxx0αyy01]→K=[αxsx0αyy01]K=\begin{bmatrix} \alpha_x & & x_0 \\ & \alpha_y & y_0 \\ & & 1 \end{bmatrix} \to K = \begin{bmatrix} \alpha_x & s& x_0 \\ & \alpha_y & y_0 \\ & & 1 \end{bmatrix}

Focal Length

•
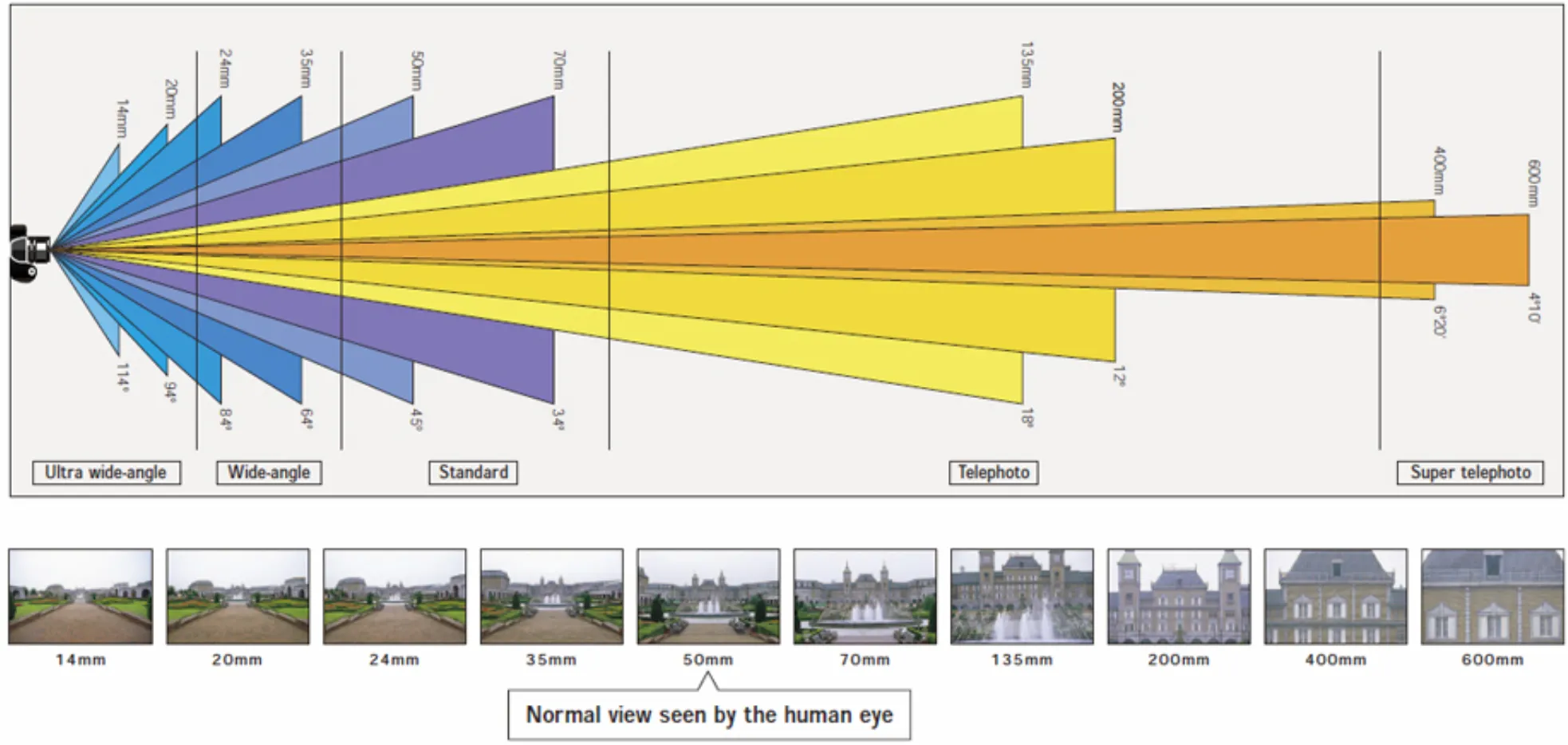
낮은 focal length 를 가지면 wide view 를 가지고 있지만, 확대의 비율이 적음.
◦
동일한 크기의 Image Plane 을 가정했을 때 볼 수 있는 범위가 넓음.
•
높은 focal length 를 가지면 narrow view 를 가지고 있지만, 확대의 비율이 큼.
◦
동일한 크기의 Image Plane 을 가정했을 때 볼 수 있는 범위가 좁음.

Extrinsic Parameters

•
간단한 상황에서는 Camera Center 를 (0,0,0)(0,0,0) 으로 가정했지만, 실제에서는 그렇지 않음.
•
World Coordinate 를 Camer Coordinate 로 변환하는 과정이 Extrinsic Parameter 에 의해 진행됨.
•
이러한 좌표계 변환은 rotation matrix RR 과 translation t{\rm t} 에 의해 다음과 같이 나타낼 수 있음.
Xcam=RXworld+t=[R∣t][Xworld1]{\rm X}_{\rm cam} = R{\rm X_{world}} + {\rm t} = \begin{bmatrix} R | {\rm t} \end{bmatrix} \begin{bmatrix} {\rm X_{world}} \\ 1 \end{bmatrix}
•
위 변환을 이용해 기존의 변환된 Camera Center 가 (0,0,0)T(0,0,0)^T 이 되도록 하기 위해 다음과 같은 식을 세울 수 있음.
Ccam=(0,0,0)T=RCworld+t−RCworld=tCworld=−RTt{\rm C_{cam}} = (0,0,0)^T = R{\rm C_{world}} + {\rm t} \\ -R{\rm C_{world}} = {\rm t} \\ {\rm C_{world}} = -R^T{\rm t}
◦
이 식을 활용해 R,tR, {\rm t} 를 구할 수 있음.
•
최종적으로는 World Coordinate 를 Camera Coordinate 로 변환한 뒤에 Intrinsic Parameter 를 적용해 Camera System 을 구축함.
x=PXworld=K[R∣t]Xworld{\rm x} = {\rm PX_{world}} = K[R|{ \rm t}]{\rm X_{world}}
•
Camera Calibration 은 K,R,tK,R,{\rm t} 를 구하는 과정임.

Finite Projective Cameras

P=K[R∣t]=KR[I∣−Cworld]{\rm P} = K[R | {\rm t}] = KR[I | -{\rm C_{world}}]
•
PP 는 총 11DoF
◦
KK 는 5DoF: αx,αy,s,x0,y0\alpha_x, \alpha_y, s, x_0, y_0
◦
RR 은 3DoF: Roll, Pitch, Yaw
◦
t{\rm t} 는 3DoF: tx,ty,tzt_x, t_y, t_z
•
Finite Projective Camera 는 다음과 같이 정의됨.
◦
모든 좌측 3×33\times3 이 Non-Singular 인 3×43\times 4 matrix 는 Projective Camera 의 Camera Matrix 가 될 수 있음.
•
Cworld{\rm C_{world}} 의 projection 인 Ccam{\rm C_{cam}} 은 의도대로 (0,0,0)T(0,0,0)^T 임.